物理の入試問題を解く

トップページ ＞ 熱と気体 ＞ p-Vグラフ　Ⅱ

 

・モル比熱\(C\)［\(J/\left(mol\cdot K\right)\)］とは、物質1molの温度を1K高めるのに必要な熱量のことを言います。
　 物質\(n[mol]\)を\(\Delta T\)だけ温度を高めるのに必要な熱量\(Q\)は、次のように表されます。
\begin{equation} Q=nC\Delta T \tag{3-1} \end{equation}
　\(C\)の値は、状態がどのように変化するか（定積変化、定圧変化、その他の状態変化）により異なります。

 

・等温変化：絶対温度と内部エネルギーは変化しません。
　　　　　　　熱力学第一法則から、[気体が吸収する熱量]=0+[気体が外部にした仕事]
　　　　　　　⇒吸収した熱量で外部に仕事をします。
・断熱変化：気体に熱量の出入りはありません。
　　　　　　　熱力学第一法則から、0＝[気体の内部エネルギーの変化量]+[気体が外部にした仕事]
　　　　　　　⇒内部エネルギーの一部を使って外部に仕事をします。
　　　　　　　⇒外部に仕事をすると、冷えます。　
　　　　　　　⇒外部から仕事をされると、温まります。

 

・熱機関の効率（熱効率）の式
\begin{eqnarray}
e&=&\frac{W}{Q_{in}} \tag{3-20} \\
e&=&\frac{Q_{in}-Q_{out}}{Q_{in}} \tag{3-22} \\
ただし、e&:&熱効率 \\
W&:&熱機関がした仕事 \\
Q_{in}&:&（高温の物体から）吸収した熱量（\gt 0） \\
Q_{out}&:&（低温の物体に）放出した熱量、捨てた熱量（\gt 0)）
\end{eqnarray} 　

 

・ｐ-Vグラフ関連の問題の解き方
　最初に、状態変化の様子を見極めます。
　⇒変化しないものは何か・・・[圧力]か、[体積]か、[絶対温度]か
　⇒\(0\)であるものは何か・・・[気体が吸収する熱量]か、[内部エネルギーの変化量]か、[気体が外部にする仕事]か

 

　使う基本の式は、「状態方程式」と「熱力学第一法則」、
　　　　　　　「内部エネルギーの変化量を表す式」と「気体が外部にする仕事を計算する式」です。

 

 

 

１．定積モル比熱と定圧モル比熱

 

　比熱についてまとめると、次のようになります。

 

 

 

 

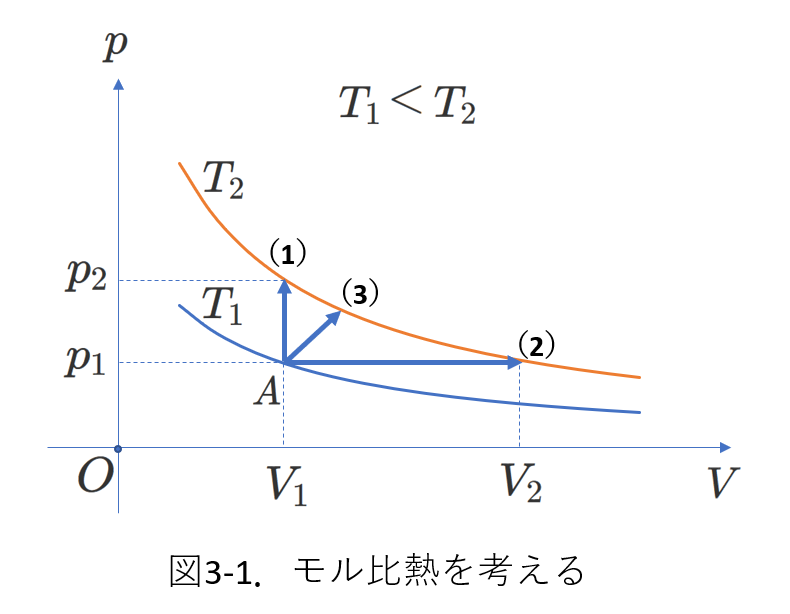
　右図3-1を用いて、比熱について考えます。

 

　絶対温度\(T_1\)と\(T_2\)の2本の等温線が描かれています。

 

　\(n\)モルの物質が、温度\(T_1\)上の状態\(A\)から絶対温度\(T_2\)の状態に変化することを考えます。
図には、3つの過程が描かれています。（1）（2）（3）の3つです。

 

　さて、モル比熱とは、物質1molの温度を1K高めるのに必要な熱量のことを言います。
必要な熱量は、どんな変化をするか（どんな過程を通るか）で、異なります。
\(T_1\)の物質を\(T_2\)まで温度を高めるのですが、必要な熱量は、\(A\to (1)\)と\(A\to (2)\)と\(A\to (3)\)で、異なります。なので、モル比熱も異なります。

 

　それぞれの変化における、熱力学の第一法則を考えると、
\begin{equation} Q=\Delta U+W \tag{3-7} \end{equation}
\(Q\)は気体が吸収する熱量、\(\Delta U\)は内部エネルギーの変化量、\(W\)は気体が外部にした仕事です。

 

　　モル比熱\(C\)は、物質1molの温度を1K高めるのに必要な熱量ですから、（3-1）式と（3-6）式から、
\begin{equation} C=\frac{Q}{n(T_2-T_1)}=\frac{\Delta U}{n(T_2-T_1)}+\frac{W}{n(T_2-T_1)} \tag{3-8} \end{equation}
となります。

 

　\(A\to (1)\)の変化は、定積変化ですから、外部に仕事をしません。
つまり、（3-8）式において、\(W=0\)です。
これより、定積モル比熱\(C_V\)を計算できます。さらに、単原子分子理想気体を考えれば、（2-3）式\(\Delta U=\frac{3}{2}nR\Delta T\)を適用できて、
\begin{eqnarray} C_V&=&\frac{\Delta U}{n(T_2-T_1)} \\
&=&\frac{\frac{3}{2}nR(T_2-T_1)}{n(T_2-T_1)}=\frac{3}{2}R \tag{3-9} \end{eqnarray}
となります。

 

　次に、過程\(A\to (2)\)は定圧変化です。
このときは、気体は外部に仕事をします。

 

　図3-1から,\(W=p_1(V_2-V_1)=p_1V_2-p_1V_1\)です。
また、状態方程式を用いれば、\(p_1V_1=nRT_1\)、\(p_1V_2=nRT_2\)です。

 

　これらと、再び単原子分子理想気体を想定して、（2-3）式を適用すれば、定圧モル比熱\(C_p\)は、
\begin{eqnarray} C_p&=&\frac{\frac{3}{2}nR(T_2-T_1)}{n(T_2-T_1)}+\frac{p_1V_2-p_1V_1}{n(T_2-T_1)} \\
&=&C_V+\frac{nRT_2-nRT_1}{n(T_2-T_1)}=C_V+R \tag{3-10} \\
&=&\frac{3}{2}R+R=\frac{5}{2}R \tag{3-11}
\end{eqnarray}
　ここで、(3-10)式は、単原子分子理想気体について、マイヤーの関係が成り立つことを証明する式になっています。

 

 

　

 

例題

　図3-2において、nモルの単原子分子理想気体の状態が\(A\)から\(B\)に直線的に変化するときのモル比熱を求めます。

 

　モル比熱とは、物質1molの温度を1K高めるのに必要な熱量のことを言いますから、変化に伴って気体が吸収した熱量\(Q_{in}\)を求めればよいです。
そして、その熱量を1モル当たりと1K当たりに換算するために、求めた熱量\(Q_{in}\)をモル数\(n\)と、温度変化\(\Delta T\)で割ります。
\(\Delta T\)を求めるために、状態\(A\)と\(B\)の絶対温度を求めます。

 

　状態\(A\)、\(B\)の絶対温度をそれぞれ\(T_A\)、\(T_B\)として、ふたつの状態について状態方程式から絶対温度を求めます。
\begin{eqnarray} Aについて、　2p_0\cdot V_0&=&nRT_A \\
T_A&=&\frac{2p_0 V_0}{nR} \tag{3-12} \\
Bについて、　p_0\cdot 3V_0&=&nRT_B \\
T_B&=&\frac{3p_0 V_0}{nR} \tag{3-13} \\
\Delta T&=&T_B-T_A=\frac{p_0 V_0}{nR} \tag{3-14}
\end{eqnarray}

 

　次に、\(Q_{in}\)を求めます。
内部エネルギーの変化は、（3-14）)式の\(\Delta T\)から求められます。
また、気体は膨張していますから、気体は外部に仕事をしていて、その大きさ\(W_{out}\)は線分\(AB\)と\(V\)軸の間の面積で与えられます。
以上より、
\begin{eqnarray} Q_{in}&=&\Delta U+W_{out} \\
&=&\frac{3}{2}nR\Delta T+W_{out}=\frac{3}{2}nR\frac{p_0 V_0}{nR}+\frac{1}{2}(2p_0+p_0)(3V_0-V_0) \\
&=&\frac{3}{2}p_0 V_0+3p_0 V_0=\frac{9}{2}p_0 V_0 \tag{3-15}
\end{eqnarray}

 

　これより、モル比熱\(C\)は、
\begin{equation} C=\frac{Q_{in}}{n\Delta T}=\frac{\frac{9}{2}p_0 V_0}{n\frac{p_0 V_0}{nR}}=\frac{9}{2}R \tag{3-16} \end{equation}
となります。
　定積モル比熱や定圧モル比熱は知っていても、「モル比熱とは、物質1molの温度を1K高めるのに必要な熱量のこと」を理解していないとこの問題は解けないですね。

 

 

 

２．断熱変化と等温変化を比較する

 

 

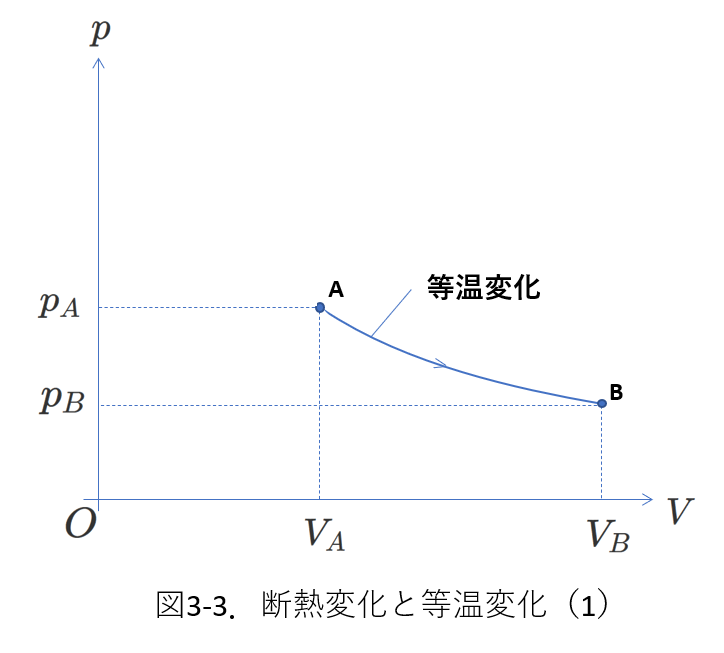
　図3-3は、\(n\)モルの単原子分子理想気体が状態\(A\)から状態\(B\)に等温変化する場合の\(p-V\)グラフです。
同じ状態\(A\)から断熱変化で、状態\(B\)と同じ体積\(V_B\)になった状態を\(C\)とします。
状態\(C\)の圧力\(p_C\)が\(p_B\)より大きいのか、同じなのか、小さいのかを、熱力学第一法則から考えます。

 

　熱力学第一法則は、次の通りです。
\begin{eqnarray} Q_{in}&=&\Delta U+W_{out} \tag{3-17} \\
Q_{in}&:&気体が吸収する熱量　　\\
\Delta U&:&内部エネルギーの変化量 \\
W_{out}&:&気体が外部にした仕事
\end{eqnarray}

 

　等温変化では、温度は変化しないので、内部エネルギーの変化量\(\Delta U=0\)です。
　図3-3の等温変化では体積が増加していますから、気体は外部に仕事\(W_{out}（\gt 0）\)をしていることになります。
（3-17）式から、気体は、外部にした仕事\(W_{out}\)に等しい熱量を、吸収することになります。

 

　一方、断熱変化では、気体への熱量の出入りはなし、つまり、\(Q_{in}=0\)です。
そして、体積は増加するので、気体は外部に対して仕事をします。
この仕事を\(W'_{out}\)とすれば、\(W'_{out}\gt 0\)です。
　（\(W'_{out}\)と\(W_{out}\)の大きさの比較はここでは示しませんが、後ほどわかるように、\(W'_{out}\lt W_{out}\)です。）
　(3-17)式から、
\begin{eqnarray} 0=\Delta U+W'_{out} \tag{3-18} \\
これより、\Delta U=-W'_{out} \lt 0 \tag{3-19}
\end{eqnarray}

　(3-19)式から内部エネルギーが負ということは、絶対温度が下がることを意味します。
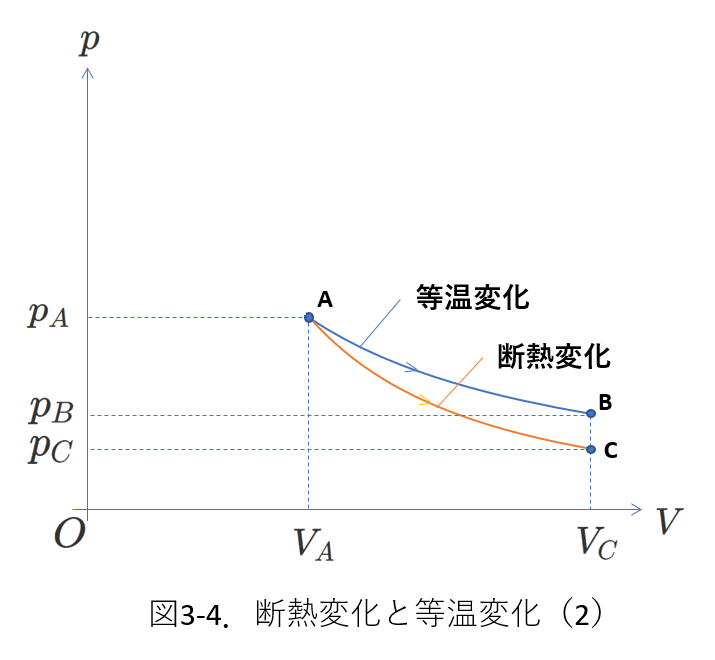
したがって、同じ体積に変化する場合、状態\(C\)は状態\(B\)よりも、\(pV\)グラフで下（すなわち、\(p_C \lt p_B\)となります。

 

 

 

　断熱変化の状態をグラフに表すと図3-4となります。

 

 

 

 

 

 

 

 

 

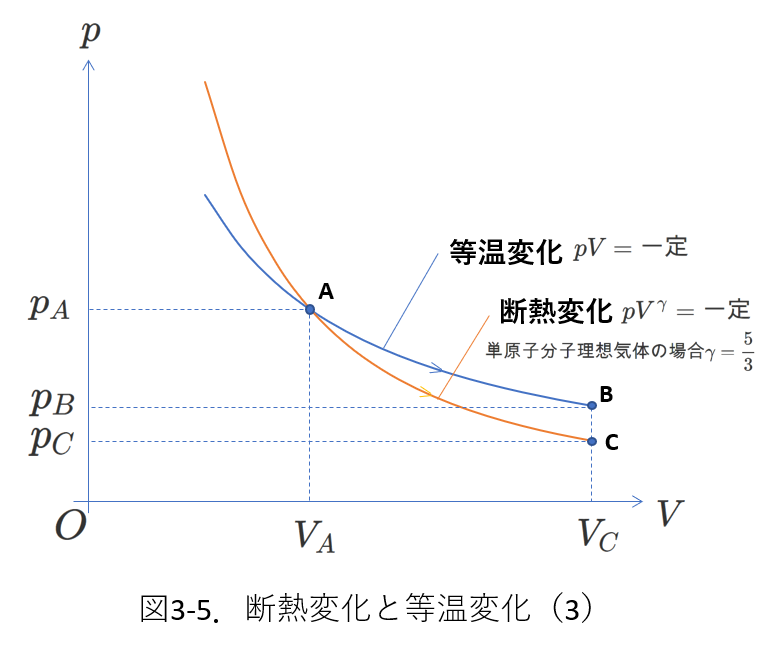
　断熱変化では（3-6）式「\(PV^{\gamma} =一定\)」がなりたちます。
この式にしたがってグラフを描くと図3-5のようになります。
　図3-5では、状態\(A\)の左側（体積の小さい側）も示しました。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

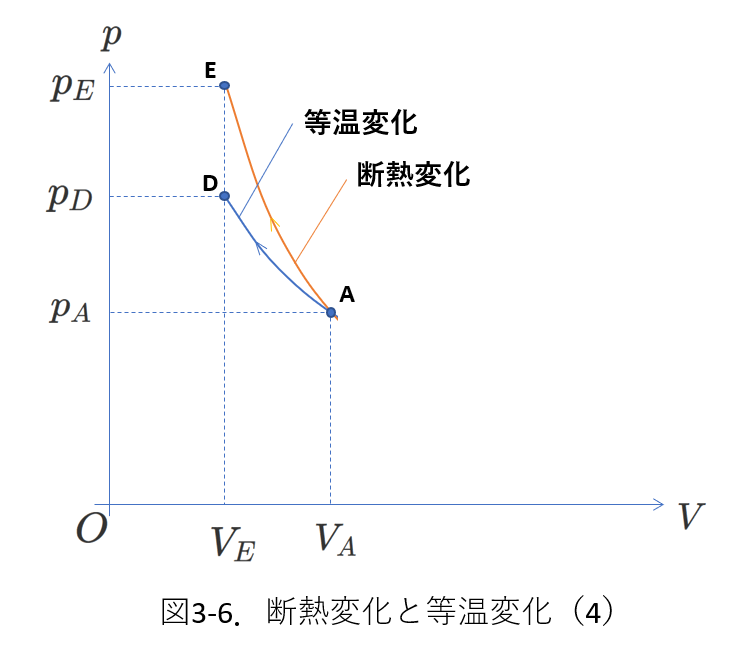
　図3-6では、気体が状態\(A\)から等温変化や断熱変化で体積が\(V_E\)に変化する過程を描いています。
このとき、断熱変化のほうが図のうえで上（つまり絶対温度が高い側）になります。

 

　この理由を考えます。
　断熱変化の場合、\(Q_{in}=0\)です。
また、このとき気体が外部にする仕事を\(W"_{out}\)とすると、気体の体積が減少しているわけですから、\(W"_{out}\lt 0\)です。

 

　以上を熱力学第一法則に適用すると、
\begin{eqnarray} 0&=&\Delta U"+W"_{out} \\
\Delta U"&=&-W"_{out}\gt 0
\end{eqnarray}
　気体の内部エネルギーの変化量\(\Delta U"\)は正となりますから、絶対温度は増加、したがって、断熱変化のグラフは等温変化のグラフより上になります。
　\(W"_{out}\lt 0\)は気体が仕事をされたことを意味していますから、熱量の出入りがなければ、仕事された分、絶対温度が増加します。

 

 

 

 

 

３．各変化における、\(Q、\Delta U、W\)の正負を考える

 

　\(p-V\)グラフを使った問題では、ある変化における[気体に流入する熱量：\(Q_{in}\)]、[気体の内部エネルギーの変化量：\(\Delta U\)]［気体が外部にした仕事：\(W_{out}\)]を求めることがあります。
　このとき諸量の正負を間違えることが多いです。

 

　正しい式で、\(Q_{in}\)、\(\Delta U\)、\(W_{out}\)を計算すれば、符号も正しいものが得られますから、正しい式を立てるのが大事です。
　しかし、引き算の順序を間違えるなどで、うっかり符号をミスすることはあります。
そのようなミスを防ぐ意味でも、また、そのようなミスを発見する上でも、式とは別に符号の正負を確認しておくのは良いことです。

 

　そこで、ここでは、様々な状態変化について、\(Q_{in}\)、\(\Delta U\)、\(W_{out}\)の正負を考えます。

 

 

 

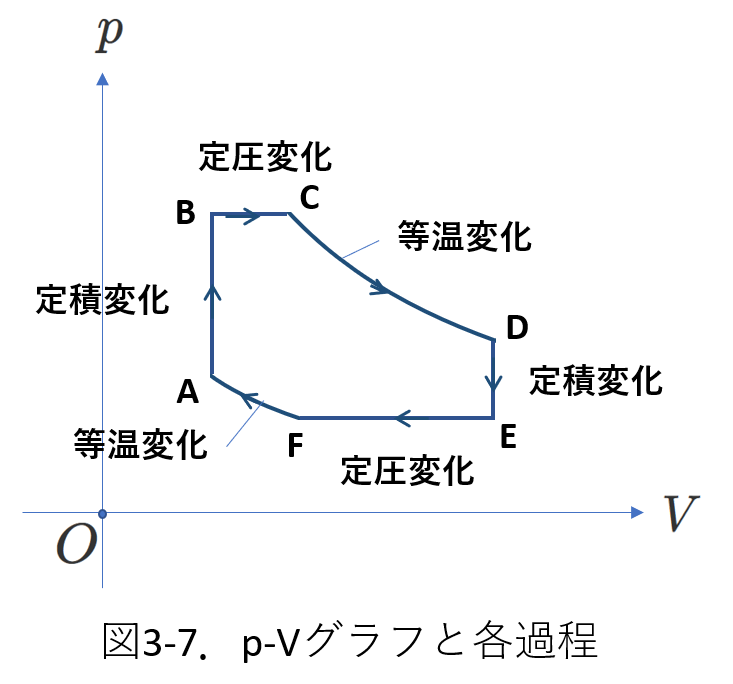
　図3-7に表した6つの状態変化について考えます。

 

　各状態変化で、考えるべきことを説明します。
　\(W_{out}\)：仕事の正負は体積の変化から考えます。膨張していれば、気体は外部に仕事をしているわけで\(W_{out}\gt 0\)、体積が一定（定積変化）ならば\(W_{out}=0\)、体積が減少（収縮）しているならば、\(W_{out}\lt 0\)です。

 

　\(\Delta U\)：単原子分子理想気体の場合は\(\Delta U=\frac{3}{2}nR\Delta T\)ですから、温度変化から正負を判断できます。つまり、温度が上昇すれば\(\Delta U\gt 0\)、温度が一定（等温変化）の場合\(\Delta U=0\)、温度が下降する場合は\(\Delta U\lt 0\)です。

 

　\(Q_{in}\)：断熱変化の場合は\(Q_{in}=0\)です。それ以外の場合には、熱力学第一法則の式\(Q_{in}=\Delta U+W_{out}\)から\(Q_{in}\)の正負を判断することになります。

 

 

　さて、下の表に、図3-7の6つの変化について諸量の正負の考え方をまとめました。

 

　最初の\(A\to B\)の定積変化を例にして、この表の見方を説明します。

 

　\(A\to B\)の欄を右にたどって、最初に記入されている欄の\(W_{out}\)の正負を最初に考えます。
この変化は定積変化で体積は一定ですから、\(W_{out}=0\)です。

 

　さらに右にたどって、次に\(\Delta U\)の正負を考えます。
図1-5を思い返せば、この過程で絶対温度は増加することがわかります。
つまり、\(\Delta U\)は正です。

 

　次は、\(Q_{in}\)ですが、これは表に示したように、熱力学の第一法則から正であることがわかります。

 

　ほかの過程においても、行を右にたどって、記入された欄の順序どおりに考えを進めるとよいです。
常に左のものから右にたどって考えを進めれば良いように、\(Q_{in}\)などの列を2つ設けました。
　もっとも、\(A\to B\)の過程では、最初に\(\Delta U\)を、次に\(W_{out}\)を考えても良いです。

 

変化	\(Q_{in}\)	\(\Delta U\)	\(W_{out}\)	\(Q_{in}\)	\(\Delta U\)	\(Q_{in}\)
\(A\to B\) 定積変化			定積なので、0		温度は上昇する ので、正	\(Q_{in}=\Delta U\) より、正
\(B\to C\) 定圧変化			体積は増加する ので、正		温度は上昇する ので、正	\(Q_{in}=\Delta U+W_{out}\) より、正
\(C\to D\) 等温変化		等温なので、0	体積は増加する ので、正	\(Q_{in}=W_{out}\) より、正
\(D\to E\) 定積変化			定積なので、0		温度は減少する ので、負	\(Q_{in}=\Delta U\) より、負
\(E\to F\) 定圧変化			体積は減少する ので、負		温度は減少する ので、負	\(Q_{in}=\Delta U+W_{out}\) より、負
\(F\to A\) 等温変化		等温なので、0	体積は減少する ので、負	\(Q_{in}=W_{out}\) より、負
\(C\to D\) 断熱変化	断熱なので、0		体積は増加する ので、正		\(\Delta U=-W_{out}\)なので、負
\(F\to A\) 断熱変化	断熱なので、0		体積は減少する ので、負		\(\Delta U=-W_{out}\)なので、正

 

　最後の2行では断熱変化について考えています。
　図3-7で等温変化であった\(C\to D\)と\(F\to A\)が断熱変化の場合の諸量の正負を説明しました。

 

　

 

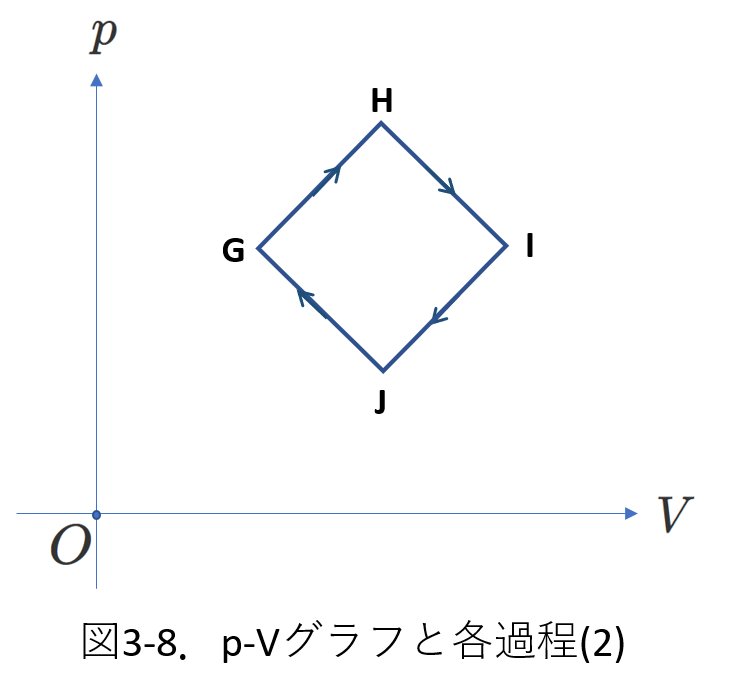
　たいへん特殊な例ですが、図3-8のような4つの変化を考えて、下の表にまとめました。
　どの変化も、一定である量がありませんが、\(G\to H\)と\(I\to J\)の過程については、\(p-V\)グラフから、それぞれの正負を知ることができます。　　

 

変化	\(Q_{in}\)	\(\Delta U\)	\(W_{out}\)	\(Q_{in}\)	\(\Delta U\)	\(Q_{in}\)
\(G\to H\)			体積は増加する ので、正		温度は上昇するので、正	\(Q_{in}=\Delta U+W_{out}\)より、正
\(H\to I\)			体積は増加する ので、正		不明	不明
\(I\to J\)			体積は減少する ので、負		温度は減少するので、負	\(Q_{in}=\Delta U+W_{out}\)より、負
\(J\to G\)			体積は減少する ので、負		不明	不明

 

 

 

 

 

４．熱機関の効率

 

　蒸気機関のように、熱の吸収と放出を繰り返して、熱を仕事に変換する装置を、熱機関と呼びます。

 

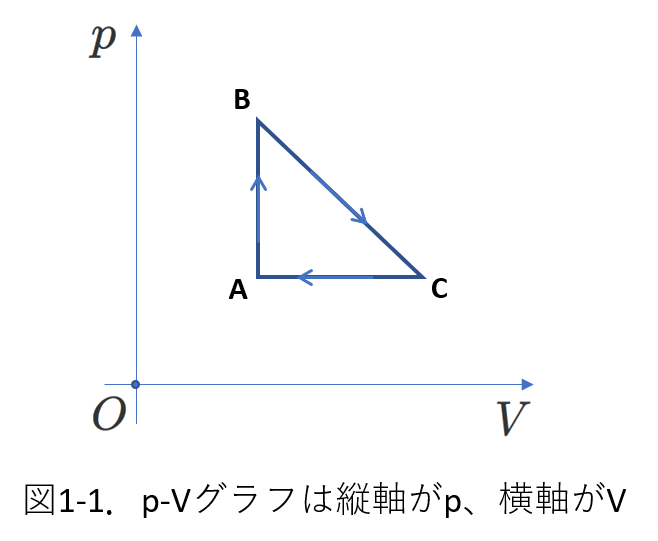
　右の図1-1のように、気体の状態が、状態Aから始まって、\(A\to B\to C\to A\)ともとの状態\(A\)に戻ってくるとき、この一連の状態変化をサイクルと呼びます。
これは、熱機関のモデルとして考えることができます。

 

　ここでは、熱機関の効率について考えます。
「効率」は、「入力」のどのぐらいの部分が、目的の「出力」に変換できたかどうかを表します。
簡単に表現すれば、「出力」/「入力」です。
　そして、スタートから1サイクルの間で効率を考えます。
　1サイクルという意味は、1サイクルの途中で効率を考えたりしないということです。

 

　さて、熱機関の効率は、次のように表されます。
\begin{eqnarray}
[熱機関の効率]&=&\frac{[熱機関がした仕事]}{[熱機関が吸収した熱量]}　 \tag{3-20} 　\\
[熱機関の効率]&=&\frac{[熱機関が外部にした仕事]-[熱機関が外部からされた仕事]}{[熱機関が吸収した熱量]}　 \tag{3-21} 　\\
e&=&\frac{W}{Q_{in}} \tag{3-20} \\
e&=&\frac{Q_{in}-Q_{out}}{Q_{in}} \tag{3-22} \\
ただし、e&:&熱効率 \\
W&:&熱機関がした仕事 \\
Q_{in}&:&（高温の物体から）吸収した熱量（\gt 0)） \\
Q_{out}&:&（低温の物体に）放出した熱量、捨てた熱量（\gt 0)）
\end{eqnarray} 　

 

 

　[熱効率]は、[出力]と[入力]の比を考えるのですが、比の「分子」「分母」に何が含まれるかを明確に覚える必要があります。

 

　「分母」に入るのは、1サイクルの間に熱機関が（高温の物体から）吸収した熱量\(Q_{in}(\gt 0)\)です。
[放出した熱量]も負号をつけて、[吸収した仕事]と表すことがありますが、ここでは、そういうものを含めません。
1サイクルの各過程で、[吸収した熱量]（>0）を求めて合計したものを「分母」に入れます。

 

　一方で、「分子」は「熱機関が(外部）にした仕事ですが、[した仕事](>0)から[された仕事](>0)を引いて求めます。
言い変えれば、1サイクルの中で[した仕事]を正負も含めて求めて、その和を「分子」に入れます。

 

　説明がごちゃごちゃしていますが、要は負の項目も数えるかどうかです。
「分母」の[吸収した熱量]については、正の項目だけ、「分子」の仕事については、正負両方を考えるわけです。
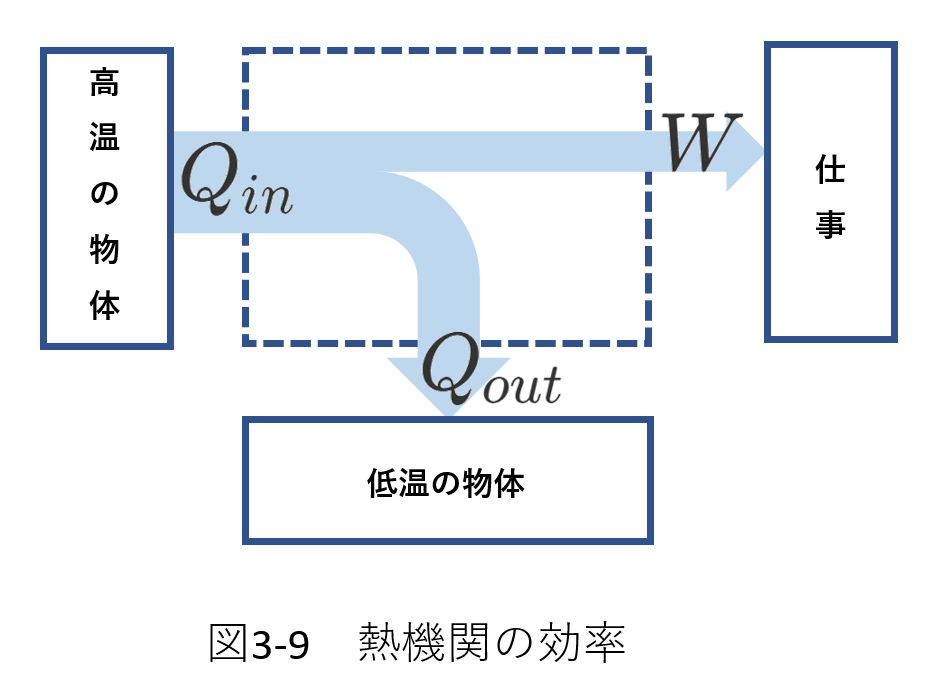
図3-9を思い浮かべると、[熱機関の効率]が理解しやすくなると思います。
　さらに、この図から、\(0\lt e\lt 1\) であることもわかります。
求めた熱効率\(e\)が、\(e=1\) や\(e\gt 1\) となったら、どこかでミスをしたと考えましょう。

 

　熱機関が低温の物体に触れることで放出する熱量は、再利用することができません。
低温の物体から高温の物体に熱量を移動する方法がないからです。
熱機関が放出した熱量は、吸収してみたけれど、使われず捨てることになった熱量です。

 

　さて、（3-20）式と（3-22）式を考えます。
　1サイクルを経て元の状態に戻るということは、1サイクルを経て始めの絶対温度に戻ることになるわけですから、1サイクル後には内部エネルギーの変化は\(0\)となります。
熱力学の第一法則を適用すると、
\begin{eqnarray} Q_{in}-Q_{out}&=&\Delta U+W \\
&=&W
\end{eqnarray}
つまり、\(W=Q_{in}-Q_{out}\)ですから、（3-20）式は（3-22）式に変換できます。

 

　（3-22）式も強力な公式ですから、覚えておきましょう。
　この式のほうが、理解しやすいかもしれません。
\(Q_{in}\)のうち\(Q_{out}\)が使われずに捨てられます。
\(Q_{in}\)のうち、\(Q_{in}-Q_{out}\)が使われるので、熱効率が(3-22)式で表されるわけです。

 

 

 

　では、具体的な場合について「熱機関の効率」を考えます。

 

例題1）

 

　最初の例題は、図3-10です。

 

　状態\(A\)から\(B\to C\to D\to A\)が1サイクルです。
この熱機関のモデルの熱効率を求めます。　気体は単原子分子理想気体で考えます。

 

　熱効率を求めるには、[吸収した熱量]と[仕事]を求める必要があります。

 

まず、[仕事]について考えます。
\(A\to B\)は、定積変化(過程）で仕事は\(0\)
\(B\to C\)は、定圧変化（過程）で、体積が増加していますから、外部に\(W_{BC}\)の仕事をします。
その大きさは、辺BCとV軸に囲まれた面積に相当します。

 

\(C\to D\)は、定積変化(過程）で仕事は\(0\)
\(D\to A\)は、定圧変化で、体積が減少していますから、外部から\(W_{DA}（\gt 0）\)の仕事をされます。
（または、外部に\(-W_{DA}\)の仕事をすると、表現できます。）

 

　以上の内容から、[熱機関の熱効率]の「分子」に当たる物は、\(W_{BC}-W_{DA}\)です。
これは、四角形\(ABCD\)の面積に相当します。

 

　では、[熱効率]の「分母」は・・・
\(A\to B\)は、定積変化(過程）で仕事は\(0\)、熱力学の第一法則から、\(Q_{in}=[\)内部エネルギーの変化量：\(\Delta U_{AB}\)]で、これは圧力と体積から計算できます。
\(B\to C\)は、定圧変化（過程）で、\(Q_{in}\)は定圧モル比熱からすぐに計算できます。
（普通\(Q_{in}\)を計算するときには、内部エネルギーの変化量と仕事の両方を計算しますが、定圧変化では定圧モル比熱を使えばただちに\(Q_{in}\)が求まります。　ただし、この計算をすると、外部に仕事をしていることを忘れてしまうことがあるので、注意が必要です。）
\(C\to D\)と\(D\to A\)も同様に計算できます。

 

 

　各過程ごとに、[内部エネルギーの変化量]、[外部にした仕事]を計算して、次のように表に示します。

 

過程		内部エネルギー変化 \(\Delta U=\frac{3}{2}\Delta (pV)\)	外部にした仕事 \(W_{out}\)	気体が吸収した熱量 \(Q=\Delta U+W_{out}\)
\(A\to B\)	定積	\(\frac{3}{2}(p_2V_1-p_1V_1) \\ =\frac{3}{2}V_1(p_2-p_1)\)	\(0\)	\(\frac{3}{2}V_1(p_2-p_1) \gt 0 \)
\(B\to C\)	定圧	\(\frac{3}{2}(p_2V_2-p_2V_1) \\ =\frac{3}{2}p_2(V_2-V_1)\)	\(p_2(V_2-V_1)\)	\(\frac{3}{2}p_2(V_2-V_1)+p_2(V_2-V_1) \\ =\frac{5}{2}p_2(V_2-V_1) \gt 0\)
\(C\to D\)	定積	\(\frac{3}{2}(p_1V_2-p_2V_2) \\ =\frac{3}{2}V_2(p_1-p_2)\)	\(0\)	\(\frac{3}{2}V_2(p_1-p_2) \lt 0 \)
\(D\to A\)	定圧	\(\frac{3}{2}(p_1V_1-p_1V_2) \\ =\frac{3}{2}p_1(V_1-V_2)\)	\(p_1(V_1-V_2) \\ =-p_1(V_2-V_1)\)	\(\frac{3}{2}p_1(V_1-V_2)+p_1(V_2-V_1) \\ =-\frac{5}{2}p_1(V_2-V_1) \lt 0\)
1サイクル		\(0\)	\((p_2-p_1)(V_2-V_1)\)	\(\frac{3}{2}(V_1-V_2)(p_2-p_1)+\frac{5}{2}(p_2-p_1)(V_2-V_1)\) \(=(p_2-p_1)(V_2-V_1)\)

 

　このような表を作ると、わかりやすく、ミスを起こしにくいです。
　この表の項目には、「仕事」は「した仕事」なのか「された仕事」なのか、「熱量」は「吸収した熱量」なのか「放出した熱量」なのか、を明記しておくと、さらにミスを減らせます。

 

　内部エネルギー変化量の\(\Delta (pV)\)は、\(pV\)の積の変化量を表しています。
状態\(A\)から\(B\)の変化であれば、\(\Delta (pV)=p_BV_B-p_AV_A\)です。
[変化量]=[変化後の量]-[変化前の量]であることも再確認しておきましょう。
外部にした仕事\(W_{out}=p\Delta V\)と表されます。
[仕事]の大きさは\(pV\)グラフ上の面積で表されますが、\(\Delta V=[変化後の体積]-[変化前の体積]\)として計算すれば、正負も含めて\(W_{out}\)が求められます。

 

　表中には、変化の過程、「定積」「定圧」「等温」「断熱」なども記すとよいです。

 

　そして、最初に\(0\)を表中に書き入れます。
定積過程の場合の\(W_{out}\)、「等温」の[内部エネルギーの変化]、「断熱」の[吸収した熱量]が\(0\)となります。

 

　さて、表の中身を検討します。
①　1サイクルの[内部エネルギー変化]（\(A\to B\to C\to D\to A\)の各過程での[内部エネルギーの変化]の和)は、\(0\)になっています。
1サイクルで同じ状態（同じ絶対温度）に戻るわけですから、[内部エネルギーの変化量]は\(0\)になりますね。

 

②　ついで、1サイクルでの\(W_{out}\)の合計が\((p_2-p_1)(V_2-V_1)\)は、図3-10の\(p-V\)グラフの四角形\(ABCD\)の面積になっています。

 

③　そして、[気体が吸収した熱量]\(Q\)の1サイクルの合計は、1サイクルの\(W_{out}\)に等しいことも確認できます。
　（図3-9が示すことと一致しています。）

 

　①と③は、上表を作った時の検算として使えます。

 

　さて、[熱機関の熱効率]を求めます。
各過程の\(Q\)の内、正の値であるのは、\(A\to B\)と\(B\to C\)です。
これらの和が、[熱効率]の分母です。
誤って、1サイクルの\(Q\)の合計で計算しないようにしましょう。

 

(3-20）式を使っても、（3-22）式を使っても、熱効率\(e\)は、
\begin{eqnarray} e&=&\frac{(p_2-p_1)(V_2-V_1)}{\frac{3}{2}V_1(p_2-p_1)+\frac{5}{2}p_2(V_2-V_1)} \\
&=&\frac{2(p_2-p_1)(V_2-V_1)}{5p_2V_2-3p_1V_1-2p_2V_1}
\end{eqnarray}

 

 

 

例題2　カルノーサイクル

 

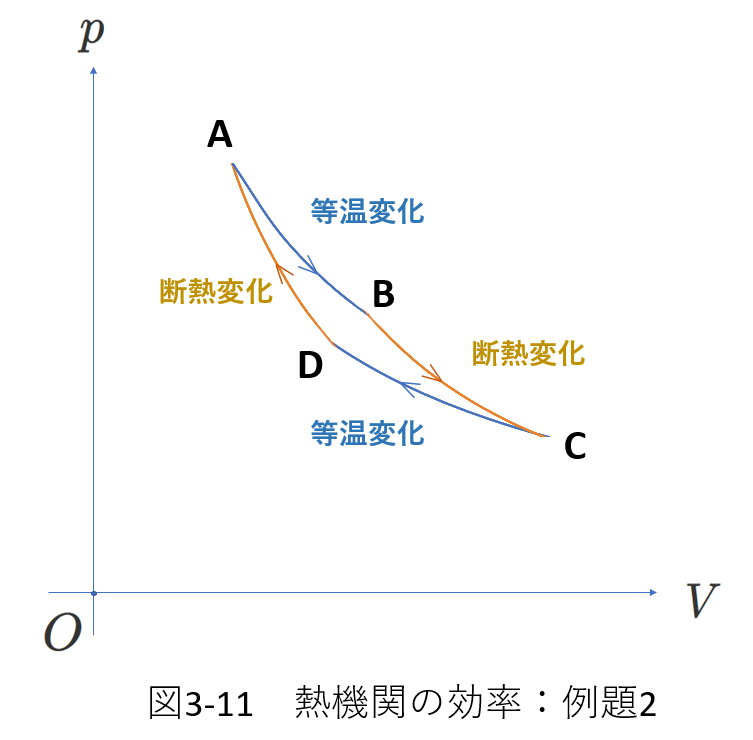
　次の例を、図3-11に示します。

 

　例題1は定積変化と定圧変化の組み合わせでしたが、例題2は等温変化と断熱変化の組み合わせです。

 

　\(A\to B\)：等温膨張
　\(B\to C\)：断熱膨張
　\(C\to D\)：等温収縮
　\(D\to A\)：断熱収縮
です。

 

　等温変化では内部エネルギーの変化量は\(0\)です。
\(A\to B\)では、体積が増加しています。
つまり、外部に仕事をしていますが、その分の熱量を気体は吸収します。
この熱量を\(Q_1\)とします。
一方、\(C\to D\)では、体積が減少しています。その分の熱量を、気体は放出しています。
この熱量を\(Q_2\)とします。

 

　この熱機関の熱効率を\(Q_1\)と\(Q_2\)で表すのが問題です。

 

　\(B\to C\)と\(D\to A\)は断熱変化ですから、気体が吸収する熱量は\(0\)です。
したがって、熱機関が吸収する熱は\(Q_1\)、放出する熱は\(Q_2\)ですから、熱効率は(3-22)式より、\(\frac{Q_1-Q_2}{Q_1}\)となります。

 

　これで答は得られましたが、
\(B\to C\)では体積が増加しますから、外部に仕事をしています。
\(D\to A\)では減少していますから、外部から仕事をされています。
これらの仕事を考えなくて良いことも確認しておきましょう。

 

　そこで、表を使って考えてみます。
　この表で、\(B\to C\)で外部にした仕事を\(W_1\)、\(D\to A\)で気体が外部からされた仕事を\(W_2\)としています。

過程		内部エネルギー変化 \(\Delta U=\frac{3}{2}\Delta (pV)\)	外部にした仕事 \(W_{out}\)	気体が吸収した熱量 \(Q=\Delta U+W_{out}\)
\(A\to B\)	等温	\(0\)	\(Q_1\)	\(Q_1\)
\(B\to C\)	断熱	\(-W_1\)	\(W_1\)	\(0\)
\(C\to D\)	等温	\(0\)	\(-Q_2\)	\(-Q_2\)
\(D\to A\)	断熱	\(W_2\)	\(-W_2\)	\(0\)
1サイクル	合計	\(W_2-W_1\)	\(Q_1-Q_2+W_1-W_2\)	\(Q_1-Q_2\)

 

　さて、1サイクルの内部エネルギーの合計は\(0\)であるはずです。
つまり、\(W_1=W_2\)ですから、ふたつの断熱過程での仕事の和は\(0\)です。

 

　したがって、外部にした仕事の1サイクルの合計は、
\begin{equation} Q_1-Q_2+W_1-W_2=Q_1-Q_2 \end{equation}
となります。
　ですから、断熱変化での仕事を、熱効率の式の中に含める必要はなかったわけです。

 

　さて、図3-11のサイクルは、カルノーサイクルと呼ばれ、最も効率の良い熱機関です。
現実的にカルノーサイクルを持つエンジンを作ることはできないのですが、比較する基準として用いられます。

 

　高校物理の範囲を超えますが、カルノーサイクルの効率\(e'\)は、状態\(A、B\)の絶対温度を\(T_1\)（高温側）、状態\(C、D\)の絶対温度を\(T_2\)（低温側）として、
\begin{eqnarray} e'&=&\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1} \\
&=&1-\frac{T_2}{T_1} \tag{3-23}
\end{eqnarray}
であることが知られています。　

 

 

 

　【例題1＆例題1’】

 

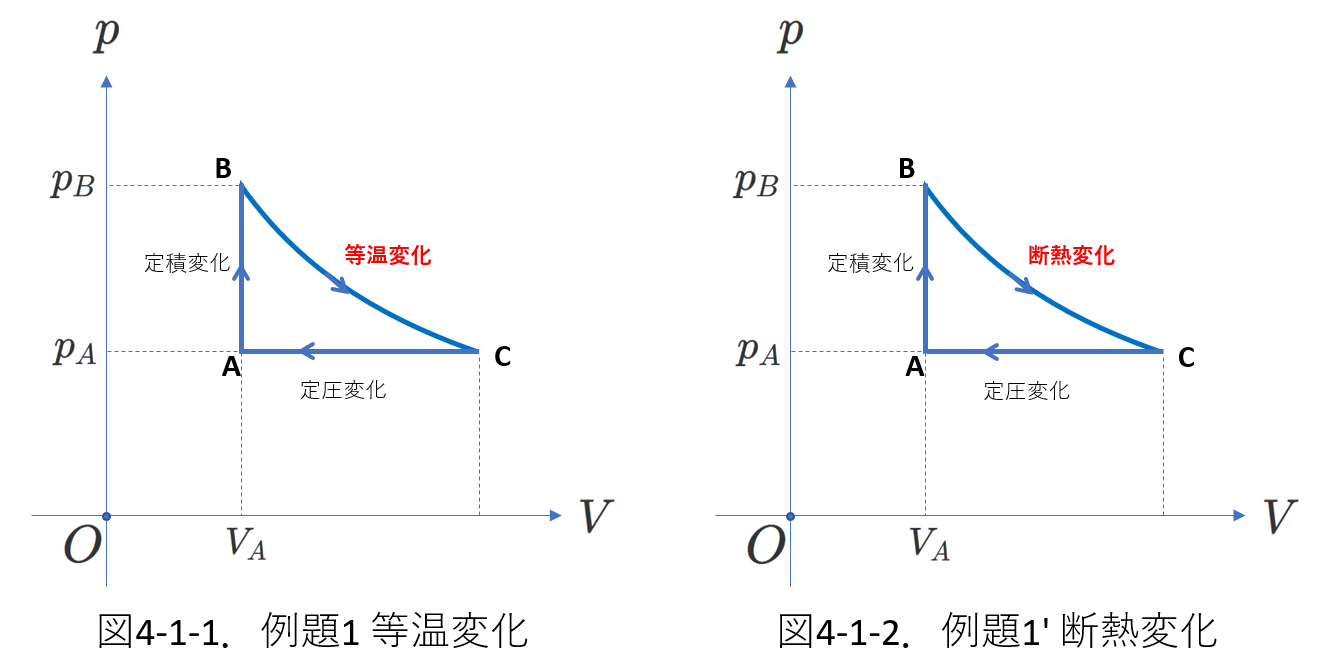
　最初の例題を図4-1-1と図4-1-2に示します。

 

　このサイクルの熱効率を求める問題です。
図で\(B\to C\)の過程は、図4-1-1は等温変化、図4-1-2は断熱変化です。
ここでは、ふたつの過程を比べて考えます。
　なお、気体は単原子分子理想気体を考えます。

 

　熱機関の効率を求めるには、気体に入った熱量と正味の仕事（または、気体に入った熱量と出た熱量）を求めます。

 

　ここで、もう一度、熱効率の公式をあげておきましょう。
\begin{eqnarray}
e&=&\frac{W}{Q_{in}} \tag{4-1} \\
e&=&\frac{Q_{in}-Q_{out}}{Q_{in}} \tag{4-2} \\
ただし、e&:&熱効率 \\
W&:&熱機関がした仕事（された仕事を差し引いた正味の仕事） \\
Q_{in}&:&（高温の物体から）吸収した熱量 \\
Q_{out}&:&（低温の物体に）放出した熱量、捨てた熱量
\end{eqnarray} 　

 

　熱機関がした仕事は、\(A\to B\to C\to A\)の図形の面積を求めることになります。
等温変化でも断熱変化でも、\(B\to C\)は外部に仕事をしています。
また、\(C\to A\)は外部から仕事をされています。

 

温度の変化についていえば、\(A\to B\)は、温度は上昇（内部エネルギーが増加）し、仕事は\(0\)、なので、気体は熱を吸収します。
\(C\to A\)では、温度は下降（内部エネルギーは減少）し、気体は外部から仕事をされているので、気体は熱を放出しています。

 

 

　図4-1-1と図4-1-2では、状態\(A\)、状態\(B\)の状態は同じです。
つまり、\(p_A、p_B、V_A\)が与えられていて、図4-1-1と図4-1-2で同じ値です。
また、どちらの場合も、[状態\(C\)の圧力]\(=p_A\)です。
つまり、どちらの場合でも、\(A\to B\)は定積変化、\(C\to A\)は定圧変化です。

 

　これだけの条件で、熱機関の効率（熱効率）を求めることを考えます。

 

　ふたつの過程（変化）を比較した場合、等温変化では、[状態\(B\)の温度]=[状態\(C\)の温度]であるのに対して、断熱変化では熱の出入りがないので気体が外部に仕事をした分、内部エネルギーが減少します。
つまり、温度が下がります。
　以上のことを考えると、[等温変化の状態\(C\)の絶対温度]\(\gt\)[断熱変化の状態\(C\)の絶対温度]であり、
[等温変化の状態\(C\)の体積]\(\gt \)[断熱変化の状態\(C\)の体積]です。
　ということは、\(A\to B\to C\to A\)の面積は、断熱変化の方が小さいです。
ただし、これだけでは、熱効率の大小は判断できません。

 

　さて、\(A\to B\)は定積変化で、外部へは仕事をしません。それでも、圧力が高まるのは、温度が上がったためですから、気体は熱を吸収したはずです。
この気体が吸収した熱量\(Q_{AB}\)は簡単に求めることができます。
\begin{eqnarray} Q_{AB}&=&[内部エネルギーの変化量] \tag{4-3} \\
&=&\frac{3}{2}\left(p_B-p_A\right)V_A 　　\tag{4-4} \\
&(&(4-4)式は、単原子分子理想気体の場合)　　 \end{eqnarray}

 

 

　\(C\to A\)は定圧変化で、外部から仕事され、かつ、内部エネルギーは減少します。
ゆえに、気体は熱を放出します。

 

状態\(C\)の体積を\(V_C\)として、
\begin{eqnarray} 気体が外部にする仕事W_{CA}は&、&p_A(V_A-V_C) \tag{4-5} \\
+)　　内部エネルギーの変化量\Delta U_{CA}は&、&\frac{3}{2}(p_AV_A-p_AV_C) \\
-----------------------&-&------- \\
吸収した熱量Q_{CA} は&、&\frac{5}{2}p_A(V_A-V_C)　　\tag{4-6}
\end{eqnarray}
ここで、\(Q_{CA}\lt 0\)であることに注意、気体は熱を放出しています。

 

 

　では、個々に考察していきます。
　最初に等温変化の場合を考えます。

 

　【例題1】等温変化の場合

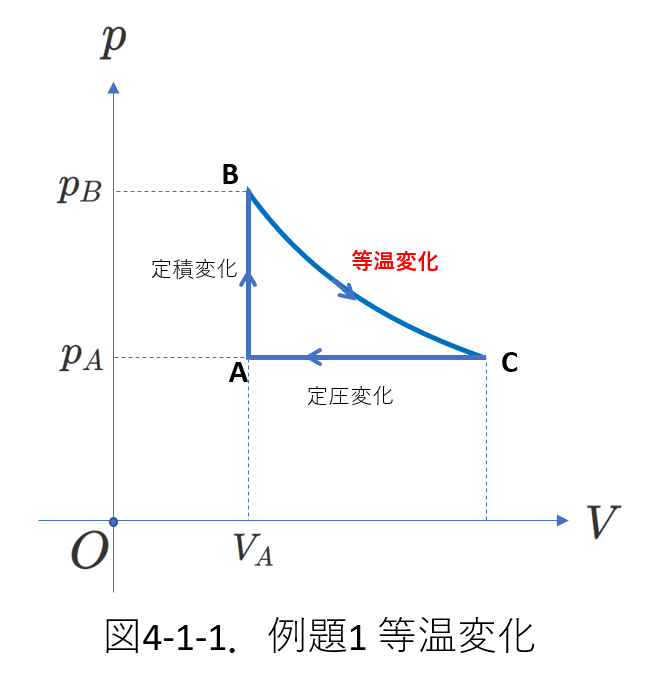
　さて、熱効率を求めるには何が分かればよいでしょうか。

 

　ひとつは状態\(C\)の体積\(V_C\)です。

 

　等温変化ですから、[状態\(B\)の絶対温度：\(T_B\)]=[状態\(C\)の絶対温度：\(T_C\)]です。
\(T_B\)は、状態\(B\)の圧力\(p_B\)と体積\(V_A\)から求まります。
そして、状態\(C\)の圧力\(p_A\)と\(T_C\)から、\(V_C\)が求まります。

 

①　\(V_C\)がわかれば、（4-5）式から\(C\to A\)で気体が外部にする仕事\(W_{CA}\)がわかります。このとき、(4-1)式から熱効率\(e\)を求めることを考えます。
②　また、(4-6)式から\(C\to A\)で気体が放出する熱量\(-Q_{CA}\)がわかります。このとき、(4-2)式から\(e\)を求めることを考えています。

 

　①の場合、さらに、\(B\to C\)での気体が外部にする仕事\(W_{BC}\)を知る必要があります。
また、②の場合、\(B\to C\)で吸収する熱量\(Q_{BC}\)を知る必要があります。
等温変化では、気体が外部にした仕事に相当する熱量を吸収することで温度が一定に保たれます。
つまり、熱力学第一法則を考えると、内部エネルギーの変化量は\(0\)ですから、\(Q_{BC}=W_{BC}\)です。
したがって、①の場合でも②の場合でも、\(W_{BC}\)を知る必要があります。

 

　等温変化は\(p-V\)グラフ上で直線ではないので、単純に面積を計算することはできません。　
しかし、積分を使えば、\(W_{BC}\)を計算することができます。

 

　状態\(B\)から状態\(C\)への\(p-V\)グラフの式は、状態方程式から、
\begin{equation} p=\frac{nRT}{V} \tag{4-7} \end{equation}
です。
　等温変化ですから、\(T=一定=T_B\)で、状態\(B\)での状態方程式から\(nRT=p_BV_A\)です。
　これより、
\begin{eqnarray} p&=&\frac{p_BV_A}{V} \tag{4-8} \\
したがって、W_{BC}&=&\int_{V_B}^{V_C} pdV=\int_{V_B}^{V_C} \frac{p_BV_A}{V}dV \tag{4-9}
\end{eqnarray}

 

　数学では、この積分は高校レベルで計算できますが、物理では積分をすることはないようです。（もちろん、微分積分の知識を活用することで、考察が楽になることが多いので、物理においても微分積分を意識していたほうが良いです。）
　さて、具体的な問題では、積分を避けて\(W_{BC}\)が分かっているものとして、熱効率を求める問題があります。

 

　そこで、(4-9)]式の積分は置いておいて、ここでは、\(W_{BC}\)が分かっているものとして、（4-1）式をもとに、熱効率\(e\)を求めます。
　気体が外部から熱を吸収するのは、\(A\to B\)と\(B\to C\)の過程です。
\begin{eqnarray}
A\to B&：&[内部エネルギーの変化]\ \Delta U_{AB}=\frac{3}{2}(p_B-p_A)V_A \tag{4-10} \\
&&[外部にした仕事]=0 \\
　　　　　 &&[吸収した熱量]\ Q_{AB}=[内部エネルギーの変化]=\frac{3}{2}(p_B-p_A)V_A \tag{4-4} \\
\\
B\to C&：&[内部エネルギーの変化量]=0 \\
　　　　&&[外部にした仕事]=W_{BC} \tag{4-11} \\
&&[吸収した熱量]\ Q_{BC}=[内部エネルギーの変化量]+[外部にした仕事]=W_{BC} \tag{4-12}　　　
\end{eqnarray}

 

　これで、（4-1）式を使って熱効率計算するに必要な項目がすべて得られました。
（4-4）、（4-5）、（4-11）、(4-12)式を使って、
\begin{eqnarray} e&=&\frac{W}{Q_{in}} \\
&=&\frac{W_{BC}+W_{CA}}{Q_{AB}+Q_{BC}} \\
&=&\frac{W_{BC}+(V_A-V_C)p_A}{\frac{3}{2}(p_B-pA)V_A+W_{BC}} \tag{4-13}
\end{eqnarray}

 

 

 

【例題1’】　次に、断熱変化の場合です。
　\(B\to C\)が断熱変化の場合、この過程で気体への熱の出入りはありません。
したがって、熱効率を（4-2）式で求める場合、\(B\to C\)での仕事を考える必要がありません。
つまり、\(Q_{AB}\)と\(Q_{CA}\)が与えられていれば\(B\to C\)の過程を考えることなく、直ちに熱効率が計算できます。
ここは意識しておきましょう。

 

　しかしながら、熱効率を求めるには、\(V_C\)を知る必要があります。

 

　断熱過程では、圧力\(p\)と体積\(V\)の間にポアソンの法則の関係があります。
ポアソンの法則は、
\begin{eqnarray} pV^{\gamma}=一定　\tag{4-14} \\
ここで、\gamma=\frac{C_p}{C_V} \tag{4-15} \\
C_p：定圧モル比熱 \\
C_V：定積モル比熱
\end{eqnarray}
ところで、メイヤーの関係式（\(C_p=C_V+R\)）を考えると、\(\frac{C_p}{C_V}=\gamma\gt 1\)です。
単原子分子理想気体の場合、\(\frac{5}{3}\)です。

 

 

 

　例題に戻って、ポアソンの法則から、
\begin{eqnarray} p_BV_A^{\gamma}&=&p_AV_C^{\gamma} \tag{4-17} \\
V_C&=&\sqrt[\gamma]{\frac{p_B}{p_A}}V_A \tag{4-18}
\end{eqnarray}

 

　したがって熱効率は、（4-2）式を元に、（4-4）、(4-6)、(4-18)使うと、
\begin{eqnarray} e&=&\frac{Q_{in}-Q_{out}}{Q_{in}} \tag{4-1} \\
&=&\frac{\frac{3}{2}(p_B-p_A)V_A-(-Q_{CA})}{\frac{3}{2}(p_B-p_A)V_A} \\
&=&\frac{\frac{3}{2}(p_B-p_A)V_A-\frac{5}{2}(V_C-V_A)p_A}{\frac{3}{2}(p_B-p_A)V_A} \\
&=&\frac{\frac{3}{2}(p_B-p_A)V_A-\frac{5}{2}(\sqrt[\gamma]{\frac{p_B}{p_A}}V_A-V_A)p_A}{\frac{3}{2}(p_B-p_A)V_A} \\
&=&\frac{\frac{3}{2}(p_B-p_A)V_A-\frac{5}{2}(\sqrt[\gamma]{\frac{p_B}{p_A}}-1)p_AV_A}{\frac{3}{2}(p_B-p_A)V_A} \tag{4-19} \\
&=&\frac{3p_B+\left(2-5\sqrt[\gamma]{\frac{p_B}{p_A}}\right)p_A}{3(p_B-p_A)}
\end{eqnarray}
　となります。

 

 

 

 

 

 

 

例題2

 

　立命館大学の入試問題に面白いものがありましたので、取り上げます。
　下図を参照してください。
　この熱機関の効率を求める問題です。

 

 

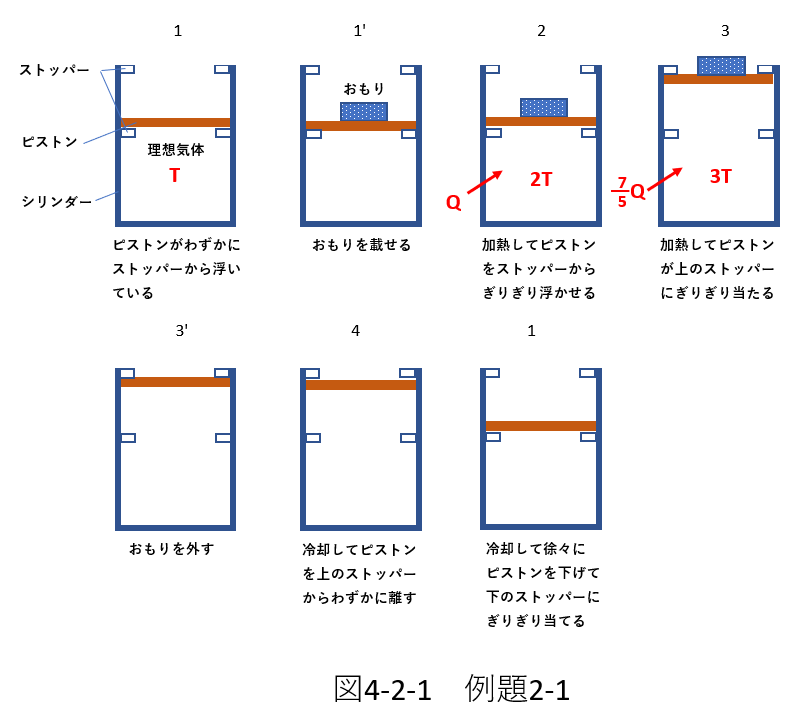
　各過程を説明します。
１．ふたつのストッパーを持つシリンダーに、ストッパーの間に滑らかに動くピストンが嵌められています。　今、ピストンが下のストッパーからわずかに浮いた状態で静止しています。シリンダー内に理想気体が封じられていて、その気体の絶対温度は\(T\)です。
１’．ピストンの上に重りを載せます。
２．シリンダー内の気体に熱量を加えて、下のストッパーからわずかに浮いた状態にします。気体が吸収した熱量は\(Q\)で、絶対温度は\(2T\)となりました。
３．さらに、熱量を加えて、ピストンをゆっくり上昇させ、上のストッパーにぎりぎり触れたところでピストンは静止しました。気体が吸収した熱量は\(\frac{7}{5}Q\)で、この結果気体の絶対温度は\(3T\)となりました。
３’．おもりをピストンから降ろしました。
４．気体を冷却してピストンを上のストッパーからわずかに下がるようにしました。
１．徐々に冷却して、ピストンをゆっくりと下降させて、１の状態に戻します。

 

　この問題の面白い点は、
・情報が非常に少ない。
　気体の圧力や体積については何も情報がありません。
　絶対温度と一部の過程の熱量だけです。
　しかも後半になると、それらの情報もなくなります。
・単原子分子理想気体ではなく、理想気体です。
　単原子分子理想気体でないので、[内部エネルギーの変化量]=\(\frac{3}{2}nR\Delta T\)　が使えません。
もちろん、[内部エネルギーの変化量]=\(\frac{3}{2}\Delta (pV)=\frac{3}{2}(p_2V_2-P_1V_1)\)も使えません。
理想気体では、内部エネルギーの変化量\(\Delta U\)は、
\begin{equation} \Delta U=nC_V\Delta T \end{equation}
と表します。
ここで、\(C_V\)は定圧モル比熱です。

 

 

　これだけの情報から、気体がする仕事、あるいは、気体が放出する熱量を評価しなければなりません。
　とはいえ、条件をもう少し丁寧に見ていくことにします。
便宜上、１での気体の圧力を\(p_1\)、体積を\(V_1\)と仮定します。
これらの文字は、答に使うことはできないので、熱効率を計算する途中で消去されるものと考えておきます。

 

　１の状態ではピストンは静止していますから、外部の圧力と気体の圧力がつり合っています。

 

　１’でおもりを載せると、重りに働く重力により、１のつり合いがなくなるので、ピストンは下のストッパーに押し付けられます。
この状態では、ストッパーからの抗力が生じて再びピストンに働く力がつりあいます。
さて、１と１’では、気体の圧力も体積も変化していません。
さらに言えば、絶対温度も同じです。
つまり、\(p-V\)グラフ上では同じ点で表されます。

 

　２で\(Q\)の熱量を与えて、ふたたびピストンをわずかに浮かせました。
　ピストンの位置は１や１’と同じですが、２では、ピストンには外部の圧力と内部の気体の圧力に加えて、おもりの重力が加わってきますから、気体の圧力は\(p_1\)よりも大きくなっているはずです。
気体の体積は変わらずに、絶対温度が2倍になっているので、圧力も2倍になっているとわかります。
すなわち、\(2p_1\)です。そして、体積一定のまま圧力が変化（増加）しているので、\(1'\to 2\)は定積変化です。

 

　３では、徐々に熱量を加え、おもりをゆっくり持ち上げました。
しかし、ピストンにはたらく力のつりあいの条件は、２と同じですから、圧力は\(2p_1\)です。
体積は後ほど検討します。
\(2\to 3\)の過程では、おもりには「重力」と「外部の気体の圧力による力」と「気体の圧力による力」がつりあった状態で、体積が変化しますから、これは、定圧変化です。

 

　３’では、ピストンに働く重りの重力がなくなるので、気体の圧力が外部気体の圧力に勝り、ピストンは上のストッパーに押し付けられます。そして、3と3’は、体積と圧力が同じ（したがって絶対温度も同じ）ですから、\(pV\)グラフ上では同じ点で表されます。

 

　４の状態は、外部気体の圧力と気体の圧力がつり合った状態ですから、気体の圧力は、１の状態と同じで、\(p_1\)です。\(3'\to 4\)は定積変化です。

 

　\(4\to 1\)は定圧変化です。

 

　以上の考察で、各状態での圧力が確認できました。（各状態での圧力を\(p_1\)を用いて表すことができました。）
それをまとめたものが、次の図4-2-2です。

 

 

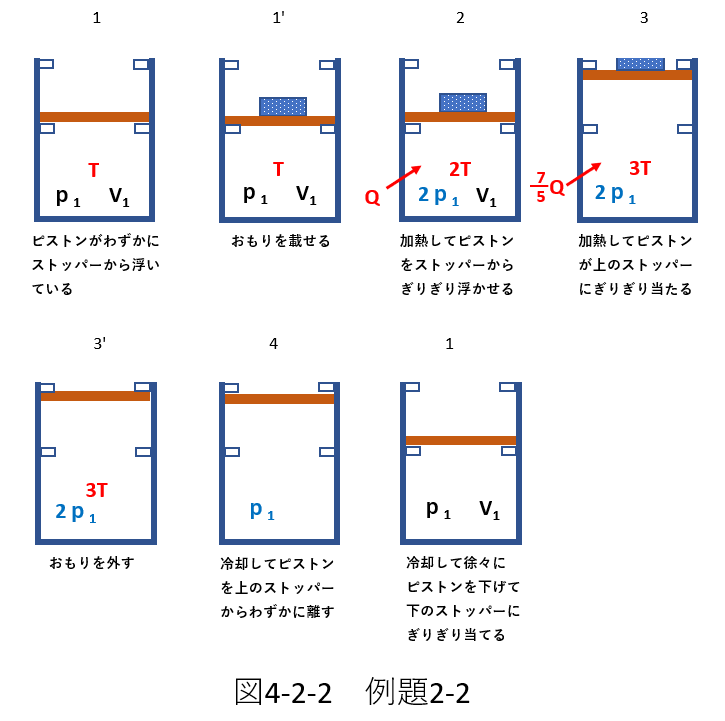
　各状態のまだ不明なところについては、状態方程式を使って考えます。
１，２，３，４の状態方程式は次のようになります。
ここで、状態２での気体の圧力を\(p_2\)、状態３での気体の体積を\(V_3\)、状態４での気体の絶対温度を\(T_4\)としています。
\begin{eqnarray} 状態１&：&p_1V_1=nRT \tag{4-20} \\
状態２&：&p_2V_1=nR\cdot 2T \tag{4-21} \\
状態３&：&p_2V_3=nR\cdot 3T \tag{4-22} \\
状態４&：&p_1V_3=nRT_4 \tag{4-23}
\end{eqnarray}

 

状態１と状態２の状態方程式より、\(p_2=2p_1\)です。
状態２と状態３の状態方程式から、\(V_3=\frac{3}{2}V_1\)です。
状態３と状態４の状態方程式と\(p_2=2p_1\)から、\(T_4=\frac{3}{2}T\)です。

 

　ここは、たとえば、状態1と状態2に、ボイルシャルルの法則を適用して、\(\frac{p_1V_1}{T}=\frac{p_2V_1}{2T}\)　より、\(p_2=2p_1\) と、計算することもできます。

 

これらの結果を書き入れたものが次の図4-2-3です。

 

 

 

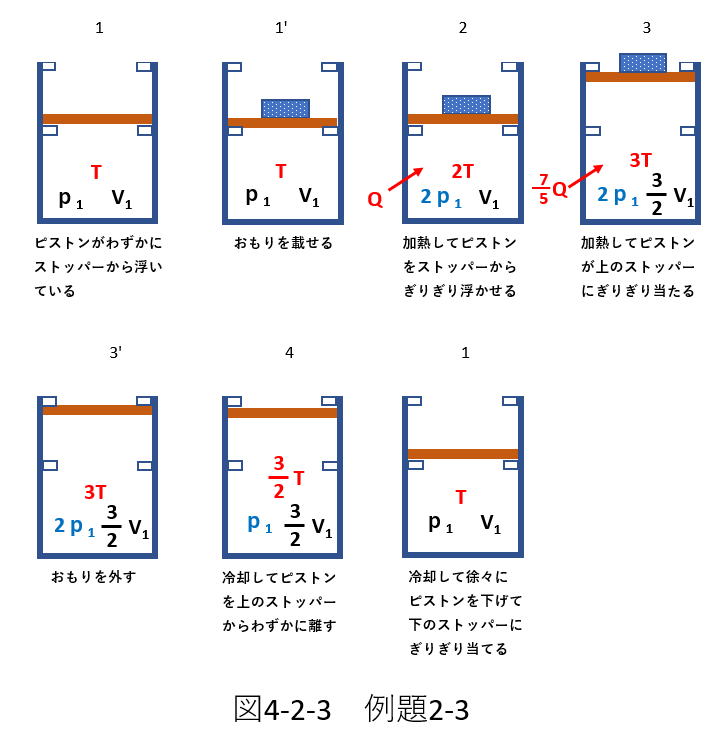
　今までの考察をもとに\(p-V\)グラフを描けば右下の図4-3のようになります。

 

 

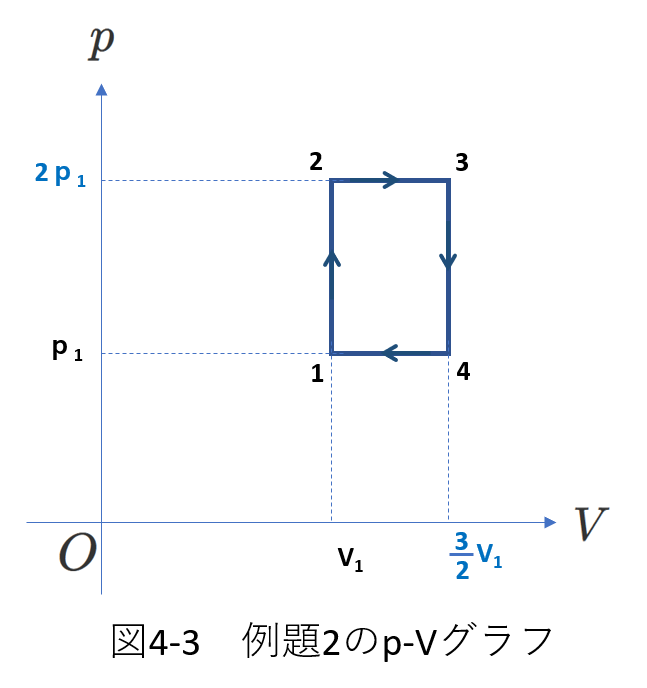
　状態１と状態１’は気体の状態は同じですから、\(p-V\)グラフ上で１として示してあります。
同様に、３と３’は３で表されています。

 

　\(1\to 2\)では気体は仕事せずに内部エネルギーが増加するので、気体は熱を吸収します。（題意通りで、吸収する熱量は\(Q\)です。）

 

　\(2\to 3\)は気体は外部に仕事をしたうえに内部エネルギーも増加するので、気体は熱を吸収しています。（これも題意どおりで、吸収する熱量は\(\frac{7}{5}Q\)です。）

 

　\(3\to 4\)は、気体は外部に仕事をせずに内部エネルギーが減少していますから、気体は熱を放出しています。

 

　\(4\to 1\)は、気体は外部から仕事をされたうえに内部エネルギーを減少させていますから、気体は熱を放出します。

 

　これらのことから、熱効率の式の分母は、\(Q+\frac{7}{5}Q\)であることがわかります。
　分子は、正味の仕事で、図4-3の四角の面積を求めるか、\(3\to 4\to 1\)で気体が放出する熱量を求めるかです。

 

　楽そうなので、四角形の面積を求めるほうで計算します。
四角形の面積（\(=W\)）は、
\begin{eqnarray} W&=&(2p_1-p_1)(\frac{3}{2}V_1-V_1) \\
&=&\frac{1}{2}p_1V_1 \tag{4-24} \\
したがって、熱効率は、e&=&\frac{\frac{1}{2}p_1V_1}{\frac{12}{5}Q} \tag{4-25}
\end{eqnarray}
となります。
　しかし、これでは仮定したままの\(p_1\)と\(V_1\)が消去されません。
\(p_1\)と\(V_1\)を消去するには、これらと\(Q\)の関係が求まればよいだろうと、そしてそれには熱力学の第一法則を使えばよいと想像できます。
\(1'\to 2\)に熱力学の第一法則を用いると、
\begin{eqnarray} Q&=&nC_V(2T-T)=nC_VT \tag{4-26} \end{eqnarray}
　これでは、まだ、\(Q\)と\(p_1V_1\)の関係になっていません。

 

　そこで、\(2\to 3\)についても熱力学の第一法則を適用してみます。
\begin{eqnarray} 　\frac{7}{5}Q&=&nC_V(3T-2T)+2p_1(\frac{3}{2}V_1-V_1) \\
&=&nC_VT+p_1V_1 \\
この式と（4-26）式を用いれば、\\
p_1V_1&=&\frac{7}{5}Q-nC_VT \\
&=&\frac{7}{5}Q-Q=\frac{2}{5}Q　　\tag{4-27}
\end{eqnarray}
　これを、（4-25）式に代入します。

 

\begin{eqnarray}
e&=&\frac{\frac{1}{2}p_1V_1}{\frac{12}{5}Q} \tag{4-25} \\
&=&\frac{\frac{1}{2\cdot }\frac{2}{5}Q}{\frac{12}{5}Q} \tag{4-28} \\
&=&\frac{1}{12}
\end{eqnarray}

 

 

 

 

 

 

 

例題3

 

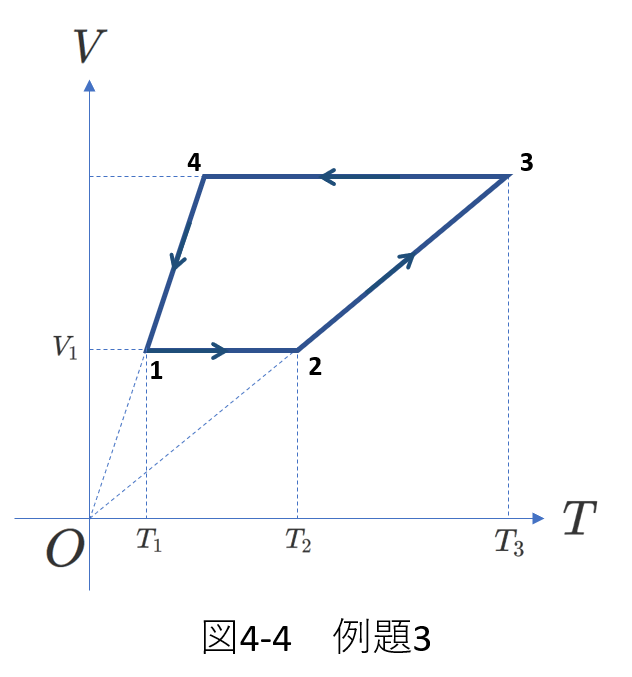
　例題3も熱効率を求める問題です。
　そして、熱サイクルは、右図のように、\(V-T\)グラフで与えられています。気体は単原子分子理想気体です。

 

　グラフで注意するのは、状態2と3を結ぶ直線、および、状態4と1を結ぶ直線が原点を通るということです。

 

　解法を考える前に、各状態の確認をします。
　\(1\to 2\)：定積仮定ですから外部にする仕事は\(0\)、、絶対温度は上昇していますから内部エネルギーは増加、気体は熱を吸収しています。

 

 

　\(2\to 3\)：絶対温度は増加（内部エネルギーは増加）、体積は絶対温度に比例して増加していますから、気体は外部に仕事をしています。これらのことから気体は熱を吸収しています。

 

　\(3\to 4\)：定積変化で絶対温度は減少。気体は仕事をせず、内部エネルギーは減少していますから、気体は熱を放出しています。

 

　\(4\to 1\)：絶対温度は減少（内部エネルギーは減少）、体積は絶対温度に比例して減少していますから、気体は外部から仕事をされていて、熱を放出しています。

 

　\(2\to 3\) 、および、\(4\to 1\)で[体積]と[絶対温度]が比例する変化がどのような変化であるかを考えます。
　状態方程式を変形して、
\begin{equation} V=\frac{nR}{p}T \tag{4-33} \end{equation}
　これより、\(V\)と\(T\)が比例することは、\(\frac{nR}{p}\)が一定、すなわち、\(p=[一定]\)であることから、この変化は定圧変化であることがわかります。

 

　状態間の変化がどんなものかがわかったので、各状態について何が分かるかを考えます。使うのは状態方程式と各変化の内容です。

 

　状態1と状態2は、[体積]と[絶対温度]がわかっているので、[圧力]もわかります。

 

　\(2\to 3\)が定圧変化であることから、状態3の[圧力]がわかります。[絶対温度]もわかっているので[体積が]が計算できます。

 

　\(3\to 4\)が定積変化であることから状態4の[体積]が、\(4\to 1\)が定圧変化であることから状態4の[圧力]が、そして、それらから、[絶対温度]がわかります。
　以上で、全ての状態の[体積][絶対温度:][圧力]がわかりました。

 

　全ての変化が定積変化か定圧変化である（等温変化や断熱変化がない）ので、熱効率は容易に計算できます。

 

　\(p-V\)グラフの方が分かりやすいので、図4-4を\(p-V\)グラフに変換して、図4-5が得られます。

 

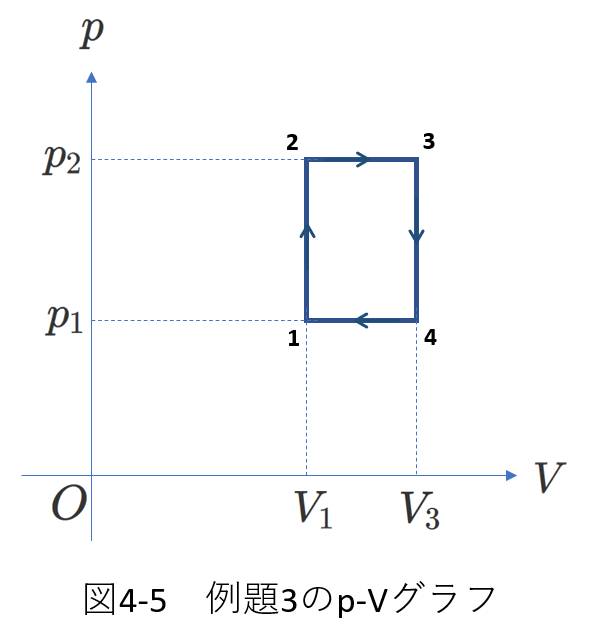
　\(p-V\)グラフを描くと、見通しが良くなりますね。

 

　熱効率の（4-1）式　\(e=\frac{W}{Q_{in}}\)において、分子\(W\)は、
\begin{equation} W=(p_2-p_1)(V_3-V1) \tag{4-34} \end{equation}

 

　気体が熱を吸収する過程は、\(1\to 2\)と\(2\to 3\)です。
それぞれの変化で気体が吸収する熱量を\(Q_{12}、Q_{23}\)とすれば、熱力学の第一法則より、
\begin{eqnarray} Q_{12}&=&\frac{3}{2}(p_2-p_1)V_1 \tag{4-35} \\　
Q_{23}&=&\frac{3}{2}p_2(V_3-V_1)+p_2(V_3-V_1) \\
&=&\frac{5}{2}p_2(V_3-V_1) \tag{4-36}
\end{eqnarray}　

 

　以上より、熱効率\(e\)は、
\begin{eqnarray} e&=&\frac{W}{Q_{in}} \\
&=&\frac{(p_2-p_1)(V_3-V1) }{Q_{12}+Q_{23}} \\
&=&\frac{(p_2-p_1)(V_3-V1) }{\frac{3}{2}(p_2-p_1)V_1+\frac{5}{2}p_2(V_3-V_1)} \tag{4-37}
\end{eqnarray}

 

　では、（4-37）式の\(p_1、p_2、V_3\)を求めておきます。
\begin{eqnarray}
状態1：p_1V_1&=&nRT_1 \tag{4-38} \\
状態2：p_2V_1&=&nRT_2 \tag{4-39} \\
状態3：p_2V_3&=&nRT_3 \tag{4-40} \\
以上より、p_1&=&\frac{nRT_1}{V_1}、p_2=\frac{nRT_2}{V_1}、 V_3=\frac{nRT_3}{p_2}=\frac{V_1T_3}{T_2} \tag{4-41}
\end{eqnarray}
　これらを（4-37）式に代入して整理すると、\(nR\)は消去されて、
\begin{equation} e=\frac{2(T_2-T_1)(T_3-T_2)}{T_2(5T_3-2T_2-3T_1)} \tag{4-42} \end{equation}

 

　なお、(4-37)式に代入する際には、(4-37)式の形から判断して、\((p_2-p_1)\)と\((V_3-V_1)\)を最初に計算し、その結果を（4-37）式に代入すると、多少計算が楽になります。
　また、もう気が付いていると思いますが、この例題は、「Ⅲ　ｐ-Vグラフの基本　熱力学第一法則　Ⅱ」の「４．熱機関の効率」の例題１と同じ内容です。
ここでは、\(V-T\)グラフが使われましたが、例題１では\(p-V\)グラフが使われていました。

 

 

関連ページ

p-Vグラフ　Ⅰ

P-Vグラフについて、状態と状態変化に注目し、熱力学第一法則や状態方程式との関連を説明しています。