Ⅰ.単振動の運動の様子・・・加速度・速さ・位置の関係
1.単振動の式とグラフ
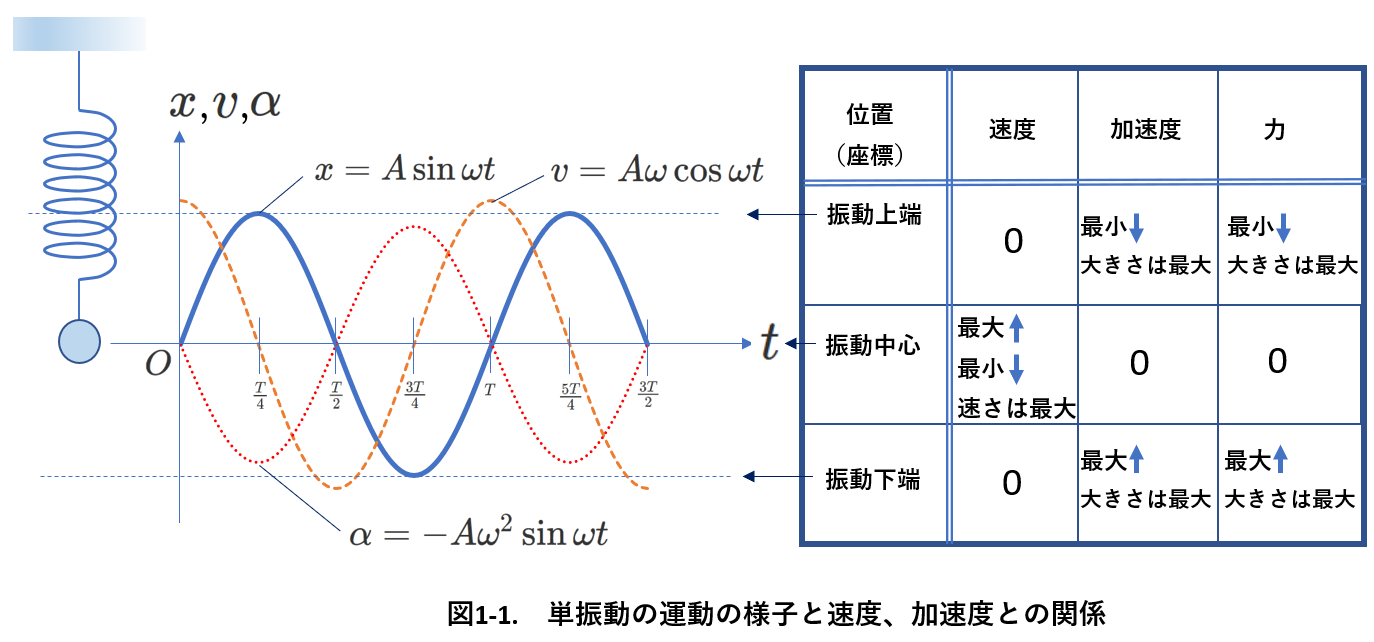
図1-1に、単振動のグラフを示します。
天井に吊るされたばねにおもりが接続されて単振動をしているときの、
時間\(t\)が、\(0\)から\(\frac{3}{2}T\)(\(T\)は単振動の周期)の間について、
おもりの位置(座標)\(x\)、速度\(v\)、加速度\(\alpha\)をひとつのグラフに表しています。
ここで、振動の中心は\(x=0\)にあり、振幅は\(A\)であり、
おもりの位置(座標)\(x\)は、\(x=A\sin\omega t\)と表されるとします。
つまり、\(t=0\)で、\(x=0\)(振動中心)、\(+x\)向き(\(v\gt 0\))に最大速度を持つと考えています。
そして、\(\omega\)は、単振動の角振動数です。
このとき、速度\(v\)と加速度\(\alpha\)は次にように表されます。
\begin{eqnarray}
x&=&A\sin\omega t \tag{1-1} \\
v&=&\frac{dx}{dt}=A\omega \cos \omega t \tag{1-2} \\
\alpha&=&\frac{dv}{dt}=-A\omega^2\sin\omega t \tag{1-3}
\end{eqnarray}
仮に、振動の中心が\(x=x_0\)にあるとすれば、(1-1)~(1-3)式は次のようになります。
\begin{eqnarray}
x&=&A\sin\omega t+x_0 \tag{1-4} \\
v&=&\frac{dx}{dt}=A\omega \cos \omega t \tag{1-2} \\
\alpha&=&\frac{dv}{dt}=-A\omega^2\sin\omega t \tag{1-3}
\end{eqnarray}
\(v\)、\(\alpha\)については、振動中心が変わっても、式は同じです。
さて、おもりが振動の端(上端、下端)、あるいは、振動中心にあるときの、速度や加速度が
どのようにあらわされるかを、知っておくことが大事です。
図1-1の右の表を見てください。
おもりが振動中心にあるとき、速さは最大で、加速度は\(0\)です。
この時の速さ\(v_{max}\)は、\(A\omega\)と表されます。
速さが最大なのに加速度が\(0\)ということを、奇妙に感じるかもしれません。
「速さと加速度は比例する」という錯覚を起こさないようにしましょう。
おもりが振動の端にあるとき、速度は\(0\)、加速度の大きさは最大になります。
このときの加速度の大きさ\(\alpha_{max}\)は、\(A\omega^2\)と表されます。
図1-1の\(x\)のグラフは、振動の端(上端、下端)で極値を取ります。
つまり、振動の端では、\(\frac{dx}{dt}=0\)ですから、\(v=0\)です。
※一般的な運動を考えたとき、運動の端(つまり、座標の最大値・最小値、あるいは、最高点・最低点)では、
座標\(x\)が極値を持つわけですから、そこでは、速度\(v=0\)となります。
言い変えると、速度\(v=0\)という条件から、運動の端(到達点)を求めることができます。
この考えは、放物運動(物を投げ上げたときの運動)、単振動、宇宙での到達点などに使うことができます。
図1-1の右の表には、力の欄があります。
図では、ばねが鉛直に吊るされているので、力とは、ばねの弾性力と重力の合力になります。
そして、運動方程式\(m\alpha=F\)からわかるように、
力\(F\)と加速度\(\alpha\)は、向きが同じで、比例関係があります。
したがって、表の加速度と力の欄の内容は同じものになります。
このことを、「加速度と力は同じ位相である」と言うこともできます。
位相が同じとは、加速度が最大ならば力も最大、加速度が\(0\)ならば力も\(0\)ということです。
図1-1から、加速度と速度は同じ位相ではないことがわかります。
加速度と位置(座標)も同じ位相ではありません。
おもりが、振動の端にあるとき、
おもりが受ける力は最大で、したがって、加速度も最大になります。
おもりが、振動の中心にあるとき、
おもりが受ける力は\(0\)(この瞬間、力はつりあっていることになります)、したがって、加速度も\(0\)になります。
式を整理しておきます。
\(\omega=\frac{2\pi}{T}\)、\(\omega=2\pi f\) (\(f\) は、振動数)、\(f=\frac{1}{T}\)
\(v_{max}=A\omega\)
\(\alpha_{max}=A\omega^2\)
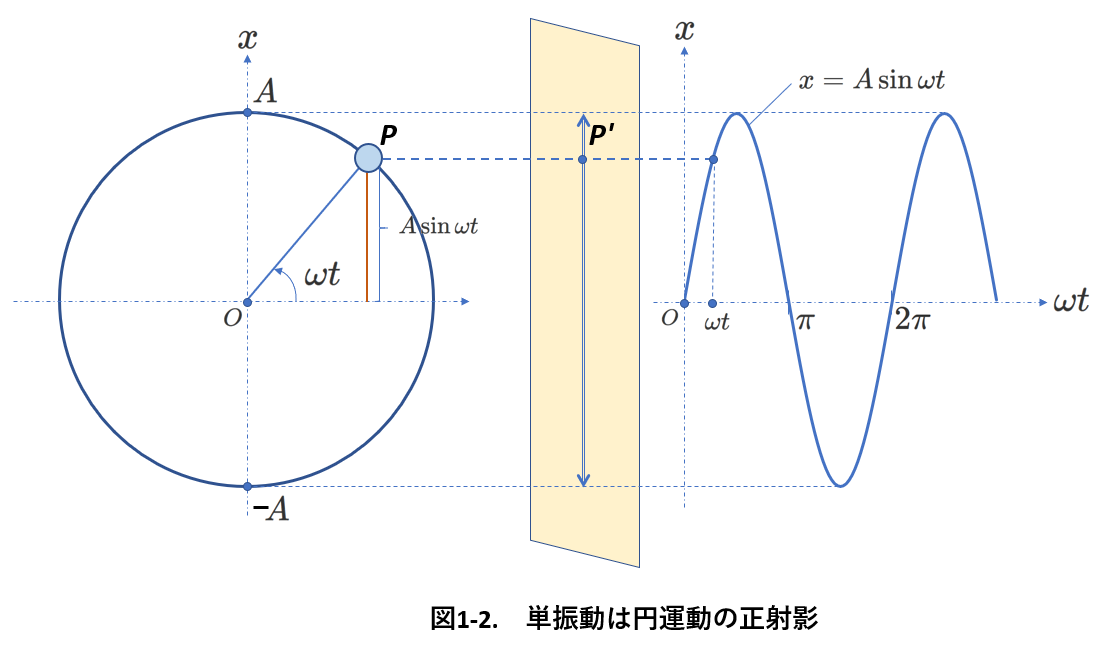
2.単振動は円運動の正射影
単振動は、形式的に、等速円運動の正射影と考えることができます。
図1-2にその様子を示しました。
物体\(P\)が点\(O\)を中心に半径\(A\)で等速円運動をしているものとします。
角速度を\(\omega\)とすると、\(P\)の速さは\(A\omega\)と表されます。
図1-2の左側の円運動の図では、紙面に平行な平面内で\(P\)が等速円運動をしています。
中央黄色のスクリーンは紙面に垂直で\(x\)軸に平行な平面で、
\(P\)の中央黄色のスクリーンへの正射影が\(P'\)です。
\(P'\)はスクリーン上で振動をします。
図1-2の右側には、\(P'\)の運動をグラフに表しています。
図1-1の横軸は時間\(t\)を表し、1回振動すると、時間は1周期(\(T\))だけ経過します。
一方、図1-2の横軸は、\(\omega t\)を表し、1回振動すると、\(\omega t\)(位相)は\(2\pi\)だけ変化します。
(図1-2で\(\omega t=2\pi\)のとき、\(t=T\)ですから、\(T=\frac{2\pi}{\omega}\)の関係があります。)
さて、単振動は円運動の正射影としてとらえることができることを使って、問題を解いてみます。
図1-3の右のように、P(の正射影)が\(x\)軸に沿って単振動をしているとき、PがP'からP"まで移動するのに要する時間を求めます。
単振動は、左の図の等速円運動の正射影と考えることができます。
したがって、P(の正射影)が\(x\)軸に沿ってP'からP"まで移動するのに要する時間は、
左の図で、Pが、中心角で\(\Delta\phi\)だけ、円運動する時間に等しいです。
そして、1回転に相当する\(2\pi\)の中心角が1周期\(T\)に対応するわけですから、求める時間を\(t\)として、
\(2\pi:T=\Delta\phi:t\)、ここで、\(\Delta\phi=\phi_2-\phi_1\)
として、求めることができます。
P'でのPの変位が\(\frac{1}{2}A\)で振幅の半分であることから、\(\phi_1=\frac{\pi}{6}\)、\(\phi_2=\frac{\pi}{2}\)です。
図1-3の右の図のように、P(の正射影)が線分上を単振動しているという図からは、
P(の正射影)がP'からP"まで移動する時間を求めるのは難しいですが、
図1-3の左の図のように、円運動を考えると、わかりやすくなります。
この問題は、下の図1-4の右の図のように、単振動の変位と時間の関係を表すグラフを考えても、解きやすくなります。
また、単振動の変位と時刻の関係を表す式\(x=A\sin \omega t\)がわかっているのであれば、
\begin{eqnarray}
\frac{1}{2}A&=&A\sin\omega t_1 \\
A&=&\sin\omega t_2 \\
もとめる時間&=&t_2-t_1
\end{eqnarray}
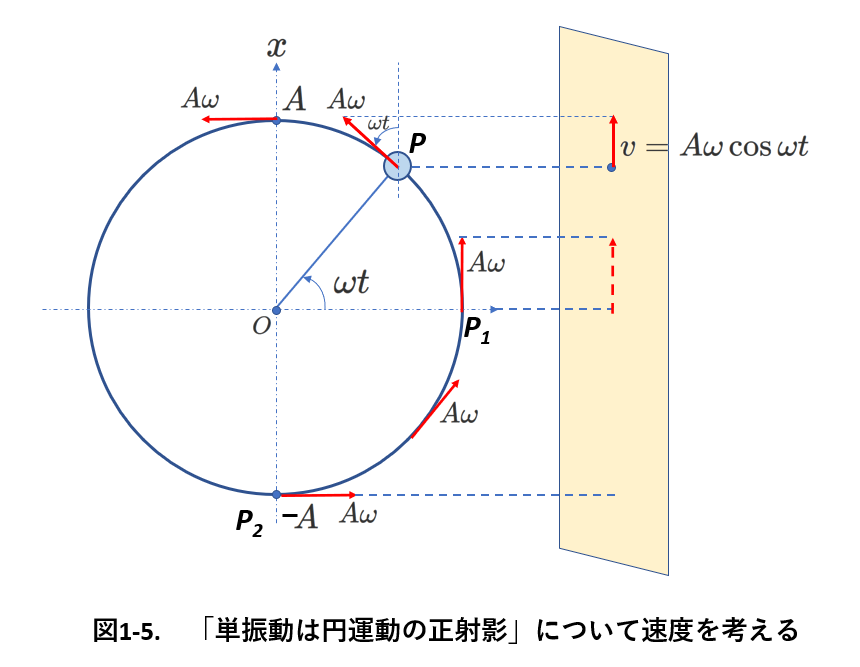
最後に円運動の正射影と単振動の速度について考えます。
図1-5を参照してください。
等速円運動ですから、どの瞬間でも円運動の速さは\(A\omega\)です。
ここで、円運動の各瞬間での速度ベクトルの右のスクリーンへの正射影が、Pの単振動の速度になります。
図からわかるように、正射影は\(A\omega\cos\omega t\)となり、(1-2)式に一致します。
また、図1-5から、
単振動の速度の大きさは、振動中心において最大となり、\(A\omega\)、
振動の上下端では、\(0\)となることが容易に理解できます。
Ⅱ.問題を解くためのツール
単振動の問題を解く上で主に使用できるものは、運動方程式・エネルギー保存則・運動量保存則、そして、単振動の性質などです。
1.運動方程式
単振動の運動方程式は、次の形に表されます。
\begin{eqnarray}
m\alpha&=&-k(x-x_0) \tag{2-1} \\
k&\gt& 0
\end{eqnarray}
ここで、\(\alpha\)は加速度、\(x\)は質量\(m\)の物体の座標、\(x_0\)は単振動の中心を表します。
運動方程式を立てて、それが(2-1)の式のように表されれば、運動は単振動であることを示したことになります。
その場合、\(k \gt 0\)の条件が必要です。
ばねにつながれたおもりの単振動では、\(k\)はばね定数に相当しますが、
\(k\)がばね定数でない場合も、(2-1)式が得られれば、質量\(m\)の物体は単振動をすることになります。
さらにこの式から、振動の中心\(x_0\)と角振動数\(\sqrt{\frac{k}{m}}\)がわかります。
単振動の運動方程式を、\(m\alpha=-kx+b\)のように表すこともできますが、
振動の中心がそのまま表されることから、(2-1)式を用いるほうが良いでしょう。
2.エネルギー保存則
単振動では、力学的エネルギーの保存を考える場合と、単振動のエネルギー保存を考える場合があります。
ふたつを比較すると、単振動のエネルギー保存を考えるほうが、計算が楽になることが多いです。
ただし、このふたつをしっかり区別して、計算の途中で混同することがないようにしましょう。
最初に、力学的エネルギーの保存を考えます。
図2-1のように、一方を壁に固定されたばねの他端に質量\(m\)の物体が取り付けられていて、単振動をしています。
水平方向に\(x\)軸を考え、図のように\(+x\)向きを定め、おもりが\(O\)の位置にあるときにばねは自然長にあるとします。
物体が座標\(x\)にあるときの速さを\(v\)、ばね定数を\(k\)として、力学的エネルギーの保存則を式で表せば、
\begin{equation} \frac{1}{2}kx^2+\frac{1}{2}mv^2=一定 \tag{2-2} \end{equation}
となります。
次に、図2-2のように、ばねの一端が天井に固定され、鉛直に吊るされたばねの他端に質量\(m\)のおもりが繋がっている場合を考えます。
この場合、おもりには振動方向に重力がはたらきます。
この場合の、力学的エネルギー保存の式は次のようになります。
\begin{equation} \frac{1}{2}kx^2+\frac{1}{2}mv^2-mg(x-h)=一定 \tag{2-3} \end{equation}
ここで、鉛直下向きが\(x\)方向の\(+\)の向きであること、位置エネルギーの基準を\(x=h\)にとっていることに注意してください。
この場合について運動方程式を立てると、加速度\(\alpha\)の正の向きを\(+x\)向きとして、
\begin{eqnarray} m\alpha&=&mg-kx \\
&=&-k(x-\frac{m}{k}g) \tag{2-4}
\end{eqnarray}
となります。
(2-4)式の意味を考えます。
図2-2の場合において、ばねの伸びは\(x\)で表されます。したがって、弾性力は\(-kx\)と表されるわけですが、
仮にばねの伸び量を\(x-\frac{m}{k}g\)と考えれば、重力の項を考慮しなくても運動方程式が立式できることを、(2-4)式は示しています。
ところで、\(x_0=\frac{m}{k}g\)は\(kx_0=mg\)と変形できることから、\(x_0\)は重力とばねの弾性力がつりあう位置を表しており、
\(x=x_0\)で\(\alpha=0\)となることから、\(x_0\)は振動の中心の座標であることがわかります。
以上のことから、力のつりあいの位置、あるいは、振動中心からのばねの伸縮量を考えた場合、重力の項を考慮する必要がないことがわかります。
このことは、エネルギー保存についても言えて、図2-2の場合にも重力の項を考えずに、
\begin{equation} \frac{1}{2}k(x-x_0)^2+\frac{1}{2}mv^2=一定 \tag{2-5} \end{equation}
と書くことができます。
(2-5)式が単振動のエネルギー保存の式となります。
第1項は単振動の位置エネルギー、第2項は運動エネルギーを表します。
つまり、
\begin{eqnarray} 「単振動のエネルギー」&=&「単振動の位置エネルギー」+「運動エネルギー」 \tag{2-6} \\
「単振動の位置エネルギー」&=&\frac{1}{2}k×[振動中心からの変位]^2 \tag{2-7}
\end{eqnarray}
となります。
さて、(2-3)式と(2-5)式の値は等しくないことに注意しましょう。
したがって、力学的エネルギーで考察する場合には力学的エネルギーで一貫して考察すること、
単振動のエネルギーを考えるのであれば、同じ式に力学的エネルギーを用いないことが大事です。
ここで、上記のこと、力学的エネルギーが保存されるのであれば単振動のエネルギーも保存されることを示します。
(2-5)式の左辺から考察を進めます。
\begin{eqnarray} \frac{1}{2}k(x-x_0)^2+\frac{1}{2}mv^2&=&\frac{1}{2}k(x-\frac{m}{k}g)^2+\frac{1}{2}mv^2 \\
&=&\frac{1}{2}kx^2-mgx+\frac{1}{2}kx_0^2+\frac{1}{2}mv^2 \\
&=&\left(\frac{1}{2}kx^2+\frac{1}{2}mv^2-mg(x-h)\right)+\left(\frac{1}{2}kx_0^2-mgh\right)
\end{eqnarray}
一つ目の括弧内の式は、(2-3)式と同じです。
また、二つ目の括弧内の式は、定数です。
したがって、(2-5)式が成り立てば、(2-3)式も成り立つことになり、(2-5)式と(2-3)式の値の差は、\(\frac{1}{2}kx_0^2-mgh\)であることがわかりました。
では、その差が\(0\)になるのはどういうときでしょうか。
\begin{eqnarray}
\frac{1}{2}kx_0^2-mgh&=&0 \\
h&=&\frac{1}{2}x_0
\end{eqnarray}
まとめると、力学的エネルギーの総和と単振動のエネルギーの総和は一般には一致しません。
それは、力学的エネルギーの総和を求めるときには重力による位置エネルギーの基準の取り方次第で力学的エネルギーの総和が変わってしまうためです。
位置エネルギーの基準を\(\frac{1}{2}x_0\)にとれば、力学的エネルギーの総和(2-3)式と単振動のエネルギーの総和(2-5)式の値が一致します。
3.運動量保存則
単振動している物体(おもり)の運動量は保存されません。
単振動では、位置に依存して速度の大きさも変化します。
このことから、運動量が保存されないことがわかります。
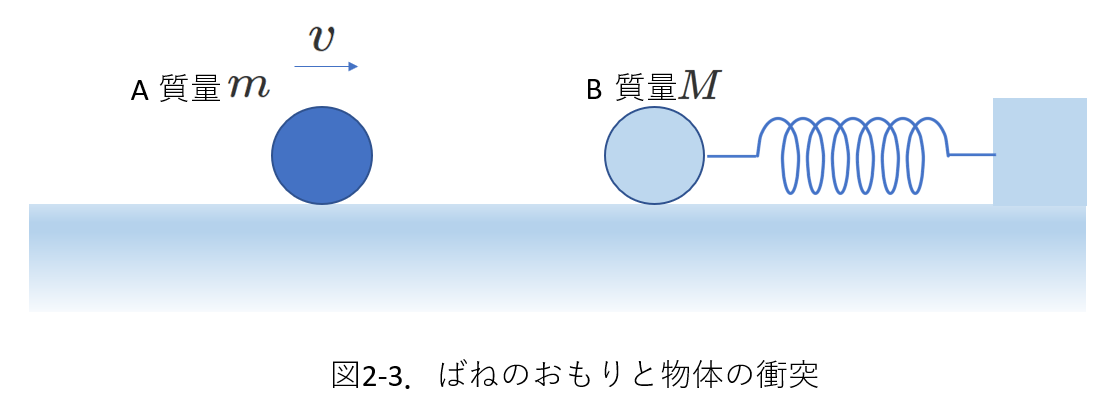
ここで、単振動に関連して運動量が保存されると考える例のひとつは、図2-3のような場合です。
右図は、一方を壁に固定されたばねの他端につながれたおもりBと物体Aが衝突する場面を表しています。
Bにはたらくばねの弾性力は、AとBからなる系に対して外力になりますから、厳密には、AとBからなる系の運動量の総和は衝突の前後で保存されません。
しかし、衝突に要する時間が非常に短いこと、衝突の衝撃によりAとBが及ぼし合う力は弾性力に比較して非常に大きいことから、近似的にこの衝突の直前直後で運動量が保存されると考えることができます。
4.単振動の運動の性質
「Ⅰ.単振動の運動の様子・・・加速度・速さ・位置の関係」の内容を考察に使う場合が多くあります。
この考え方には、慣れておく必要があります。
5.まとめ
以上の考えを整理して表します。
Ⅲ.運動方程式
1.単振動の運動方程式を立てる
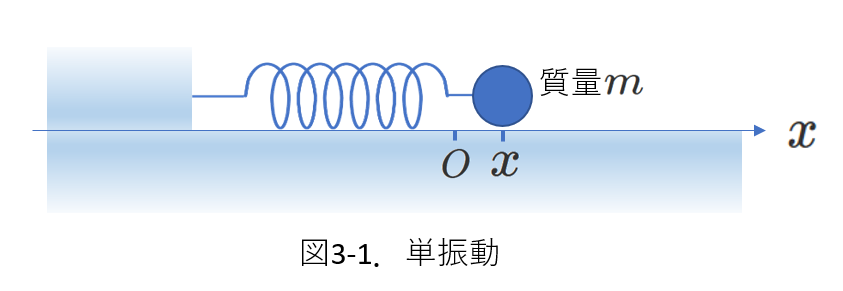
ばねの弾性力を\(F=kx\)と表すとき、\(x\)は座標(あるいは、変位)ですが、伸び(あるいは縮み)量も表していることに注意します。
さて、図3-1の場合について、ばねのおもりの運動方程式を立てます。
図のように\(x\)軸を決め、質量\(m\)のおもりが原点\(O\)にあるときにばねは自然長で、おもりが座標\(x\)にあるとき加速度が\(\alpha\)(\(+x\)向きが正)であるとして、運動方程式を立てると、
\begin{equation} m\alpha=-kx \tag{3-1} \end{equation}
となります。
おもりが図の位置にあるとき\(x \gt 0\)で、ばねは\(x\)だけ伸びていることになります。
これから、弾性力の大きさは\(kx\)でその向き(および、加速度の向き)は\(-x\)向きです。
注)運動方程式は、加速度と力の向きが同じであることを示しています。
次に、図3-2のように\(x \lt 0\)の場合に運動方程式を立て、(3-1)式と同じになることを確認します。
このとき、ばねは縮んでいます。
縮んだ量は、\(|x|=-x\)です。
したがって、ばねの弾性力の大きさは\(-kx(\gt 0)\)で、その向きは\(+x\)向きです。
つまり、この場合の運動方程式も(3-1)式と同じものになります。
2.単振動の運動方程式を立てる:重力が働く場合
次の図3-3について運動方程式を立てます。
図のように\(x\)軸を決め、質量\(m\)のおもりが原点にあるときにばねは自然長で、\(x=L\)でおもりに働く重力とばねの弾性力がつりあうものとします。
つまり、
\begin{eqnarray} kL=mg \tag{3-2} \\
L=\frac{mg}{k} \tag{3-3}
\end{eqnarray}
です。
次に、おもりが座標\(x\)にあるとき加速度が\(\alpha\)(\(+x\)向きが正)であるとして、運動方程式を立てます。
最初に、\(x \gt L\)の条件で運動方程式を立てます。
おもりに働く力は、図3-3に示すように重力(大きさ\(mg\))は下向き(\(+x\)向き)、弾性力は、大きさが\(kx(\gt 0)\)で向きは上向き(\(-x\)向き)ですから、運動方程式は、
\begin{eqnarray} m\alpha&=&-kx+mg \tag{3-4} \\
&=&-k\left(x-\frac{mg}{k}\right) \tag{3-5} \\
&=&-k(x-L) \tag{3-6}
\end{eqnarray}
となります。
次に、\(0 \lt x \lt L\)の領域で運動方程式を立てます。
この場合は、弾性力の大きさが図3-3の場合よりも小さくなる以外は、図3-3と同じです。
つまり、重力の大きさと向き、弾性力の向きは同じです。
したがって、運動方程式も図3-3の場合と同じになります。
\begin{equation} m\alpha=-kx+mg \tag{3-4}
\end{equation}
最後に、\(x \lt 0\)の領域で運動方程式を立ててみます。
この場合は、弾性力の大きさは\(-kx\)と表現され、向きは\(+x\)向きになります。
重力については図3-3、図3-4の場合と同じです。
したがって、運動方程式は次のようになります。図3-3、図3-4の場合と同じです。
\begin{equation} m\alpha=(-kx)+mg \tag{3-4}
\end{equation}
ここまで長く説明してきましたが、おもりが\(x\)の正の領域にあるとしても負の領域にあるとしても、立てた運動方程式は同じになります。そして、運動方程式は、おもりが\(x\)の正の領域にあると仮定して立てるのがわかりやすいこともわかります。
3.単振動の運動方程式の形から振動中心と角振動数を求める
単振動の運動方程式からわかることをまとめておきます。
(3-4)(3-5)式をここにもう一度記述します。
\begin{eqnarray} m\alpha&=&-kx+mg \tag{3-4} \\
&=&-k\left(x-\frac{mg}{k}\right) \tag{3-5} \\
\end{eqnarray}
①運動方程式を立てたときに(3-4)(3-5)式のように表されれば、その運動は単振動です。
大事なことは、\(x\)の係数が負であることです。
負であれば、\(x\)が正のとき、加速度は\(-x\)向き、\(x\)が負のとき加速度は\(+x\)向きとなり、
おもりにはたらいている力は復元力で、運動は単振動であるとわかります。
②振動中心の座標
(3-5)式から\(x=\frac{mg}{k}\)が振動中心であることがわかります。
振動中心では、加速度は\(0\)ですから、(3-4)式、または、(3-5)式に\(\alpha=0\)を代入すれば\(x=\frac{mg}{k}\)が得られます。
もうひとつの考え方は、振動中心ではおもりにはたらく力はつりあっていることから、(3-4)式の右辺が\(0\)に等しいと考えることです。
(3-4)式を立式したとき、(3-5)式の形に変形しておくと、振動中心がわかりやすくなります。
③角振動数
運動方程式が(3-4)式、または、(3-5)式で表されるとき、単振動の角振動数\(\omega\)は、\(\omega=\sqrt{\frac{k}{m}}\)となります。
おもりが単振動しているとき、そのおもりの加速度\(\alpha\)は\(\omega\)を用いて表すことができて、\(\alpha=-\omega^2 (x-x_0)\)となります。(\(x_0\)は振動中心の座標) つまり、
\begin{eqnarray} m\alpha&=&-m\omega^2(x-x_0) \tag{3-6} \\
m\alpha&=&-kx+mg=-k\left(x-\frac{mg}{k}\right) \tag{3-4}
\end{eqnarray}
と、2つの表現の運動方程式が立式できて、(3-6)式と(3-4)式を比較することで、\(\omega\)(および、\(x_0\))が求められます。
【参考】
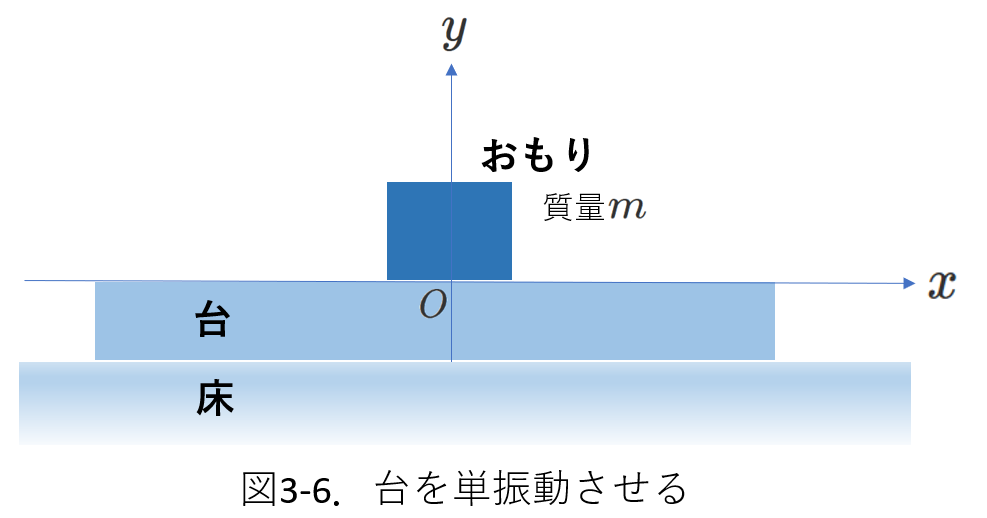
単振動の加速度\(\alpha\)を\(\alpha=-\omega^2 (x-x_0)\)と表すことを使って、問題を解く場合があります。
図3-6で平板の台の上に直方体のおもりが乗っています。そして、台は床に支えられています。
台とおもりの間には摩擦が存在しますが、台と床の間には摩擦はないものとします。
今、台に力をはたらかせて、原点\(O\)を中心として振幅\(B\)、角振動数\(\omega\)で左右方向に、台を単振動させます。
時刻\(t=0\)でおもりは\(x=-B\)にあるとします。
おもりが台上をすべることがなかったとして、おもりと台の間にはたらいている静止摩擦力を求めます。
問題を解く準備として、
台の座標を\(X\)、速度を\(V\)、加速度を\(A\)とします。
上に掲げた条件から、
\begin{equation} X=-B\cos\omega t \tag{3-7} \end{equation}
これより、
\begin{eqnarray} V&=&\frac{dX}{dt}=B\omega \sin\omega t \tag{3-8} \\
A&=&\frac{dV}{dt}=B\omega^2 \cos\omega t \tag{3-9}
\end{eqnarray}
さて、この問題でも、最初に行うことはおもりにはたらく力(および、台にはたらく力)を図に表すことです。
その場合、ふたつの立場があります。
①台の上(の人)から運動を観察する場合
②おもりと台からなる系の外から運動を観察する場合
①の場合、
おもりは台の上を滑ることなく、台と一緒に運動するわけですから、台上の人から見ると、おもりは止まっているように見えます。
つまり、おもりにはたらく力はつりあっています。
そして、このとき、おもりに左右方向(つまり運動の方向)にはたらく力は図3-7に示すように、摩擦力\(f\)と慣性力\(F\)です。
鉛直方向には重力と抗力がはたらいていますが、それらはつりあっていて鉛直方向におもりは運動をしていません。
台は加速度運動(単振動)をしていますから、おもりには慣性力がはたらきます。
(3-9)式から、台の加速度は\(B\omega^2 \cos\omega t\)ですから、慣性力は\(-mB\omega^2 \cos\omega t\)です。
負号は、台の加速度とは逆向きに力がはたらくことを意味しています。
台は単振動をしているので、加速度も時間により大きさと向きが変わります。
したがって、おもりにはたらく慣性力も大きさと向きが変わります。
符号に十分注意して式を立てる必要があります。
向きが変わる力を図示ときは、力の向きをどちらに向けて描いてよいか迷います。
ある特定の時刻を仮定して、そのときの図を描くようにします。
図3-7では、\(t=0\)を想定して描いています。
\(t=0\)では、台は最も左端にあり、台の加速度は右向きで大きさは最大です。
このことから、おもりにはたらく慣性力は左向き、それとつり合う摩擦力は右向きであることがわかります。
さて、図3-7にしたっがて、\(f=F\)という式を立てる場合、慣性力\(F\)は左向きが正であると考えています。
一方で、慣性力を\(-mB\omega^2 \cos\omega t\)と表現した場合、慣性力は右向きを正としています。
この負号の扱いに注意して、
慣性力を\(-mB\omega^2 \cos\omega t\)と表現してつりあいの式を立てる場合は、
\begin{eqnarray} f+(-mB\omega^2 \cos\omega t)&=&0 \tag{3-10} \\
f&=&mB\omega^2 \cos\omega t \tag{3-11}
\end{eqnarray}
とします。
摩擦力は右向きを正と設定しているので、(3-10)式に従えば、\(t=0\)で\(f\gt 0\)で、摩擦力は最初は右向きにはたらくことになり、これは問題の条件に合っています。
また、図3-7から、\(f=F\)と立式する場合には、\(F\)は左向きが正ですから、\(F=mB\omega^2 \cos\omega t\)と考えて、式を立てます。
これは、\(t=0\)近傍での台の加速度の大きさが\(B\omega^2 \cos\omega t\)ですから、慣性力の大きさは\(mB\omega^2 \cos\omega t\)で向きは左向きと、考えていることになります。
次に②の場合は、
系の外からおもりの運動を見たとき、おもりは(台と一緒に)単振動をしているように見えます。
おもりが単振動をしているということは、おもりに復元力が働いていることです。
おもりにはたらく力を考えると、図3-8のようになります。
おもりに左右方向にはたらく力は摩擦力だけです。つまり、摩擦力が復元力です。
この摩擦力により、おもりは角振動数\(\omega\)、振幅\(B\)の単振動をします。つまり、おもりが受ける加速度は(3-9)式で表されます。
摩擦力\(f\)により、おもりが(3-9)式で表される加速度を受けることを、運動方程式に表せば、
\begin{equation} m\times B\omega^2 \cos\omega t=f \end{equation}
となります。(3-11)式と同じ結果になりました。
ところで、図3-8で\(f'\)は台を振動させている力です。
台には、おもりとの間の摩擦力\(f\)もはたらくので、台の質量を\(M\)として、台についての運動方程式を立てれば
\begin{eqnarray} M\times B\omega^2 \cos\omega t&=&f'-f \\
f'&=&MB\omega^2 \cos\omega t+f \\
&=& MB\omega^2 \cos\omega t+ mB\omega^2 \cos\omega t \\
&=&(M+m)B\omega^2 \cos\omega t \tag{3-12}
\end{eqnarray}
となります。
(3-12)式から、\(f'\)は、おもりと台の両方を角振動数\(\omega\)、振幅\(B\)で振動させていることが読み取れます。
Ⅳ.エネルギー保存則
単振動のエネルギー保存では、ふたつの考え方があります。
「力学的エネルギー保存」と「単振動のエネルギー保存」です。
「Ⅱ.問題を解くためのツール」では、図2-2を元に次のふたつのエネルギー保存の式を立てました。
この場合の、力学的エネルギー保存の式は次のようになります。
\begin{equation} \frac{1}{2}kx^2+\frac{1}{2}mv^2-mg(x-h)=一定 \tag{2-3} \end{equation}
\(h\)は位置エネルギーの基準です。
また、単振動のエネルギー保存の式は次のように表されます。
\begin{equation} \frac{1}{2}k(x-x_0)^2+\frac{1}{2}mv^2=一定 \tag{2-5} \end{equation}
ここで、\(x_0\)は振動の中心の座標です。
(2-5)式からわかるように、重力がはたらく場合でもつり合いの位置からの変位\((x-x_0)\)を考える単振動のエネルギー保存の式では、エネルギー保存の式に、重力による位置エネルギーの項を含めなくてよくなります。
では、図2-2の構成で、おもりを\(x=L (L\gt 0) \)の位置まで伸ばし、静かに手を放したときのおもりの振動範囲を求めてみましょう。
ばねは\(x=0\)で自然長として、伸びが\(L\)であることになります。
【参考】
図2-2のおもりの運動が単振動であることはわかります。
振動中心\(x_0\)では、ばねの弾性力\(kx_0\)(上向き)と重力\(mg\)(下向き)がつりあうことから、\(x_0\)が求められます。
\begin{eqnarray} kx_0&=&mg \\
x_0&=&\frac{mg}{k} \tag{4-1}
\end{eqnarray}
\(x=L\)でおもりを静かに放すということは、その点で速度が\(0\)ということですから、\(x=L\)は振動の下端であることになります。(\(x\)軸が下向き正であることに注意)
このことから、振幅\(B\)は\(L-x_0\)となります。
したがって、上端は\(x_0-B=2x_0-L\)です。
以上より振動範囲は、
\begin{eqnarray} 2x_0-L \lt &x& \lt L \\
\frac{2mg}{k}-L \lt &x& \lt L \tag{4-2}
\end{eqnarray}
検算しておきましょう。
上端と下端の座標の中心は振動中心ですから、「\(\frac{上端+下端}{2}=振動中心\)」となるはずで、実際そのようになっています。
次に、【力学的エネルギーの保存】を用いてこの問題を解いてみましょう。
重力による位置エネルギーの基準を\(x=0\)として、
[手を放す瞬間の力学的エネルギー]=[座標\(x\)で速度が\(v\)のときの力学的エネルギー]と、表すことにします。
式に表せば、
\begin{equation} \frac{1}{2}kL^2+\frac{1}{2}m\times 0^2+(-mgL)=\frac{1}{2}kx^2+\frac{1}{2}mv^2+(-mgx) \tag{4-3} \end{equation}
単振動でおもりが存在しうる\(x\)を求めるには、存在しうる地点では\(v\gt 0\)、または、\(v^2\gt 0\)(言い換えれば、\(v\)は実数)という条件を使います。
(4-3)から、
\begin{eqnarray} \frac{1}{2}mv^2=\frac{1}{2}kL^2-\frac{1}{2}kx^2-mgL+mgx \\
\frac{1}{2}mv^2 \gt 0 として、\\
\frac{1}{2}kL^2-\frac{1}{2}kx^2-mgL+mgx \gt 0 \\
mg(x-L)-\frac{1}{2}k(x-L)(x+L) \gt 0 \\
(x-L)\left(mg-\frac{1}{2}k(x+L)\right) \gt 0 \\
-\frac{1}{2}k(x-L)\left(x+L-\frac{2mg}{k}\right) \gt 0
\end{eqnarray}
これより、
\begin{equation} \frac{2mg}{k}-L \lt x \lt L \end{equation}
となり、(4-2)式と一致しました。
では、【単振動のエネルギーの保存】を用いてこの問題を解いてみましょう。
この場合には、
[手を放す瞬間の単振動のエネルギー]=[座標\(x\)で速度が\(v\)のときの単振動のエネルギー]と、表します。
式を立てれば、
\begin{equation} \frac{1}{2}k(L-x_0)^2+\frac{1}{2}m\times 0^2=\frac{1}{2}k(x-x_0)^2+\frac{1}{2}mv^2 \tag{4-4} \end{equation}
単振動でおもりが存在しうる\(x\)を求めるには、存在しうる地点では\(v\gt 0\)、または、\(v^2\gt 0\)(言い換えれば、\(v\)は実数)という条件を使います。
(4-4)から、
\begin{eqnarray} \frac{1}{2}mv^2=\frac{1}{2}k(L-x_0)^2-\frac{1}{2}k(x-x_0)^2 \\
\frac{1}{2}mv^2 \gt 0 として、\\
\frac{1}{2}k(L-x_0)^2-\frac{1}{2}k(x-x_0)^2 \gt 0 \\
\frac{1}{2}k(L-x_0+x-x_0)(L-x_0-x+x_0) \gt 0 \\
-\frac{1}{2}k(x+L-2x_0)(x-L) \gt 0
\end{eqnarray}
これより、
\begin{equation} 2x_0-L \lt x \lt L \end{equation}
となり、こちらも(4-2)式と一致しました。
単振動のエネルギー保存を使うほうが計算は楽のようですが、単振動のエネルギー保存を使うには振動の中心\(x_0\)を求める必要があります。
一方、力学的エネルギーの保存を使う場合は、振動の中心がわからなくても、答えが求められます。
見方を変えれば、力学的エネルギーの保存の式から求めた範囲から振動の中心を求めることができます。
上の例題では、【参考】に書いたように、振動の性質を使うことで答えを得ることができ、エネルギー保存を用いるメリットはあまりないようです。
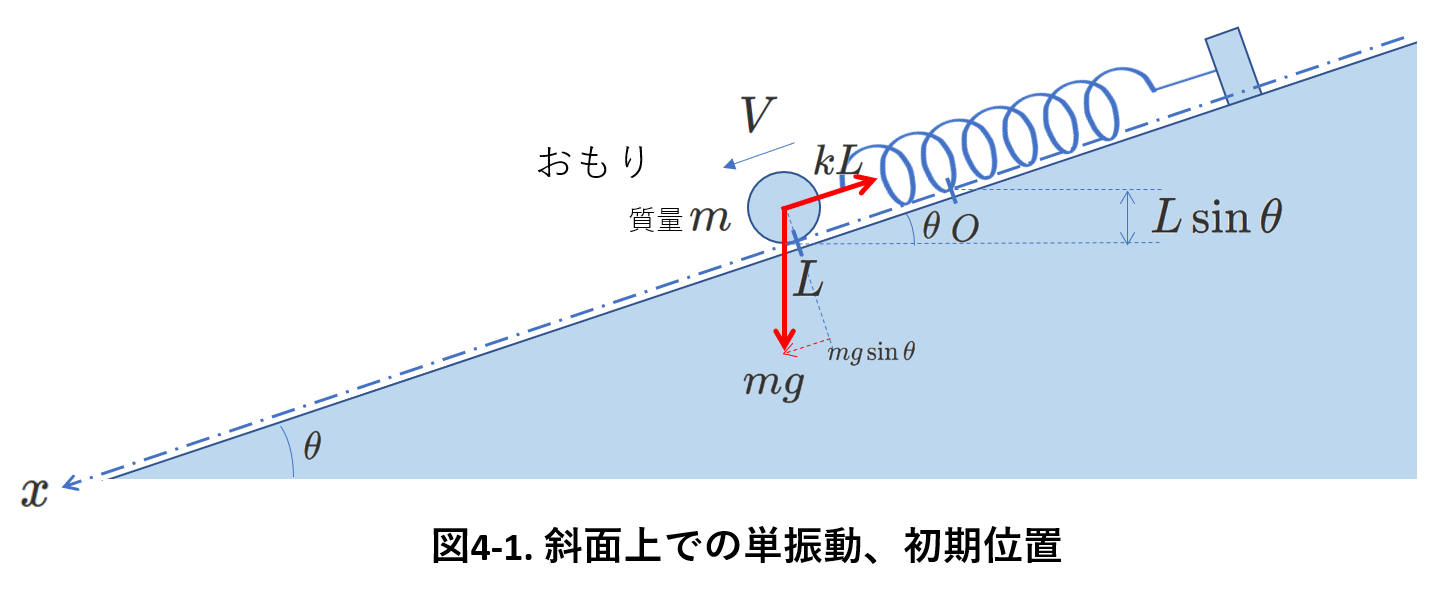
そこで、エネルギー保存が効果を発揮する次の図4-1の例題を考えます。
角度\(\theta\)の斜面にばね(ばね定数\(k\))の一端が固定されています。
図のように他端に質量\(m\)のおもりを取り付けて、おもりが振動できるようにしています。
斜面に沿った\(x\)軸を考え、下向きを\(+x\)向きとします。
また、おもりが原点\(O\)(\(x=0\))にあるとき、ばねは自然長であるとします。
図4-1のように、\(x=L\)でおもりの速度が\(V\)であったとき、おもりの存在する\(x\)の範囲を求めます。
力学的エネルギーを考えます。
図4-1の状態の力学的エネルギーは、位置エネルギーの基準を\(x=0\)にとって、
\begin{equation} \frac{1}{2}kL^2+\frac{1}{2}mV^2+(-mgL\sin\theta) \end{equation}
と表されます。
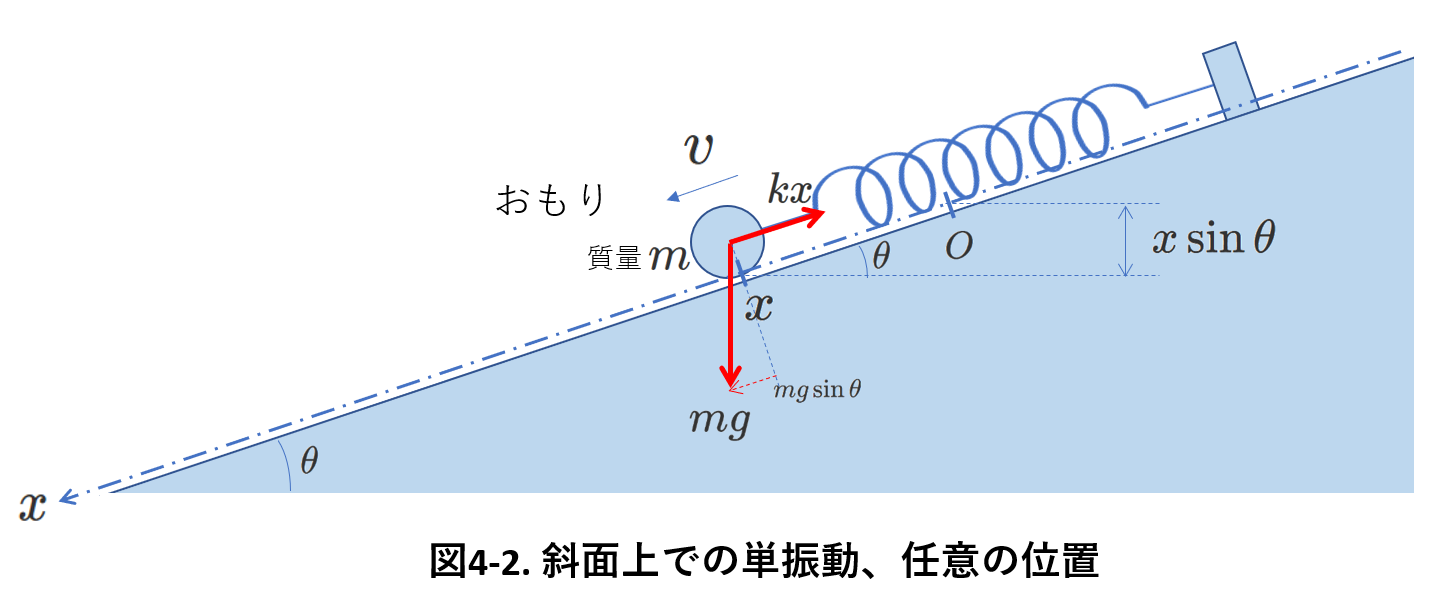
おもりの存在する\(x\)の範囲を求めるため、図4-2のように、任意の位置\(x\)での力学的エネルギーを考えます。
このときのおもりの速度を\(v\)として、力学的エネルギーは、
\begin{equation} \frac{1}{2}kx^2+\frac{1}{2}mv^2+(-mgx\sin\theta) \end{equation}
です。
以上より、力学的エネルギー保存の式は、つぎのようになります。
\begin{equation} \frac{1}{2}kL^2+\frac{1}{2}mV^2+(-mgL\sin\theta)=\frac{1}{2}kx^2+\frac{1}{2}mv^2+(-mgx\sin\theta) \tag{4-5} \end{equation}
上の式は\(x\)の2次方程式で解くのにてこずります。
そこで、たいてい特殊な場合を想定して(4-5)式を解くことになります。
ここでは、
\begin{eqnarray} \theta&=&\frac{\pi}{6} \\
V&=&\frac{1}{2}\sqrt{gx_0} \\
L&=&2x_0
\end{eqnarray}
という条件で計算してみましょう。
ここで、\(x_0\)は振動の中心です。
振動の中心では、重力とばねによる弾性力の斜面方向成分がつりあっているので、
\begin{eqnarray} mg\sin\theta&=&kx_0 \tag{4-6} \\
x_0&=&\frac{mg\sin\theta}{k} \tag{4-7}
\end{eqnarray}
(4-5)式を変形して、
\begin{eqnarray} \frac{1}{2}mv^2=\frac{1}{2}kL^2+\frac{1}{2}mV^2-mgL\sin\theta-\frac{1}{2}kx^2+mgx\sin\theta \\
おもりが存在しうる範囲は、\frac{1}{2}mv^2 \geqq 0 から求めることができるので、 \\
\frac{1}{2}kL^2+\frac{1}{2}mV^2-mgL\sin\theta-\frac{1}{2}kx^2+mgx\sin\theta \geqq 0 \\
-\frac{1}{2}kx^2+mg\sin\theta \times x+\frac{1}{2}kL^2+\frac{1}{2}mV^2-mgL\sin\theta \geqq 0 \tag{4-8} \\
上の条件とmg\sin\theta=kx_0(つりあいの式)を使って、 \\
-\frac{1}{2}kx^2+kx_0\times x+\frac{1}{2}k\times 4x_0^2+\frac{1}{2}\frac{1}{4}\frac{kx_0}{\sin\theta}x_0-kx_0\times 2x_0 \geqq 0 \\
-\frac{1}{2}kx^2+kx_0x+\frac{1}{4}kx_0 \geqq 0 \\
x=\left(1+\frac{\sqrt{6}}{2}\right)x_0、\left(1-\frac{\sqrt{6}}{2}\right)x_0 \\
つまり、xの範囲は、 \\
\left(1-\frac{\sqrt{6}}{2}\right)x_0 \leqq x \leqq =\left(1+\frac{\sqrt{6}}{2}\right)x_0 \tag{4-9}
\end{eqnarray}
となります。
次に、単振動のエネルギー保存を使って考えます。
単振動のエネルギーの保存を表す式は、次のようになります。
\begin{equation} \frac{1}{2}k(L-x_0)^2+\frac{1}{2}mV^2=\frac{1}{2}k(x-x_0)^2+\frac{1}{2}mv^2 \tag{4-10} \end{equation}
おもりが存在しうる範囲は、\(\frac{1}{2}mv^2 \geqq 0\) から求めることができるので、
\begin{equation} \frac{1}{2}k(L-x_0)^2-\frac{1}{2}k(x-x_0)^2+\frac{1}{2}mV^2 \geqq 0 \tag{4-11} \end{equation}
を解くことになります。
計算すれば、(4-9)式と同じ結果が得られます。
【参考】
単振動の振幅を\(A\)(\(A\gt 0\))、振動の中心の座標を\(x_0\)とすれば、
おもりの存在する\(x\)の範囲は、\(x_0-A \leqq x \leqq x_0+A\)と表されます。
振動の端(上端、下端)では、速度が\(0\)となることを考慮して、単振動のエネルギーの保存式を立てれば、
\begin{equation} \frac{1}{2}k(L-x_0)^2+\frac{1}{2}mV^2=\frac{1}{2}kA^2 \tag{4-12} \end{equation}
この式は、(4-10)式において、\(v=0\)を代入した形で、この式を解くということは、(4-11)式の等号が成立する場合について解くと同じであることに注意してください。
(4-12)式は左辺が定数ですから、\(A\)を求める計算は楽です。このことを覚えておきましょう。
\(\theta\)、\(V\)、\(L\)の条件を入れて、(4-12)式を解くと、
\begin{eqnarray} A^2&=&(L-x_0)^2+\frac{m}{k}V^2 \\
A&=&\sqrt{(L-x_0)^2+\frac{m}{k}V^2} \\
&=&\sqrt{(2x_0-x_0)^2+\frac{m}{k}\left(\frac{1}{2}gx_0 \right)^2} \\
&=&\sqrt{x_0^2+\frac{x_0}{g\sin\theta}\frac{1}{4}\sqrt{gx_0}} \\
&=&\sqrt{x_0^2+2x_0\frac{1}{4}x_0} \\
&=&x_0\sqrt{1+\frac{1}{2}} \\
&=&\frac{\sqrt{6}}{2}x_0
\end{eqnarray}
この\(A\)の値を使って、\(x_0-A \geqq x \geqq x_0+A\)を考えれば、(4-9)式と同じ結果が得られます。
Ⅴ.運動量の保存則
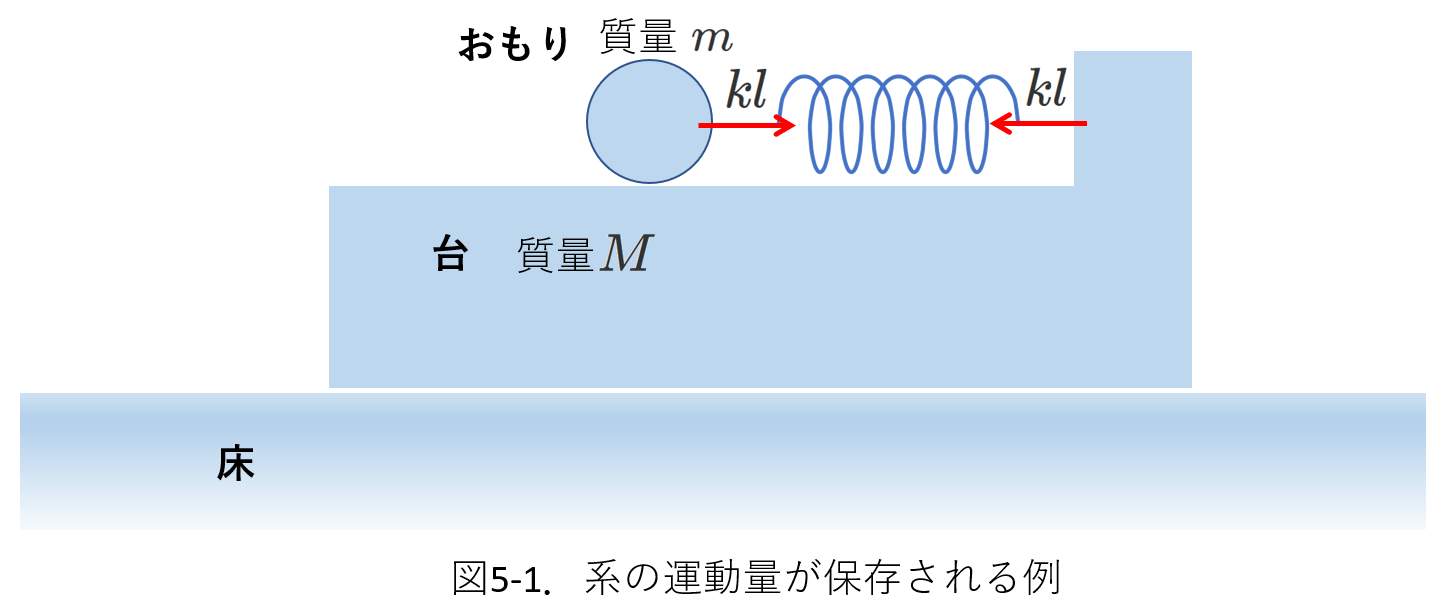
1.系の運動量が保存される場合
右図5-1で、おもりと台からなる系の運動量は保存されます。
床の上に台が置かれ、その台の上におもりが置かれています。
おもりと台はばね定数が\(k\)のばねでつながれています。
おもりと台の間、および、台と床の間に摩擦はないものとします。
今、初期状態でおもりも台も(床に対して)静止していて、\(t=0\)の時刻におもりに右向きの速度\(v_0\)を与えます。
このとき、台から見ておもりは単振動をします。
図5-1の状態で、おもりにも台にも重力がはたらきますが、おもりと台が及ぼし合う垂直抗力、および、台と床が及ぼし合う垂直抗力とつりあっていて、鉛直方向には運動をしません。
左右方向には、おもりにも台にもばねの弾性力(大きさ\(kl\))がはたらきます。ここで、\(l\) はばねの伸縮量を表します。
この弾性力により単振動の運動をします。
さて、この弾性力は、おもりにも台にもはたらき、その大きさは等しく向きは逆向きです。
したがって、おもりと台からなる系を考えると、ばねの弾性力は内力になります。
このため、おもりと台からなる系の運動量は保存されます。
前述したように、おもりと台は初期には静止していて、\(t=0\)でおもりに\(v_0\)の初速を与えます。
その後、任意の時間でのおもりの速度を\(v\)、台の速度を\(V\)として、右向きを正の向きとして、運動量保存則を立てると、
\begin{equation} mv_0=mv+MV \tag{5-1} \end{equation}
となります。
さて、図5-1は複雑な系のように思われますが、おもりと台の間に摩擦がないため、次の図5-2と類似の設定です。
(おもりA,Bと床の間には摩擦はないものとします。)
内力だけがはたらく系では系の重心は静止しているか、等速度運動をします。
これを運動量保存から導いてみます。
図5-2のおもりAとおもりBからなる系において、運動量保存を表す式は、
\begin{equation} mv+MV=一定=P \tag{5-2} \end{equation}
運動量の一定値を\(P\)としました。
さて、AとBの重心の座標を\(x_G\)、重心の速度を\(v_G\)とすると、
\begin{eqnarray} x_G&=&\frac{mx+MX}{m+M} \tag{5-3} \\
v_G&=&\frac{dx_G}{dt}=\frac{m\frac{dx}{dt}+M\frac{dX}{dt}}{m+M} \\
&=&\frac{mv+MV}{m+M} \tag{5-4} \\
&=&\frac{P}{m+M}=一定
\end{eqnarray}
となります。
このように、\(v_G=一定\)ですから、重心は静止(\(v_G=0\))、または、等速度運動(\(v_G\neq 0\))をしていることがわかります。
次にAとBについて運動方程式を立てて、Bから見たAの運動(単振動)の角振動数を求めます。
このような問題の常套手段は、それぞれのおもりの座標と速度を仮定して、それをもとに運動方程式を立てます。
また、ばねの自然長を\(l\)とすれば、ばねの伸びは、\(X-x-l\)となるので、弾性力は\(k(X-x-l)\)です。
以上より、加速度、速度の正の向きを\(+x\)向きとし、
おもりAとBの加速度をそれぞれ、\(a\)、\(A\)とすれば、運動方程式は、
\begin{eqnarray} Aについて、ma&=&k(X-x-l) \tag{5-5} \\
Bについて、MA&=&-k(X-x-l) \tag{5-6}
\end{eqnarray}
さて、Bから見たAの加速度は\(a-A\)、座標は\(x-X\)ですから、
(5-5)式×M-(5-6)式×mを計算します。
\begin{eqnarray} mM(a-A)&=&(m+M)k(X-x-l) \\
&=&-(m+M)k\{(x-X)+l\} \tag{5-7}
\end{eqnarray}
この式は、おもりBから見たAの運動が、\(l\)離れた点(つまりばねの自然長の位置)を中心とした単振動であることを示しています。
\(x-X\)の係数が負であることが単振動の必要条件ですから、常に座標の係数の正負に注意しましょう。
角振動数\(\omega\)は、
\begin{equation} \omega=\sqrt{\frac{(m+M)k}{mM}} \tag{5-8} \end{equation}
です。
この答えを検証してみます。
仮に、おもりBの質量が非常に大きい場合、Bはほとんど静止した状態になりますから、ばねのB側が固定された状態のAの単振動と同じになるはずです。そこで、(5-8)式の分母分子を\(M\)で割って、\(M\to\infty\)の極限を考えます。
\begin{eqnarray} \omega&=&\sqrt{\frac{(m+M)k}{mM}} \\
&=&\sqrt{\frac{\left(\frac{m}{M}+1\right)k}{m}}
\end{eqnarray}
ここで、、\(M\to\infty\)とすれば、
\begin{equation} \omega=\sqrt{\frac{k}{m}} \tag{5-9} \end{equation}
【慣性力を考える】
Bから見たAの加速度を求める場合、Bは加速度運動をしているのですから、Aには慣性力がはたらくはずだと、考えるかもしれません。この立場で問題を考えてみましょう。
Bの加速度\(A\)は(5-5)式から求められます。
これにより、Aにはたらく慣性力は向きが加速度\(A\)の逆向きですから、慣性力は\(-mA\)で与えられます。
Bから見たAの加速度は\(a-A\)であることに注意して、Bから見たAの運動方程式を立てます。
\begin{eqnarray} m(a-A)&=&-mA+k(X-x-l) \\
&=&m\times \frac{k}{M}(X-x-l)+k(X-x-l) \\
mM(a-A)&=&(m+M)k(X-x-l)
\end{eqnarray}
となり、(5-7)式と一致しました。
つまり、相対加速度を計算することと慣性力を考えることは視点は異なりますが、同じ結果が得られます。
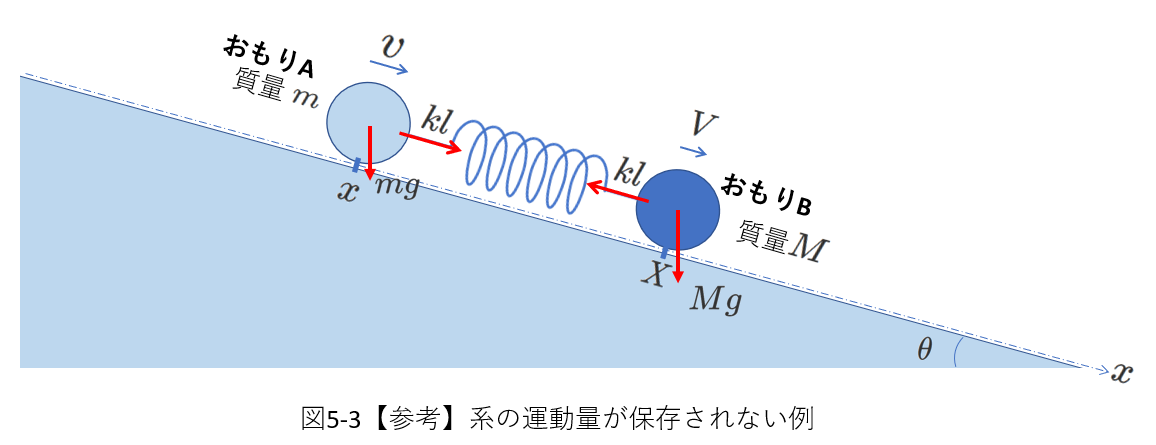
比較のため、 図5-2のおもりA、Bとばねからなる系を斜面においてみましょう。これを、図5-3に示しました。
この状態でAとBはどのような運動をするのでしょう。
大事なことは、斜面に置かれたAとBからなる系の運動量は保存されないということです。
なぜなら、おもりAにもおもりBにも運動する方向(斜面に沿った方向)に、重力の斜面方向の成分がはたらいています。
これは、AとBからなる系にとって外力になります。AとBは重力の斜面方向成分によりが同じ向きに加速され、速度を増します。したがって、もはや運動量は保存されません。
図5-2に関連して、運動量保存則が成り立つような内力だけがはたらいている系では、系の重心は静止しているか、等速度運動をしているということでしたが、図5-3の例では、外力がはたらいていて、運動量保存則が成立しないわけですから、重心はこれとは異なる運動をすることが予想できます。
図5-3の運動を理解するため、
①Bから見たAの運動(Bから見たAの加速度(相対加速度))
②AとBの重心の加速度
を調べます。
最初に、おもりAとBについて、運動方程式を立てます。
おもりAの加速度を\(a\)、Bの加速度を\(A\)として、加速度の正の向きを\(x\)軸の正の向きとします。
ばねの自然長を\(l\)とすれば、図5-2の議論と同様にして、
\begin{eqnarray}
A:ma&=&k(X-x-l)+mg\sin\theta \tag{5-10} \\
B:MA&=&-k(X-x-l)+Mg\sin\theta \tag{5-11}
\end{eqnarray}
①については、\(a-A\)を求めることになるので、(5-10)式×\(M\)-(5-11)式×\(m\)を計算します。
\begin{eqnarray} mM(a-A)&=&(m+M)k(X-x-l)+Mmg\sin\theta-mMg\sin\theta \\
&=&(m+M)k(X-x-l) \\
&=&-(m+M)k\{(x-X)+l\}
\end{eqnarray}
この式は(5-7)式と同じですから、BからAを見た運動は単振動でその角振動数は(5-9)式で与えられるということがわかります。
②については、重心の加速度\(a_G\)を計算してみます。
(5-4)式をもう一度微分すれば、\(a_G\)が得られますから、\(a_G\)は次のように計算できます。
\begin{eqnarray} a_G&=&\frac{m\frac{dv}{dt}+M\frac{dV}{dt}}{m+M} \\
&=&\frac{ma+MA}{m+M} \tag{5-12}
\end{eqnarray}
この式の分子が(5-10)式と(5-11)式の和であることがわかれば、\(a_G\)は簡単に計算できて、
\begin{eqnarray} a_G&=&\frac{mg\sin\theta+Mg\sin\theta}{m+M} \\
&=&\frac{(m+M)g\sin\theta}{m+M} \\
&=&g\sin\theta
\end{eqnarray}
つまり重心は、加速度が\(g\sin\theta\)の等加速度運動をすることがわかります。
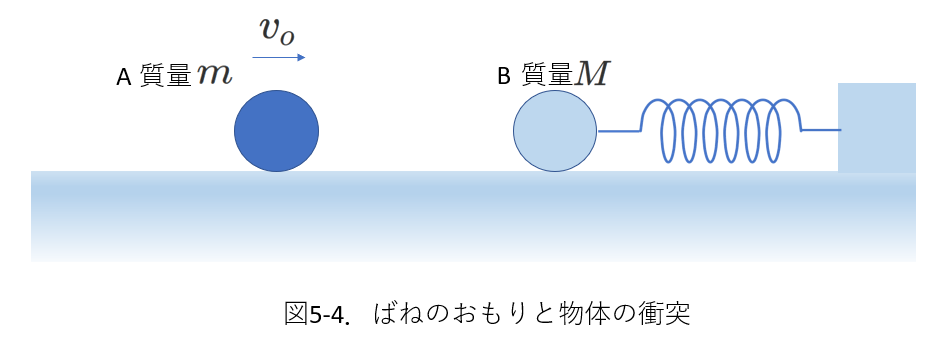
2.おもりと物体の衝突
右図5-4のような、ばねにつながれたおもりに別の物体が衝突するという問題は比較的多いです。
図では、静止している質量\(M\)のおもりBに、質量\(m\)で速度が\(v_0\)の物体Aが衝突します。
衝突により、最初静止していたBは、衝突直後にある速度\(V\)を持つことになります。その後、AはBの運動を妨げないとして、Bは単振動をします。
つまり、Bにはたらく力の合力が\(0\)の位置(すなわち、振動の中心)で速度\(V\)を持つことになり、その場合の単振動はどのような単振動なのか、という問題になります。
さて、\(V\)を求めるには、運動量保存則を持ちいるわけですが、この場合、厳密には運動量は保存されません。
Bが静止しているのであれば、弾性力ははたらかず、運動量は保存されますが、
実際には、衝突時のAとBの力の及ぼし合いはある時間続くわけですから、その間にBがわずかに移動して外力であるばねによる弾性力がはたらき、運動量が保存される条件が崩れてしまいます。
しかし、このような問題では、弾性力の影響は小さいと考えて運動量は保存されると考えて問題を解くのが通例です。
これは、衝突の極めて短い時間の間にそれぞれの物体の速度が変化するほど大きな力が作用するのですから、衝突による力は外力(弾性力)に比べて非常に大きいと考えられるからです。
問題に、「外力の影響は無視できる」などの断り書きがある場合もありますが、ない場合もあるので、問題文をよく検討して、運動量保存が使えるか否かを判断しましょう。
さて、図5-4の場合、衝突直後のAとBの速度をそれぞれ\(v\)、\(V\)として、運動量保存の式を立てれば、
\begin{equation} mv_0=mv+MV \tag{5-13} \end{equation}
となります。
上式では\(v\)も未知数ですから、\(V\)を決定するにはもうひとつの条件が必要になります。
たいていの場合、どんな衝突であるか(弾性衝突、完全非弾性衝突、はねかえり係数の値)を見極めて\(V\)を決めることになります。
以下の表に、衝突の種類を分類します。
| 衝突の種類 | 完全非弾性衝突 | 非弾性衝突 | 弾性衝突 |
|---|---|---|---|
| 反発係数(はね返り係数)\(e\) | \(e=0\) | \(0\leqq e \lt 1\) 1) | \(e=1\) |
| \(V\)を求めるための条件 | \begin{equation} 0=-\frac{v-V}{v_0-0} \end{equation}したがって、\(v=V\) | \(e\)が与えられていれば、\begin{equation} e=-\frac{v-V}{v_0-0} \end{equation} | \begin{equation} 1=-\frac{v-V}{v_0-0} \end{equation} |
| 反発係数を 相対速度としてとらえる | 衝突直後の相対速度=\(0\)つまり、おもりと物体は一体化 | 衝突直前と直後の相対速度は
大きさが同じで向きは逆 |
|
| 衝突直前直後の
力学的エネルギーの保存 |
保存されない | 保存されない | 保存される |
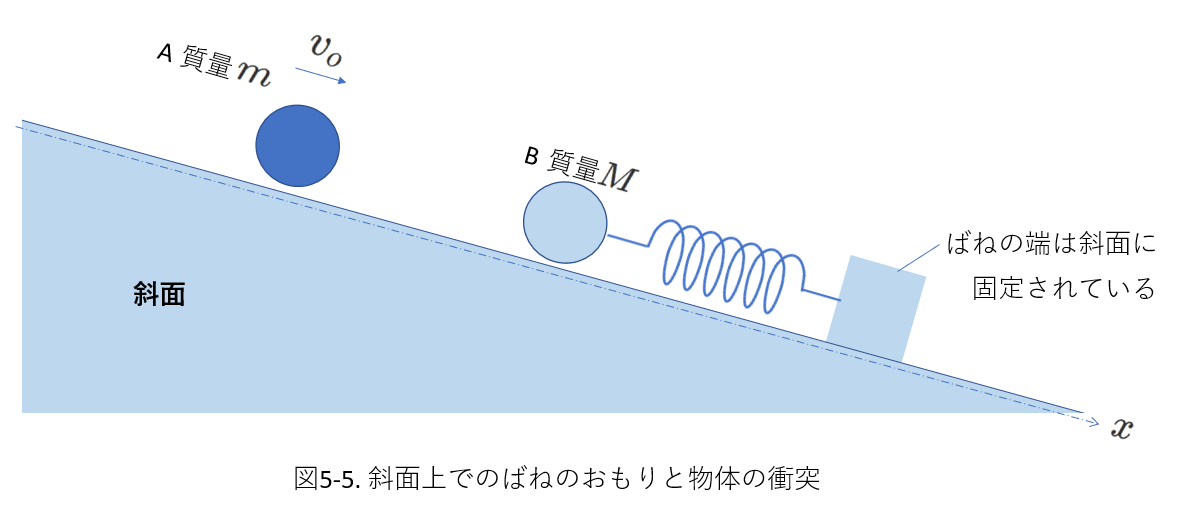
| その他の注意点 | 衝突直後から以後もおもりと物体が一体化されたままだとすると、単振動の”おもり(AとB)”の質量は\(m\)ではなく、\(m+M\)となります。
これにより、角振動数や下図5-5の場合の単振動の振動中心を求めるには、\(m+M\)を用います。 |
注1) 非弾性衝突は完全非弾性衝突(\(e=0\))を含みます。完全非弾性衝突は非弾性衝突の特別な場合です。
注2) 衝突は「弾性衝突」、あるいは、「完全非弾性衝突」であると、言葉で説明されることがほとんどですから、
これらの言葉の意味を覚えましょう。
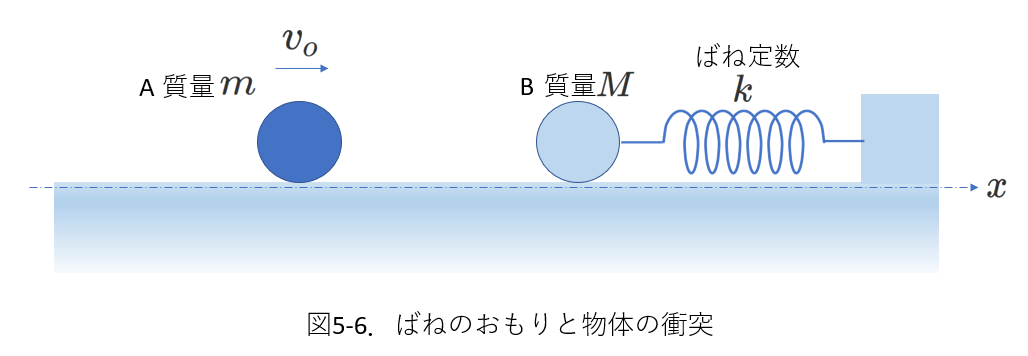
【例題】
右図5-6で、おもりBは静止しています。
そこに、質量\(m\) の物体Aが速度\(v_0\)で衝突しました。
運動はすべて直線上で起こるとします。
衝突が弾性衝突であるとして、衝突後に物体Aが床から見て左側に動く条件を求めましょう。
衝突では、運動量保存の式とはね返り係数(反発係数)の式を考えます。
弾性衝突ですから、はね返り係数\(e=1\)です。
衝突直後の、床から見たAとBの速度を\(v\)、\(V\)として、それぞれ次のようになります。
\begin{eqnarray} mv_0&=&mv +MV \tag{5-14} \\
1&=&-\frac{v-V}{v_0-0} \tag{5-15}
\end{eqnarray}
衝突後に、Aが左に動くということは、
\begin{equation} v \lt 0 \tag{5-16} \end{equation}
ということですから、(5-14)(5-15)式から\(v\)を求め、(5-16)式の条件に代入します。
(5-15))式から
\begin{eqnarray} V&=&v+v_0 \\
(5-14)式に代入して、 \\
mv_0&=&mv+M(v+v_0) \\
v&=&\frac{m-M}{m+M}v_0 \\
(5-16)式に代入して、 \\
\frac{m-M}{m+M}v_0 \lt 0 \\
したがって、&&m \lt M
\end{eqnarray}
となります。
次に、同じ図5-6において、衝突後AとBが一体化したとして、衝突後の単振動の振幅を求めます。
この一体化後の水平ばね振り子の単振動でわかっていることは、
・一体化によっておもりの質量は\(m+M\)に変わります。
・振動の中心はつりあいの位置(つまり、ばねが自然長のときのおもりの位置)は一体化前後で変わらず、
衝突した点が振動の中心です。
・衝突後のおもりの速度がわかれば、力学的エネルギー保存の式から振幅が求められそうです。
それでは、衝突直後のおもりの速度\(V_0\)を求めます。
一体化したということは、AもBも速度が\(V\)ということですから、
運動量保存の式は、
\begin{eqnarray} mv_0&=&mV_0+MV_0=(m+M)V_0 \tag{5-17} \\
V_0=\frac{mv_0}{m+M} \tag{5-18}
\end{eqnarray}
振幅をAとすると、振動の端で運動エネルギーは\(0\)ですから、力学的エネルギー保存の式は、
[衝突時のAとBの運動エネルギー]=[振動の端での弾性エネルギー]と表されます。
\begin{eqnarray} \frac{1}{2}(m+M)V_0^2&=&\frac{1}{2}kA^2 \tag{5-19} \\
A&=&\sqrt{\frac{m+M}{k}}V_0 \tag{5-20} \\
(5-18)式を代入して、A&=&\sqrt{\frac{m+M}{k}}\frac{mv_0}{m+M}=\frac{mv_0}{\sqrt{k(m+M)}}
\end{eqnarray}
となります。
【参考】
力学的エネルギー保存則を使わず、振動の中心での速度が\(A\omega\)で表されることを利用して、振幅\(A\)を求めることができます。
実際、上の例では、振動の中心で、(5-18)式で与えられる速さを持ちます。
また、この単振動の角振動数\(\omega\)は、おもりの質量が\(m+M\)で、ばね定数が\(k\)ですから、
\begin{equation} \omega=\sqrt{\frac{k}{m+M}} \end{equation}
これより、
\begin{eqnarray} A\omega&=&V_0 \\
A&=&\frac{V_0}{\omega}=\frac{mv_0}{m+M}\sqrt{\frac{m+M}{k}}=\frac{mv_0}{\sqrt{k(m+M)}}
\end{eqnarray}
同じ結果になりました。
Ⅵ.ばねについて
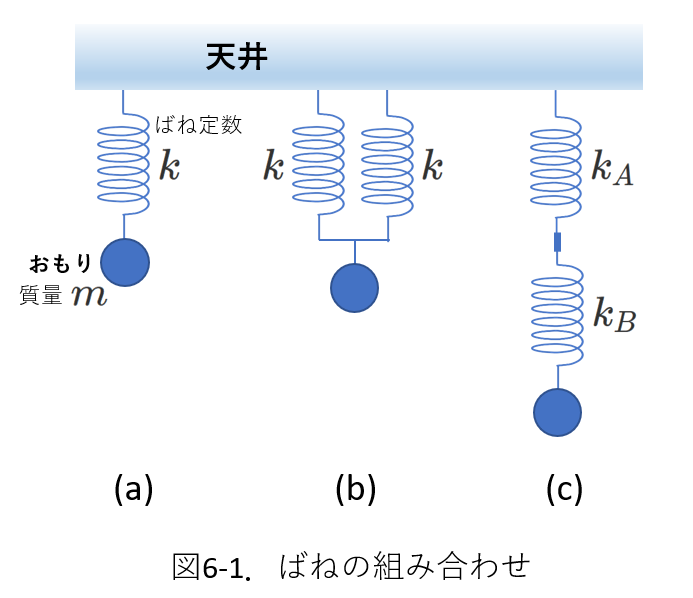
1.ばねを組み合わせる
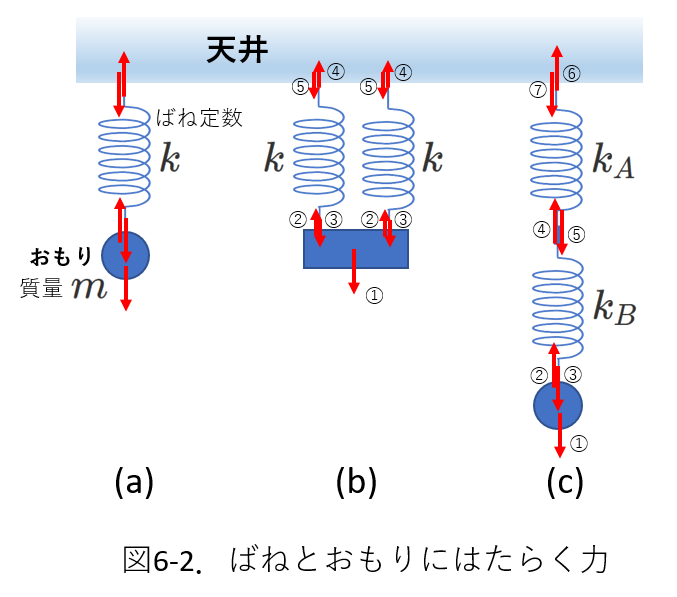
右図6-1の(b)と(c)では、2本のばねがおもりを支えています。
(b)では、ばね2本が並列に並んでいて、両方のばねが直接おもりに接続されています。
一方(c)では、2本のばねは直列に並んでいて、1本のばねだけがおもりに直接接続されています。
(b)、(c)のように2本のばねを組み合わせたときの全体としてのばね定数を求めます。
言い換えれば、2本の組み合わせばねと特性の等しい1本のばねのばね定数を求めることになります。
ここで、ばねの特性が等しいとは、ばねに同じ力を加えたときのばねの伸縮量が等しいということです。
ばねの弾性力の大きさ\(F\)は、ばねの伸びを\(x\)、ばね定数を\(k\)として\(F=kx\)と表されます。
この式から、伸び(\(x\))が同じならば\(k\)が大きいほど、力が大きくなります。
また、同じ力を加えたときには、ばね定数(\(k\))が大きいほど伸び(\(x\))は小さくなります。
ばね定数が大きいと、ばねは固く感じるということがわかります。
(b)の場合、同じ力で2本のばねを伸ばすわけですから、固く感じます。つまり、2本のばねを合成したばね定数は大きくなると言えます。
一方(c)の場合、2本のばねの伸びが加算されるので、ばね定数は小さくなると考えられます。
ばね定数をもとめるために、おもりとばねにはたらく力を図示します。図6-2のようになります。
(b)について、
図6-2では、おもりの形を変えて示しました。
おもりにはたらく力は、重力の①とふたつのばねによる弾性力の②です。そして、おもりは静止しているので、これらの力はつりあっています。
今、重力の①の大きさを\(F\)とすると、上のことから②の大きさ\(\frac{F}{2}\)です。
おもりとばねは接しているので、相互に力を及ぼしあいます。
おもりはばねから②の力を受け、ばねはおもりから③の力を受けます。そして、ふたつの力は向きが逆向きですが、大きさは同じです。
ばねと天井も力を及ぼしあっています。それが、④と⑤の力です。
以上のように、②~⑤の力の大きさは等しく、\(\frac{F}{2}\)です。
(b)の組み合わせばねに力\(F\)を加えると、
ふたつのばねのそれぞれに\(\frac{F}{2}\)の大きさの力が加わり、ふたつのばねのばね定数はどちらも\(k\)ですから、
ふたつのばねはそれぞれ、\(\frac{F}{2k}\)の伸びを示します。したがって、(b)のばねの伸びも\(\frac{F}{2k}\)です。
\(F\)の力を加えて伸びは\(\frac{F}{2k}\)ですから、合成したばね定数\(K\)は、
\begin{equation} K=\frac{ F }{\frac{F}{2k}}=2k \tag{6-1} \end{equation}
となります。
ばね定数が大きくなる(ばねが固くなる)という前述の予想が正しかったことがわかります。
(c)について、
(c)のおもりにはたらく力は、①の重力(\(F\))と、②のばねの弾性力です。
おもりは静止しているので、力はつりあっていて、②の大きさは\(F\)であることがわかります。
おもりと下側のばねは接しているので力を及ぼし合っています。
これが②と③で、ふたつの力は向きが逆向きですが、大きさは同じです。
下側のばねも静止しているわけですから、上側のばねから上向きに\(F\)の大きさの力④を受けているはずです。
同時に上側のばねは、下側のばねから下向きに\(F\)の大きさの力を受けています。
さらに上側のばねも静止しているわけですから、天井から上向きの\(F\)の力⑥を受けているはずです。
同時に天井は、上側のばねから下向きに\(F\)の大きさの力を受けています。
このように考えていくと、①~⑦の力の大きさはいずれも等しく、\(F\)です。
また、ひとつのばね(例えば下側のばね)に着目しますと、ばねは両端を上下に\(F\)の大きさの力で引っ張られていて伸びた状態です。
したがって、ばねの弾性力は縮む方向にはたらき、これがばねの両端の物体(おもりと上側のばね)を\(F\)の大きさで引っ張ることになります。
ここで大切なことは、
上側のばねの弾性力がおもりに直接はたらくことはないことです。
接しているところでの力の及ぼし合いを基本に考察しましょう。
下側のばね定数を\(k_B\)とすれば、\(F\)の力を受けたときの伸びは、\(\frac{F}{k_B}\),
上側のばね定数を\(k_A\)とすれば、\(F\)の力を受けたときの伸びは、\(\frac{F}{k_A}\)、
したがって、(c)の全体の伸びは、\(\frac{F}{k_A}+\frac{F}{k_B}\)ですから、合成したばね定数\(K\)は、
\begin{equation} K=\frac{F}{\frac{F}{k_A}+\frac{F}{k_B}}=\frac{k_Ak_B}{k_A+k_B} \tag{6-2} \end{equation}
となります。
念のため、検証しておきます。
\begin{eqnarray} \frac{k_Ak_B}{k_A+k_B}-k_A=\frac{k_Ak_B-k_A^2-k_Ak_B}{k_A+k_B}=\frac{-k_A^2}{k_A+k_B}\lt 0 \\
\frac{k_Ak_B}{k_A+k_B}-k_B=\frac{k_Ak_B-k_Ak_B-k_B^2}{k_A+k_B}=\frac{-k_B^2}{k_A+k_B}\lt 0
\end{eqnarray}
つまり、合成したばね定数\(K\)は\(k_A、k_B\)いずれよりも小さくなっています。
これも予想通りです。
また、下側のばねがとても固くて剛体とみなせる場合、つまり、\(k_B \to \infty\)のとき、
\begin{eqnarray} \frac{k_Ak_B}{k_A+k_B}=\frac{k_A}{\frac{k_A}{k_B}+1} \\
k_B \to \infty のとき、\\
\frac{k_Ak_B}{k_A+k_B} \to k_A
\end{eqnarray}
つまり、上側のばねだけがばねとしてはたらくことを示していて、合理的な結果になっています。
では、図6-2の(b)の場合に、おもりが運動(単振動)しているとして、運動方程式を立ててみましょう。
右図6-3で、鉛直上向きを\(x\)軸の正の向きとしています。
おもりが原点\(O\)にあるときばねが自然長の状態であるとして、おもりが\(x\)の位置にある場合を図6-3に図示しています。
したがって、\(x\gt 0\)でばねは縮んでいることになり\(x\)はばねの縮み量を表すことになります。
重力\(mg\)もばねの弾性力も図の状態でが下向きにはたらくことになります。
おもりの加速度を\(a\)として、加速度の正の向きを\(+x\)向きとして、運動方程式を立てると、
\begin{equation} ma=-2kx-mg=-2k\{x-\left(-\frac{mg}{2k}\right)\} \tag{6-3} \end{equation}
となります。
この運動方程式からも、ふたつのばねを合成したばね定数が\(2k\)であることがわかります。これは(6-1)式と一致しています。
(6-3)式からは振動の中心が\(-\frac{mg}{2k}\)であるこもわかります。
また、角振動数\(\omega\)と周期\(T\)は次にようになります。
\begin{eqnarray} \omega&=&\sqrt{\frac{2k}{m}} \\
T&=&\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{2k}}
\end{eqnarray}
次に図6-4の場合の運動方程式を立ててみます。
おもりの両側にふたつのばねが接続されています。左側のばねのばね定数は\(k_A\)、右側は\(k_B\)で、それぞれのばねの他端は枠に固定されてます。
おもりと枠の間には摩擦はないものとします。
今、図6-4の状態でふたつのばねは自然長であるとします。
この状態から、おもりを右に\(L\)だけ動かして静かに放しました。
このときの単振動の周期\(T\)を求めます。
単振動の運動方程式を立てて、角振動数を求め、そこから周期を計算します。
おもりが\(x(\gt 0)\)の位置にあるときにおもりにはたらく力を図6-5に示しました。
運動する方向に合わせて\(x\)軸を左右方向に設定します。
また、変位がそのままばねの伸縮量になると式が立てやすいことから、それぞれのばねが自然長になっている図6-4の状態のおもりの位置を\(x\)軸の原点とします。
このときのおもりの加速度を\(a\)として、加速度の正の向きを\(+x\)向きとすると、運動方程式は、
\begin{equation} ma=-k_Ax-k_Bx=-(k_A+k_B)x \tag{6-4} \end{equation}
です。
これより、各振動数\(\omega\)と周期\(T\)は、
\begin{eqnarray} \omega&=&\sqrt{\frac{k_A+k_B}{m}} \tag{6-5} \\
T&=&\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k_A+k_B}}
\end{eqnarray}
2.振幅を変えても周期は変わらない
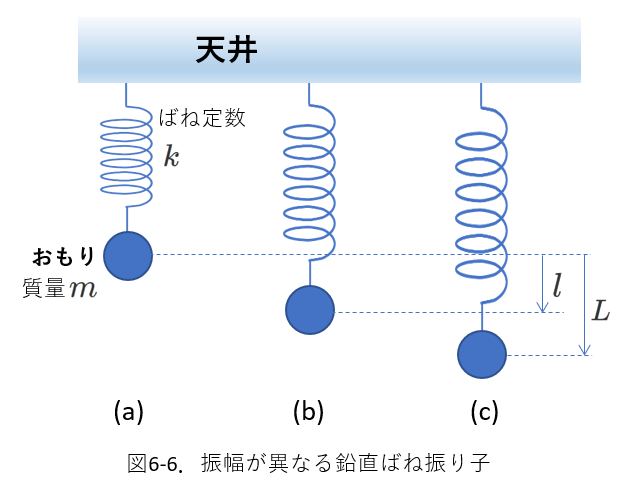
図6-6に鉛直ばね振り子を示します。
(a)は静止状態で、重力とばねの弾性力がつりあっている状態です。
単振動したときには、この点が振動の中心となります。
この状態から、(b)のように\(l\)の距離だけ引き伸ばして、静かに手を放すと、単振動をしました。
(c)では、さらに長くばねを\(L\)の距離引き伸ばして、静かに手を放して、単振動させました。
(b)と(c)の振動を比べると、角振動数は同じで、振幅だけが異なります。ばね振り子では、角振動数はおもりの質量とばね定数だけで決まります。
振幅が異なっていて角振動数が同じなのは、おもりの速度が異なるためです。
(b)(c)の振幅はそれぞれ\(l、L\)です。
したがって、単振動の角振動数を\(\omega\)とすると、(b)(c)の単振動の最大の速さ(振動の中心での速さ)は、それぞれ\(l\omega\)、\(L\omega\)です。
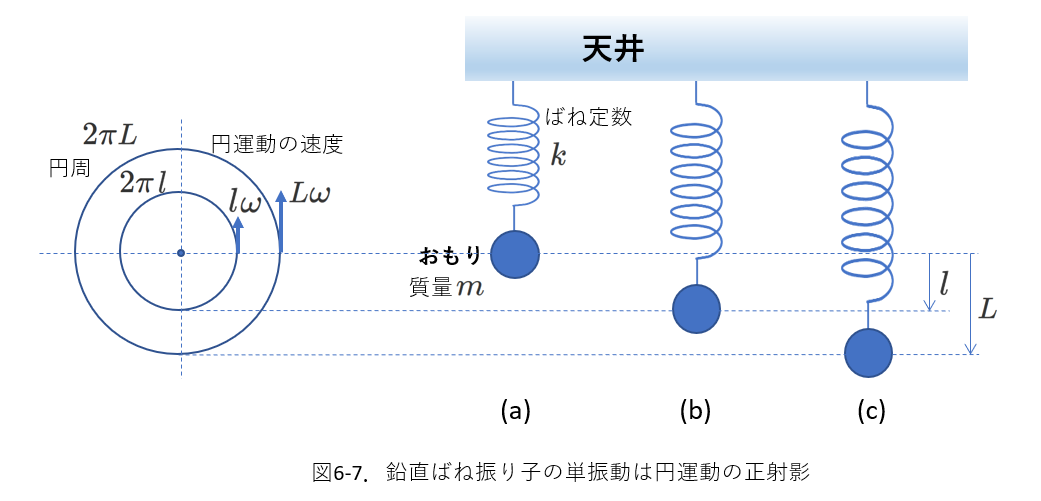
振幅が異なっても角振動数が同じというのは、図6-7の「単振動は円運動の正射影」を考えるとわかりやすいです。
図6-7の左側にその円運動が示されています。
この円運動は等速度です。
(b)は、円周\(2\pi l\)を速さ\(l\omega\)で一周すると、\(\frac{2\pi l}{l\omega}=\frac{2\pi}{\omega}\)の時間(1周期)がかかります。
(c)は、円周\(2\pi L\)を速さ\(L\omega\)で一周すると、\(\frac{2\pi L}{L\omega}=\frac{2\pi}{\omega}\)の時間(1周期)がかかります。
振幅が\(n\)倍されると、単振動のもとの円運動の半径が(したがって、円周が)\(n\)倍となりますが、円運動の速さも\(n\)倍になるため周期は変化しないということが理解できます。
Ⅶ.ばね以外の単振動
1.液体に浮かんだ浮きの単振動
ここに書かれていた例題について、内容を精査します。
その間、しばらく非表示にさせていただきます。
Ⅷ.振幅、速さの求め方、振動中心の求め方をまとめる
1.振動範囲
運動エネルギー\(\geqq 0\)
あるいは、速さ\(v=0\)として、力学的エネルギー保存から振動端を求める。
2.振動の中心
①運動方程式を立式して
\(ma=-k(x-x_0)\)の式の形にして、\(x_0\)が振動の中心
運動方程式において、加速度=\(0\)
②力のつりあいから
運動方程式の加速度(または、力)=\(0\)
力がつりあっている
③「1.振動範囲」で上端下端を求めたら、その中央が振動の中心
3.振幅
①「1.振動範囲」で上端下端を求めたら、(上端-下端)×\(\frac{1}{2}\)
②運動の意味から、
引っ張って離せばそこが上端、あるいは下端(速さが0だから)、それと振動の中心との差を考える。
Ⅸ.単振動に近似する
1.近似式
一般的に\(x\)の関数は、マクローリン展開を使って、\(x\)の多項式で表すことができます。
次に、マクローリン展開の例を掲げます。
\begin{eqnarray} (1+x)^n&=&1+nx+\frac{n(n-1)}{2}x^2+\frac{n(n-1)(n-2)}{6}x^3+\frac{n(n-1)(n-2)(n-3)}{24}x^4+・・・ \tag{9-1} \\
\sin x&=&x-\frac{1}{6}x^3+\frac{1}{120}x^5-・・・ \tag{9-2} \\
\cos x&=& 1-\frac{1}{2}x^2+\frac{1}{24}x^4-・・・ \tag{9-3} \\
\tan x&=&x+\frac{1}{3}x^3+\frac{2}{15}x^5+・・・ \tag{9-4}
\end{eqnarray}
上の式を近似に使うことを考えます。
仮に、\(x \ll 1\)のとき、
\begin{equation} x \gt x^2 \gt x^3 \gt x^4 \gt x^5 ・・・ \end{equation}
つまり、\(x \ll 1\)のとき、\(x\)の次数が高いほど、その値は小さくなります。
したがって、必要な精度に応じて、ある次数以上を省略することで近似式が得られます。
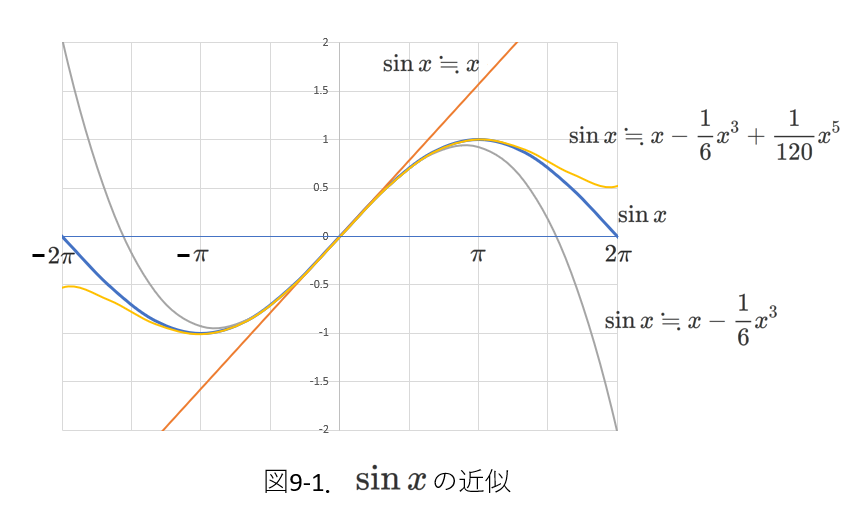
例えば、(9-1)~(9-4)式において、\(x^3\)以上の項を省略して、次の近似式が得られます。
\begin{eqnarray} x \ll 1 のとき、 \\
(1+x)^n& \fallingdotseq&1+nx+\frac{n(n-1)}{2}x^2 \tag{9-1'} \\
\sin x& \fallingdotseq&x \tag{9-2'} \\
\cos x& \fallingdotseq& 1-\frac{1}{2}x^2 \tag{9-3'} \\
\tan x& \fallingdotseq&x \tag{9-4'}
\end{eqnarray}
高い次数の項まで含めれば、近似できる\(x\)の範囲は拡がります。
\(\sin x\)について、次の図9-1にこれを示します。
1)ほとんどの場合、近似式は問題文中で与えられます。
その場合には、これ以外の自分で覚えている近似式を使うことは控えましょう。
基本的には、立てた式をその近似式を使える形に変形して、近似式を適用します。
2)複数の関数の近似式を持ちいる場合、省略する項の次数を揃えます。
ある関数は\(x^2\)以上を省略、別の関数は\(x^3\)以上を省略するということはしません。
3)例えば、単振動を表す運動方程式の復元力の式は\(x\)の1次関数です。
したがって、立式した運動方程式を単振動を表す式に近似しようとする場合、
これに用いる近似式は\(x\)の1次の項を含むべきで、\(x^2\)以上の項を省略することになります。
前述したように、ほとんどの問題では近似式が与えられるので、上記のことを考える必要なく、与えられた式を用います。
マクローリン展開については、ここでは述べませんが、
\(x=0\)の近傍で、関数はマクロ―リン展開により次のように展開できます。
\begin{equation} f(x)=f(0)+\frac{1}{1!}f^{(1)}(0)x+\frac{1}{2!}f^{(2)}(0)x^2+\frac{1}{3!}f^{(3)}(0)x^3+・・・ \tag{9-5} \end{equation}
2.単振り子
教科書に出ている単振り子を例にとって近似式について考えてみます。
図9-2を参照してください。
天井から垂らした長さ\(l\)の糸に質量\(m\)のおもりがつながっています。
糸がぴんと張った状態で糸を傾けながらおもりを持ち上げ、静かに手を放せば振り子の運動をします。
振れが大きいときには、鉛直面内の円運動と考えられて、その場合には、力学的エネルギー保存の式と円運動の運動方程式を使って問題を解くことになります。
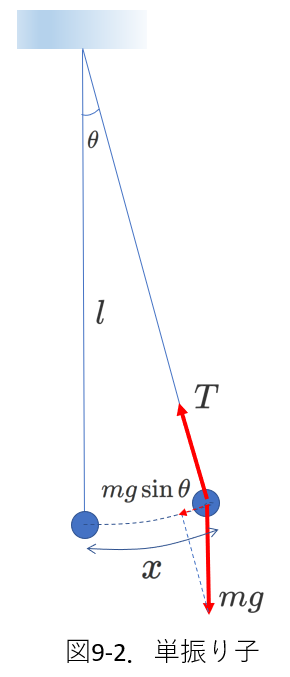
さて、振れが小さい(\(\theta \approx 0\))ときに、この振り子の運動が単振動に見なせることを示します。
図9-2で、おもりが鉛直最下端にある点を原点\(O\)として、\(O\)から円弧に沿った変位を\(x\)と表します。
\(x\)について、運動方程式を立てるので、力は円弧に沿った方向(実際には、\(x\)の点での接線方向)の成分を考えます。
図9-2に示すように、重力のこの方向の成分は、\(mg\sin \theta\)となりますから、運動方程式は、
\begin{equation} ma=-mg\sin \theta \tag{9-6} \end{equation}
です。
ここで、\(x=l\theta\)と表すことができることから、
\begin{equation} ma=-mg\sin\frac{x}{l} \tag{9-7} \end{equation}
振れ角\(\theta\)が十分小さいということは、糸の長さ\(l\)に比べて変位\(x\)が十分に小さいということですから、\(\frac{x}{l} \ll 1\)が成立して、\(\sin\frac{x}{l} \fallingdotseq \frac{x}{l}\)の近似が成り立つため、
(9-7)式は次のように変形できます。
\begin{equation} ma=-\frac{mg}{l}x \tag{9-8} \end{equation}
この近似は、(9-2’)を用いています。
単振動を表す式に変形しようという場合、復元力は\(x\)の1次式で表されるため、\(x\)の1次の項を残すように近似します。
ここから、角振動数\(\omega\)と周期\(T\)は、
\begin{eqnarray} \omega&=&\sqrt{\frac{g}{l}} \tag{9-9} \\
T&=&\frac{2\pi}{\omega}=2\pi\sqrt{\frac{l}{g}} \tag{9-10}
\end{eqnarray}
関連ページ
- 作図
- 物理の問題を解く場合、図を描くことは必須と言えます。図を活用することで、考察が進み、その結果ミスを減らすことができます。図を活用する場合の注意点を説明しています。
- 運動方程式
- 物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。
- モーメントの考え方
- 力のモーメントについて、基本的注意事項のいくつかを説明しています。
- 運動量保存則を使う問題
- 運動量保存則は、力学でも最も重要な概念のひとつです。運動量が保存される場合と保存されない場合について説明し、例題を掲げました。
- 張力
- 糸につながれたおもりの運動では、糸の張力を考慮します。張力を考える場合のヒントを説明しています。
- 運動エネルギーと仕事の関係
- 運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。
- 力学的エネルギー保存則を考える
- 力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。
- 力積
- 力学は物理の基礎とも柱とも言えます。しっかり勉強して理解を深めましょう。
- 円運動
- 円運動を考えるには、向心力を用いて運動方程式を立てるか、遠心力で力のつりあいを考えます。円運動の問題は難しく感じますが、出題のパターンは多くありません。
- 二体問題 Ⅰ
- 互いに力を及ぼし合う二つの物体の動きを考えます。
.png)
.png)
.png)

.png)
.png)
.png)
.png)
.png)
.png)
が単振動する場合.png)
.png)
.png)