物理の大学入試問題をいかにして解くか

トップページ ＞ 力学 ＞ 円運動

 

１．運動方程式

 

　運動方程式は、
\begin{equation} ma=F \tag{1-1} \end{equation}
の形に表します。
　ここで、\(m\)は物体の質量、\(a\)は物体の加速度、\(F\)は物体にはたらく力です。

 

　力学の問題を解く場合、注目する物体にはたらく力を数えあげ、それをもとにして（1-1）式の形に運動方程式を立てます。
運動方程式を見れば、物体がどのような運動をするか知ることができます。
注）物体の運動を知るということは、物体の位置と速度の時間変化を知ることです。
　　加速度（の時間変化）と、初期位置と初速度がわかれば、任意の時刻の物体の位置と速度を求められます。

 

　例えば、
\begin{eqnarray} ma&=&"一定"　　\tag{1-2} \\
ma&=&-kx \tag{1-3}
\end{eqnarray}
　（4-2）式の運動方程式からは、加速度\(a\)が一定であり、等加速度運動をすることがわかります。
ただし、等加速度運動は力がはたらく向きに行われることに注意します。
（必ずしも物体が動く向きに等加速度運動をするわけではありません。）

 

　物体を投げ上げた場合や自由落下の場合、重力の向き（鉛直下向き）に等加速度運動をします。
それに垂直な方向（水平方向）に力がはたらいていなければ、物体はその方向に運動をしないか、または、等速度運動をします。
　したがって、2次元で見た場合、直線運動をする場合もあれば、放物運動をする場合もあります。

 

　(1-2）式は、
\begin{equation} m\frac{d^2x}{dt^2}="一定"　\tag{1-4} \end{equation}
と微分方程式に表すことができて、これは解くことができます。

 

　（1-4）式は高校で解くことのできる数少ない微分方程式のひとつで、これを解けば、位置\(x\)、速度\(v=\frac{dx}{dt}\)が求められます。

 

　ちなみに、物体の\(t=0\)での速度と座標をそれぞれ\(v_0\)、\(x_0\)として、
\begin{eqnarray} \frac{dx}{dt}=v&=&v_0+at \tag{1-5} \\
x&=&x_0+v_0t+\frac{1}{2}at^2 \tag{1-6}
\end{eqnarray}
と解けますが、その都度微分方程式を解くのはめんどうですから、(1-5)(1-6)式を公式として覚えすぐに活用できるようにしておきます。

 

 

　(1-3)式の運動方程式において、\(x\)は物体の座標であり、\(-k\lt 0\)であるとします。
このとき、（1-3）式の運動方程式は、\(-kx\)が復元力を表していて、物体は単振動をすることがわかります。

 

　このように、運動方程式を立てれば、物体がどのような運動をするかわかります。

 

 

 

　さて、円運動の運動方程式は、次のように表されます。
\begin{eqnarray} m\frac{v^2}{r}&=&F \tag{1-7} \\
または、mr\omega^2&=&F \tag{1-8}
\end{eqnarray}
　ここで、\(v、r、\omega\)は、それぞれ円運動の速さ、半径、角速度を表します。
また、\(F\)は物体にはたらく力の合力の円運動の中心に向いた成分を表し、中心に向かう向きが正となります。
\(F\)を「向心力」と呼びます。
　「向心力」は（重力、垂直抗力、摩擦力というような）力の一種類ではありません。円運動を維持するための円運動の中心に向いた力の呼び名です。
具体的には、張力や垂直抗力や重力など、あるいは、それらの合力の円運動の中心に向いた成分が「向心力」の役目を担います。

 

　次に、円運動の運動方程式を立てる目的について説明します。

 

 

 

２．円運動の運動方程式を立てる目的

 

　円運動の運動方程式を立てる目的は、
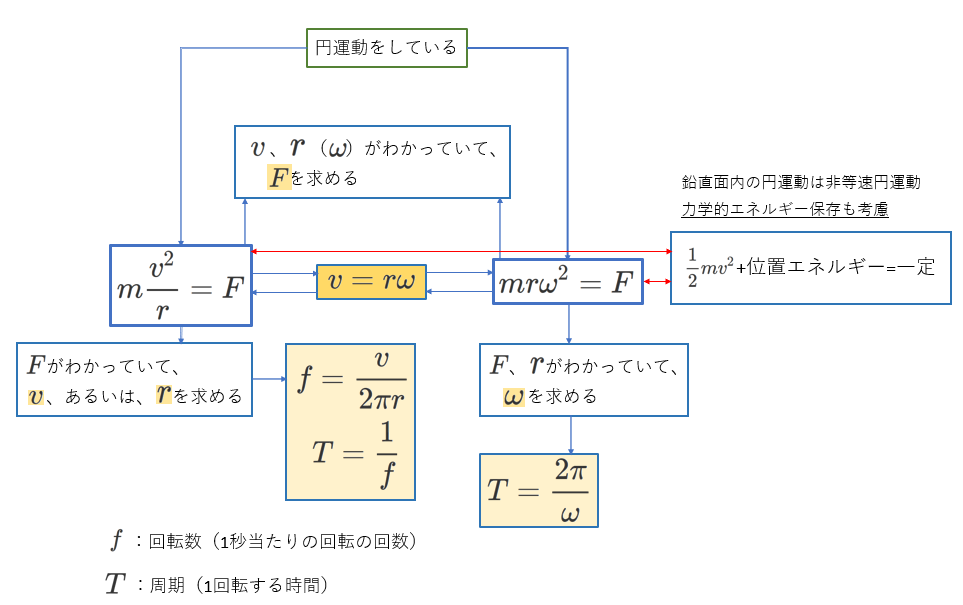
　①　（1-7）（1-8）式の\(v、r、\omega\)、すなわち、円運動の速さ、半径、角速度のうちのひとつを求める。
　　　特に、向心力の大きさがわかっている場合には、この目的で立式されます。

 

　②　向心力を構成する、張力や垂直抗力を求める。
　　　こちらは、\(v、r、\omega\)がわかっている場合になります。

 

　以下に具体的な例を挙げて、①と②について考えます。

 

 

　①円運動の半径または速さ（または角速度）を求める

 

　円運動の方程式はひとつですから、ひとつの未知数しか求めることはできません。
つまり、円運動の半径\(r\)、または、速さ\(v\)を求めるために立式します。
また、\(r\)と\(v\)がわかれば、\(\omega\)は次の関係式から求めることができます。
\begin{equation} v=r\omega \tag{1-9} \end{equation}

 

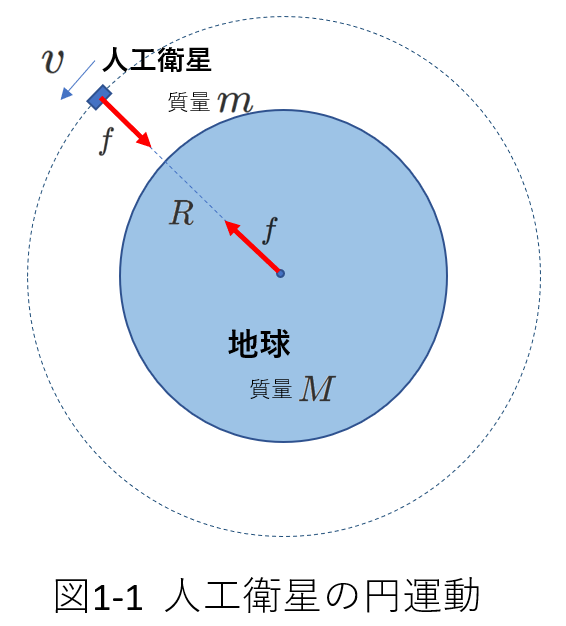
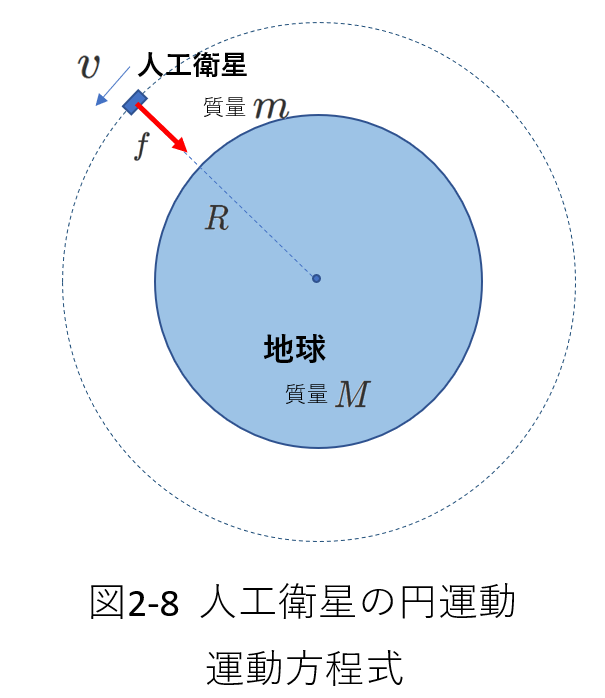
　例題として、地球の周りを円軌道で回っている人工衛星を考えます。

　右の図1-1に示すように、質量\(m\)の人工衛星が地球の周りを円軌道に沿って回っています。
人工衛星の速さを\(v\)、地球の重心からの距離を\(R\)とします。

 

　さて、地球と人工衛星の間には万有引力（図では\(f\)）がはたらきます。
人工衛星が受ける万有引力の向きは、円軌道のどの位置においても地球の重心に向かう向きです。
したがって、万有引力\(f\)が向心力となります。

 

　宇宙空間から人工衛星の運動を見ると、万有引力がなければ円軌道の接線の方向に飛び去ってしまうはずの人工衛星を、万有引力が引き止めているように見えます。

 

　万有引力定数を\(G\)で表せば、万有引力\(f\)は、
\begin{equation} f=G\frac{mM}{R^2} \tag{1-10} \end{equation}
となります。ここで、\(M\)は地球の質量です。

 

　したがって、この場合の円運動の運動方程式は、
\begin{eqnarray} m\frac{v^2}{R}&=&G\frac{mM}{R^2} \tag{1-11} \\
または、mR\omega^2&=&G\frac{mM}{R^2} \tag{1-12}
\end{eqnarray}
　この例では、向心力の大きさがわかっている（向心力の式に\(R\)が含まれていますが）ので、（1-11）(1-12)式から\(R\)、\(v\)（または、\(\omega\)）のうちの一つを求られます。
（1-11）式について言えば、\(R\)が与えられていて\(v\)を求める。または、\(v\)が与えられて\(R\)を求めます。
　式に表せば、
\begin{eqnarray} v&=&\sqrt{\frac{GM}{R}} \tag{1-13} \\
R&=&\frac{GM}{v^2} \tag{1-14}
\end{eqnarray}

 

 

 

　②向心力を構成する、張力や垂直抗力を求める

 

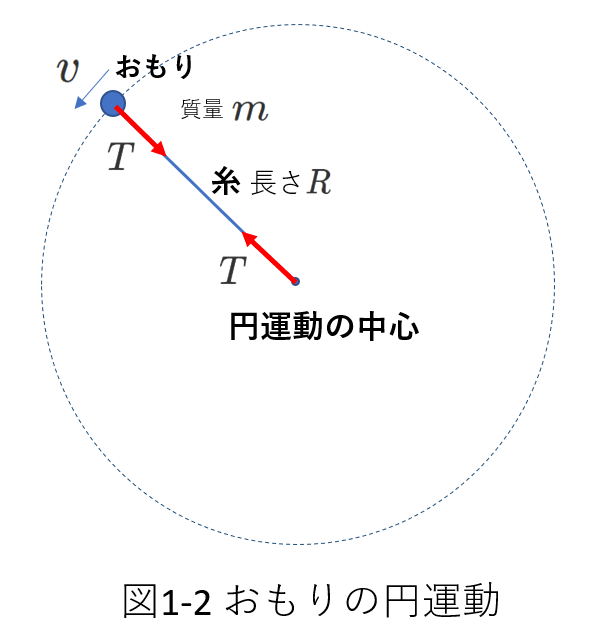
　右の図1-2では、一方の端を固定された糸の他端に質量\(m\)のおもりが繋がっていて、水平面内で糸がぴんと張った状態で円運動をしています。

 

　おもりにはたらく力は糸の張力\(T\)と重力です。
このうち重力は、「水平面内で円運動をしている」ことから、円運動の中心に向く成分を持っていません。
　したがって、向心力は糸の張力\(T\)です。

 

　円運動の運動方程式は次のようにあらわされます。
\begin{eqnarray} m\frac{v^2}{R}&=&T \tag{1-15} \\
または、mr\omega^2&=&T \tag{1-16}
\end{eqnarray}
　問題文中で\(R\)や\(v\)は既知とされていれば、（1-15）（1-16）式は糸の張力\(T\)を求めるために使われます。

 

 

 

 

　３．円運動の運動方程式を考える

 

　運動方程式は、[質量]×[加速度]=[力]の形で立式されますから、
（1-7）（1-8）の円運動の運動方程式は、半径\(r\)、速さ\(v\)で円運動していると観察された物体には、\(m\frac{v^2}{r}\)の加速度がはたらいていると考えていることになります。
　また、半径\(r\)、角速度\(\omega\)で円運動していると観察された物体には、\(mr\omega^2\)の加速度がはたらいていると考えていることになります。

 

　そこで、ここでは、円運動の加速度を求めてみます。
　

 

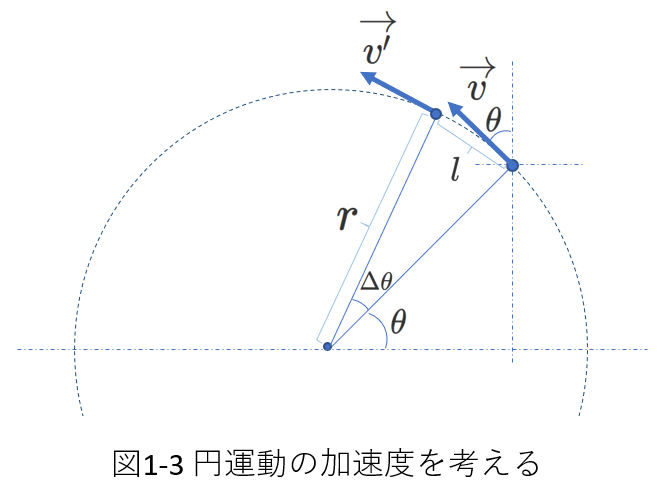
　右の図1-3で、小物体が半径\(r\)、速さ\(v\)で左回りに円運動をしているものとします。
今、小物体と円運動の中心を結ぶ線が基準線（図では横線）となす角度が\(\theta\)のときの小物体の速度ベクトルを\(\overrightarrow{v}\)、それから\(\Delta t\)の時間の間に角度が\(\Delta \theta\)増したときの速度ベクトルを\(\overrightarrow{v'}\)とします。
　\(\Delta t\)の間に小物体が進む円弧の長さを\(l\)とすれば、次の式が成り立ちます。
\begin{eqnarray} l=v\Delta t=r\Delta \theta \\
これより、　\Delta t=\frac{r}{v}\Delta \theta \tag{1-17}
\end{eqnarray}

 

　また、上記の条件から、\(|\overrightarrow{v}|=|\overrightarrow{v'}|=v\)ですから、\(\overrightarrow{v}\)と\(\overrightarrow{v'}\)を成分表示すれば、
\begin{eqnarray} \overrightarrow{v}&=&(-v\sin\theta、v\cos\theta) \tag{1-18} \\
\overrightarrow{v'}&=&\left(-v\sin(\theta+\Delta\theta)、v\cos(\theta+\Delta\theta)\right) \tag{1-19}
\end{eqnarray}

 

　求める加速度を\(\overrightarrow{\alpha}=(\alpha_x、\alpha_y)\)として、
\begin{eqnarray} \overrightarrow{\alpha}&=&\frac{\overrightarrow{v'}-\overrightarrow{v}}{\Delta t} \\
&=&\frac{v}{r}\frac{\overrightarrow{v'}-\overrightarrow{v}}{\Delta\theta} \tag{1-20}
\end{eqnarray}

 

　（1-20）式に（1-18）（1-19）を適用して、\(\alpha_x\)を取り出すと、
\begin{eqnarray} \alpha_x&=&\frac{v}{r}\frac{-v\sin(\theta+\Delta\theta)-(-v\sin\theta)}{\Delta\theta} \\
&=&-\frac{v^2}{r}\frac{\sin(\theta+\Delta\theta)-\sin\theta}{\Delta\theta}
\end{eqnarray}
　\(\alpha_x\)を求めるために、上式の\(\Delta\theta\to 0\)の極限を考えます。
\begin{eqnarray} \alpha_x&=&\lim_{\Delta\theta \to 0} \{-\frac{v^2}{r}\frac{\sin(\theta+\Delta\theta)-\sin\theta}{\Delta\theta}\} \\
&=&-\frac{v^2}{r}\frac{d}{d\theta}\sin\theta \\
&=&-\frac{v^2}{r}\cos\theta \tag{1-21}
\end{eqnarray}
　上式で最初の式の右辺が微分の定義式になっていることに注意してください。
　同様にして、
\begin{equation} \alpha_y=-\frac{v^2}{r}\sin\theta \tag{1-22} \end{equation}

 

　したがって、加速度の大きさは、
\begin{equation} \sqrt{\alpha_x^2+\alpha_y^2}=\frac{v^2}{r} \end{equation}
となります。

 

　また、
\begin{equation} (\alpha_x、\alpha_y)=\frac{v^2}{r}(-\cos\theta、-\sin\theta)　\end{equation}
のベクトルの向きは円運動の中心に向かう向きであることがわかります。
　これで、円運動の加速度は円運動の中心の向きで大きさが\(\frac{v^2}{r}\)であることが証明できました。

 

　また、弧度法の定義\(\theta=\frac{l}{r}\)から\(l=r\theta\)であることが導かれます。
\(l=r\theta\)の両辺を時間で微分すると、
\begin{eqnarray} \frac{dl}{dt}&=&v=r\frac{d\theta}{dt}=r\omega \\
つまり、v&=&r\omega \tag{1-23} \\
これから、m\frac{v^2}{r}&=&mr\omega^2
\end{eqnarray}

 

 

 

 

４．まとめ

 

　以下に、円運動に関する式をまとめます。
ここで、\(f\)は円運動の回転数で、１秒当たりの回転の回数を表します。
また、\(T\)は円運動の周期で、１回転に要する時間を表します。

 

 

 

　前章では、円運動を運動方程式で記述しました。
円運動を記述するのには、遠心力を使う方法もあります。
ふたつの違いは、どこから観察するかの立場の違いによります。
「Ⅰ．円運動：運動方程式」の図1-1を例にして、考えます。

 

 

１．観測する立場の違いについて

 

　遠心力に入る前に、観察する場所が変わると運動の見え方がどのように変わるかをまとめます。
これは、同時に「慣性力」を導入する必要性の説明となります。

 

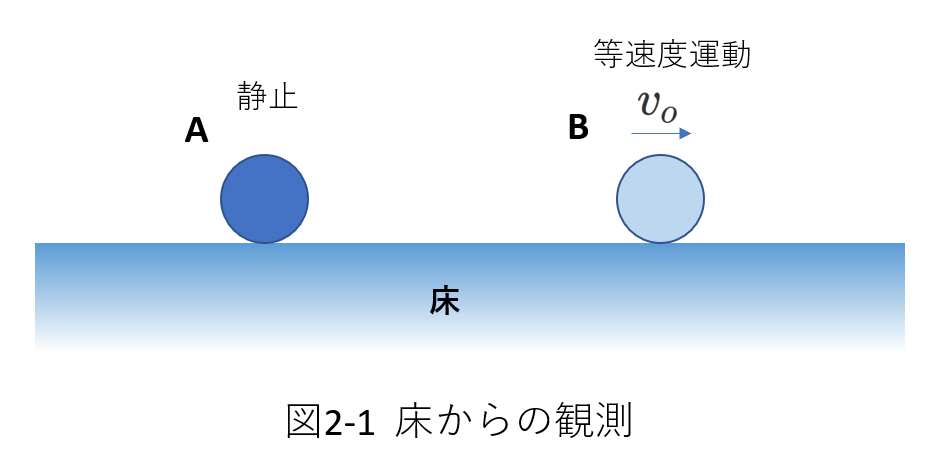
　図2-1を見てください。

　床の上に物体AとBがあり、どちらにも力ははたらいていません。
　A、Bの質量はどちらも\(m\)とします。
この状態で床に対して（言い換えれば、床に立って観測すると）Aは静止していて、Bは右向きに速さ\(v_0\)で等速度運動をしています。
　つまり、慣性の法則が成り立っています。

 

　観測者は運動を記述するための座標系を自分で設定して観測するわけですが、このとき慣性の法則（運動の第一法則）や\(F=ma\)（運動の第二法則）が成り立つ場合、その座標系を慣性系といいます。この言葉「慣性系」は高校の物理には出てこないので覚える必要はありません。

 

 

 

 

　次に、観測者がBと一緒に運動する場合、その観測者はAがどのような運動をしていると認識するかを考えます。

 

　これは図2-2のようになります。

注） 描くのが難しいため、Bから観測と言いながら、床から観測したような図になっている点はご容赦ください。

 

　さて、BからAを見れば、Aは左向きに速さ\(v_0\)で等速度運動をしているように見えます。
これは、Bに対するAの相対速度を観測したことになります。

 

　この場合、Aについて、「力がはたらいていなければ、静止、あるいは、等速度運動をする」という慣性の法則が成り立ちますから、この場合も床から観測したときと同じく慣性系で観測したことになります。

 

 

 

 

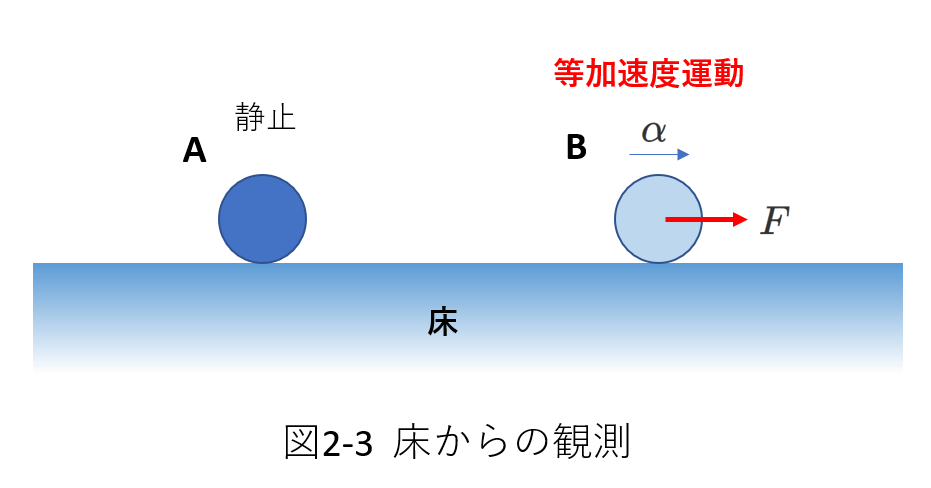
　では、図2-3の場合はどうでしょう。

　図2-3では、床の上に物体A,Bがあり、Aは床に対して静止しており、Bは一定の力\(F\)を受けて加速度の大きさ\(\alpha\)で右向きの等加速度運動をしています。

 

　床にいる観測者が見れば、Aには力がはたらいていないので静止し続けていて、Bには力\(F\)がはたらいているので\(m\alpha=F\)で決まる等加速度運動をしていると、理解できます。

 

 

 

 

 

　次に、Bと一緒に運動する観測者からAの運動を観察します。

 

　図2-4のように、Ｂにいる観測者は、Ｂが大きさ\(\alpha\)で左向きの等加速度運動をしていると観測します。
　これは、Bに対するAの相対加速度を考えたことになります。

 

　しかし、Aにはたらく力は存在しません。
力がはたらいていないのに、加速度運動をしていることになりますから、運動の第二法則が成立しません。
この場合、座標系は非慣性系であるということになります。

 

 

　さて、非慣性系から観測した場合にも、運動の法則が成り立つようにするために考えられたのが、慣性力です。
これはつじつまを合わせるためのみかけの力で、重力や張力や抗力などの実際に存在する力とは異なります。

 

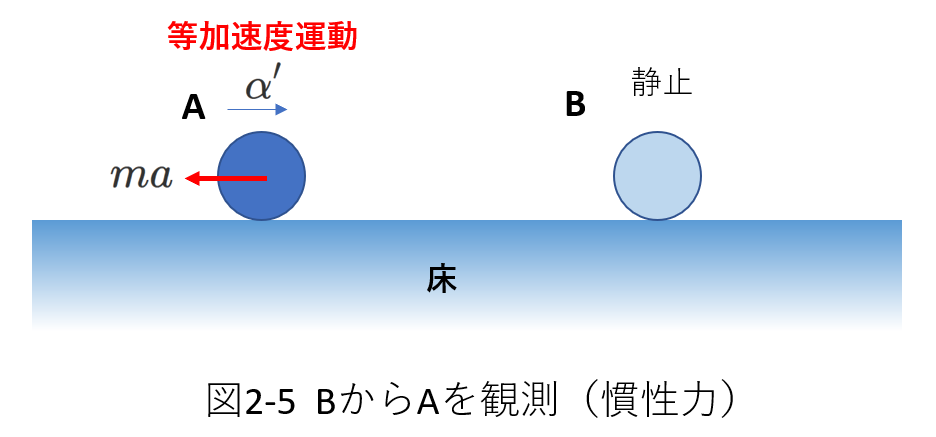
　慣性力を図2-5に示します。
Aにはたらく慣性力は、\([Aの質量]×[-Bの加速度]=-m\alpha\)で表されます。

 

　したがって、Aについて、その加速度を\(\alpha'\)として慣性力を考えた運動方程式を立てると、右向きを加速度と力の正の向きとして、
\begin{eqnarray} m\alpha'&=&-m\alpha \\
\alpha'&=&-\alpha
\end{eqnarray}
となり、図2-4の観測結果と一致します。
　非慣性系でも、慣性力を導入することにより、力がはたらくことにより加速度運動をするという運動の第二法則を見かけ上成立させることができるようになりました。

 

 

 

 

　もう少し、観察する立場の違いと慣性力について例をあげて考えます。

 

　図2-6を見てください。

　電車が等加速度運動をしています。加速度の向きは左向きで大きさは\(\alpha\)です。
質量\(m\)のおもりが電車の天井から糸で吊られています。
電車が等加速度運動をしている状態で、おもりは鉛直方向から角度\(\theta\)かたむいています。

 

　さて、電車の外から、線路に対して静止している観測者が、電車とおもりを観測します。
すると、電車とおもりはともに加速度\(\alpha\)の等加速度運動をしていることがわかります。

 

　電車は自身の動力から力を得て等加速度運動をしています。
おもりについて考えるために、おもりにはたらく力を図示すると、図2-6のようになります。

 

　おもりにはたらく力は、重力\(mg\)と糸からの張力\(T\)です。
つまり、\(T\)と\(mg\)の合力により、おもりは\(\alpha\)の大きさの加速度運動をしていると考えられます。
図から、この合力の大きさは\(T\)の水平成分の大きさに等しいことがわかります。
　また、鉛直方向には静止しているわけですから、この方向には力はつりあっていることになります。

 

　そこで、力と加速度の正の向きを左向きとして、
\begin{eqnarray} つり合いの式&：&T\cos\theta=mg \tag{2-1} \\
運動方程式&：&m\alpha=T\sin\theta \tag{2-2}
\end{eqnarray}
となります。
　これから、\(\alpha\)を\(\theta\)と\(g\)で表すことができます。
（2-1）式から、
\begin{equation} T=\frac{mg}{\cos\theta} \end{equation}
　これを（2-2）式に代入すれば、
\begin{equation} \alpha=\frac{T\sin\theta}{m}=\frac{mg\sin\theta}{m\cos\theta}=g\tan\theta \tag{2-3} \end{equation}

 

 

 

 

　次に、観測者が電車の車内にいて電車と一緒に運動している場合を考えます。
この場合、観測者には、おもりが鉛直方向から\(\theta\)の角度だけ傾いて静止しているように観測されます。

 

　おもりにはたらく力は重力\(mg\)と糸からの張力\(T\)だけで、これらの力はあきらかにつり合っていません。
したがって、加速度運動をするはずですが、実際には静止して見えます。
運動の法則が成立しませんから、観測している座標系は非慣性系だということになります。

 

　つじつまを合わせるため慣性力を導入します。

　これを、図2-7に示します。
おもりにはたらく慣性力は、\([おもりの質量]×[-電車の加速度]=-m\alpha\)で表されます。
慣性力の大きさは\(m\alpha\)、向きは右向きです。

 

　おもりが静止して見えることから、この重力と張力と慣性力の3つの力がつりあっている、あるいは、3つの力の合力が\(0\)となります。
　鉛直方向と水平方向の成分に分けて、それぞれのつり合いの式を立てると、
\begin{eqnarray} 鉛直方向&：&T\cos\theta=mg \tag{2-4} \\
水平方向&：&m\alpha=T\sin\theta \tag{2-5}
\end{eqnarray}
　（2-4）式は同じつり合いの式ですから、（2-1）と当然一致します。
（2-5）式はつり合いの式ですが、(2-2)の運動方程式と一致しています。

 

　つまり、慣性力を導入することによって、線路に静止している観測者が観測しても、電車の中にいる観測者が観測しても、同じ結果（式）が得られることがわかりました。
観測者が電車の中にいると書きましたが、電車の外にいて電車と同じ運動（加速度\(\alpha\)の定加速度運動）をしていれば、電車の中にいる観測者と同じ観測結果が得られます。

 

 

 

 

２．運動方程式と遠心力-（１）

 

 

　図1-1をもう一度図2-8として再掲します。
この図は宇宙空間から地球と人工衛星の両方を眺めた図です。

 

　どこから眺めているかを厳密に考えるのは難しいですが、通常の問題では、慣性系から観察していることになります。
慣性系とは、観察対象の物体や系に運動の法則が成り立つ系ですから、実際にはたらく力を元に「運動の法則」を使って問題を解くことができます。

 

 

　さて、図2-8で人工衛星にはたらく力は万有引力だけです。
宇宙から見れば、人工衛星は万有引力によって常に地球の重心に向かって加速されるように力を受けている、と認識できます。

 

　したがって、この観察者の立場では、円運動の運動方程式を立てることができて、
\begin{eqnarray} m\frac{v^2}{R}=G\frac{mM}{R^2} \tag{2-6} \\
mR\omega^2=G\frac{mM}{R^2} \tag{2-7}
\end{eqnarray}
となります。

 

 

 

 

 

　次に、人工衛星に乗った観測者が観測する場合について考えてみます。観測者は人工衛星に乗っていなくても、観測者自身が人工衛星と同じ円運動をしていれば以下の内容と同じことが言えます。

 

　このとき、観測者には人工衛星と地球の距離は変化していないと認識します。
　しかし、地球と人工衛星の間には万有引力がはたらいています。しかも、地球の質量が圧倒的に大きいので、人工衛星は地球に引き寄せられるはずですが、人工衛星と地球の距離は変わらないのですから、観測者はおかしいと考えます。

 

 

　この観測者は加速度運動をしているので、座標系は非慣性系です。このため、観測結果が運動の法則に反するように見えます。
これを解消するには、「１．観測する立場の違いについて」で述べたように、慣性力を導入します。
この例のように物体とともに円運動する立場から見たときの慣性力を、特に遠心力と言います。
遠心力は慣性力のひとつであり、"みかけの力"です。

 

 

 

 

　遠心力による加速度の大きさと、観測者が受けている加速度（つまり、向心力による加速度）の大きさは同じで、向きはその逆です。
つまり、遠心力の大きさは、[人工衛星の質量]×[観測者が感じる（向心力による）加速度]です。
人工衛星の質量は\(m\)、速さが\(v\)、角速度が\(\omega\)で、円運動の半径が\(R\)であるとすれば、遠心力は\(m\frac{v^2}{R}=mR\omega^2\)と表されます。
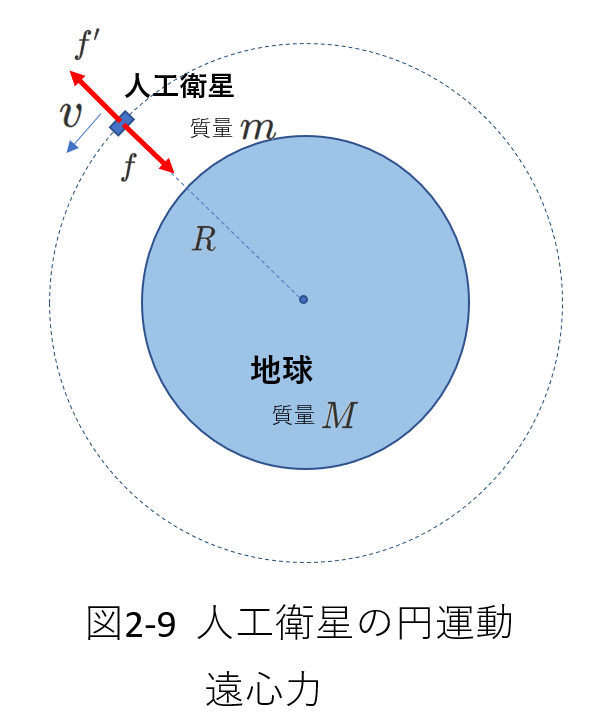
この例について、遠心力を表した図を描くと、右図2-9となります。

 

　人工衛星にはたらいている力は、万有引力\(f\)と遠心力\(f'\)です。
これがつりあっているので、人工衛星は静止しているように見えます。
遠心力を用いてつり合いの式を立てると、
\begin{eqnarray} f'=f \tag{2-8} \\
m\frac{v^2}{R}=G\frac{mM}{R^2} \tag{2-9} \\
mR\omega^2=G\frac{mM}{R^2} \tag{2-10}
\end{eqnarray}

 

　この例では、（2-9）（2-10）式は(2-6)(2-7)式と一致します。
どのような円運動でも円運動の運動方程式と遠心力を用いたつり合いの式とは同値になりますが、
ふたつの立場の違いによって、最初に立てる式の形が少し異なることがあります。
それを次の例で示します。

 

 

 

 

３．運動方程式と遠心力-（２）

 

　右図で、他方が円錐台の頂点に固定された、長さ\(l\)の糸につながれた質量\(m\)のおもりが円錐台に沿って速さ\(v\)で円運動をしています。

 

　この円運動の運動方程式を立て、おもりにはたらく力を求めます。

 

　おもりと円錐台の表面の間に摩擦はありません。
また、運動中に糸が弛むことはなく、円錐台は水平面上に立っていて、おもりの大きさは無視できるものとします。

 

 

　最初にすることは、おもりにはたらく力を漏れなく図示することです。

 

　おもりにはたらく力は、重力\(mg\)、
それから、接触しているところには必ず力がはたらくことに注目して、糸の張力\(T\)と円錐台からの垂直抗力\(N\)です。
（それぞれの文字は力の大きさを表しています。）

 

　次に運動について考えます。

 

　運動は、円錐台に沿った円運動ですから、円運動自身は水平面に沿った運動で、鉛直方向の運動はありません。
このことから、力の合力の鉛直成分は\(0\)です。
（力の鉛直成分はつりあっている、とも表現できます。）

 

　さて、円運動について、
　円運動の中心は、点Oです。
したがって、円運動の半径は、\(l\sin\theta\)です。
（半径を\(l\)と勘違いしないようにしましょう。）

 

　おもりの質量\(m\)、速さ\(v\)、半径\(l\sin\theta\)で、あと、向心力を数式化できれば運動方程式が立てられます。
向心力は、円運動の中心方向にはたらく力で中心に向かう向きが正です。
図2-10の力の図から、向心力になる力は、張力\(T\)の水平方向成分と垂直抗力の水平方向成分だとわかります。

 

　以上より、運動方程式は、
\begin{equation} m\frac{v^2}{l\sin\theta}=T\sin\theta-N\cos\theta \tag{2-11} \end{equation}
　また、力の鉛直成分のつりあいを考えると、
\begin{equation} mg=T\cos\theta+N\sin\theta \tag{2-12} \end{equation}

 

　方程式が2つになったので、張力\(T\)と\(N\)を求めることができます。

 

　\(T\)を求めるために、（2-11）×\(\sin\theta\) + （2-12）×\(\cos\theta\)を計算します。
\begin{eqnarray} T\sin^2\theta-N\cos\theta\sin\theta&=&m\frac{v^2}{l} \tag{2-13} \\
T\cos^2\theta+N\sin\theta\cos\theta&=&mg\cos\theta \tag{2-14} \\
(2-13)+(2-14)より、 T&=&m\frac{v^2}{l}+mg\cos\theta=m\left(\frac{v^2}{l}+g\cos\theta\right) \tag{2-15} \\
(2-11)より、　　N\cos\theta&=&T\sin\theta-m\frac{v^2}{l\sin\theta} \tag{2-16} \\
&=&m\left(\frac{v^2}{l}+g\cos\theta\right) \sin\theta-m\frac{v^2}{l\sin\theta} \\
N&=&m\frac{v^2\sin\theta}{l\cos\theta}+mg\sin\theta-m\frac{v^2}{l\sin\theta\cos\theta} \\
&=&m\frac{v^2\sin^2\theta-v^2}{l\sin\theta\cos\theta}+mg\sin\theta \\
&=&m\frac{-v^2\cos^2\theta}{l\sin\theta\cos\theta}+mg\sin\theta \\
&=&m\left(g\sin\theta-\frac{v^2}{l\tan\theta}\right) \tag{2-17}
\end{eqnarray}

 

　検証してみます。
（2-15）（2-17）式で\(\theta=\frac{\pi}{2}\)としてみます。
この状態では、円錐台は円盤のようなものと考えられます。
\begin{eqnarray} T=m\frac{v^2}{l} \\
N=mg
\end{eqnarray}
となります。これは、水平面上の円運動の場合の値と一致します。

 

 

 

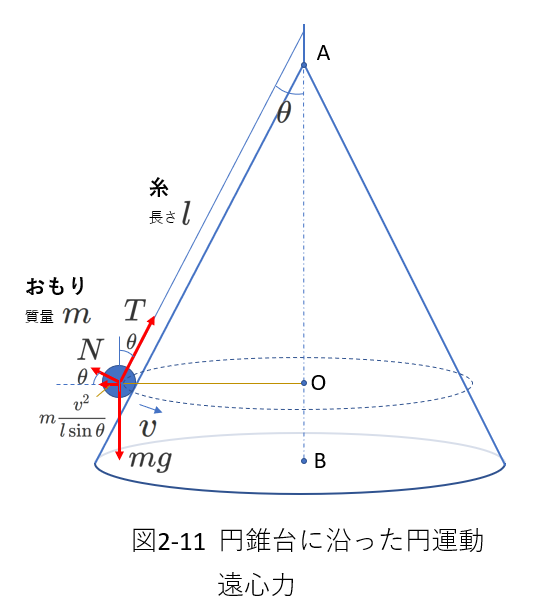
　次に、遠心力を使って考えてみます。
遠心力で考えるということは、観測者はおもりと同じ（点Oを中心とする）円運動をしています。

 

　右図2-11に示すように、おもりにはたらく力に遠心力が加わります。

 

　遠心力は慣性力ですから、向心力による加速度と逆の向き（すなわち、円運動の中心と逆の向き）にはたらきます。
観測者はおもりと同じ（点Oを中心とする）円運動をしているわけですから、おもりは静止しているように見えます。
つまり、力がつりあっているように見えます。

 

　そこで、力の水平方向成分と鉛直方向成分のつり合いを考えて、式を立てると、次のようになります。
\begin{eqnarray} m\frac{v^2}{l\sin\theta}+N\cos\theta&=&T\sin\theta \tag{2-18} \\
mg&=&T\cos\theta+N\sin\theta \tag{2-19}
\end{eqnarray}　
　\(m\frac{v^2}{l\sin\theta}\)が遠心力です。
　運動方程式（2-11）式とつり合いの式（2-18）式とは同値です。
しかし、考え方の違いに基づき、微妙に式の形が異なることを確認してください。

 

 

 

　ところで、この問題では\(v\)がある範囲にあればおもりは円錐台に沿って円運動をします。
（2-15）（2-17）式を見ると、\(v\)が小さければ、張力\(T\)は小さく垂直抗力\(N\)は大きいです。
\(v\)が大きくなると、張力\(T\)は増加し、垂直抗力\(N\)は減少します。
さらに\(v\)が大きくなると、垂直抗力\(N\)は負になってしまいます。
これは何を意味するのでしょうか。

 

　一般的に、\(垂直抗力\lt 0\)はおもりが円錐台から離れることを意味します。
逆に言えば、おもりが円錐台から離れる条件は、\(垂直抗力\lt 0\)から求めます。

 

　（2-17）式の元の式（2-16）式を見てください。
この式に、\(N\lt 0\)を適用すると、（2-16）式から、
\begin{equation} T\sin\theta\lt m\frac{v^2}{l\sin\theta} \tag{2-20} \end{equation}
が、得られます。
　この式は、［張力の水平成分（つまり、おもりを円運動の中心に向かって円錐台の壁に押し付けようとする力）］ < ［遠心力（おもりを中心から逆向きに、円錐台の壁から離そうとする力］を意味していますから、この条件でおもりが円錐台から離れることが理解できます。

 

　（2-16）式と（2-17）式は同値のはずですから、（2-17）式に\(N\lt 0\)を適用してみます。すると、次のようになります。
\begin{eqnarray} mg\sin\theta\lt m\frac{v^2}{l\sin\theta}\times \cos\theta \tag{2-21} \\
v^2\gt gl\sin\theta\tan\theta \tag{2-22}
\end{eqnarray}
(2-21)式は（2-20）式と随分違いますが、（2-21）式は、［重力の円錐台の壁に垂直な成分で円運動の内向きの力］ < ［遠心力の円錐台の壁に垂直な成分で円運動の外向きの力］を意味しています。
この式についても、この条件でおもりが円錐台から離れることが納得できます。

 

　おもりが円錐台の壁から離れるとき、垂直抗力が\(0\)から負になります。
　注）式の上で負になるということであり、実際には、おもりが円錐台の壁から離れれば、
　　　もはや垂直抗力ははたらかないわけですから、その大きさは0です。

 

　（2-20）（2-21）式で確認したように、このとき遠心力の大きさは、おもりに円運動の内向きにはたらく力よりも大きくなります。
　したがって、垂直抗力の正負からではなく、遠心力とおもりに円運動の内向きにはたらく力の大小関係からも、おもりが離れる条件を求めることができるのですが、この時にはふたつの力は同じ方向の成分で考える必要があります。

 

 

１．鉛直面内の円運動の例１

 

　

　右図3-1で、右側半分は内面が半円筒形状にくりぬかれた直方体の物体で、それが点Aで物体の内面と床の表面が滑らかにつながっています。

 

　図は半円筒の主軸に垂直な面での、床および物体の断面を示していて、床上を速さ\(v_0\)で進む、質量\(m\)の小球は、この断面図が示す平面上で運動をするものとします。
　小球は、点Aで右側の物体に侵入し点Bから点Cと、半径\(r\)の円運動をします。
小球の大きさは無視でき、小球と小球が進む表面との間には摩擦はないものとします。

 

ここで、小球が点Cに達するための\(v_0\)が満たすべき条件を求めます。

 

　図3-1の断面は、鉛直面（鉛直方向に平行な面）で、小球はこの面内で円運動をします。
鉛直面内で円運動をする場合は、等速円運動ではなく、非等速円運動となります。

 

　力学の問題で最初に行うことは、物体にはたらく力を漏れなく数え上げ、それを図示することです。
小球にはたらく力を図示すると、図3-2のようになります。

 

 

　この図で、小球が点Dにある場合と点Eにある場合について図示しています。
この系の外部から見た場合、小球にはたらいている力は、重力（\(mg\)）と小球が接している面から受ける垂直抗力（\(NまたはN'\)）です。

 

　次に、保存則について検討します。

 

　小球の力学的エネルギー保存について、小球にはたらいている力を元に考えます。

 

・重力は保存力ですから、小球に重力だけがはたらいている状態では力学的エネルギー保存則は成り立ちます。

 

・垂直抗力は非保存力です。非保存力がはたらいている物体では力学的エネルギーは保存されません。
　しかし、詳しく見ると、垂直抗力と小球の進む向きとは垂直です。
　したがって、垂直抗力は小球に対して仕事をしません。言い換えると、垂直抗力は小球の運動エネルギーを変化させません。

 

　以上まとめると、非保存力がはたらいているけれども、小球について力学的エネルギーが保存されることがわかります。

 

 

　小球の運動量保存について、小球にはたらいている力を元に考えます。
小球にはたらく重力は外力ですから、一般的に運動量は保存されません。
　垂直抗力については、点Aまでの床上を滑っている間は、垂直抗力と重力がつりあっていて合力は\(0\)ですから、運動量は保存されます。つまり、この場合は、小球の速度は変わらないということです。
　しかし、A⇒B⇒Cの間では、重力により小球の速度は変化するので、運動量は保存されません。

 

（ここでは敢えて小球の運動量の保存について考えましたが、通常、対象が1個の場合、運動量保存を検討する必要はありません。この場合に運動量が保存されることは、小球が静止、あるいは、等速度運動をする、ことだからです。）

 

 

　小球について力学的エネルギー保存の式を立てます。

 

　点Dでの小球の速さを\(v\)として、重力による位置エネルギーの基準を床表面とします。
また、\(\angle {AOD}\)をOAから左回りに測定して、\(\theta\)とします。
\begin{equation} \frac{1}{2}mv_0^2=\frac{1}{2}mv^2+mgr(1-\cos\theta) \tag{3-1} \end{equation}
　ここで、床から天Dまでの高さが\(r(1-\cos\theta)\)で表されることを確認してください。
　また、（3-1）式を\(v\)について解けば、
\begin{equation} v=\sqrt{v_0^2-2gr(1-\cos\theta)} \end{equation}
となり、\(\theta\)が変化すれば\(v\)が変化し、\(0\leqq \theta \leqq \pi\)の範囲で\(\theta\)の増加により\(v\)が減少することがわかります。
これは、小球の高さが高くなることで運動エネルギーが重力による位置のエネルギーに変化するためです。

 

　ちなみに、点Eでの力学的エネルギー保存の式を立ててみます。
床から点Eまでの高さは、\(r(1-\cos\theta')\)です。
角AOEもAOから左回りに測定して\(\theta'\)としています。
点Eでの小球の速さを\(v'\)とすれば、力学的エネルギー保存則は、
\begin{equation} \frac{1}{2}mv_0^2=\frac{1}{2}mv'^2+mgr(1-\cos\theta') \tag{3-2} \end{equation}

 

　（3-1）式と（3-2）式を比べると、ダッシュ「'」があるなし以外は同じであることがわかります。
このことは、点A-D-B-E-Cの任意の点で、小球の速さを\(v\)、AOからの角度を\(\theta\)とすれば、（3-1）式の力学的エネルギー保存の式が成り立つことを意味しています。

 

 

　小球が点Cに到達する条件は、点Cにおいて小球の速さ\(v\)が正、言い変えれば\(v\)が実数、または、運動エネルギー\(\frac{1}{2}mv^2\geqq 0\)です。　（3-1）式から
\begin{eqnarray} \frac{1}{2}mv^2=\frac{1}{2}mv_0^2-mgr(1-\cos\theta)\geqq 0 \tag{3-3} \\
\frac{1}{2}mv_0^2\geqq mgr(1-\cos\theta) \\
v_0\geqq \sqrt{2gr(1-\cos\theta)} \\
点Cでは\theta=\piであること、また、このとき上式の右辺が最大になることから、\\
v_0\geqq 2\sqrt{gr} \tag{3-4} \\
\end{eqnarray}
となります。

 

　さて、（3-4）式の条件で十分でしょうか？
このことを考えるために、下の図に小球に対して力学的エネルギーが保存される3つの場合をあげてみました。いずれも摩擦ははたらかないとします。比較してみましょう。

 

　(a)は本例題です。
　(b)は傾斜角が一定な斜面台を小球が滑りあがります。
小球にはたらく力は、重力と垂直抗力で、どちらも時間に依らず一定です。
したがって、運動は等加速度運動で、垂直抗力は常に小球の進行方向に対して垂直ですから、小球の加速度は重力の斜面方向の成分で決まります。
小球の最初の運動エネルギー\(\frac{1}{2}mv_0^2\)がすべて位置エネルギーに変わって、運動エネルギーが\(0\)になるまで斜面を登ります。

 

 

　(c)では、斜面を登った途中で、空中に飛び出します。
斜面台を離れたあと、小球にはたらくのは重力だけです。
この運動は放物運動、鉛直方向に加速度\(-g\)の等加速度運動、水平方向には等速度運動をします。
水平方向には常に一定速度ですから、運動エネルギーが\(0\)になることはありません。
小球が最も高く上がったところで運動エネルギーが最小になります。

 

　(a)の場合には(b)(c)と異なり、点Cで重力だけでなく垂直抗力も下向きにはたらきます。
点Cで小球の速度がちょうど\(0\)になったと仮定した場合、このとき遠心力も\(0\)になりますから、重力と垂直抗力は円筒内面から小球を引きはがす向きにはたらくことになり、点Cに達するのは難しそうです。
（遠心力を用いた立式については後述しますが、遠心力で考えた方が理解しやすいので、ここで遠心力を持ち出しました。）

 

 

　さて、もとに戻って、（3-1）式の力学的エネルギー保存の式を立てるときの条件をもう一度吟味してみましょう。
垂直抗力は小球の進む向きに垂直であるから力学的エネルギーが保存されると考えました。
つまり、小球が円筒の内面に沿って運動するということを前提として立式しています。

 

　では、途中で内面から離れた場合はどうなるのでしょうか。
離れれば、小球にはたらく力は重力だけになりますから、それ以後も力学的エネルギーは保存されます。
しかし、(c)の場合のように水平方向には等速度運動になり、運動エネルギーが\(0\)になることはありません。
したがって、離れた場合には、（3-4）式の等号が成立する条件では、点Cまで達することができません。

 

　以上より、小球が点Cまで内壁面から離れない条件を検討する必要があることがわかります。

 

　小球が壁から離れない条件は\(垂直抗力\geqq 0\)です。
そして、垂直抗力を求めるには円運動の運動方程式を、用います。
これと、(3-1)式を連立して垂直抗力を求めることができます。
（3-1）式から\(v\)を求め、それを円運動の運動方程式を使って垂直抗力を求めます。
点Dで考えると、円運動の運動方程式は、
\begin{equation} m\frac{v^2}{r}=N-mg\cos\theta \tag{3-5} \end{equation}
となります。
　（3-5）式では、\(\theta\)が変化すると、\(v\)も\(N\)も変化することに注意しましょう。
この点が水平面内の円運動の場合と異なるところです。

 

 

 

 

　続いて（3-1）式から\(v\)を求めます。
\begin{equation} v^2=v_0^2-2gr(1-\cos\theta) \tag{3-8} \end{equation}
これを(3-5)式に代入して\(N\)を求めます。
\begin{eqnarray} N&=&m\frac{v^2}{r}+mg\cos\theta \\
&=&\frac{m}{r}\{v_0^2-2gr(1-\cos\theta)\} +mg\cos\theta \\
&=&m\frac{v_0^2}{r}-2mg+3mg\cos\theta \tag{3-9}
\end{eqnarray}
\(N\geqq 0\)を適用すると、
\begin{eqnarray} N=m\frac{v_0^2}{r}-2mg+3mg\cos\theta\geqq 0 \\
m\frac{v_0^2}{r}\geqq 2mg-3mg\cos\theta \\
\theta=\piですから、
m\frac{v_0^2}{r}\geqq 5mg \\
v_0\geqq\sqrt{5gr} \tag{3-10}
\end{eqnarray}

 

　（3-4）式と比較すると、（3-10）式を満たせば小球は点Cに到達できることがわかります。

 

 

 

 

　次に、遠心力を使って考えてみましょう。

 

　観測者が小球の円運動とともに運動するときには、小球は静止しているように見えるので、この立場では力のつりあいを考えます。
注意することは、観測者自身が加速度運動をしているので、慣性力を加えて力のつりあいを考える必要があります。
円運動は仮に等速であっても加速度運動で、このときの慣性力は遠心力と呼ばれます。

 

　遠心力を加えて、小球にはたらく力を図示すると、図3-4のようになります。

 

　点D、E、Cで点Oから離れる向きの赤い実線の矢印がそれぞれの点での遠心力を表しています。
点Cでは、小球の速さが\(v''\)で、垂直抗力が\(0\)、すなわち、遠心力=重力の状態にあるとして図を描いています。

 

点Dでの力のつりあいを考えると、
\begin{equation} N=mg\cos\theta+m\frac{v^2}{r} \tag{3-11} \end{equation}
　（3-5）式と同値の式になりました。

 

点Eでの力のつりあいを考えると、
\begin{equation} N'+mg\cos\theta''=m\frac{v'^2}{r} \tag{3-12} \end{equation}
　（3-6）式と同値の式になりました。

 

　このように、遠心力を考えても、前述の円運動の運動方程式を考えた場合と全く同じように解くことができます。

 

 

　点Cについてもう少し考えます。
　点Cで小球が壁を離れる寸前という状態を考えると、このとき垂直抗力=\(0\)です。
つまり、重力と遠心力がつり合っています。

 

　したがって、
\begin{eqnarray} m\frac{v''^2}{r}=mg \tag{3-13} \\
v''=\sqrt{gr} \tag{3-14}
\end{eqnarray}

 

　つまり、 点Cで\(v''=0\)と考えて求めた（3-4）の条件では十分ではないことがわかります。
遠心力を使った図3-4を参照すると、このことを理解しやすいです。

 

　敢えて言えば、点Cで\(垂直抗力\geqq 0\)の条件を考えるのであれば、このとき\(遠心力\geqq 重力\)、ゆえに\(v\gt 0\)であることがわかりますから、（3-3）式の条件を考える必要がなかったということがわかります。

 

 

 

 

 

 

 

　２．鉛直面内の円運動の例２

 

 

 

　右図3-5で、半径が\(r\)の半球が床の上に伏せて固定され、その頂点に質量\(m\)の小球が置かれています。
今、小球が静かに球の表面を滑り始めます。
図3-5は、頂点を含む鉛直面で切った半球の断面を示しています。
小球はその断面の稜線に沿って図のように半球の表面を滑り降りていきます。
小球と半球の間には摩擦はないとします。

 

　小球が半球の表面から離れるときの、小球と球の中心を結ぶ線分と鉛直方向とのなす角度（図で\(\theta\)）を求めます。
実際には、\(\theta\)の値ではなく、\(\cos\theta\)を求めます。

 

　今図のように、小球がBにあるときの\(\angle {AOB}\)を\(\theta\)、速さを\(v\)とします。

 

　最初に行うことは、（小球の運動を議論するのですから）小球にはたらく力をすべて数え上げることです。
図3-5に示したように、床に立って見たとき、小球にはたらく力は、重力\(mg\)と(半球に接触しているので）半球から受ける垂直抗力です。円運動の向心力は、\(mg\cos\theta-N\)であることがわかります。

 

　さて、「小球が半球から離れる」ことは何故起こるのでしょうか。
円運動は、運動する物体が向心力により常に円運動の中心に加速されることで維持されます。
向心力がなくなれば、小球はそのときの運動の接戦方向に進みます。
慣性の法則により常に接線方向に直線運動しようとする小球を、向心力が円の中心に向かうようにしていると捉えられます。

 

　円運動を維持するのに必要な向心力の大きさは\(m\frac{v^2}{r}\)です。
小球が半球を滑り落ちるのに連れて、重力による位置エネルギーが運動エネルギーに変わり、小球の速さが増加します。
したがって、円運動の維持に必要な向心力も増加するわけですが、その向心力\(mg\cos\theta-N\)を構成する\(mg\cos\theta\)は減少するわけですから、
\(v\)が増したどこかの時点で小球が半球表面から離れることが起こります。

 

 

　さて、小球の運動は鉛直面内の円運動ですから、力学的エネルギー保存則と円運動の運動方程式を考えるのが定石です。

 

　小球には、保存力である重力のほかに、非保存力である垂直抗力がはたらきますが、垂直抗力は小球の進む向きに対して垂直にはたらくので、小球に対して仕事をしません。
したがって、小球について力学的エネルギーが保存されます。

 

　力学的エネルギー保存の式から\(v\)が求められ、その結果と円運動の運動方程式から垂直抗力\(N\)が求められます。
そして、「小球が半球表面を離れる直前」には、「垂直抗力\(=0\)」であると考えます。

 

 

　重力による位置エネルギーの基準を床面とします。
「点Aで静止している小球の力学的エネルギー」=「点Bでの力学的エネルギー」という力学的エネルギー保存の式を立てます。
\begin{eqnarray} \frac{1}{2}m\times 0^2+mgr&=&\frac{1}{2}mv^2+mgr\cos\theta \tag{3-15} \\
これより、v&=&\sqrt{2gr(1-\cos\theta)} \tag{3-16}
\end{eqnarray}

 

　点Bにおける円運動の運動方程式は、
\begin{eqnarray} m\frac{v^2}{r}&=&mg\cos\theta-N \tag{3-17} \\
(3-16)を代入すると、N&=&mg\cos\theta-m\frac{v^2}{r} \\
&=&mg\cos\theta-2mg(1-\cos\theta) \\
&=&-2mg+3mg\cos\theta
\end{eqnarray}
　\(N=0\)として、
\begin{eqnarray} N=-2mg+3mg\cos\theta=0 \\
\cos\theta=\frac{2}{3} \tag{3-18}
\end{eqnarray}

 

 

 

 

 

 

　次に、遠心力を使って考察します。

 

　小球に乗った観測者から、あるいは、小球と同じ円運動をする観測者から小球の運動を考えたとき、小球は静止しているように見えます。
　したがって、小球にはたらく力はつりあっていると考えます。

 

　ただし、観測者自身が加速度運動をしているので、慣性力である遠心力を導入して、重力・垂直抗力・遠心力がつりあっていると考えます。

 

　式に表せば、
\begin{equation} mg\cos\theta=N+m\frac{v^2}{r} \tag{3-19} \end{equation}
となり、（3-17）式と同値の式が得られました。

 

　遠心力から、「小球が半球から離れる」ことを説明してみます。

 

　小球にはたらく力のうち重力は、半球の中心向きの成分\(mg\cos\theta\)が小球を半球に押し付けるようにはたらき、半球の接戦方向成分の\(mg\sin\theta\)は小球を半球に沿って下向きに加速させるようにはたらきます。
　一方、遠心力は小球を半球から引き離すようにはたらきます。
小球が半球に接している間は、\(mg\cos\theta\)と遠心力の差に等しい大きさの垂直抗力がはたらいて、3つの力がつりあいます。
\(\theta\)（したがって、\(v\)）が、大きくなるにつれ、遠心力が大きく、\(mg\sin\theta\)が小さくなります。
遠心力が\(mg\cos\theta\)より大きくなれば小球は半球から離れます。
つまり、離れる直前に、遠心力と\(mg\sin\theta\)が等しくなるはずですから、
\begin{eqnarray} m\frac{v^2}{r}=mg\cos\theta \\
（3-16）式のvを代入して、m\frac{2gr(1-\cos\theta)}{r}=mg\cos\theta \\
2(1-\cos\theta)=\cos\theta \\
\cos\theta=\frac{2}{3}
\end{eqnarray}
　（3-18）と同じ結果になりました。

 

 

 

１．例題１

 

　穴の空いた質量\(m\)のおもりを針金にとおし、その針金を曲げて半径\(R\)の円環を作ります。

 

　この円環に軸をつけて、図4-1のように軸の周りに円環が自由に回転できるように、床に軸を差し込みます。　
おもりの軸は仮想的なもので、おもりが針金に沿って自由に動くことを妨げないものとします

 

　針金とおもりの間に摩擦はありません。
　また、おもりの位置を、図のようにおもりと円環の中心を結ぶ線分の鉛直下向きからの角度\(\theta\)で表します。
そして、反時計廻りの向きを\(\theta\)の正の向きとします。

 

　さて、おもりを角度\(\theta\)のAの位置に支持し、円形の針金を軸のまわりに角速度\(\omega\)で回し、支持を外したところ、おもりは\(\theta\)の位置から動きませんでした。このときのおもりの位置（\(\cos\thetaの値\)）を求めます。

 

 

　最初におもりにはたらく力を確認します。
重力\(mg\)がはたらきます。
そして、おもりは針金に接しているので、ここから垂直抗力を受けます。
垂直抗力をどちら向きに受けるでしょうか。

 

　おもりは\(O'\)を中心として針金と同じ角速度\(\omega\)で円運動をしています。
したがって、向心力がはたらいています。
向心力の向きは、おもりから円運動の中心を向く向き（A→O'の向き、つまり図4-1では水平方向左向き）です。
（ここで、O'はおもりの位置Aから回転軸に降ろした垂線の足です。）
したがって、重力が向心力になることはなく、垂直抗力のA→O'向きの成分が向心力の役割をしていると考えるのが妥当です。

 

　また、垂直抗力は針金に対して垂直の向きになるはずですから、これらを考えあわせると、垂直抗力の向きはA→Oの向きであることがわかります。
（Oは、針金の円環の中心です。）

 

　さて、おもりは角速度\(\omega\)の円運動をしています。
そして、垂直抗力\(N\)の水平成分\(N\sin\theta\)が円運動の向心力です。
また、\(\theta\)が変化しないことから、鉛直方向の力はつりあっていると考えられます。

 

　未知数は、問われている\(\theta\)と垂直抗力\(N\)となると予想され、方程式が2つ立てられるので、連立して\(\theta\)を求められそうです。
計算してみましょう。

 

　円運動の運動方程式と鉛直方向の力のつりあいの式はそれぞれ次のようになります。
\begin{eqnarray} m(R\sin\theta)\omega^2&=&N\sin\theta \tag{4-1} \\
N\cos\theta&=&mg \tag{4-2}
\end{eqnarray}
(4-2)式より、\(N=\frac{mg}{\cos\theta}\)、これを（4-1）式に代入して、両辺を\(\sin\theta\)で割るなどして、
\begin{eqnarray} mR\omega^2&=&\frac{mg}{\cos\theta} \\
\cos\theta&=&\frac{g}{R\omega^2} \tag{4-3}
\end{eqnarray}
が、得られました。

 

 

 

 

　　

　次に、回転する針金と同じ運動をする観測者から、式を立ててみます。
観測者自身が加速度運動をしているので、観測しているおもりには慣性力である遠心力がはたらいていると考えます。
この遠心力の大きさは、\(m(R\sin\theta)\omega^2\) です。
（円運動の半径は\(R\)ではなく、\(R\sin\theta\)であることに注意しましょう。）
おもりにはたらく力を図4-2に示します。

 

 

　観測者からはおもりは静止しているように見えるので、力のつりあい（または、合力\(=0\)）を考えます
運動方程式で解いたときに考えた方向に替えて、針金の円環に沿った方向（円環の接線方向）とそれに垂直な方向の成分について力のつり合いの式を考えます。
\begin{eqnarray} m(R\sin\theta)\omega^2\times \cos\theta=mg\sin\theta \tag{4-4} \\
N=mg\cos\theta+m(R\sin\theta)\omega^2\times \sin\theta \tag{4-5}
\end{eqnarray}

 

　上式を見ればわかりますが、（4-4）式には未知数の\(N\)は含まれていません。

 

　したがって、（4-4）式だけから\(cos\theta\)の値を求めることがでて、
\begin{eqnarray} m\sin\theta(R\omega^2-\frac{g}{\cos\theta})=0 \\
これより、\sin\theta=0　または、\cos\theta=\frac{g}{R\omega^2}
\end{eqnarray}　
　前述の結果に一致しました。

 

 

 

 

 

 

 

 

 

　２．例題２

 

 

　例題１と似た問題です。
　右図4-6で、まっすぐな棒\(OA\)が水平面から角度\(\theta\)で自由に回転する鉛直な棒\(OO'\)に接続されています。
今\(OO'\)が角速度\(\omega\)で回転していて、棒\(OA\)も同じ角速度で回転しています。
棒には穴が開いた質量\(m\)のおもりがとおされています。
　例題２と異なり、棒とおもりの間には摩擦がはたらくものとします。

 

　おもりも角速度\(\omega\)で\(OO'\)の周りを回転していますが、おもりの棒に対する位置が変化しないときRが満たすべき条件を求めます。
　なお、棒とおもりの間の摩擦の静止摩擦係数を\(\mu_0\)とします。

 

 

　この問題を解くにあたって、観測者はおもりとともに運動をしていると仮定します。
つまり、慣性力である遠心力がはたらくとして考察をします。

 

　最初にすることは、おもりにはたらく力を漏れなく図示することです。
図4-6に力を図示しました。
図に記した文字はいずれも力の大きさを表しています。

 

　おもりには、重力・棒からの垂直抗力・遠心力・棒からの摩擦がはたらきます。
観察者にはおもりは静止して見えますから、この4つの力はつりあっていると考えます。

 

　重力（大きさ\(mg\)）は鉛直方向下向きにはたらきます。
　棒からの垂直抗力は、平面\(O'OA\)に平行、かつ棒\(OA\)に垂直にはたらきます。
重力、遠心力、摩擦力のいずれも、\(OA\)に垂直で上向きの成分をもたないので、これらの力と釣り合うためには、垂直抗力は上向きであると考えます。
遠心力は回転軸に垂直で、右図では水平右向き（回転軸から外向き）です。

 

　難しいのは摩擦力です。
摩擦力が、棒の長さ方向にはたらくのはわかりますが、上向きか下向きかがわかりません。
そこで、図4-6では、おもりが棒と及ぼし合う摩擦力の大きさを\(f\)として、仮に上向きであると仮定して図示しました。

 

 

　次にそれぞれの力の関係を想像してみます。
　①摩擦がない場合、重力の棒の長さ方向成分が遠心力の棒の長さ方向の成分よりも大きければ、おもりは棒をずるずると滑り降ります。
このとき摩擦が図と同じように棒の長さ方向に沿って上向きにはたらけば、そしてその摩擦力の大きさが最大静止摩擦力よりも小さければ、おもりはずり落ちずに済みます。　

 

　②この逆に、摩擦がない場合に、重力の棒の長さ方向成分が遠心力の棒の長さ方向の成分よりも小さければ、おもりは棒をずるずると這い上がります。
このとき、おもりが棒上の同じ位置にいるためには、ふたつの力の棒方向成分の差と同じ大きさの静止摩擦力（かつ、最大静止摩擦力以下）が下向きにはたらくことになります。　

 

　図4-6を参照して、棒に沿った方向の力のつりあいを式に表します。
\begin{eqnarray} f+mR\omega^2\cos\theta&=&mg\sin\theta \tag{4-26} \\
f&=&mg\sin\theta-mR\omega^2\cos\theta \tag{4-27} \\
\end{eqnarray}

 

 

　さて、（4-27）式が成立すれば力のつりあいが成り立ち、おもりは棒に対して静止することになります。
ただし、①②で考えたように、\(f\)が最大静止摩擦力以下という条件が付きます。

 

　つまり、上で説明したように、\(f\)は正負両方の値を取り得るとすれば、
\begin{eqnarray} |f|&\leqq& \mu_0 N \tag{4-30} \\
書き換えれば、&&-\mu_0 N\leqq f\leqq \mu_0 N \tag{4-31}
\end{eqnarray}

 

　したがって、\(N\)を求める必要があります。
そのためには、棒に垂直な方向の力のつりあいを考えます。
図4-6を参照して、
\begin{equation} N=mg\cos\theta+mR\omega^2\sin\theta \tag{4-32} \end{equation}

 

　（4-32）式と（4-31）（4-27）式から
\begin{eqnarray} -\mu_0(mg\cos\theta+mR\omega^2\sin\theta) \leqq mg\sin\theta-mR\omega^2\cos\theta \leqq \mu_0(mg\cos\theta+mR\omega^2\sin\theta) \tag{4-33} \\
つまり、-\mu_0(mg\cos\theta+mR\omega^2\sin\theta) \leqq mg\sin\theta-mR\omega^2\cos\theta　\tag{4-34} \\
かつ、mg\sin\theta-mR\omega^2\cos\theta \leqq \mu_0(mg\cos\theta+mR\omega^2\sin\theta)　\tag{4-35}
\end{eqnarray}
となります。

 

　(4-34)(4-35)式をRについて整理します。
(4-34)式から、
\begin{eqnarray} mR\omega^2(\cos\theta-\mu_0\sin\theta)\leqq mg(\sin\theta+\mu_0\cos\theta) \\
R\leqq \frac{g(\sin\theta+\mu_0\cos\theta)}{\omega^2(\cos\theta-\mu_0\sin\theta)} \tag{4-36} \\
ただし、\cos\theta-\mu_0\sin\theta　としました。 \tag{4-37}
\end{eqnarray}
(4-35)式からは、
\begin{eqnarray} mR\omega^2(\cos\theta+\mu_0 \sin\theta) \geqq mg(\sin\theta-\mu_0 \cos\theta) \\
R\geqq \frac{g(\sin\theta-\mu_0\cos\theta)}{\omega^2(\cos\theta+\mu_0\sin\theta)} \tag{4-38}
\end{eqnarray}
　「（4-36）かつ（4-38）式」が求める条件です。
求める際には（4-37）式を仮定しました。
　実際の問題では、\(\theta\)が具体的に決まっていたり、\(\theta\)と\(\mu_0\)との関係が指定されていたりするはずですから、ここでは、(4-37)式が成立しない場合についての考察を省略しました。

 

関連ページ

作図

物理の問題を解く場合、図を描くことは必須と言えます。図を活用することで、考察が進み、その結果ミスを減らすことができます。図を活用する場合の注意点を説明しています。

運動方程式

物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。

モーメントの考え方

力のモーメントについて、基本的注意事項のいくつかを説明しています。

運動量保存則を使う問題

運動量保存則は、力学でも最も重要な概念のひとつです。運動量が保存される場合と保存されない場合について説明し、例題を掲げました。

張力

糸につながれたおもりの運動では、糸の張力を考慮します。張力を考える場合のヒントを説明しています。

運動エネルギーと仕事の関係

運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。

力学的エネルギー保存則を考える

力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。

単振動

単振動に関する問題を解くときに必要な知識について説明をしています。

力積

力学は物理の基礎とも柱とも言えます。しっかり勉強して理解を深めましょう。

二体問題　Ⅰ

互いに力を及ぼし合う二つの物体の動きを考えます。