この章では、「1.ファラデーの電磁誘導の法則」で電磁誘導について復習し,「Ⅱ.自己インダクタンス」で自己インダクタンスについて考えます。
それらを理解した上で,「Ⅲ.回路の方程式」でコイルを含む回路について,キルヒホッフの法則を適用し,「Ⅳ.直流電源を含む回路の解析」と「Ⅴ.交流電源を含む回路の解析」でそれらの回路について考察します。
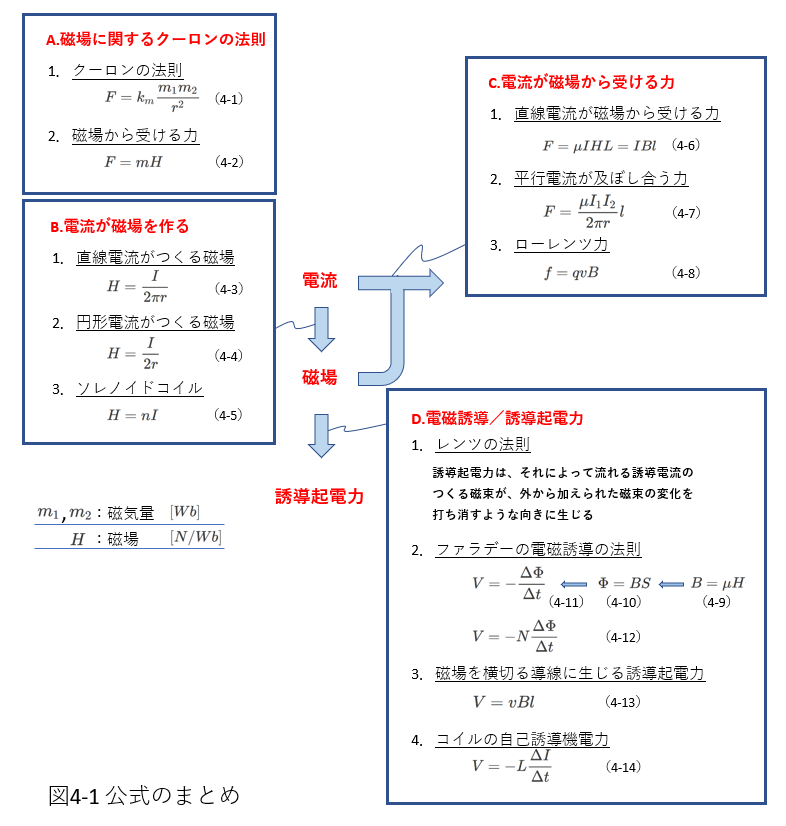
最初に,「電磁気公式」の記事で掲げた図を使って、この記事の範囲を明確にします。
ここでは、下図4-1 「公式のまとめ」の「D.電磁誘導/誘導起電力」を扱います。
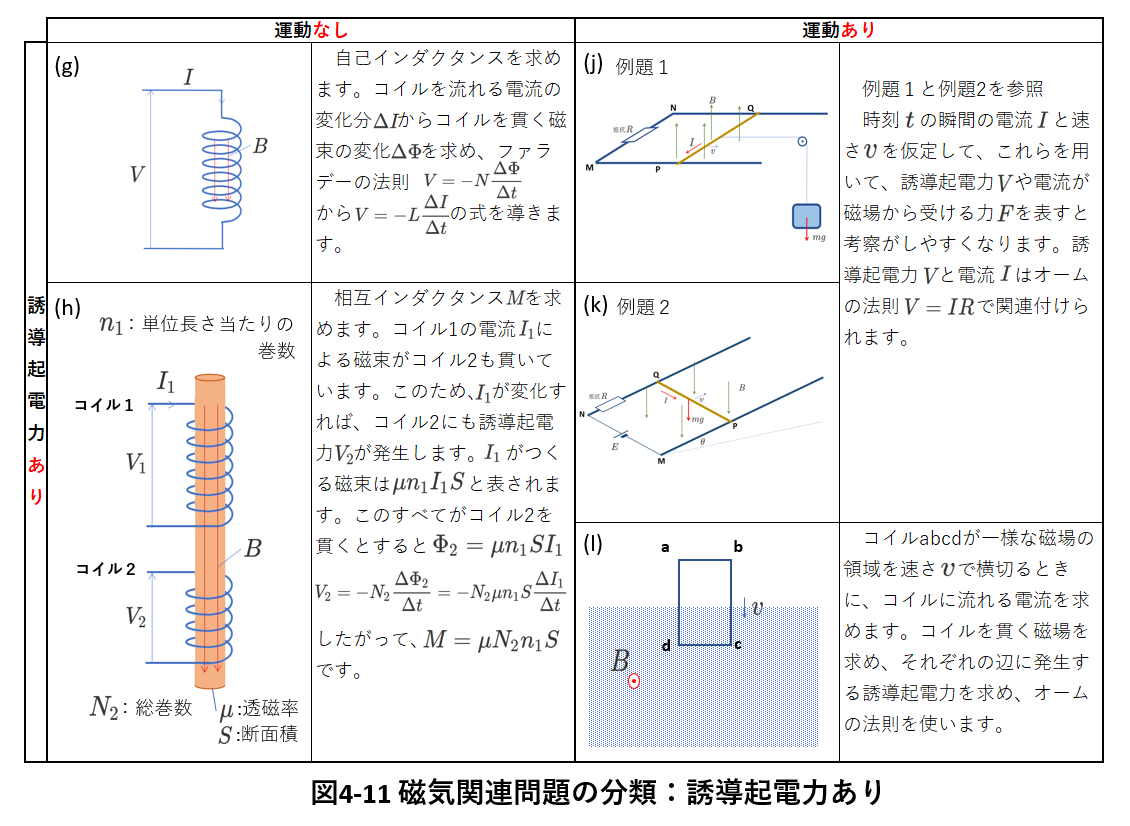
そして、扱う問題の種類としては、下図4-11 「磁気関連問題の分類:誘導起電力あり、かつ、運動なし」です。
Ⅰ.ファラデーの電磁誘導の法則
コイルの内部の磁束の変化によってコイルに電圧が生じる現象が電磁誘導で、生じた電圧が誘導起電力です。
また、このとき流れる電流が誘導電流です。
Ⅰ.レンツの法則とファラデーの電磁誘導の式
誘導電流の向きを考えるには、レンツの法則を使うのが最も分かりやすいです。
レンツの法則:
誘導起電力は、それによって流れる誘導電流のつくる磁束が、
外から加えられた磁束の変化を打ち消すような向きに生じる。
このレンツの法則は、誘導起電力の向きを教えてくれますが、(打ち消すための)磁束を作るのに電流(誘導電流)を流すので、レンツの法則は誘導電流の向きを教えてくれると考えたほうが分かりやすいです。
レンツの法則が示す向きに誘導電流が流れるように誘導起電力が発生すると考えます。
このため、閉回路の一部では、誘導電流は電位の低い側から、高い側に流れる場合があります。
さて、誘導起電力の大きさを計算するには、ファラデーの電磁誘導の式を用います。
ファラデーの電磁誘導の式は、
\begin{equation} V=-N\frac{\Delta \Phi}{\Delta t} \tag{1-1} \label{coil1-1} \end{equation}
です。
ここで、\(V\)は誘導起電力、\(\Delta \Phi\)は時間\(\Delta t\)の間にコイルを貫く磁束の変化、\(N\)はコイルの巻き数、です。
(\ref{coil1-1})式について、次の2点を確認しておきます。
①磁束が変化しない(磁束が一定)の場合、\(\Delta \Phi=0\)ですから、誘導起電力は\(0\)です。
変化しない一定の強さの磁束がコイルを貫いているだけでは誘導起電力は生じないことに注意しましょう。
②磁束の変化が大きい(磁束が急激に変化する)場合ほど、誘導起電力は大きいです。
(\ref{coil1-1})式の負号は、「磁束の変化を打ち消す向きに誘導電流が流れる」、というレンツの法則を表しているのですが、
(\ref{coil1-1})式から誘導電流の向きを知るためには、誘導起電力の正の向きをはっきり知っておく必要があります。
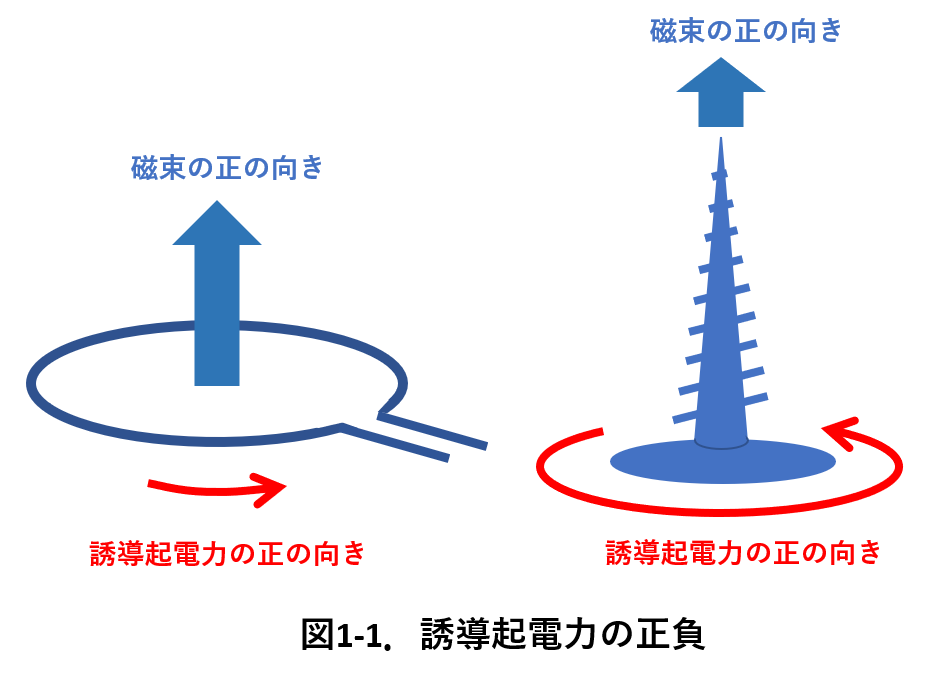
右の図は、磁束の正の向きと誘導起電力の正の向きの関係を示しています。
つまり、誘導起電力の正の向きは、磁束の正の向きに対して決められます。
磁束の正の向きを決めれば誘導機電力の正の向きが決まります。誘導起電力の正の向きを決めれば磁束の正の向きが決まります。
どちらか一方の向きは自由に決められますから,考察をしやすいように決めるのが良いです。
図1-1の右側の図は、それぞれの正の向きの関係を覚えやすくする方法を示しています。
右ねじを回すとき,ねじを回す向きが誘導起電力の正の向き,ねじが進む向きが磁束の正の向きです。
この方法は、右ねじの法則と呼ばれています。
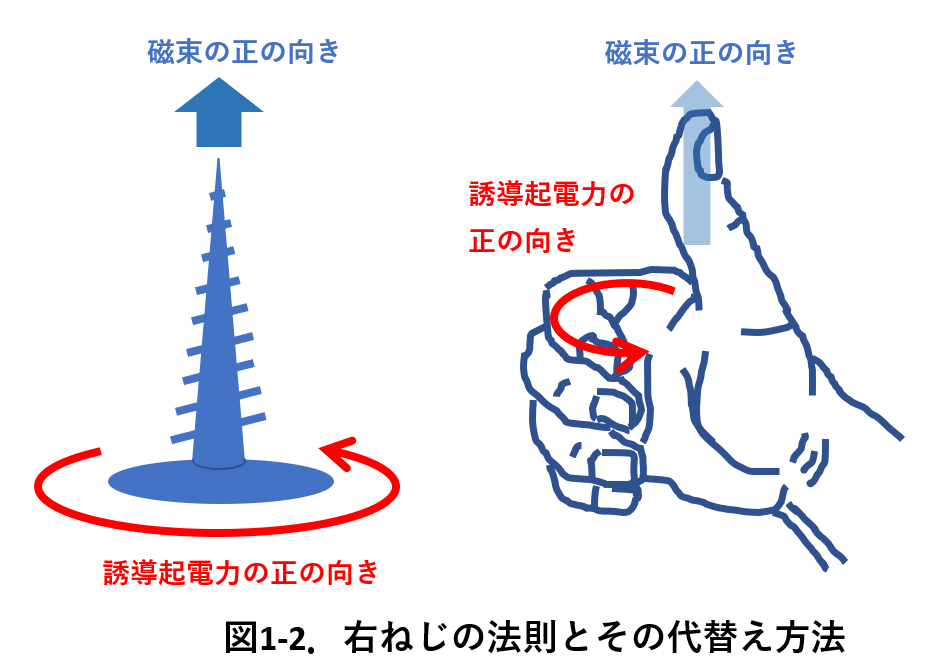
右ねじの法則では考えにくいという人は、図1-2の右側の図に示す方法を試してみてください。
右手の親指を立てて、ほかの4本の指を軽く曲げます。(左手では駄目です。)
立てた親指の示す向きが、磁束の正の向きです。
4本の指は円弧のように見えます。 この円弧を手のひら側から指先に回る向きが誘導起電力の正の向きになります。
どちらの方法でも良いので、覚えやすい方法で、確実に覚えておきましょう。
2.ファラデーの電磁誘導の式から誘導起電力の向きを考える
それでは、ファラデーの電磁誘導の式 (\ref{coil1-1})式と(図1-1)から求まる誘導起電力の向きと、レンツの法則を使って求まる誘導起電力の向きが一致することを確認します。
最初に,ある向きを磁束の正の向きに決めて,2つの方法で求めた誘導起電力の向きが一致することを確認し,
次に,磁束の正の向きを変えても,ファラデーの式で誘導起電力が同じ向きに求まることを確認します。
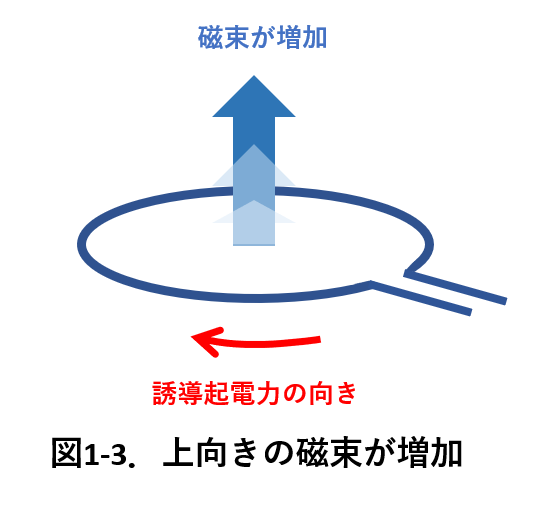
第一の例として、図1-3を考えます。
今コイルを貫通する磁束が上向きで、時間と共に磁束が増加する場合を考えます。
最初に、式(\ref{coil1-1})と図1-1の正の向きから誘導起電力の向きを考えます。まず,磁束の正の向きを上向きと仮定します。すると,誘導起電力の正の向きは図1-1のようになります。
上の条件では,時間\(\Delta t\)に磁束が\(\Phi\)から(\(\Phi+\Delta \Phi\))に変化したと考えると,\(\Phi>0\),\(\Delta \Phi>0\)です。
以上のことから,ファラデーの電磁誘導の式は、
\begin{eqnarray} V=-N\frac{\Delta \Phi}{\Delta t} \\
\frac{\Delta \Phi}{\Delta t} \gt 0 \\
\\
したがって、 V\lt 0
\end{eqnarray}
つまり、誘導起電力は負の向きに生じることがわかりました。
この場合の誘導起電力の向き(負の向き)は図1-3の赤い矢印のようになります。
(赤い矢印が誘導起電力の向きを示していますが、赤い矢印は誘導電流が流れる向きを示していると考えても良いです。)
では、レンツの法則ではどうでしょうか?
レンツの法則によれば、磁束は上向きに増加しています。この増加を妨げるには、下向きに磁束が発生するように誘電電流が流れればよいわけです。
誘導起電力(誘導電流)の向きは,図1-3の赤矢印の向きになり、ファラデーの法則から求めた向きと一致することが確認できました。
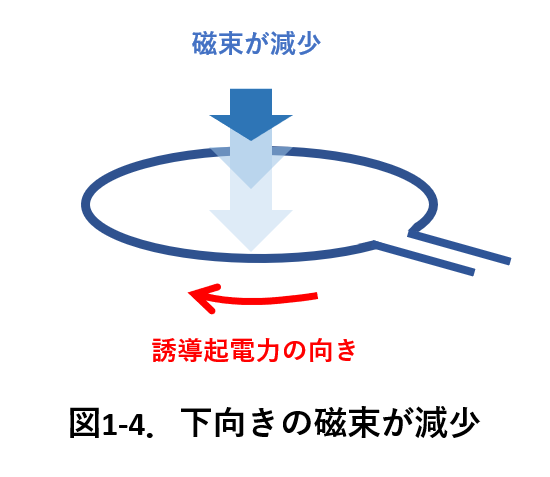
次の第二の例を考えてみましょう。
右の図1-4のように、磁束が下向きで、時間と共に磁束が減少する場合の誘導起電力の向きを考えます。
レンツの法則によれば、磁束は下向きで減少しています。この減少を妨げるには、下向きに磁場が発生するように誘電電流を流せばよいわけです。
つまり、図1-4の赤矢印の向きになります。
次に、ファラデーの電磁誘導の式(\ref{coil1-1})から誘導起電力の向きを考えます。
ここでも磁束の正の向きを上向きにします。すると図1-1から誘導起電力の正の向きが決まります。
これを元に,条件を書き改めて,\(\Delta t\)の間に\(\Phi\)から
(\(\Phi+\Delta \Phi\))に変化したと考えると,\(\Phi<0\),\(\Delta \Phi>0\)です。
\begin{eqnarray} V=-N\frac{\Delta \Phi}{\Delta t} \\
\frac{\Delta \Phi}{\Delta t} \gt 0 \\
\\
したがって、 V\lt 0
\end{eqnarray}
誘導起電力は負の向きに生じます。
上向き正の磁束に対して、負の誘導起電力は図1-4の向きになります。
それでは、今の例において,下向きを磁束の正の向きとして同じ結果が出るかを確認します。
磁束の正の向きを下向きに仮定すると,\(\Phi>0\),\(\Delta \Phi<0\)と考えることになりますから,
\begin{eqnarray} V=-N\frac{\Delta \Phi}{\Delta t} \\
\frac{\Delta \Phi}{\Delta t} \lt 0 \\
\\
したがって、 V\gt 0
\end{eqnarray}
つまり、誘導起電力は正の向きに生じます。 磁束が下向きが正で,誘導起電力が正ということは,図1-4の赤矢印と同じということですから,
正の磁束の向きを上下どちらに仮定しても,誘導機縁力の向きは同じに求められることがわかりました。
図1-4の場合にも、ファラデーの法則とレンツの法則が導く誘導起電力の向きが一致しました。
以上,長く説明しましたが,ファラデーの法則は負号もつけて覚えます。ただし,誘導起電力の向きはレンツの法則から求め,その大きさはファラデーの電磁誘導の式から求めるのがわかりやすく,ミスも少なくなります。
Ⅱ.自己インダクタンス
次に,自己インダクタンスについて考えます。
1.インダクタンス
インダクタンスには自己インダクタンスと相互インダクタンスがあります。相互インダクタンスについては別の章で説明します。
「Ⅰ.ファラデーの電磁誘導の法則」では、コイルに生じる誘導起電力を磁束の変化から求めました。
そして,自己インダクタンスの考えを導入すると,誘導起電力は、コイルの電流の変化から求めることができます。
コイルを含む回路を解析するということは,電流と電圧の関係について考察することですから,自己インダクタンスを用いる方が便利なわけです。
コイルに電流を流せばコイルを貫通する磁束が発生し、電流が変化すればコイルを貫通する磁束も変化しますから、誘導起電力が発生することは,これまでの説明から理解できます。
そして,ソレノイドコイルを貫く磁場の強さは次のように表されます。
\begin{equation}
H=nI
\end{equation}
ここで\(n\)は,単位長さ当たりのコイルの巻き数です。
この式から,磁束の変化量\(\Delta \Phi\)は電流の変化量\(\Delta I\)に比例することがわかります。
比例定数を\(k\)として,
\begin{equation} \Delta \Phi=k\Delta I \end{equation}
これを,ファラデーの電磁誘導の式に代入すれば,コイルの誘導起電力と電流の関係が得られて,
\begin{equation} V=-N\frac{\Delta \Phi}{\Delta t}
=-Nk\frac{\Delta I}{\Delta t}=-L\frac{\Delta I}{\Delta t} \tag{2-1} \label{coil2-1} \end{equation}
\(L\)は上式の比例定数で,コイルの自己誘導起電力の生じやすさを表していて,自己インダクタンスといいます。
この式の負号は,「コイルの誘導起電力は電流の変化を妨げる向きに発生する」ことを示しています。
この説明は後ほどします。
コイルの形状から自己インダクタンスの値を求めることができます。
導出過程は教科書にも載っていて,それが試験にそのまま出題されることもあるので,導出過程の流れを理解しておきましょう。
ファラデーの電磁誘導の式が基本になりますから,\(\Delta \Phi\)を\(\Delta I\)で表すことがポイントです。
透磁率を\(\mu\),コイルの長さを\(l\),コイルの断面積を\(S\)として,
強さ\(I\)の電流が流れているソレノイドの内部の磁束密度は,
\begin{equation} B=\mu H=\mu nI \end{equation}
したがって,ソレノイドを貫く磁束\(\Phi\)は,
\begin{equation} \Phi=BS=\mu nI×S=\mu nSI \end{equation}
コイルの巻き数は\(N=nl\)なので
\begin{equation} V=-N\frac{\Delta \Phi}{\Delta t}=-nl\frac{\mu nS \Delta I}{\Delta t}=-\mu n^2 lS\frac{\Delta I}{\Delta t} \\
故に, L=\mu n^2 lS \end{equation}
次に,上式の負号について考えます。
2.自己インダクタンスの負号について
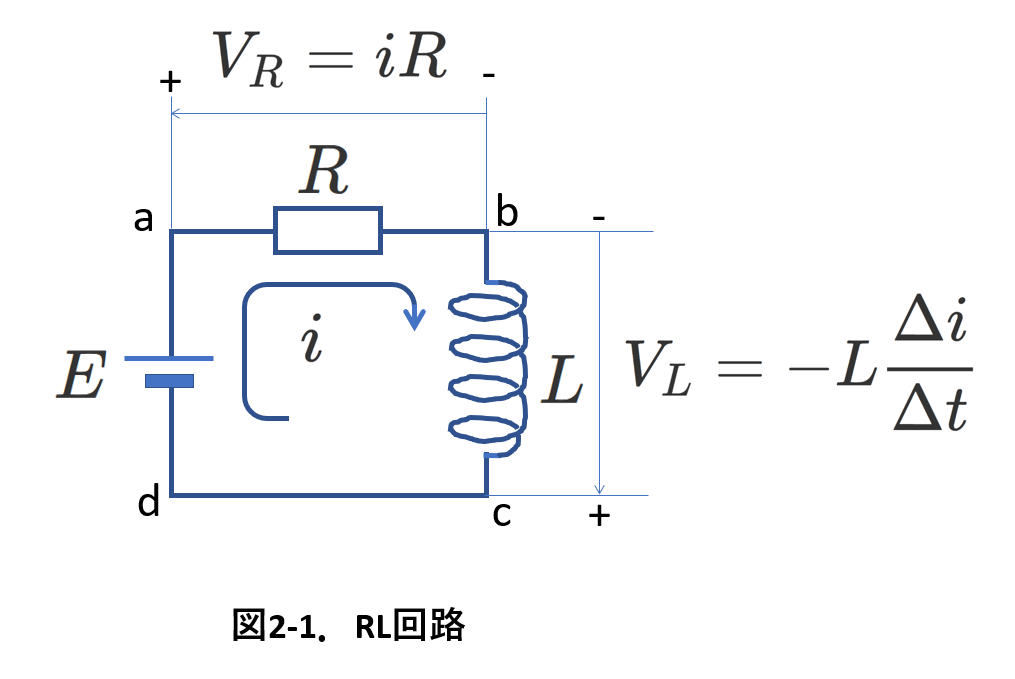
右図2-1の回路で検討してみましょう。
起電力\(E\)の電池と抵抗値\(R\)の抵抗とインダクタンスが\(L\)のコイルが直列に接続されています。
今、図に示した向きに電流\(i\)が流れていると仮定します。電流の向きは勝手に決めて構いません。\(E\)が流す電流の向きと同じに考えた方が考えやすいので,まずこの向きで考えます。
そうして,この仮定した電流の向きに,コイルがコイル以外の回路部分に電流を流そうとする向き(c→d→a→b)が,誘導起電力の正の向きとなります。
(ファラデーの法則で磁束と誘導起電力の正の向きを定義したように,ここでは,電流と誘導起電力の正の向きをこのように定義します。)
このとき、コイルには式(\ref{coil2-1})の誘導起電力が生じます。
誘導起電力は負の負号を持つことから逆起電力と呼ばれることもあります。
キルヒホッフの第2法則を使って、この回路の方程式を立てます。
キルヒホッフの第2法則とは、
回路中のある閉じた経路に注目すると、[起電力の和]=[電圧降下の和]
が、成り立つというものです。
コイルによる誘導起電力(逆起電力)を\(V_L\)とします。
上の式に当てはめれば、
\begin{equation} E+V_L=iR \tag{2-2} \label{coil2-2} \end{equation}
誘導起電力は
\begin{equation} V_L=-L\frac{\Delta i}{\Delta t} \end{equation}
なので,
\begin{equation} E-L\frac{\Delta i}{\Delta t}=iR \tag{2-3} \label{coil2-3} \end{equation}
図には、\(V_R\)と\(V_L\)の両側の電位の高低をしめしました。
\(V_R\)は、点aの方が点bよりも電位が高いです。
\(V_L\)については,(\ref{coil2-1})式で誘導起電力を考えた場合,「\(V_L\)は、点cの方が点bよりも電位が高い」と考えていることになるということです。実際は電流の変化に応じて点bのほうが点cよりも高いといいう場合も生じます。
最初のほうで「コイルの誘導起電力は電流の変化を妨げる向きに発生する」と述べました。
その考えから導き出される誘導機電力の向きと(\ref{coil2-1})式から得られる向きが一致することを確かめられれば,このことがよく理解できるので,ここで確認しておきます。
今、図2-1において、電流\(i\)が増加していくとします。
図のコイルの巻きの向きからすれば、これはコイルの中を上から下に向かう磁束が増えます。
レンツの法則によれば、この磁束の増加を妨げる方向に磁束を生じさせるように誘導電流が流れることになるので、その向きは \(i\) とは逆向きになります。
これは、電位は点cよりも点bの方が高いということです。
ここも分かりにくいことですが、電位を上のように考えると、コイルの中の誘導電流分は電位の低い方から高い方に流れることになります。
電池でも同じことが言えます。
さて,これでは,電流の状態のある特殊な場合についてのみ確認したに過ぎません。
電流の流れる向きが2つ,電流が増加するか減少するかでさらに2つあるので,全部で4つの場合があることになります。
上で検討したものも含め,4つの場合について,「コイルの誘導起電力は電流の変化を妨げる向きに発生する」から導かれる誘導起電力の向きと,自己インダクタンスの(\ref{coil2-1})式から求められる誘導起電力の向きが一致することを次の表に表します。
| 場合分け | 電流の変化を妨げる向き | 自己インダクタンスの式から |
|---|---|---|
|
時刻\(\Delta t\)の間に電流が\(I\)から\(I+\Delta I\)に変化するとして, |
Iが正の向きに増加するので,それを妨げるため負の向きに誘導起電力が発生する | \(V=-L\frac{\Delta I}{\Delta t}<0\) |
| \(I>0\),\(\Delta I<0\) の場合 | 正の向きに流れている\(I\)が減少するので,それを妨げるため正の向きに誘導起電力が発生する | \(V=-L\frac{\Delta I}{\Delta t}>0\) |
|
\(I<0\),\(\Delta I>0\) の場合 |
負の向きに流れている\(I\)の強さが減少するので,それを妨げるため負の向きに誘導起電力が発生する | \(V=-L\frac{\Delta I}{\Delta t}<0\) |
|
\(I<0\),\(\Delta I<0\) の場合 |
負の向きに流れている\(I\)の強さが増加するので,それを妨げるため正の向きに誘導起電力が発生する | \(V=-L\frac{\Delta I}{\Delta t}>0\) |
起こりうる4つの場合について,2つの方法で求めた向きが一致することが確認できました。
負号が向きを決定する上で重要な意味を持っていることがわかります。
回路を解析するとき,電流の流れの向きを自分の好きなように(解きやすいように)決めて良いと述べました。
これが正しいことを説明するため,上の例で電流の向きを逆に仮定して回路の方程式を立ててみましょう。
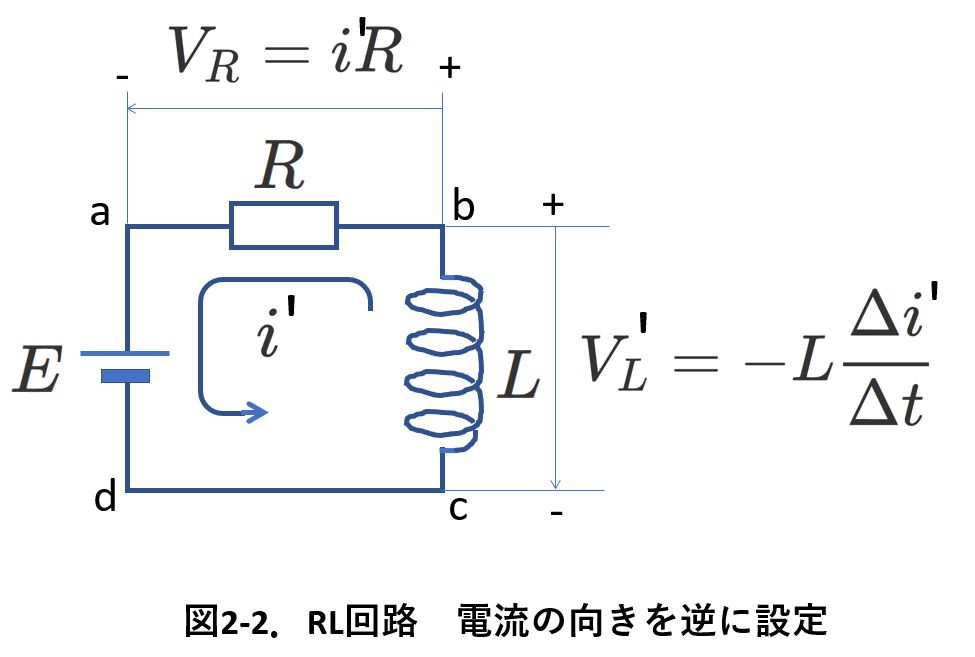
すると、図2-2のようになります。
電流の向きが逆になったので、\(R\)と\(L\)への電圧の正負が逆になっていることに注意してください。
さて、この回路の起電力は、\(E\)と\(V'_L\)ですが、\(i\) を図の向きに流すには、電池の起電力は負でないといけないので、Eを起電力の大きさとして,
\begin{equation} -E+V'_L=i'R \tag{2-4} \label{coil2-4} \end{equation}
式(2-2)と式(2-4)は違っているように見えますが、これは電流の向きを逆向きにしたためです。
その向きを考えた場合、\(i'=-i、V'_L=-V_L\)ですから、これらの式を(2-4)に代入すると、
\begin{eqnarray} -E+(-V_L)=(-i)R \\
E+V_L=iR \end{eqnarray}
このように、式(2-2)と等価であることが証明できました。
先ほどの式は,\(i\)の正負に関係なく,同じ式で表されると分かります。
同時に,最初の例のように,電池の起電力が流す電流の向きに,電流の正の向きを設定するのがわかりやすいと理解できます。
3.合成インダクタンス
ここでは,2個のコイルを直列につないだ場合と並列につないだ場合の合成インダクタンスがいくつになるかを調べます。
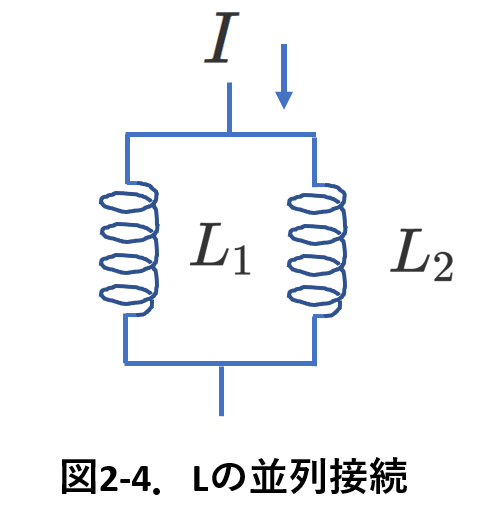
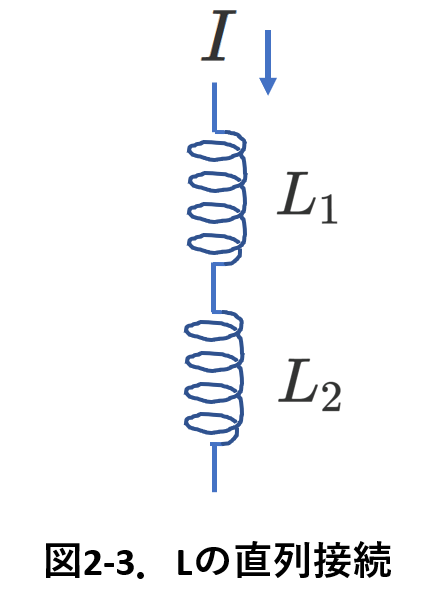
接続した図を,図2-3(直列の場合)と図2-4(並列の場合)に示しました。
このときの重要なポイントは,一方のコイルが作る磁束がもう一方のコイルを貫くことがないほど離れていると仮定する必要があることです。
仮に,一方のコイルが作る磁束の一部分でも,もう一方のコイルを貫くということになると,その磁束が変化すれば,もう一方のコイルに(相互)誘導起電力が発生しますから,相互インダクタンスを考慮しなければなりません。
ここでは,それを考慮しなくてもすむようにふたつのコイルが配置されているとして,合成自己インダクタンスがいくつになるかを考えます。
合成インダクタンスを求めるにはどう考えればいいかを図-2-5に示します。
自己インダクタンスが\(L_1\)と\(L_2\)のふたつのコイルが直接に繋がっています。
ここに電流\(I\)が流れて,ふたつのコイルの作る誘導起電力を\(V_L=-L\frac{\Delta I}{\Delta t}\)と表したとき,\(L\)は\(L_1\)と\(L_2\)を使ってどのように表されるかを考えます。
つまり,\(L_1\),\(L_2\)の誘導起電力から接続方法に合わせて計算し,\(V_L=-L\frac{\Delta I}{\Delta t}\)の形に変形します。
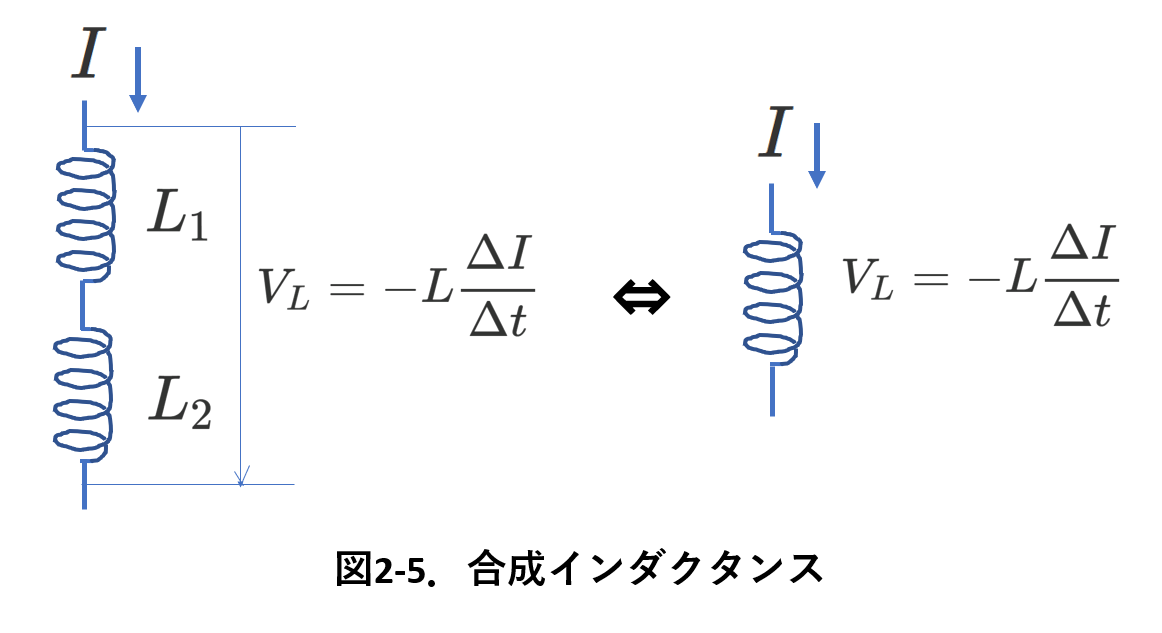
図2-3の直列接続ではふたつのコイルに流れる電流は同じです。
\(L_1\)の電圧は,\(-L_1\frac{\Delta I}{\Delta t}\)
\(L_2\)の電圧は,\(-L_2\frac{\Delta I}{\Delta t}\)
したがって,ふたつのコイルの電圧の和\(V_L\)は,
\begin{eqnarray}
V_L&=&-L_1\frac{\Delta I}{\Delta t}-L_2\frac{\Delta I}{\Delta t} \\
&=&-(L_1+L_2)\frac{\Delta I}{\Delta t} \\
これより, L=L_1+L_2
\end{eqnarray}
次に図2-4の並列接続について考えます。
この場合,ふたつのコイルの誘導起電力は同じでなければなりません。
そしてこの誘導起電力がふたつのコイルを並列に配置した時の誘導起電力そのものです。
そして,コイル\(L_1\)を流れる電流を\(I_1\),コイル\(L_2\)を流れる電流を\(I_2\)とすると,\(I=I_1+I_2\)です。
以上2つの内容を式に表すと,
\begin{eqnarray}
I&=&I_1+I_2 \\
-L_1\frac{\Delta I_1}{\Delta t}&=&-L_2\frac{\Delta I_2}{\Delta t}
\end{eqnarray}
第1式から\(I_2\)を求め,第2式に代入します。
\begin{eqnarray}
-L_1\frac{\Delta I_1}{\Delta t}&=&-L_2\frac{\Delta (I-I_1)}{\Delta t} \\
-L_1\frac{\Delta I_1}{\Delta t}&=&-L_2\frac{\Delta I}{\Delta t}+L_2\frac{\Delta I_1}{\Delta t} \\
-(L_1+L_2)\frac{\Delta I_1}{\Delta t}&=&-L_2\frac{\Delta I}{\Delta t}
\end{eqnarray}
ところで,
\begin{eqnarray}
V_L&=&-L_1\frac{\Delta I_1}{\Delta t}=-L_1×\frac{L_2}{L_1+L_2}\frac{\Delta I}{\Delta t} \\
したがって,L&=&\frac{L_1L_2}{L_1+L_2}
\end{eqnarray}
Ⅲ.回路の方程式
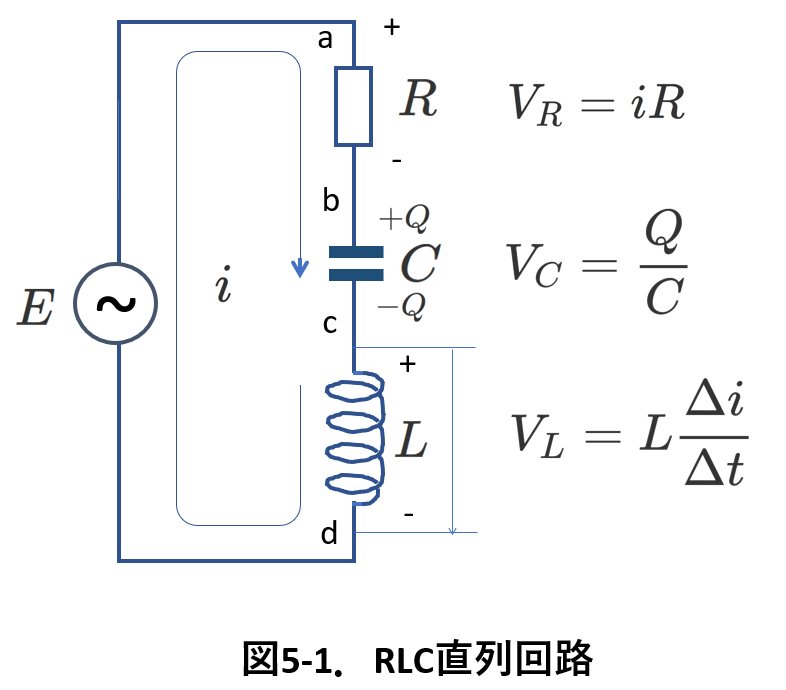
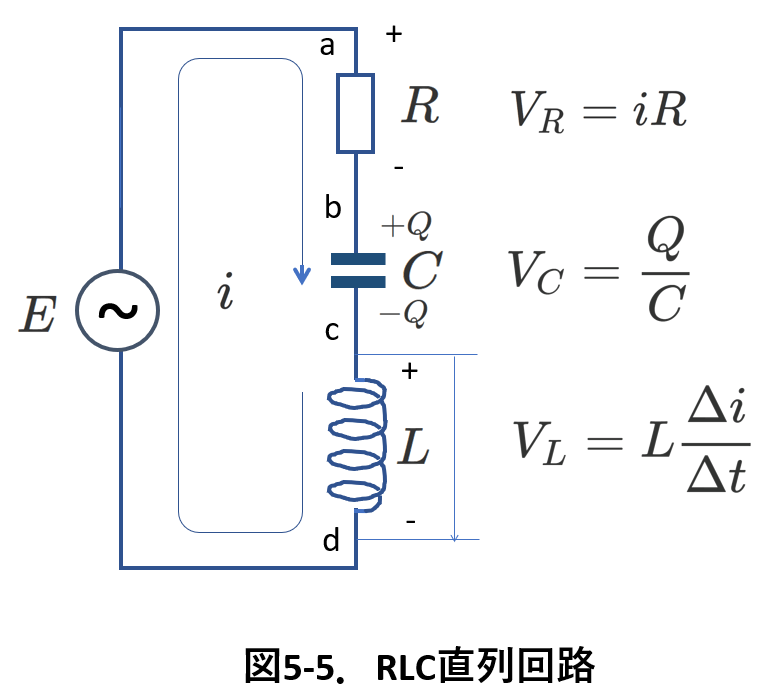
この章では,RLC直列回路について,その方程式(電圧に関する式)を求めます。
最初に,抵抗値Rの抵抗と電気容量Cのコンデンサと自己インダクタンスLのコイルが,起電力Eの直流電源に対して直列に接続された回路を考えます。
これを図3-1 に示します。
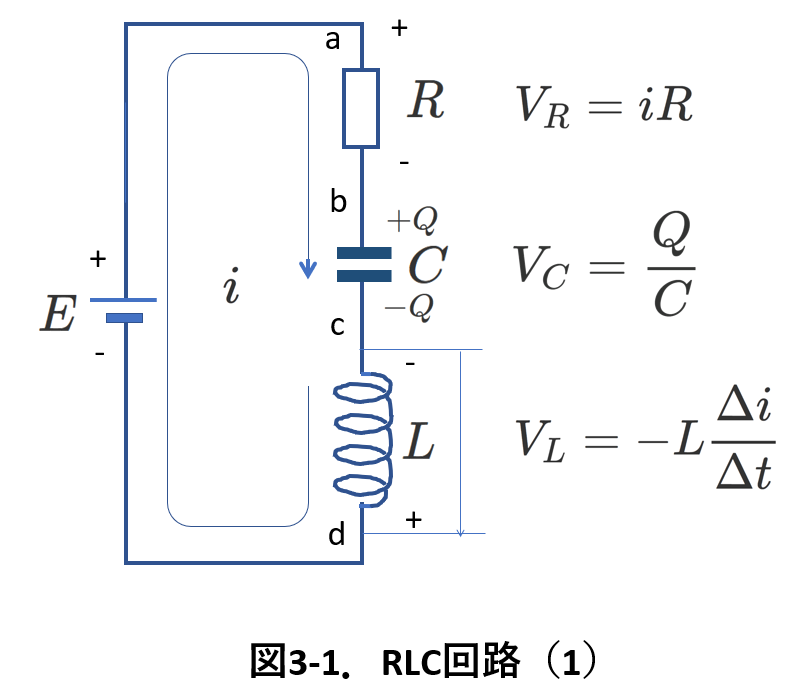
そして,最初に,回路に流れる電流\(i\)の向きを仮定します。直流電源の向きに合わせて図3-1のように仮定します。
また,コンデンサーに蓄えられている電荷を\(Q\)とします。
コンデンサーの2枚の極板にはそれぞれ\(+Q\)と\(-Q\)が存在することになります。
回路の方程式を立てたり,考察するときには,どちらの極板に+-どちらの電荷が溜まっているかを図に示した方がミスが少なくなります。
そして,この回路においては,電流が流れ込む側の極板が\(+Q\)で,流れ出る側の極板が\(-Q\)です。
さて,キルヒホッフの第2法則は,回路中のある閉じた経路(図3-1ではこれはひとつしかありません)に注目すると,
[起電力の和]=[電圧降下の和]です。
図3-1にはそれぞれの部品について,その両端のどちらを+-と考えているかを示してあります。また,そのときのR,L,C各部品の電圧を表す式も添えました。
特に,コイル両端の電圧の向きが抵抗やコンデンサーと逆であること,\(V_L\)には負号がついていることに注意しましょう。これは,Ⅱ.「2.自己インダクタンスの負号について」で説明しました。
それを用いて,キルヒホッフの第2法則にそのまま入れれば,
\begin{equation} E+(-L\frac{\Delta i}{\Delta t})=Ri+\frac{Q}{C} \tag{3-1} \label{coil3-1} \end{equation}
となります。
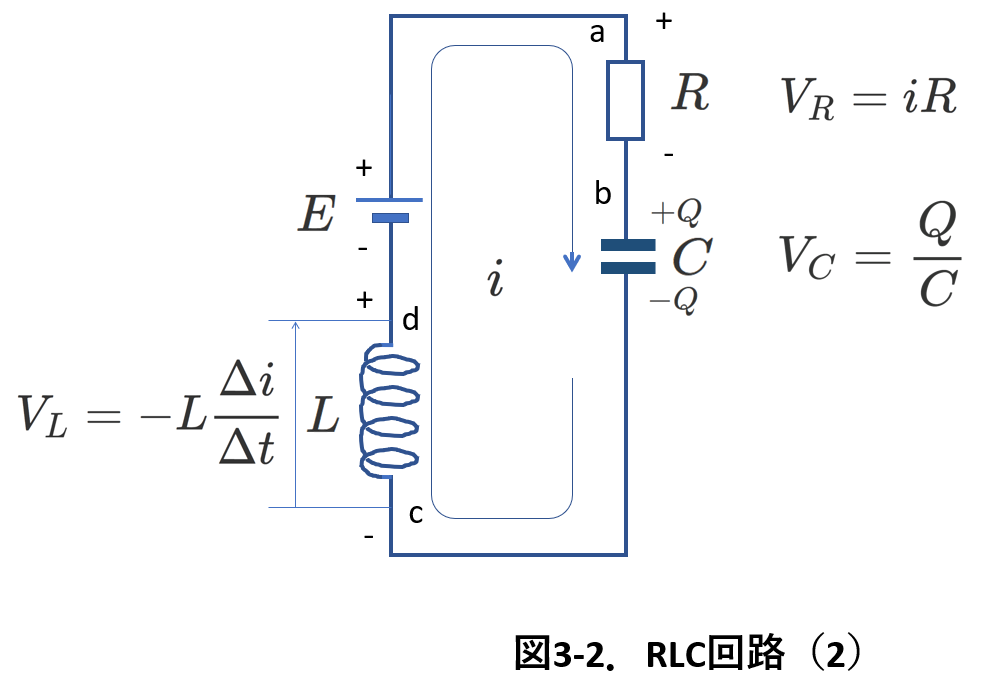
図3-2は,この式を図に表す目的で,図3-1を起電力側と電圧降下側に分けて描いたものです。
コイルの誘導起電力の正の向きが電源の起電力の正の向きと同じになっていることに注意しましょう。
ところで,
\begin{equation} i=\frac{\Delta Q}{\Delta t} \tag{3-2} \label{coil3-2} \end{equation}
です。
これは,電流が,単位時間に通過する電気量(電荷)として定義されていることからわかります。
つまり,時間 \(\Delta t\) の間に流入した電荷 \(i\Delta t\) がコンデンサーの極板の電荷の増加量\(\Delta Q\)に等しいので,\(i\Delta t=\Delta Q\)から上の(\ref{coil3-2})式が導かれます。
この式を(\ref{coil3-1})式に代入すると,次のようになります。
以下の式では,\(\Delta\)を用いるのをやめて,微分形式で表現しています。
\begin{equation} E+(-L\frac{di}{dt})=Ri+\frac{Q}{C} \\
E=Ri+\frac{Q}{C}+L\frac{di}{dt} \end{equation}
\begin{equation}
E=L\frac{d^2Q}{dt^2}+R\frac{dQ}{dt}+\frac{Q}{C} \tag{3-3} \label{coil3-3}
\end{equation}
結局,\(Q\)についての2階の微分方程式になりました。
この方程式を解くのは難しいので,特別な場合を除いて,この微分方程式を解くことはありません。
さて,(\ref{coil3-1})式は,次のようにも書き換えられます。
\begin{equation} E=Ri+\frac{Q}{C}+L\frac{\Delta i}{\Delta t} \tag{3-4} \label{coil3-4} \end{equation}
この式は図3-1の回路に於いて,キルヒホッフの第二法則に関わる起電力側は直流電源だけで,電圧降下側は抵抗,コンデンサー,コイルの3つであると考えることができることを示しています。
このときの回路図を,図3-3に示しました。,
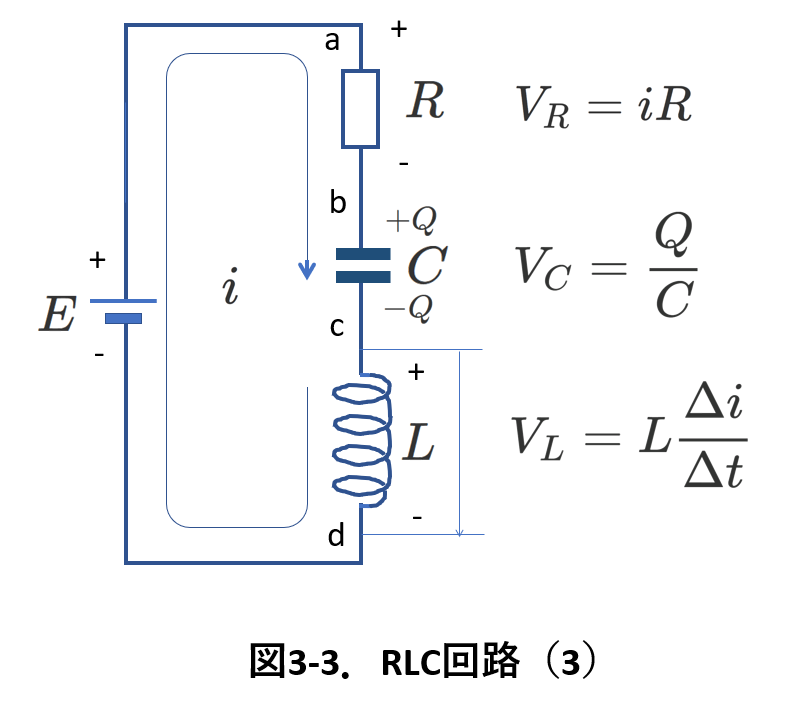
コイルの電圧降下を考える場合,+-は抵抗やコンデンサーと同じ向きで,電圧降下は\(+L\frac{\Delta i}{\Delta t}\) と考えれば良いことがわかります。
コイルを逆起電力として扱うか,電圧降下素子として扱うかは,どちらがわかりやすいと考えるかに依ります。
ただ,どちらも知っていた方が符号ミスが減らせるのではないかと思います。
そして,電源が交流の場合には,電圧降下素子として扱います。
Ⅳ. 直流電源を含む回路の解析
ここでは,コイルを含む回路がどのように働くかを考察します。
最初に注意するのは,電源が直流なのか,交流なのかです。
電源がどちらであっても回路の方程式(つまり,微分方程式)を立てて,解けば正しい解が得られるはずですが,微分方程式の解法は高校レベルでは難しいため,非常に簡単なものを除いて,微分方程式を使って解析する問題は出題されません。
そのため,特別な場合について定性的に解くことが主流になります。
また,直流電源と交流電源を扱う回路では,解析するときの考え方が異なります。
この章では,電源が直流の場合を考えます。
1.RL回路(1)
直流電源でコイルの問題を考える場合,次の考えが基本になります。
コイルは,そこに流れている電流の変化を減らす(妨げる)ようにはたらきます。
したがって,スイッチなどを開閉することで回路の状態が変化しようとするとき
・その直後は,コイルに流れる電流をそのままにしようとします。
つまり,スイッチ開閉直後は,直前の電流が保持されると考えます。
・十分時間が経過した後では,電流は一定となり,定常状態になります。
電流が一定となれば,コイルの電圧は\(0\)になります
以上のことを頭に入れて,次の2つの回路の動作を考えます。
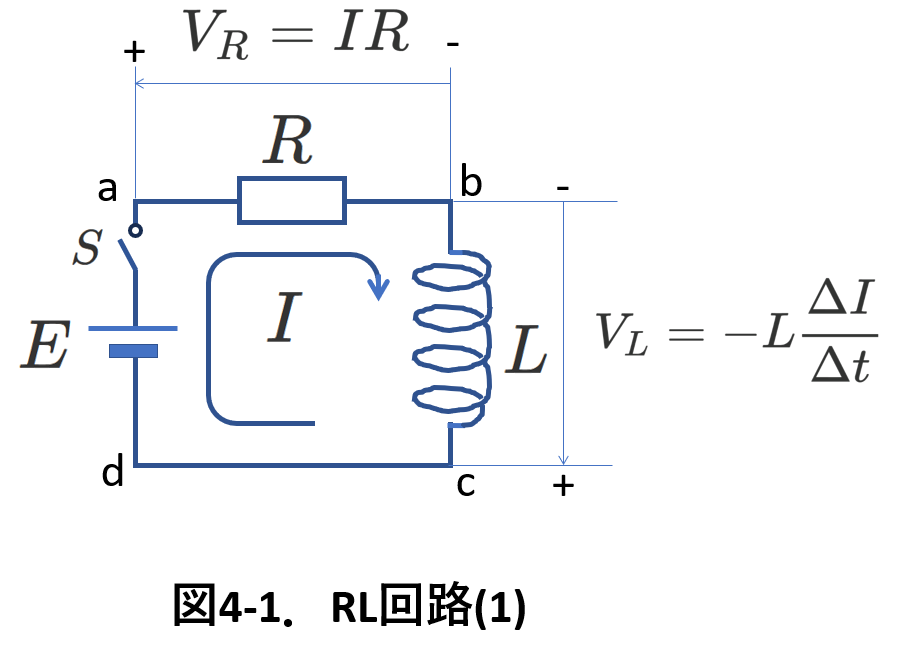
図4-1において,\(t=0\)でスイッチSを閉じたとします。
それ以降のコイルに流れる電流の時間変化のグラフ(I-tグラフ)を描くことを考えます。
Sを閉じる前はコイルを流れる電流は\(0\)ですから,Sを閉じた直後も電流は\(0\)です。
電流が0ならば,コイルの誘導起電力\(V_L\)は\(V_L=-E\)のはずです。
さて,この回路の方程式は,(\ref{coil2-3})式で与えられます。ここでは,この式を(4-1)式として,
\begin{equation} E-L\frac{\Delta I}{\Delta t}=IR \tag{4-1} \label{coil4-1} \end{equation}
これを変形して,
\begin{equation} L\frac{\Delta I}{\Delta t}=E-IR \tag{4-2} \label{coil4-2} \end{equation}
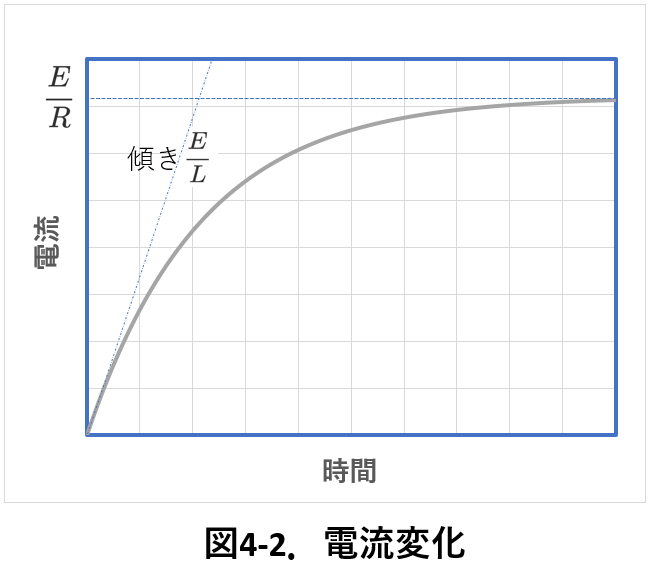
(\ref{coil4-2})式から,\(t=0\)での\(\frac{\Delta I}{\Delta t}\)の値(すなわち,I-t グラフの傾き)が\(\frac{E}{L}\)であるとわかります。
そして,電流は増加していきますから,(\ref{coil4-2})式から,グラフの傾きは時間が経つにつれて小さくなっていきます。
つまり,電流の増加割合は徐々に減少し,最後には一定となることがわかります。
時間が十分に経過した後の電流値は,(\(\ref{coil4-1}\))式で,\(\frac{\Delta I}{\Delta t}=0\)とおいて,\(\frac{E}{R}\)が得られます。
このとき,誘導起電力は,\(V_L=-L\frac{\Delta I}{\Delta t}=0\) です。
コイルに電流が流れていても,コイルの誘導起電力,あるいは,コイルの電圧が\(0\)というのは,少し不思議に思われるかもしれませんが,ファラデーの法則から導かれたものです。
そういう状態があるということを,しっかり理解しておきましょう。
今までの考察から\(I-t\)グラフは図4-2のようになります。
では,ここで微分方程式(\ref{coil4-1})式を解いて図4-2と比較してみましょう。
微分形式に直して,変形します。
\begin{eqnarray} I'&=&I-\frac{E}{R}とおけば,\frac{dI}{dt}=\frac{dI'}{dt} \\
L\frac{dI'}{dt}+RI&=&0 \\
\frac{1}{I'}\frac{dI'}{dt}&=&-\frac{R}{L} \\
\int \frac{1}{I'}dI'&=&-\int \frac{R}{L}dt \\
lnI'&=&-\frac{R}{L}t+C \\
I'&=&e^Ce^{-\frac{R}{L}t} \\
I&=&I'+\frac{E}{R}=e^Ce^{-\frac{R}{L}t}+\frac{E}{R} \\
t=0で I&=&0であることから 0=e^C+\frac{E}{R} \\
e^C&=&-\frac{E}{R} \\
ゆえに,I&=&-\frac{E}{R}e^{-\frac{R}{L}t}+\frac{E}{R}=\frac{E}{R}(1-e^{-\frac{R}{L}}) \tag{4-3} \label{coil4-3}
\end{eqnarray}
(\ref{coil4-3})式が,図4-2と一致することを確認しましょう。
この結果を元にコイルの誘導起電力を計算します。
\begin{equation} V_L=-L\frac{dI}{dt}=-Ee^{-\frac{R}{L}t} \tag{4-4} \label{coil4-4} \end{equation}
この式から,時間\(t=0\)で\(V_L=-E\),時間が十分に経過すると\(V_L=0\)となることがわかります。
前の定性的な考察結果と一致しました。
2.RL回路(2)
次に,図4-3の回路を考察します。
これは,東海大で出題された回路です。
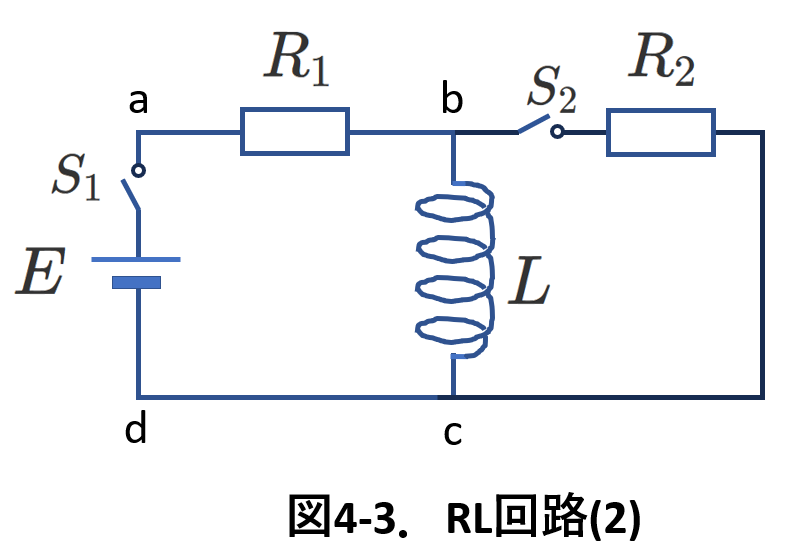
最初に,\(S_2\)を開いた状態で,\(S_1\)を閉じます。
この状態は,図4-1と同じです。
したがって,十分に時間が経てば,コイルの誘導起電力は\(0\)で,電流は一定値の\(\frac{E}{R_1}\)となります。
ここで,\(S_2\)を閉じると,コイルの電圧は\(0\)ですから,抵抗\(R_2\)の電圧も\(0\)で,抵抗\(R_2\)には電流は流れません。
次に,\(S_1\)を開くと,開く直前にはコイルに\(\frac{E}{R_1}\)の電流が流れていて,\(S_1\)を開いた直後はこの電流を維持しようとするので,この電流は\(R_2\)を流れます。電流が流れる向き(c⇒\(R_2\)⇒b⇒c)に注意してください。
コイルにあったエネルギーが抵抗\(R_2\)で消費されて熱に変わるので,電流は次第に減少して,最後には\(0\)になります。
\(S_1\)を開いた時刻を\(0\)として,回路の方程式を立てて解こうとするには,(\ref{coil4-1})式で\(E=0\),\(R\)を\(R_2\)として解くことになります。
ただ初期条件は,\(t=0\)で\(I=\frac{E}{R}\)を与えます。
Ⅴ.交流電源を含む回路の解析
ここでは電源が交流の場合の回路解析を扱います。
1.基本的な考え方
右図5-1のようなRLC直列回路に交流電源が繋がっている場合を考えます。
交流電源の電圧が\(E\sin\omega t\)であるとすると,各素子の電圧,電流も同じ角周波数\(\omega\)で周期的に変化します。
このことは次のように考えると理解できます。
キルヒホッフの法則は交流回路においても,どの瞬間でも成り立ちます。
仮に,各素子の電圧の角周波数が異なるとすると,ある瞬間にキルヒホッフの第2法則が成り立っても,次の瞬間には成立しないことになります。
したがって,交流回路の回路解析をするということは,各電圧,電流を,\(A\sin(\omega t+\theta)\)の形に表す,つまり,最大値\(A\)と位相差\(\theta\)を求めることになります。
ただし,回路にスイッチを入れた直後には,\(A\sin(\omega t+\theta)\)の形にはなりません。
回路からすれば,スイッチを閉じた瞬間,突然電圧をくわえられるのですから,その瞬間は直流電源電圧が加えられたような状態になります。
スイッチを閉じた瞬間から\(A\sin(\omega t+\theta)\)の定常状態に達するまでの電流や電圧の変化を過渡応答と言って,定常状態とは区別して考えます。もちろん,回路の微分方程式を厳密に解けば,過渡応答から定常状態までを解析できるわけですが,これを扱うのは非常に難しいので,出題は定常状態に関するものに限られます。
たいていの場合,1周期ぐらいで,\(A\sin(\omega t+\theta)\)になります。
2.リアクタンスと位相
「1.基本的な考え方」で最大値と位相を知ることが大事という話をしました。
そこで,ここでは,各素子の電流と電圧について最大値と位相の関係を示しておきます。
・コイルに\(I_0\sin\omega t\)の電流が流れたとき,コイルの電圧は\(\omega LI_0 \sin(\omega t+\frac{\pi}{2})\)となります。
・コンデンサーに\(I_0\sin\omega t\)の電流が流れたとき,コンデンサーの電圧は\(\frac{I_0}{\omega C} \sin(\omega t-\frac{\pi}{2})\)となります。
・抵抗に\(I_0\sin\omega t\)の電流が流れたとき,抵抗の電圧は\(RI_0 \sin\omega t\)となります。
コイルの\(\omega L\)とコンデンサーの\(\frac{1}{\omega C}\)は最大値を求めるために抵抗値のような働きをする係数で,リアクタンスと呼ばれます。
では,リアクタンスを理論的に求めてみましょう。
重要なポイントは,交流電源に繋がれたコイルを解析するときには,コイルを電圧降下素子として扱うので,誘導起電力の場合と異なり負号はつけないということです。図5-1で\(V_L\)の式を確認してください。
つまり,次のようになります。
\begin{eqnarray}
コイルの電圧V_Lは, \\
V_L&=&L\frac{d}{dt}I_0\sin \omega t=\omega LI_0\cos\omega t=\omega LI_0\sin(\omega t+\frac{\pi}{2}) \tag{5-1}\label{coil5-1} \\
I&=&\frac{dQ}{dt}=C\frac{dV_C}{dt} より, \\
コンデンサーの電圧V_Cは, \\
V_C&=&\frac{1}{C}\int Idt=\frac{1}{C}I_0\frac{1}{\omega}(-\cos\omega t) \\
&=&\frac{I_0}{\omega C}\sin(\omega t -\frac{\pi}{2}) \tag{5-2}\label{coil5-2}
\end{eqnarray}
位相に着目すると,
・コイルの電圧はコイルを流れる電流よりも位相が\(\frac{\pi}{2}\)だけ進んでいます。
・コンデンサーの電圧は,コンデンサーを流れる電流よりも位相が\(\frac{\pi}{2}\)だけ遅れています。
どちらの位相が進んでいるか,遅れているかは覚えづらいですが,次のようなイメージを持つと覚えやすいと思います。
コイルに電圧をかけてもすぐには電流は流れず,遅れて電流が流れます。
コンデンサーに電圧をかけると,瞬時に電流は流れますが,流れた電流が電荷として蓄積されて遅れて電圧が上昇します。。
3.電圧,電流のベクトル表示
電圧,電流ともに交流回路では\(A\sin(\omega t+ \theta)\)と表されます。つまり,交流電圧や交流電流は最大値と位相差で代表できるので,図5-2に示したようにベクトル表示ができます。
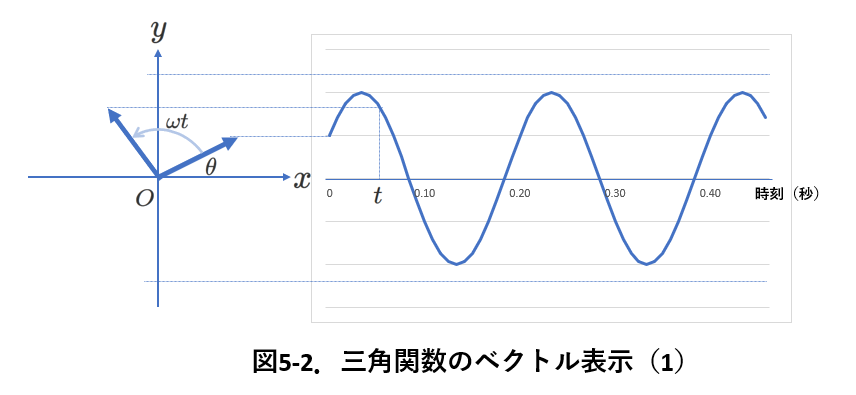
xy平面上に原点Oを中心とした矢印を考えます。この矢印が反時計向きに回転すると考えます。このとき,ベクトルのy方向成分,または,ベクトルのy軸への正射影が\(A\sin(\omega t+\theta)\)を表します。この様子を図5-2の右図に表しています。今ベクトルは\(t=0\)で図の位置(すなわち,位相差が\(\theta\)の位置)にあります。時刻\(t\)ではベクトルは\(\omega t\)だけ回転し,位相は\(\omega t+\theta\)になります。このときのベクトルのy成分が時刻\(t\)の電圧または電流の値になります。
このベクトル表示で,コイルの電流と電圧を表すと,図5-3のようになります。
同じxy平面上に,電圧と電流の両方を表すことが出来ることに注意してください。
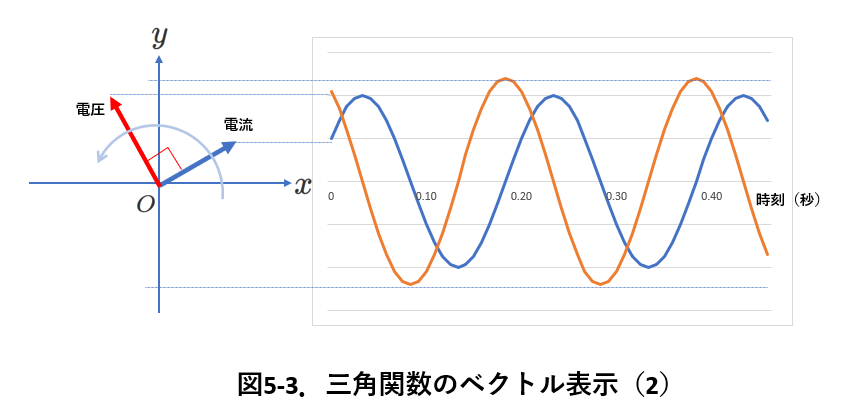
コイルの電圧は電流よりも\(\pi/2\)だけ進んでいるので,図5-3のように表されます。
時間が経つと,電流と電圧のベクトルは位相差\(\pi/2\)を維持したまま反時計の向きに回転するので,そのy成分は時間に対して,図5-3の右側のグラフのように変化します。
ここで,三角関数の公式,
\begin{eqnarray} a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta +\alpha) \tag{5-3}\label{coil5-3} \\
\tan\alpha=\frac{b}{a} \tag{5-4} \label{coil5-4}
\end{eqnarray}
をベクトル表示で確認してみます。
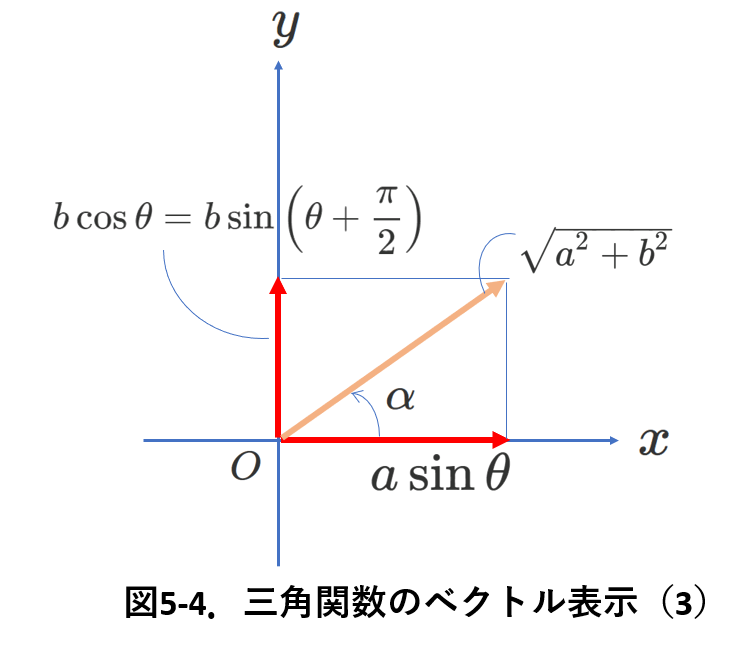
それが図5-4です。
\(b\cos\theta=b\sin(\theta+\pi /2)\)ですから,\(a\sin\theta\)と\(b\cos\theta\)をxy平面に表すと図5-4になります。
\(a\sin\theta\)の矢印の長さは\(a\),\(b\cos\theta\)の長さは\(b\)です。
2つの三角関数の足し算は,ベクトルの足し算となります。
ベクトルの足し算で得られた和は,オレンジ色の矢印で表されています。
この長さ(すなわち,\(a\sin\theta+cos\theta\)の大きさ)は,\(\sqrt{a^2+b^2}\)です。
これは,公式(\ref{coil5-3})式に一致します。
また,\(\tan\alpha\)の値も上の公式(\ref{coil5-4})式の通りであることがわかります。
4.RLC回路
それでは,具体的な回路について,ベクトル表示を用いて解析します。
最初の回路は,図5-5のRLC直列回路です。
4-1.RLC直列回路
この回路に電源から\(i=I_0\sin\omega t\)の電流が流れたときの電源の電圧を求めます。
物理の問題でよく見かける考え方ですが,何が各素子に共通で,何が各素子に個別なのかに注意します。
図5-5の直列回路で言えば,共通な(同じ)ものは各素子を流れる電流です。
この回路で,直流電源の場合と同じように\(i\)の電流の正の向きを考え,それに対して各電圧降下素子の電位の+-を設定していることに注意しましょう。
交流だから,+側だけを考えてはいけないと思うかもしれませんが,立てた式は\(i\)が負の場合にも成立することは前に示した通りです。つまり,電流の+に対して各電圧降下素子の+-を設定しておけば電流が+でも-でもカバーできることになりますから,方程式が立てやすいです。
「2.リアクタンスと位相」で説明したように,コイルの電圧の位相は電流よりも\(\frac{\pi}{2}\)進んでいます。
抵抗の電圧は,電流と同位相です。
コンデンサーの電圧の位相は電流よりも\(\frac{\pi}{2}\)遅れています。
ベクトル図では,ある時刻の位相関係を図示しているので,描きやすい時刻でベクトル図を描くのが楽です。
ここでは設定どうりに,\(i=I_0\sin\omega t\) として,ベクトル図は図5-6のようになります。
すべての素子を流れる電流\(I_0\sin\omega t\)を基準として,3素子の電圧のベクトル図を描いています。
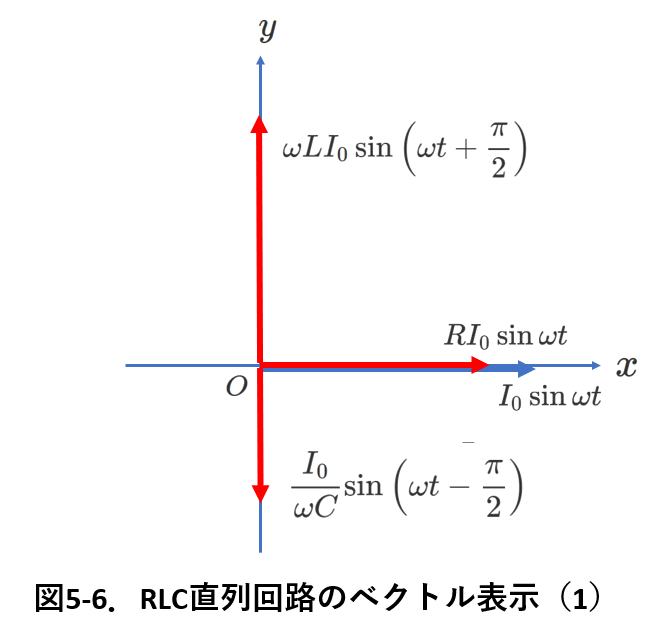
リアクタンスを考慮すれば,
コイルの電圧は,\(\omega LI_0\sin(\omega t+\frac{\pi}{2})\),
抵抗の電圧は,\(RI_0\sin\omega t\),
コンデンサーの電圧は,\(\frac{I_0}{\omega C}\sin(\omega t-\frac{\pi}{2})\)
です。
これを表して,図5-6のようになります。
また\(\sin\)を略して,各電圧の最大値だけで表せば,図5-7となります。この表し方が普通です。
図5-7で,これら3つのベクトルの足し算を考えます。
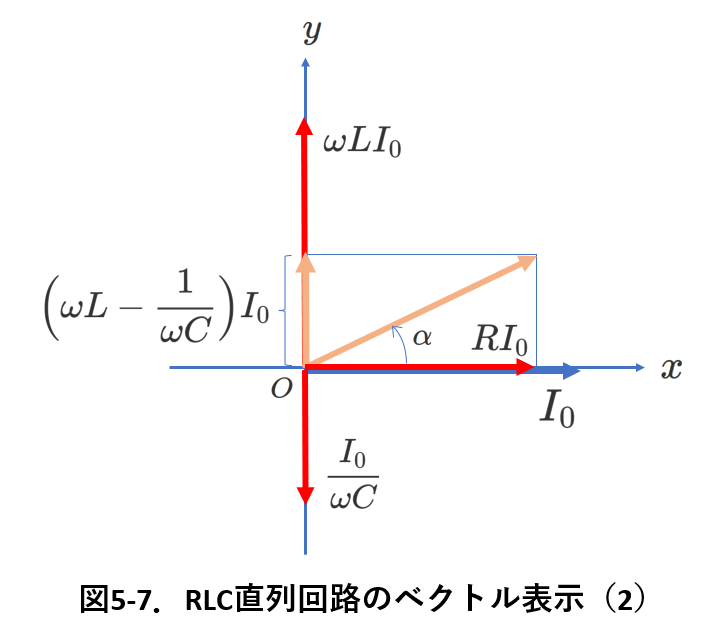
コンデンサーとコイルの電圧は符号が異なるだけですから,スカラー的に計算できます。
図5-7では,\(\omega L>\frac{1}{\omega C}\)の場合を図示しています。
この和と抵抗の電圧についてベクトルの足し算をします。このベクトルの長さ(最大値)は,
\(I_0\sqrt{(\omega L-\frac{1}{\omega C})^2+R^2}\)です。
そして,\(\tan\alpha=\frac{\omega L-\frac{1}{\omega C}}{R}\)です。
数式で表すと,
\begin{equation} E=I_0\sqrt{(\omega L-\frac{1}{\omega C})^2+R^2}\sin(\omega t+\alpha) \tag{5-5} \label{coil5-5} \end{equation}
ベクトル表示を使わなくても,三角関数の計算をすれば,同じ答が得えられます。
つまり,
\begin{eqnarray} E&=&\omega LI_0\sin(\omega t+\frac{\pi}{2})+RI_0\sin\omega t+\frac{I_0}{\omega C}\sin(\omega t-\frac{\pi}{2}) \\
&=& \omega LI_0\sin(\omega t+\frac{\pi}{2})+RI_0\sin\omega t-\frac{I_0}{\omega C}\sin(\omega t+\frac{\pi}{2}) \\
&=& (\omega L-\frac{1}{\omega C})I_0\sin(\omega t+\frac{\pi}{2})+RI_0\sin\omega t \\
&=&I_0\sqrt{(\omega L-\frac{1}{\omega C})^2+R^2}\sin(\omega t+\alpha)
\end{eqnarray}
ところで,
回路全体を流れる電流\(I=I_0\sin\omega t\),
回路全体に加わる電圧\(E=V_0\sin(\omega t +\phi)\),
とおいて,回路全体の交流に対する抵抗のはたらきを\(Z=\frac{V_0}{I_0}\)で表したとき,\(Z\)をこの回路のインピーダンスと言います。
(\ref{coil5-5})式から,RLC直列回路のインピーダンス\(Z_p\)は,
\begin{equation} Z_p=\sqrt{(\omega L-\frac{1}{\omega C})^2+R^2} \tag{5-6} \label{coil5-6} \end{equation}
となります。
これを,
\begin{equation} I_0=\frac{V_0}{Z}=\frac{V_0}{\sqrt{(\omega L-\frac{1}{\omega C})+R^2}} \end{equation}
と考えると,交流電圧の周波数を変化させると(\(V_0\)=一定として),\(I_0\)が変化することがわかります。
そして,特定の周波数で大きな電流が流れます。これを共振といいます。
共振の条件は,(\ref{coil5-6})式で分母が最小になることです。
つまり,
\begin{eqnarray} \omega L-\frac{1}{\omega C}=0 \\
\omega^2=\frac{1}{LC} \\
\omega=\frac{1}{\sqrt{LC}}
\end{eqnarray}
共振回路は,ラジオやテレビの電磁波の受信回路などに利用されています。
\(E\)(\(V_0\))に様々な角周波数の信号が混じっていても,この回路で特定の角周波数の信号を取り出すことができます。
4-2.RLC並列回路
では,次の例として,図5-8のRLC並列回路を考えます。
まず,共通なものを探します。
コイル,抵抗,コンデンサーの電圧\(V_0\)が等しいことに気が付きます。
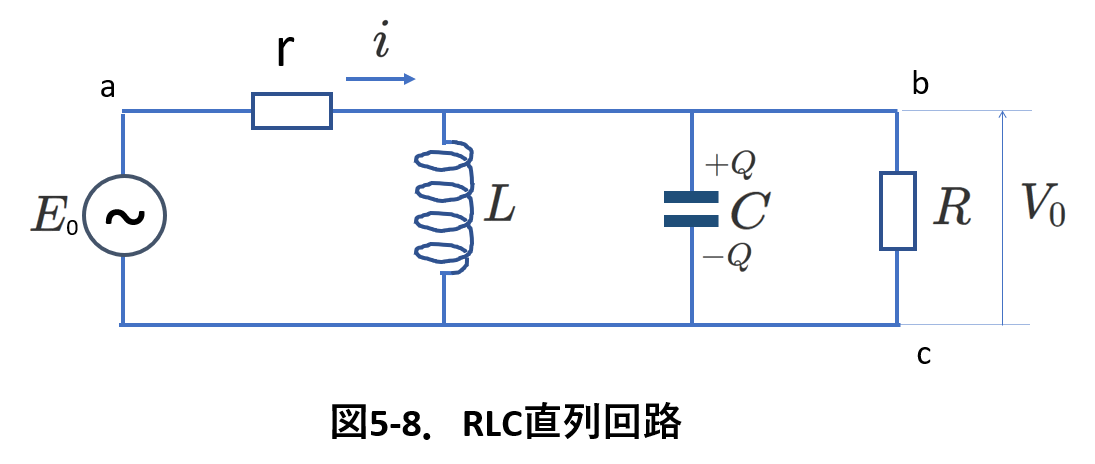
そこで,コイル,抵抗,コンデンサーの電圧を\(V_0\sin\omega t\)とします。
図5-9に回路のベクトル図を示します。
リアクタンスを用いて,
抵抗を流れる電流の大きさは,\(\frac{V_0}{R}\)で,位相は\(V_0\)と同じ,
コイルを流れる電流の大きさは,\(\frac{V_0}{\omega L}\)で,位相は\(V_0\)より\(\frac{\pi}{2}\)遅れ,
コンデンサーを流れる電流の大きさは,\(\omega CV_0\)で,位相は\(V_0\)より\(\frac{\pi}{2}\)進みます。
これは図5-9で②として表されています。
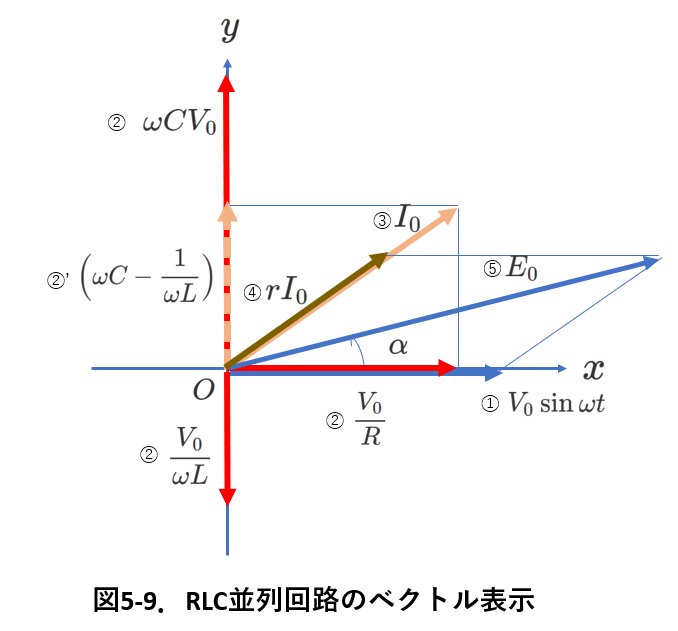
この3つの電流を足したもの(大きさ\(I_0\))が,電源から流れ出て抵抗\(r\)を流れる電流になります。
これを,③で示しました。
抵抗rでの電圧降下は,その大きさは\(rI_0\)で,位相は\(I_0\)と同じですから,図5-9の④のように描かれます。
それで,電源の電圧\(E_0\)は,\(V_0\)と\(rI_0\)のベクトル和ですから,図5-9の⑤となります。
ただし,出題されるものは,ここまで複雑なものはなく,抵抗\(r\)がないものが多いです。また,\(r\)が入っていたとしても,②までで終わることが多いです。
抵抗\(r\)がない場合については,電源の電圧が\(V_0\sin\omega t\)で表されたとき,電源から流れる電流を求めよというような問題となります。
5.電気振動回路
重要な交流回路のひとつに電気振動回路(LC共振回路)があります。
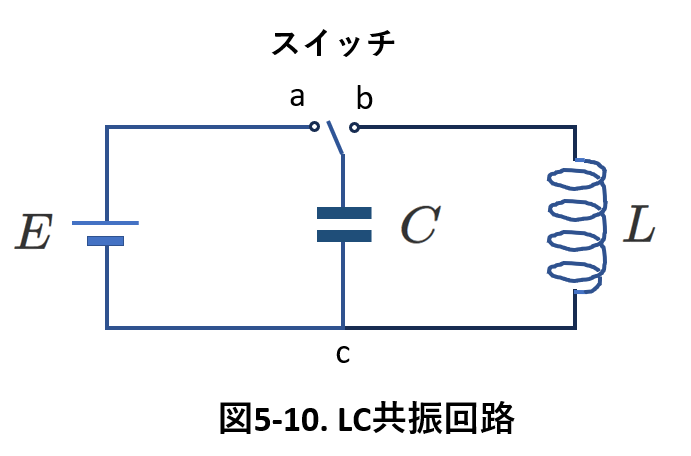
これを図5-10に示します。コンデンサーとコイルが直流電源\(E\)に対して,並列に接続されています。
まず,スイッチを\(a\)に倒してコンデンサー\(C\)に充電します。時間が経って\(Q\)の電荷が\(C\)に蓄えられます。(図5-11(1))
.png)
次にスイッチを\(b\)に倒します。
.png)
回路は直流電源から切り離されて,コンデンサーとコイルが並列につながった回路になりました。(図5-11(2))
さて,この回路について回路の方程式を立てます。
まず,図5-11(2)のように,\(i\)の正の向きを定めます。
これは,コンデンサーに蓄えられた電荷がコイルをつないだことで,図の向きに流れると思われるからです。
そして,コンデンサーの正の向きを電流が流れ込む向きを正とします。
つまり,図5-11(2)で+-を付加したとうりです。
この決め方はなんとなく変(今+電荷が蓄えられている極板を負に設定している)と感じるかもしれませんが,図5-5でコンデンサーの正負を決めた考え方と同じです。
では,回路の方程式を立てます。
任意の時刻\(t\)において,電流が\(i\),コンデンサーの電荷が\(q\)(+極板側が\(+q\))と考えて,
\begin{eqnarray}
-L\frac{di}{dt}&=&\frac{q}{C} \tag{5-7} \label{coil5-7} \\
これは,コイルの自己誘導起電力をもとに立てた式です。 \\
コイルを電圧降下素子として式を立てると, \\
0&=&L\frac{di}{dt}+\frac{q}{C} \\
また,i&=&\frac{dq}{dt} \tag{5-8} \label{coil5-8}
\end{eqnarray}
(\ref{coil5-8})式の符号を確認します。,\(q\)が増えるときは,\(i\)が正の向きに流れたときですから,この符号で正しいことがわかります。
上記2つの式から,
\begin{eqnarray}
-L\frac{d}{dt}(\frac{dq}{dt})&=&\frac{q}{C} \\
LC\frac{d^2q}{dt^2}&=&-q \\
\frac{d^2q}{dt^2}&=&-\frac{q}{LC} \tag{5-9} \label{coil5-9}
\end{eqnarray}
(\ref{coil5-9})式は,\(ma=-kx\),つまり,\(\frac{d^2x}{dt^2}=-\frac{k}{m}x\)と式の形が同じです。
式の形が同じですから,解も同じ形になります。
つまり,\(q\)は振動します。
その周波数\(f\)は,
\begin{eqnarray} \frac{d^2q}{dt^2}&=&-\frac{1}{LC}q \ より, \omega^2=\frac{1}{LC} \\
ゆえに,\omega&=&\frac{1}{\sqrt{LC}} \tag{5-10} \label{coil5-10} \\
f&=&\frac{1}{2\pi\sqrt{LC}} \end{eqnarray}
振動中心は,\(q=0\)です。
ここで大事なことは,\(\omega\)は\(L\)と\(C\)の値から一義的に決まるということです。
\(L\)と\(C\)が決まっていれば,決まった\(\omega\)で振動します。
図5-11(1)から,スイッチを\(b\)に倒したときを,時刻\(t=0\)として,このときのコンデンサーの電荷\(Q\)が振動の最大値になります。
そこで,\(Q\)をあらためて\(Q_{MAX}\)とします。
また,コンデンサーの極板の正負から,\(q\)の振動は\(-\cos\)型だとわかりますから,\(q\)は,
\begin{equation} q=-Q_{MAX}\cos\omega t \tag{5-11} \label{coil5-11} \end{equation}
これより,
\begin{eqnarray} i&=&\frac{dq}{dt}=\omega Q_{MAX}\sin\omega t \tag{5-12} \label{coil5-12} \\
V_L&=&-L\frac{di}{dt}=-\omega^2 LQ_{MAX}\cos\omega t
\end{eqnarray}
となります。
以上の計算をもとに,ここで,コンデンサーの静電エネルギーとコイルの電磁エネルギーの和を求めておきましょう。
(\ref{coil5-11})式と(\ref{coil5-12})式を用いて,
\begin{eqnarray} \frac{1}{2}CV_L^2+\frac{1}{2}Li^2&=&\frac{1}{2}qV_L+\frac{1}{2}Li^2 \\
&=&\frac{1}{2}(-\omega^2LQ_{MAX}\cos\omega t)(-Q_{MAX}\cos\omega t)+\frac{1}{2}L(\omega Q_{MAX}\sin\omega t)^2 \\
&=&\frac{1}{2}\omega^2LQ^2_{MAX}\cos^2\omega t+\frac{1}{2}\omega^2LQ^2_{MAX}\sin^2\omega t \\
&=&\frac{1}{2}\omega^2LQ^2_{MAX} \\
&=&\frac{1}{2}\frac{1}{LC}LQ^2_{MAX} (なぜなら, \omega^2=\frac{1}{LC} ) \\
&=&\frac{Q^2_{MAX}}{2C}=一定
\end{eqnarray}
全ての瞬間で回路のエネルギー保存則が成り立つことが証明されました。
コンデンサーの静電エネルギーとコイルの磁気エネルギーの和は,最初にコンデンサーに蓄えられていた静電エネルギーに等しいです。
ここで,少し前に戻って,図5-11(2)の回路で,コンデンサーの極板の正負を逆に定めた場合に回路の方程式がどうなるかを調べます。
初期に+電荷が溜まっていた上側の極板を正にしたくなるので確認しておきます。
この回路図を図5-11(3)に示します。
.png)
コンデンサーの正負を確認してください。
上側の極板を正と定めています。
このとき,コイルの自己誘導起電力は以前と同じで\(-L\frac{di}{dt}\)です。
一方,定めた電流に対して,コンデンサーの正負は逆ですから,電圧降下は\(-\frac{q}{C}\)です。
重要なのは,電流\(i\)とコンデンサーの電荷\(q\)との関係です。
これは,\(i=-\frac{dq}{dt}\)です。
\(q\)が減少したとき(\(\frac{dq}{dt}<0),したがって,-\frac{dq}{dt}>0\)),\(i\)が正の向きに流れるので負号がつきます。
これより,
\begin{eqnarray} -L\frac{di}{dt}&=&-\frac{q}{C} \\
i&=&-\frac{dq}{dt} \\
以上2式より,L\frac{d}{dt}(-\frac{dq}{dt})&=&\frac{q}{C} \\
L\frac{d}{dt}(-\frac{dq}{dt})&=&\frac{q}{C} \\
\frac{d^2q}{dt^2}&=&-\frac{1}{LC}q
\end{eqnarray}
(\ref{coil5-9})式と同じ振動の式が得られました。
.png)
次に,図5-11(4)を参照して下さい。
1周期分の振動に対して,\(t=0, \frac{1}{4}T, \frac{2}{4}T, \frac{3}{4}T, T\)でのコンデンサーの電荷\(q\)とコイルの電流\(i\)がどのように変化していくかを表しています。
コンデンサーの電荷が\(0\)のとき,コイルの電流は最大,あるいは最小になります。
コンデンサーの電荷が最大,あるいは最小のとき,コイルの電流は\(0\)です。
\(t=0\)でコンデンサーに充電された電荷が流れ始めますが,コイルは電流を\(0\)に維持しようとしますから,電流は\(0\)からは徐々に増加して,コンデンサーの電荷が\(0\)になったとき,コイルの電流が最大になります。
ここで一瞬,コイルの電流は一定,すなわち,電圧は\(0\)になります。
ただ,コイルの電圧が\(0\)になっても電流はすぐには\(0\)にはなりません。
コイルの性質として,この電流を維持しようとするので,電流は減少しながら流れ続け,コンデンサーには\(t=0\)の電荷と逆の極性の電荷が溜まります。
この1周期のどの瞬間でもエネルギーの保存則が成り立つので,コンデンサーの電荷が\(0\)のとき,したがって,コンデンサーの静電エネルギーが\(0\)のときには,最初の静電エネルギーはすべてコイルの電磁エネルギー\(\frac{1}{2}LI^2_{MAX}\)に変化したと考えられます。
ちなみに,この回路は,角周波数\(\omega\)の交流電流を作る回路で発信回路です。
\(LC\)を変えることで,\(\omega\)を変化させることができます。
この共振回路と抵抗\(r\)と交流電源を組み合わせた,図5-12の回路を考えます。
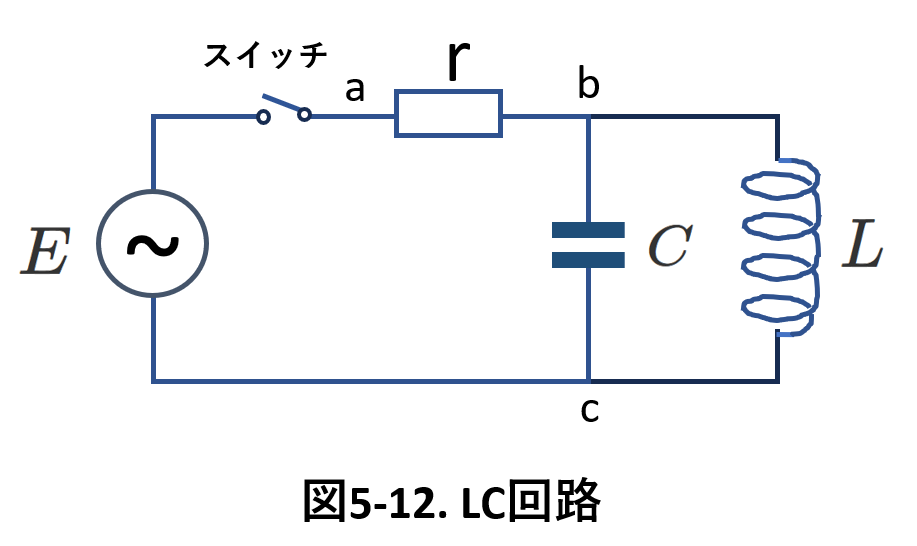
スイッチを閉じたあと,定常状態になったときの抵抗\(r\)に流れる電流について考えます。
コンデンサーとコイルが並列なので,これらの素子に加わる電圧(cに対するbの電圧)を\(V_0\sin\omega t\)と仮定します。
このとき,交流電源の角周波数を\(\omega\)として,
コイルを流れる電流は,\(\frac{V_0}{\omega L}\sin(\omega t-\frac{\pi}{2})\),
コンデンサーを流れる電流は,\(\omega CV_0\sin(\omega +-\frac{\pi}{2})\)
です。
したがって,\(r\)を流れる電流\(i\)は,ふたつの電流の和で求められます。
\begin{eqnarray} i&=&\frac{V_0}{\omega L}\sin(\omega t-\frac{\pi}{2})+\omega CV_0\sin(\omega t+\frac{\pi}{2}) \\
&=&\frac{V_0}{\omega L}(-\cos\omega t)+\omega CV_0(\cos\omega t) \\
&=&(\omega C-\frac{1}{\omega L})V_0\cos\omega t \tag{5-13} \label{coil5-13}
\end{eqnarray}
共振条件が成り立つ場合,つまり,\(\omega=\frac{1}{\sqrt{LC}}\)のとき,(\ref{coil5-13})式は\(0\)になります。
つまり,抵抗\(r\)には電流は流れません。
したがって,コンデンサーとコイルには電源の電圧がそのまま加わっています。
抵抗\(r\)の電流は\(0\)であっても,コイルとコンデンサーには電流は流れています。
図5-11(4)で示したと同じように,コイルからコンデンサーに,コンデンサーからコイルへと,コイルとコンデンサーの回路の中で電流は循環しています。
コイルとコンデンサーを流れる電流の向きが逆になっていることを,コイルとコンデンサーを流れる電流の式から確認してください。
関連ページ
- コンデンサーを理解する
- コンデンサについて学んでおくべき内容のうち、コンデンサーの性質を説明しています。
- 電磁気公式
- 電磁気の公式をまとめています。