運動方程式

Ⅰ．等加速度運動の運動方程式

　物体にはたらく力を\(F\)、時刻を\(t\)、質量を\(m\)、座標を\(x\)、速度を\(v\)、加速度を\(\alpha\)として、
この物体の運動方程式は、\(m\alpha=F\)と表されます。
　微分形式で、正確に書くと、
\begin{eqnarray} m\frac{d^2x(t)}{dt^2}&=&F(x,t)　\tag{1-1} \\
ここで、\alpha&=&\frac{d^2x(t)}{dt^2}
\end{eqnarray}
です。
　一般的に、\(F\)は\(座標xと時刻t\)の関数です。
（1-1）式は2階の微分方程式で、これを解けば時間経過により、
物体の位置と速度がどのように変化するかを予測することができます。
しかし、高校レベルでは、この2階の微分方程式は特別な場合を除いて解くことができません。

　そこで、高校の物理では、運動方程式を解くことはしないで、
それぞれの運動方程式の形に応じた利用をすることになります。

　さて、高校のレベルで解くことのできる運動方程式は、
\(F\)が位置や時間に依らず、一定の場合です。つまり、等加速度運動の場合です。
\begin{eqnarray} m\frac{d^2x(t)}{dt^2}&=&F　（Fは定数）　\tag{1-2} \\
\frac{d^2x(t)}{dt^2}&=&\frac{F}{m} \tag{1-2'}
\end{eqnarray}

　では、これを解いてみます。
（1-2'）式の両辺を積分すると、積分定数\(C_1\)として、
\begin{eqnarray} \frac{dx(t)}{dt}&=&C_1+\frac{F}{m}t \\
t=0のとき&、& \frac{dx(0)}{dt}=v_o（v_oは初速）とすると、C_1=v_o が得られて　\\
\frac{dx(t)}{dt}&=&v_o+\frac{F}{m}t \tag{1-3} \\
\frac{F}{m}=\alpha とおいて、\frac{dx(t)}{dt}&=&v_o+\alpha t \tag{1-3'} \\
\\
さらに&、&tで積分して、その積分定数をC_2として、 \\
x(t)&=&C_2+v_ot+\frac{1}{2}\alpha t^2 \\
t=0のとき&、&x(0)=x_oとすれば、　　　\\
x(t)&=&x_o+v_ot+\frac{1}{2}\alpha t^2 \\
\end{eqnarray}

　毎回、微分方程式を解いたのでは時間がかかるので、
この運動が等加速度運動であるとわかったあとは、たいへん有用で重要な次の公式を用います。

\begin{eqnarray} v&=&v_o+\alpha t \\
x&=&x_o+v_o t+\frac{1}{2}\alpha t^2 \\
v^2-v_o^2&=&2\alpha\left(x-x_o\right) \\
\\
ただし、時刻t&=&0での速度はv_o、x座標はx_0、　\\
時刻tでの加速度は\alpha、速度はv&、&x座標はx、速度と加速度は+xの向きが正
\end{eqnarray}

Ⅱ．単振動の運動方程式

　単振動の運動方程式は、次の形で表されます。
おもりの質量を\(m\)、加速度を\(\alpha\)、座標を\(x\)、ばねのばね定数を\(k\)として、
\begin{equation} m\alpha=-k(x-x_o) \tag{2-1} \end{equation}
ここで、\(x_o\)は、振動の中心です。

　\(x_o\)が、振動の中心であることは、次のように考えます。
(2-1)式に\(x=x_o\)を代入すれば、\(\alpha=0\)です。
加速度が\(0\)となる瞬間は、おもりが振動の中心にあるときです。
また、加速度が\(0\)となる瞬間は、力がつりあっているときであり、それはおもりが単振動の中心にあるときです。

　さて、(2-1)式を微分形式で表すと、次のようになります。
\begin{eqnarray} m\frac{d^2x(t)}{dt^2}&=&-k\left(x(t)-x_o\right)　\tag{2-2} \\
ここで&、&\alpha=\frac{d^2x(t)}{dt^2} \\
加速度の式は&、&\frac{d^2x(t)}{dt^2}=-\frac{k}{m}\left(x(t)-x_o\right) \tag{2-3}
\end{eqnarray}

　（2-3）式より、\(x(t)\)を2階微分すると、もとの関数\(x(t)\)を定数倍したものとなり、符号が変わることがわかります。
このことから、\(x(t)\)は、三角関数だと予想できます。
そこで、\(x(t)=A\sin{(\omega t+\phi)}+x_o\)として、（2-3）式の左辺に代入してみます。
（ここで、\(\omega\)は単振動の角周波数）

\begin{eqnarray} \frac{d^2x(t)}{dt^2}=-\omega^2A\sin(\omega t+\phi) \\
右辺に代入すると、-\frac{k}{m}\left(A\sin\left(\omega t+\phi\right)+x_o-x_o\right) =-\frac{k}{m}A\sin\left(\omega t+\phi\right) \\
以上より、\omega^2=\frac{k}{m} であれば、A\sin\left(\sqrt{\frac{k}{m}}t+\phi\right) は（2-3）式の解であることがわかります。
\end{eqnarray}

つまり、物体（おもり）について、次の運動方程式（2-1）が成り立つとき、
\begin{equation} m\alpha=-k(x-x_o) \tag{2-1} \end{equation}
物体（おもり）の運動は単振動となり、
振動の中心の座標は\(x_o\)、
角周波数\(\omega\)は、
\begin{eqnarray} \alpha=-\frac{k}{m}(x-x_o)=-\omega^2(x-x_o) \\
と考えて、\omega=\sqrt{\frac{k}{m}}
\end{eqnarray}

【単振動の運動方程式の使い方】
単振動の運動方程式(微分方程式）を直接解くことはありません。
運動方程式の形だけから、単振動かどうかの判定をします。
単振動であることがわかれば、運動方程式から、振動の中心や角周波数が読み取れます。

　場合によっては、立式した「運動方程式」を「単振動の運動方程式」に近似して、そこから単振動の角周波数等を求める問題もあります。
　このような場合は、近似式の使い方がポイントですが、近似して導く「単振動の運動方程式」の形を頭に描いて、式を変形するのが良い方法です。

　ところで、力学的エネルギー保存の式から運動方程式を導くことができます。
単振動の場合、力学的エネルギー保存の式は、
（\(x_o\)をばねが自然長のときのおもりの座標として）
\begin{eqnarray} &&\frac{1}{2}mv^2+\frac{1}{2}k(x-x_o)^2=[一定]　\\
速度vと座標x&が&時間の関数であることに注意して、両辺を時間tで微分します。　\\
&&\frac{1}{2}m\times 2v\frac{dv}{dt}+\frac{1}{2}k\times 2(x-x_o)\frac{d(x-x_o)}{dt}=0　\\
&&mv\frac{dv}{dt}+k(x-x_o)\frac{dx}{dt}=0 \\　
&&mv\alpha+k(x-x_o)v=0　\\
&&m\alpha=-k(x-x_o)　\\
\end{eqnarray}
以上のように、運動方程式が導かれました。

Ⅲ．円運動の運動方程式

　等速円運動では、速度の大きさ（すなわち速さ）は一定ですが、向きが常に変わるため、速度は変化します。
つまり、加速度を持ちます。

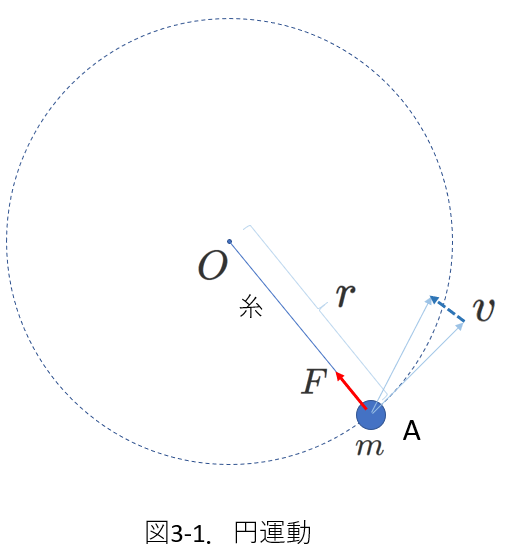
　右の図を参照してください。
糸の一方が点Oで固定され、他の一方につながれたおもりAが、水平な台上で点Oの周りで円運動をしています。
　糸がなければ、Aは円運動の接線の方向に等速直線運動をするはずですが、
常に円運動の中心に向かう向きにはたらく力によって、その向きに速度が変化します。
この力によるおもりAが持つ加速度\(\alpha\)の大きさは、円運動の半径を\(r\)、速さを\(v\)、角速度を\(\omega\)として、\(r\omega^2\)、または、\(\frac{v^2}{r}\)と表され、向きは円運動の中心に向かう向きです。

　図3-1では、Aに、中心に向かう力\(F\)がはたらくと考えています。
これが、向心力です。

　\(F\)の向心力がはたらいて、質量\(m\)のおもりAが、\(r\omega^2\)、または、\(\frac{v^2}{r}\)の加速度を持つわけですから、
円運動の運動方程式は、
\begin{eqnarray} mr\omega^2=F \tag{3-1} \\
m\frac{v^2}{r}=F \tag{3-2}
\end{eqnarray}
と表されます。

　ところで、後述の鉛直面内での円運動は、速度が時間経過にしたがって変化して、
等速円運動ではありませんが、上の2式は成立します。

　ある瞬間に半径が\(r\)、速さが\(v\)（または、角周波数が\(\omega\)）、はたらく力が\(F\)であれば、
その瞬間について上の2つの運動方程式が成立します。

また、等速円運動について重要な式は、
\begin{eqnarray} 周期　　&&T=\frac{2\pi r}{v}=\frac{2\pi}{\omega} \tag{3-3}　\\
速さ　　&&v=r\omega \tag{3-4}
\end{eqnarray}

　さて、円運動の運動方程式の使い方ですが、
「運動方程式を立てたら、円運動であることがわかった」という使い方はありません。
既に円運動であることがわかっている運動に対して、円運動の運動方程式を立て、
その運動方程式のパラメータのひとつ、あるいは二つを求めるという使い方がほとんどです。

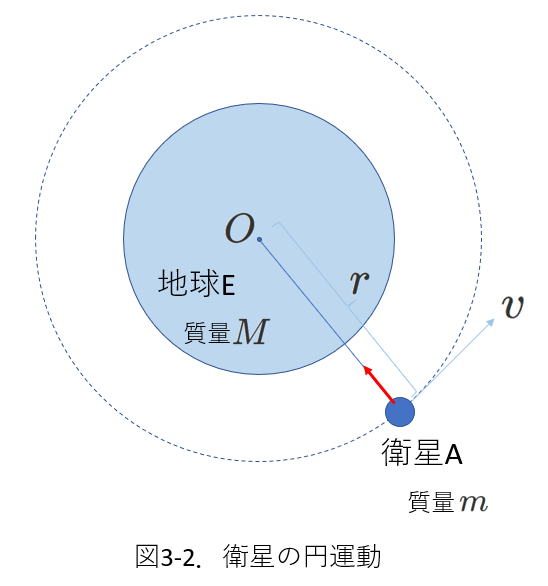
（１）最初の例は、地球の周りをまわる人工衛星です。

　図3-2では、質量\(M\)の地球Eの周りを、地球の重心から\(r\)の距離のところで、質量が\(m\)の人工衛星Aが速さ\(v\)の等速円運動をしています。

　地球Eと衛星Aの間には、万有引力がはたらきます。
地球にも万有引力がはたらくので、厳密には、衛星は地球の重心の周りで円運動をするわけではありませんが、地球の質量が衛星の質量に比べて極めて大きいため、地球はほとんど動かないと考えて、衛星は地球の重心の周りで等速円運動をすると考えることができます。

　地球Eと衛星Aの間にはたらく万有引力（すなわち、向心力）の大きさは、
万有引力定数を\(G\)として、\(G\frac{mM}{r^2}\)です。
したがって、運動方程式は、
\begin{equation} m\frac{v^2}{r}=G\frac{mM}{r^2} \tag{3-5} \end{equation}
　問題で問われるものは、\(r\)、または、\(v\)です。
まれに、\(G\)の値を求めるものもあります。
（3-5）式をもとに、上に挙げた３つのパラメータを求めてみます。
\begin{eqnarray} r&=&\frac{GM}{v^2} \tag{3-6} \\
v&=&\sqrt{\frac{GM}{r}} \tag{3-7} \\
G&=&\frac{rv^2}{M} \tag{3-8}
\end{eqnarray}

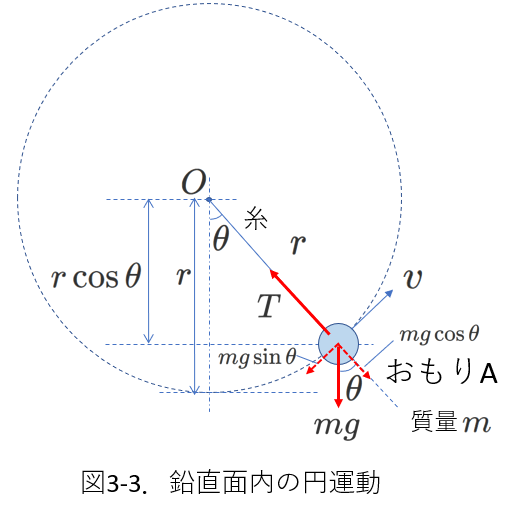
（２）鉛直面内の円運動

　図3-3では、一方の端を点\(O\)に固定された糸の他端におもりAがつながれ、Aが円運動をしています。
図3-1と異なり、おもりは鉛直な面の中で円運動をしています。
（つまり、図3-3上で下向きに重力がはたらきます。）

　図3-1は水平な台上での円運動です。
おもりAには向心力\(F\)以外に重力がはたらきますが、
台からの垂直抗力が重力と逆向きにはたらき、
鉛直方向には力がつりあっていると考えることができます。

　また、図3-2では、向心力となる万有引力以外の力ははたらきません。

　図3-1の力\(F\)や図3-2の万有引力は一定であること、
それ以外の力がはたらかないか、または、それ以外の力同士でつりあっているため、円運動は等速円運動でした。

　図3-3の鉛直面内の円運動はこれらとは異なり、等速ではありません。
図3-3で、おもりは円運動をすることがわかりますから、円運動の運動方程式を立てることができます。

　今、糸が図3-3にあるように鉛直方向から角度\(\theta\)だけ傾いているとき、
糸の張力が\(T\)、おもりAの速さが\(v\)であったとすると、
向心力は、円運動の中心に向かう向きの力ですから、この瞬間の向心力は、\(T-mg\cos\theta\)であることがわかります。

　したがって、円運動の運動方程式は、
\begin{eqnarray} m\frac{v^2}{r}=T-mg\cos\theta \tag{3-9} \\
または、mr\omega^2=T-mg\cos\theta \tag{3-10}
\end{eqnarray}
となります。

　重力\(mg\)の向心力に垂直な成分\(mg\sin\theta\)は、円の接戦方向にはたらき、
図3-3のおもりAの近傍では、おもりAの進む向きとは逆向きにはたらくため、おもりAに対して負の仕事をすることになり、
おもりAの運動エネルギーは減少します。
　このことは、おもりAの高さが高くなると、位置エネルギーが増加するので、その分だけ運動エネルギーが減少すると説明することもできます。
これらの考察から、この場合の円運動は等速ではないとわかります。

　（3-9）式を利用する問題で問われるものは、\(T\)と\(v\)です。
未知数ふたつですから、これらを求めるためには、もうひとつの条件、あるいは、方程式が必要です。
それには、力学的エネルギー保存則を利用します。

　たとえば、おもりAが鉛直真下にあるとき、Aの速さが\(v_o\)であったとすると、
そのときのおもりAの位置を位置のエネルギーの基準として、次の力学的エネルギー保存則が立式できます。
\begin{equation} \frac{1}{2}mv_o^2+mg\times 0=\frac{1}{2}mv^2+mgr(1-\cos\theta) \tag{3-11} \end{equation}

　鉛直面内の円運動では、運動方程式（3-9）式、または（3-10）式と、力学的エネルギー保存の（3-11）式を組み合わて考察するのが定番です。
（3-11）式から\(v\)が求まり、それを（3-9）式に代入すれば、張力\(T\)が求められます。

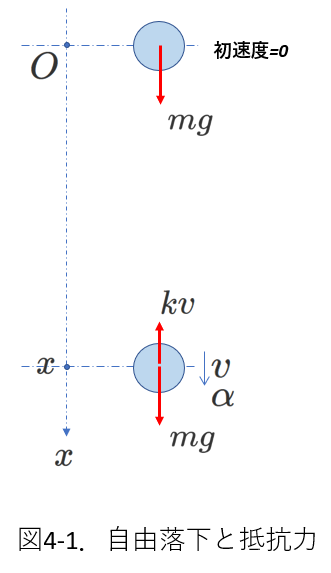
Ⅳ．速度に比例した力がある場合

　速度に比例した力の例は、物体が運動しているときに受ける抵抗力などです。
抵抗力ですから、運動している物体の速度\(v\)の向きと逆向きに力がはたらきます。

　右の図4-1では、質量\(m\)の物体が落下しています。
空気中を落下するとき、物体は空気から抵抗力を受けると考えて運動を考察します。

注）実際には、物体には空気による浮力もはたらきます。
　　しかし、浮力は、他の力と比較して小さいため、ここでは無視できると考えます。
　　空気の抵抗力も小さいですが、
　　重力で加速されて速度が大きくなると抵抗力も大きくなり、無視できなくなります。

　物体の\(x\)座標が\(x\)のときの速度を\(v\)、加速度を\(\alpha\)として、
物体にはたらく力は、
①重力\(mg\)は下向き、
②抵抗力は大きさが\(kv\)で、向きは上向きです。

　したがって、下向きを加速度の正の向きとして、
運動方程式は、
\begin{equation} m\alpha=mg-kv \tag{4-1} \end{equation}
となります。

　（4-1）式を微分形式で書くと、
\begin{eqnarray} m\frac{d^2x(t)}{dt^2}=mg-\frac{dx(t)}{dt} \\
m\frac{d^2x(t)}{dt^2}+\frac{dx(t)}{dt}=mg \tag{4-2}
\end{eqnarray}
となります。この微分方程式を解くのは難しく、問題で要求されることはありません。
　したがって、「速度に比例した力がある場合」の問題のパターンは決まっています。
多くの場合、時間が十分に経過したあとに、一定となった速度を問われます。

　さて、（4-1）式から、時間が経過すると速度が一定となることを考察します。
　時刻\(t=0\)において\(v=0\)ですから、（4-1）式から\(\alpha=g\)です。
時間が経過すると、速度\(v\)が大きくなるので、加速度\(\alpha\)は減少します。
そして、さらに速度\(v\)が大きくなると、抵抗力は重力と同じ大きさに達し、加速度\(\alpha=0\)となり、速度は一定となります。

　一定となったときの速度\(v'\)を求めるには、
ふたつの方法があります。

①ひとつは、(4-1)式で加速度\(\alpha=0\)とする方法で、
\begin{eqnarray} mg-kv'=0 \tag{4-2} \\
v'=\frac{mg}{k} \tag{4-3}
\end{eqnarray}

②ふたつめは、一定の速度（定速度運動）になったときは、力がつりあっていると考える方法です。
このとき、\(mg=kv'\)と表され、（4-3）式と同じ結果になります。

Ⅴ．運動方程式と保存則の違い

　運動方程式を使って解く場合と保存則を使って解く場合を比較します。

放物運動

　なるべく簡単な例を使うのがわかりやすいので、
「角度\(\theta\)、初速\(v\)でボールを投げた時の運動」を考えます。
このとき、ボールが最も高くあがったときの投げた地点からの高さ（最高点）と、投げてから最高点に到達するまでの時間を求めてみましょう。

（１）運動方程式を使う

　右図のように、2次元での運動ですから、\(x\)方向と\(y\)方向の運動方程式を立てます。
\(x\)方向の加速度を\(\alpha_x\)、\(y\)方向の加速度を\(\alpha_y\)とし、
それぞれの軸の\(+\)の向きを加速度の正の向きとして、
\begin{eqnarray} m\alpha_x&=&0 \\
m\alpha_y&=&-mg
\end{eqnarray}
となります。
　これより、\(\alpha_x=0\)、\(\alpha_y=-g\)　です。

\(x\)方向には等速度運動、\(y\)方向には等加速度運動ということがわかります。
　したがって、\(x\)方向の速度を\(v_x\)、\(y\)方向の速度を\(v_y\)として、
\begin{eqnarray} v_x&=&v\cos\theta \tag{5-1} \\
v_y&=&v\sin\theta+(-g)t \tag{5-2} \\
x&=&v\cos\theta\times t \tag{5-3} \\
y&=&v\sin\theta\times t+\frac{1}{2}(-g)t^2 \tag{5-4}
\end{eqnarray}

放物運動#2

　このように、等速度運動や等加速度運動の場合には、
運動方程式を利用すれば、加速度が求められ、
それにより、時刻\(t\)での速度と座標がわかります。

　では、上の式を使って、ボールが最も高くあがったときの、投げた地点からの高さ（最高点）\(y_{max}\)と、投げてから最高点に到達するまでの時間\(t_{max}\)を求めてみましょう。

（5-1）～（5-4）式からこの運動の軌跡は右図のような放物線です。

　では、3つの方法で求めてみます。
１．

最高点では、速度の\(y\)方向成分は0になる。
（しかし、このときでも、\(x\)成分は0でないことに注意しましょう。）

ことに気づけば、（5-2）式から\(t_{max}\)が計算できます。
\begin{eqnarray} 0&=&v\sin\theta+(-g)t_{max} \\
t_{max}&=&\frac{v\sin\theta}{g}
\end{eqnarray}

続いて（5-4）式の\(t\) に\(t_{max}\)を代入すれば、\(y_{max}\)も計算できます。
\begin{eqnarray} y_{max}&=&v\sin\theta\times \frac{v\sin\theta}{g}-\frac{1}{2}g\left(\frac{v\sin\theta}{g}\right)^2 \\
&=&\frac{v^2\sin^2\theta}{2g}
\end{eqnarray}

２．数学的に、平方完成の形に表して、（4）式の最大値を求めます。
\begin{eqnarray}
y&=&v\sin\theta\times t+\frac{1}{2}(-g)t^2 \tag{5-4} \\
&=&-\frac{1}{2}g\left(t^2-\frac{2v\sin\theta\times t}{g} \right) \\
&=&-\frac{1}{2}g\left(t-\frac{v\sin\theta}{g} \right)^2 +\frac{v^2\sin^2\theta}{2g}
\end{eqnarray}

つまり、\(t=\frac{v\sin\theta}{g} のとき、yの最大値は、\frac{v^2\sin^2\theta}{2g}\)　です。

１．は物理的な意味から求めています。　
２．は（5-4）式が求められたところで数学的扱いに代わっているところが面白いです。
この二通りの求め方は、色々なところで見られます。

３．また、加速度がわかっているので、\(y\)方向について次の公式を使って\(y_{max}\)を求めることができます。
\begin{eqnarray} 0^2-(v\sin\theta)^2&=&2(-g)y_{max} \tag{5-5} \\
y_{max}&=&\frac{v^2\sin^2\theta}{2g}
\end{eqnarray}

（2）力学的エネルギー保存則を使う

　力学的エネルギー保存則を使う場合は、一般的に、
　「力学的エネルギーを計算しやすい瞬間の、力学的エネルギーの和」=「求めるべき瞬間の力学的エネルギーの和」
という式を立てます。ここでは、
　「投げる瞬間のボールの力学的エネルギーの和」=「最高点に達したときのボールの力学的エネルギーの和」
とするのが適切です。
　最高点では、速度の\(y\)成分は\(0\)ですが、\(x\)成分は\(0\)ではなく、\(v\cos\theta\)です。
（間違えて、\(0\)にしないようにしましょう。）

　重力の位置エネルギーの基準を\(y=0\)にすると、力学的エネルギー保存を表す式は、
\begin{eqnarray} \frac{1}{2}mv^2+mg\times0&=&\frac{1}{2}m(v\cos\theta)^2+mg\times y_{max} \tag{5-6} \\
\frac{1}{2}m(v^2\cos^2\theta+v^2\sin^2\theta)&=&\frac{1}{2}mv^2\cos^2\theta+mg\times y_{max} \\
これより、　y_{max}&=&\frac{v^2\sin^2\theta}{2g} \end{eqnarray}

注1）　左辺の\(mg\times0\)は書く必要はありませんが、
0であっても常に運動エネルギーと重力による位置エネルギーを式に表すと決めておくと
どちらかのエネルギーの項を忘れるというミスを防ぐことができます。
また、答案を見直す際にもわかりやすいので、お薦めです。

注2）　上の（5-6）式は(5-5)式と等価です。教科書では（5-5）式から、「運動エネルギーと仕事の関係」を導き、さらに「力学的エネルギー保存則」を導いています。ですから、同じ形になります。

　上の式を見てもわかりますが、力学的エネルギー保存則を利用する場合は、
その運動について理解していなければなりません。
この状況で言えば、
最高点に達したときのボールの速さが\(v\cos\theta\)であることを理解していないと式が立てられません。

　その点が理解できていれば、\(y_{max}\)を求めるには、力学的エネルギー保存則を使うのが便利です。
投げてから最高点に至る過程（運動）の詳しい考察なしに、最高点にある状態について答えが得られます。
ただし、（5-6）式から\(t_{max}\)は得られません。

　力学的エネルギー保存からは外れてしまいますが、
\(t_{max}\)は、力積と運動量の変化の関係から求めることができます。
ボールに働く力は一定で\(-mg\)ですから、力積\(-mg\times t_{max}\)により、
ボールの運動量の\(y\)方向成分が、\(mv\sin\theta\)から\(m\times 0\)に変化したということを式に表して、
\begin{eqnarray} m\times 0-mv\sin\theta&=&-mg\times t_{max} \tag{7} \\
t_{max}&=&\frac{v\sin\theta}{g}
\end{eqnarray}

Ⅵ．運動方程式を立てる軸と制約条件

１．固定された斜面上の物体の運動

　右図のように固定された斜面上をすべる物体Aを考えます。
Aと斜面の間には摩擦はありません。

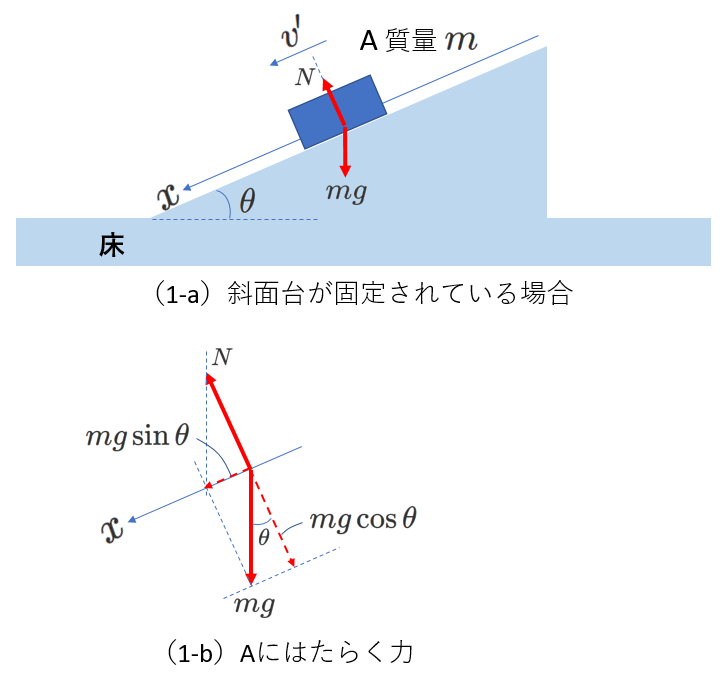
固定された斜面上の物体の運動

　さて、物体Aの運動方程式を立てる場合、どの方向の式を立てたらよいでしょうか。

　Aは、斜面に沿ってのみ動くことができます。
したがって、斜面に沿って、下向きを正とする\(ｘ\)軸を設定して運動方程式を立てるのがよいです。
　\(x\)軸に垂直な方向には、動くことができません。つまり、その方向にAにはたらく力は釣り合っているはずです。

右図（1-b）を参照すると、Aにはたらく力の合力の\(x\)軸方向の成分は、\(mg\sin \theta\) であることがわかります。
したがって、運動方程式は、Aの加速度を\(\alpha\)として、
\begin{equation} m\alpha=mg\sin \theta \tag{5-1} \end{equation}
となります。これより、
\begin{equation} \alpha=g\sin \theta \tag{5-2} \end{equation}
です。

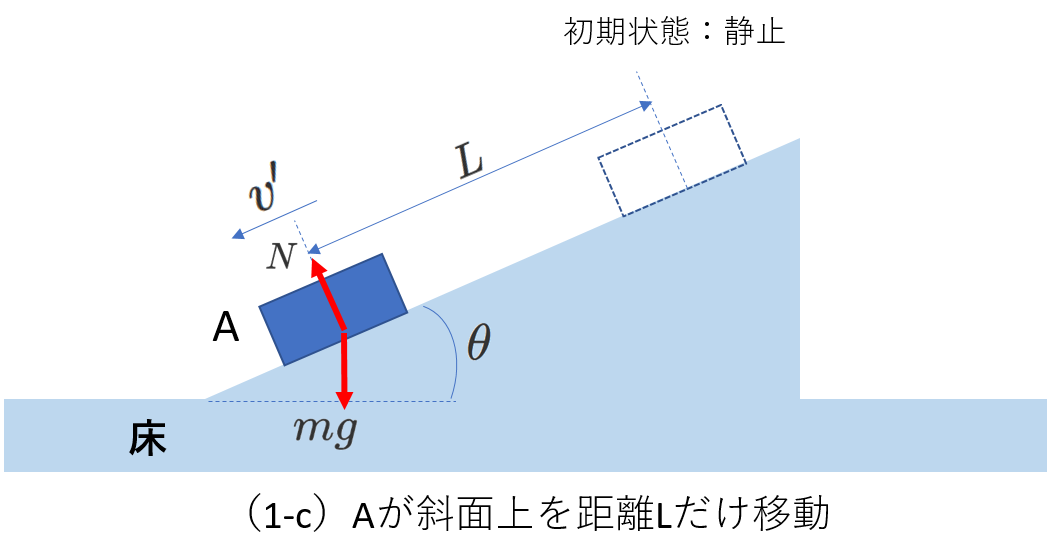
固定された斜面上の物体が距離Lだけ移動

　ここで、図(1-c)のように、静止していた物体Aが、斜面に沿って距離Lだけ滑り降りたときの、Aの速さ\(v'\)を求めてみましょう。
\begin{eqnarray} v'^2-0^2&=&2\alpha L=2\left(g\sin\theta\right)L \tag{5-3} \\
v'&=&\sqrt{2gL\sin\theta} 　　\tag{5-4}　　\end{eqnarray}

　ここでは、次の等加速度運動の重要な関係式の3番目の式を使っています。

\begin{eqnarray} v&=&v_o+\alpha t \\
y&=&y_o+v_o t+\frac{1}{2}\alpha t^2 \\
v^2-v_o^2&=&2\alpha\left(y-y_o\right) \\
\\
ただし、時刻t&=&0での速度はv_o、y座標はy_0、　\\
時刻tでの加速度は\alpha、速度はv&、&y座標はy、速度と加速度は+yの向きが正
\end{eqnarray}

　さて、\(v'\)は、次のように力学的エネルギー保存の式からも求めることができます。
式は、「静止時のAの力学的エネルギ-の和」=「距離L移動した瞬間のAの力学的エネルギーの和」と表すことにします。
また、重力による位置エネルギーの基準を、「距離L移動したAの位置」にとります。すると
\begin{eqnarray} \frac{1}{2}m\times 0^2+mgL\sin\theta&=&\frac{1}{2}mv'^2+mg\times 0 \\
mgL\sin\theta&=&\frac{1}{2}mv'^2 　\\
v'&=&\sqrt{2gL\sin\theta}
\end{eqnarray}
（4）式と同じ結果が得られました。

２．自由に動く斜面上の物体の運動

　次に、斜面台が床から切り離され、自由に動く場合について考えてみます。
床と斜面台の間には摩擦はありません。　
右下図では、摩擦がないことを、斜面台に取り付けた車輪で表しています。

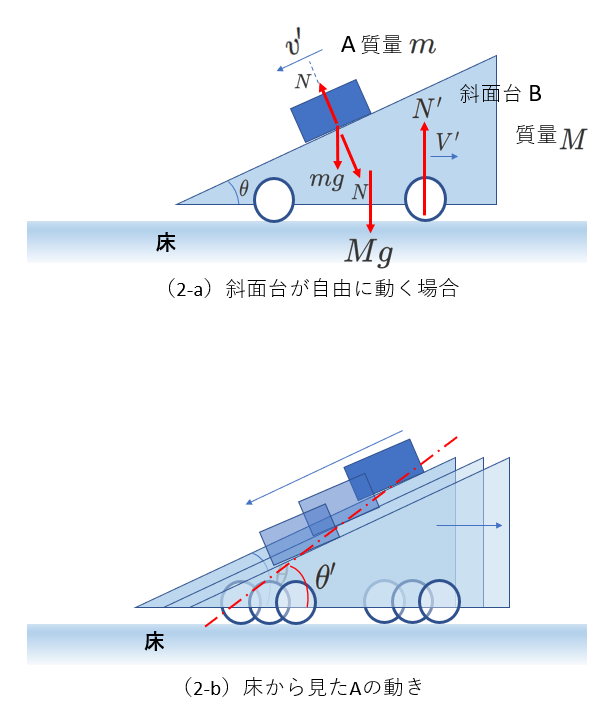
自由に動く斜面上の物体の運動

　物体Aと斜面台Bはどんな動きをするでしょうか。
Aは斜面に沿って下ります。
このとき、Bは、Aから抗力を受けて右向きに動きます。

　これらの動きを図に表したのが（2-b）です。

床から見たとき、Aは赤色の一点鎖線のように動きます。
水平方向との角度を\(\theta'\)と表すと、\(\theta'>\theta\)です。
つまり、図（1-b）に表した力の関係は成立しません。

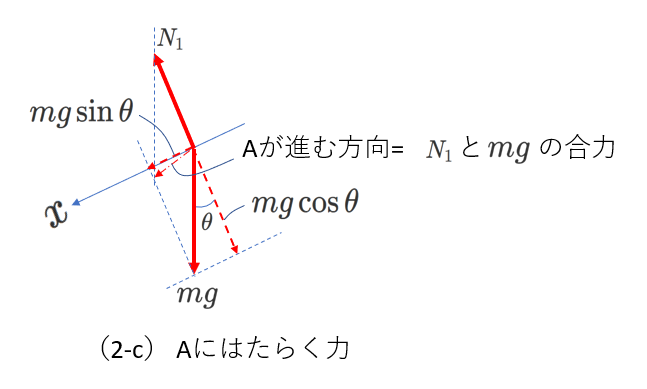
自由に動く斜面上の物体の運動#2

　図（1-b）との違いを、図（2-c）で確認してください。

　Aが進む向きは図（1-b）の\(x\)軸の方向から少しずれています。
この場合にも、
\(N_1\)と\(mg\) の合力の向きが、Aが進む向きになります。

　さて、物体Aと斜面台Bの運動方程式をどのように立てればよいでしょうか。

　まず、軸ですが、
\(\theta'\)がわかっていないこと、
斜面台Bは水平方向に動き、
　　　　　　　　　鉛直方向には動かないことから、
図（2-d）にように、\(x\)軸、\(y\)軸を設定します。

すなわち、水平方向が\(x\)軸、鉛直方向が\(y\) 軸です。

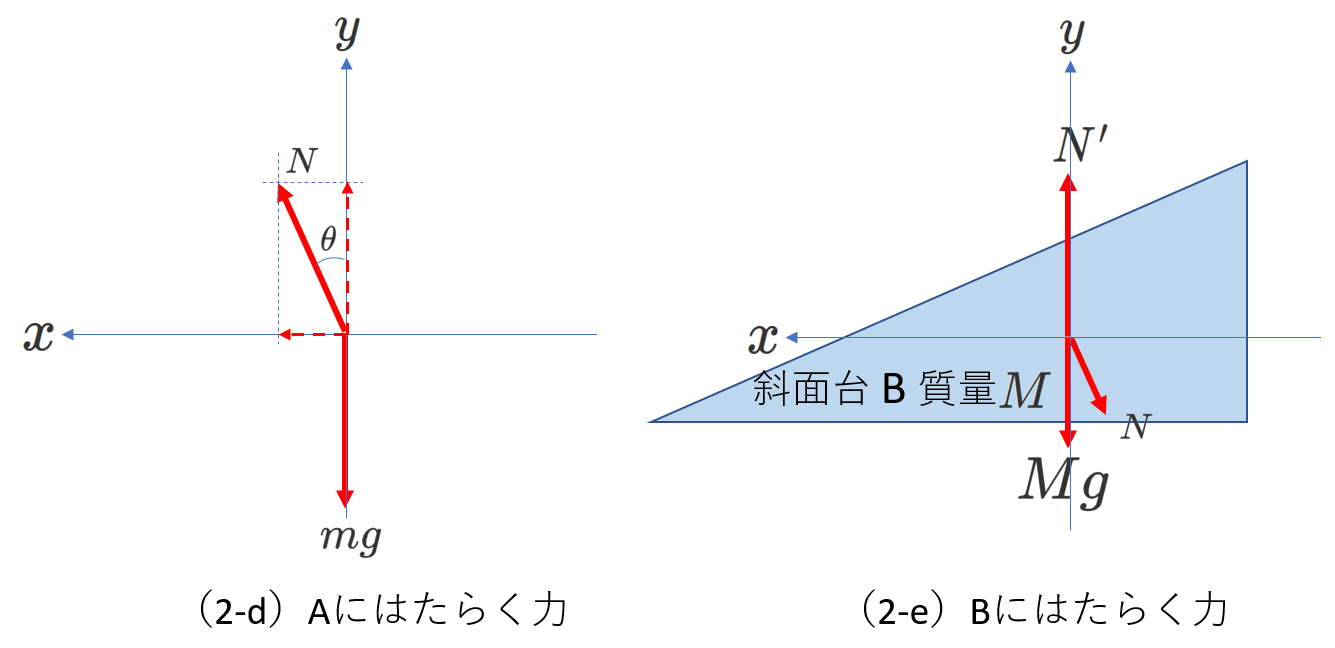
自由に動く斜面上の物体の運動#2

　では、運動方程式を立ててみます。
　物体Aの加速度の\(x\)成分を\(\alpha_x\)、\(y\)成分を\(\alpha_y\)、
斜面台Bの加速度の\(x\)成分を\(\beta_x\)、\(y\)成分を\(\beta_y\)、　（ただし、\(\beta_y=0\)です）
加速度の正の向きを、それぞれの軸の正の向きとします。

　図（2-d）を参照して、
　物体Aの水平方向（\(x\)軸方向）、および、鉛直方向（\(y\)軸方向）の運動方程式は
\begin{eqnarray} m\alpha_x&=&N\sin\theta \tag{5-5} \\
m\alpha_y&=&N\cos\theta-mg \tag{5-6}
\end{eqnarray}

斜面台Bの水平方向（\(x\)軸方向）、および、鉛直方向（\(y\)軸方向）の運動方程式は
\begin{eqnarray} M\beta_x&=&-N\sin\theta \tag{5-7} \\
m\times 0&=&N'-N\cos\theta-Mg \tag{5-8}
\end{eqnarray}
となります。
（5-8）式は、つり合いの式ともみなせて、変形すれば、\(N'=N\cos\theta+Mg \tag{5-8'} \) と書けます。

　未知数は、\(\alpha_x\)、\(\alpha_y\)、\(\beta_x\)、\(N\)の４つですから、方程式がひとつ足りません。
それには、物体Aが斜面を下るという条件を式に表します。
斜面台に居る観察者から物体Aを見れば、Aは角度\(\theta\)の斜面を下っているように見えることを式に表します。
これには、物体Aと斜面台Bとの相対加速度を考えればよいということですから、
\begin{eqnarray} \tan\theta&=&\frac{|\alpha_y|}{|\alpha_x-\beta_x|}=\frac{-\alpha_y}{\alpha_x-\beta_x}　\tag{5-9}　　\\
ここで、運動を考察することから、&&\alpha_y\lt 0 \\
&&\alpha_x-\beta_x\gt 0　、であることを用いました
\end{eqnarray}

　さて、（5-5）（5-6）（5-7）（5-9）式から、\(\alpha_x,\alpha_y,\beta_x,N\)を求めます。
（5-5）（5-6）（5-7）式を見ると、\(\alpha_x,\alpha_y,\beta_x\)が\(N\)で表されているので、
（5-5）（5-6）（5-7）式を（5-9）式に代入すれば、ただちに\(N\)が求まります。
\(N\)の値を（5-5）（5-6）（5-7）式に代入すれば、すべての未知数が求まります。

　そのようにして、求めた結果は、
\begin{eqnarray} N&=&\frac{mMg\cos\theta}{M+m\sin^2\theta} \tag{5-10} \\
\alpha_x&=&\frac{Mg\sin\theta \cos\theta}{M+m\sin^2\theta} \tag{5-11} \\
\alpha_y&=&-\frac{(M+m)g\sin^2\theta}{M+m\sin^2\theta} \tag{5-12} \\
\beta_x&=&-\frac{mg\sin\theta \cos\theta}{M+m\sin^2\theta} \tag{5-13}
\end{eqnarray}
です。

　検証しておきます。
　\(0<\theta<\frac{\pi}{2}\)ですから、\(\sin\theta>0\)、\(\cos\theta>0\)となり、
\(\alpha_x>0\)、\(\alpha_y<0\)、\(\beta_x<0\)です。
すなわち、Aは左下向きに動き、斜面台Bは右向きに動くこととなり、予想される動きと一致します。

　さて、上の結果から、斜面台が固定された場合の物体Aの加速度の（5-2）式を導くことができることを示します。
　斜面台の質量\(M\)を大きくしていくと、斜面台は動きにくくなります。
そこで、\(M\to\infty\)の極限を考えることで、斜面台Bが固定されているという状況を作ります。

　このとき結果の式は、
\begin{eqnarray} N&=&\frac{mMg\cos\theta}{M+m\sin^2\theta} =\frac{mg\cos\theta}{1+\frac{m}{M}\sin^2\theta} \to mg\cos\theta \tag{5-14} \\
\alpha_x&=&\frac{Mg\sin\theta \cos\theta}{M+m\sin^2\theta}=\frac{g\sin\theta \cos\theta}{1+\frac{m}{M}\sin^2\theta} \to g\sin\theta \cos\theta \tag{5-15} \\
\alpha_y&=&-\frac{(M+m)g\sin^2\theta}{M+m\sin^2\theta} =-\frac{(1+\frac{m}{M})g\sin^2\theta}{1+\frac{m}{M}\sin^2\theta} \to -g\sin^2\theta \tag{5-16} \\
\beta_x&=&-\frac{mg\sin\theta \cos\theta}{M+m\sin^2\theta} \to 0　\tag{5-17} \\
\\
これより、\\
\alpha&=&\sqrt{\alpha_x^2+\alpha_y^2}=g\sqrt{\sin^2\theta \cos^2\theta+\sin^2\theta \sin^2\theta}=g\sin\theta \ \ \ \ \ (\sin\theta>0) \tag{5-18} \\
\\
また、\tan\theta'&=&\frac{-\alpha_y}{\alpha_x-\beta_x}=\frac{g\sin^2\theta}{g\sin\theta\cos\theta-0}=\tan\theta \\
したがって、\theta'&=&\theta
\end{eqnarray}

　（5-18）式が（5-2）式と一致しました。

　(5-14)式から、斜面台が固定されている場合と、固定されていない場合とで、
垂直抗力の大きさが異なることを確認してください。

物理の大学入試問題を解く