物理の大学入試問題を解く

トップページ ＞ 力学 ＞ 張力

　糸の両端に物体AとBがつながれていて、糸がぴんと張っているとき、
AとBは糸から同じ大きさの張力を受けます。
ここでは、糸の両端で張力が同じ大きさとなる根拠を考えます。

 

　糸が静止している場合と、運動している場合で
議論が異なるので、二つに分けて考えます。

 

１．糸が静止している場合

 

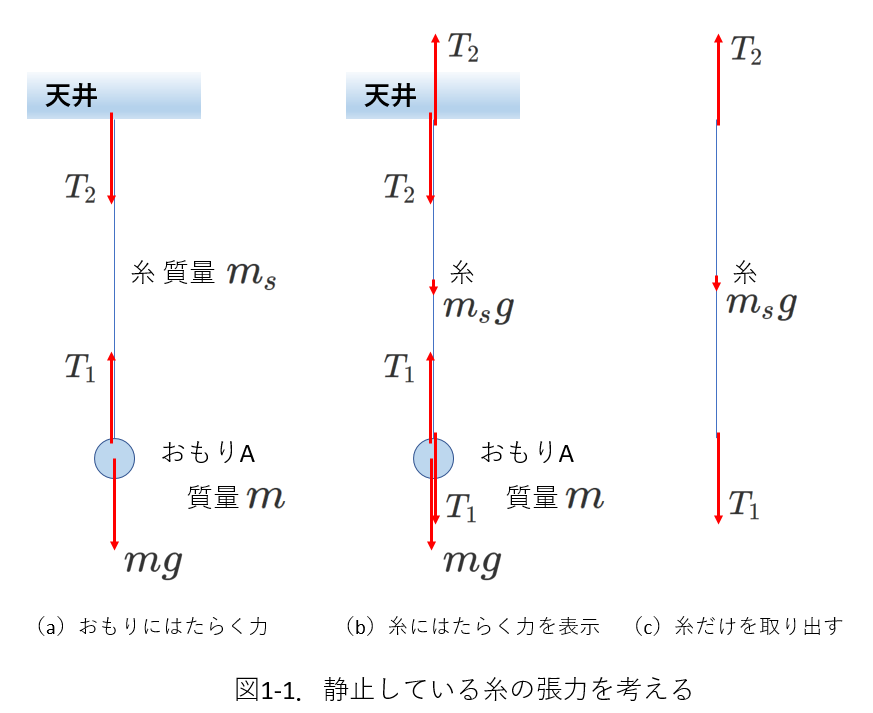
　図1-1に示すように、おもりA（質量\(m\)）を糸で天井から吊るします。
力がつりあって静止している場合を考えましょう。

 

　（a）に示すように、おもりAは糸から上向きの張力\(T_1\)と下向きの重力\(mg\)を受けます。
天井は、糸から下向きの張力\(T_2\)を受けます。

 

注1）\(T_1=T_2\)であることを以下で示すまでは、\(T_1とT_2\)と表します。
注2）天井には\(T_2\)とつりあう上向きの力もかかっているはずですが、省略します。

 

　問題では、おもりAに注目するので、
力の図を描く場合には（a）のように、おもりにはたらく力をすべて数え上げる一方で、
糸にはたらく力は無視することが普通です。

 

 

　今、敢えて糸にはたらく力を描くと、（b）のようになります。
ここで、糸の質量を\(m_s\)として、糸には\(m_sg\)の大きさの重力がはたらくとしています。

 

　接触している物体と物体（ここでは、おもりAと糸、糸と天井）は力を及ぼし合い、作用・反作用の法則が成り立つので、
糸は、おもりから下向きの大きさ\(T_1\)の力を、天井から上向きの大きさ\(T_2\)の力を受けます。

 

　今、糸について着目しているので、糸の部分だけ切り出せば（c）のようになります。

 

　さて、糸は静止しているので、3つの力（\(T_とT_2とm_sg\)）はつりあっています。
したがって、\(T_1+m_sg=T_2\)です。
　多くの問題では、「糸の質量は無視して良い」とか「糸の質量を\(0\)と考えて良い」などの
条件が付きます。つまり\(m_sg=0\)としてよいということなので、
\(T_1=T_2\)が得られます。

 

 

２．糸が等加速度運動をしている場合

 

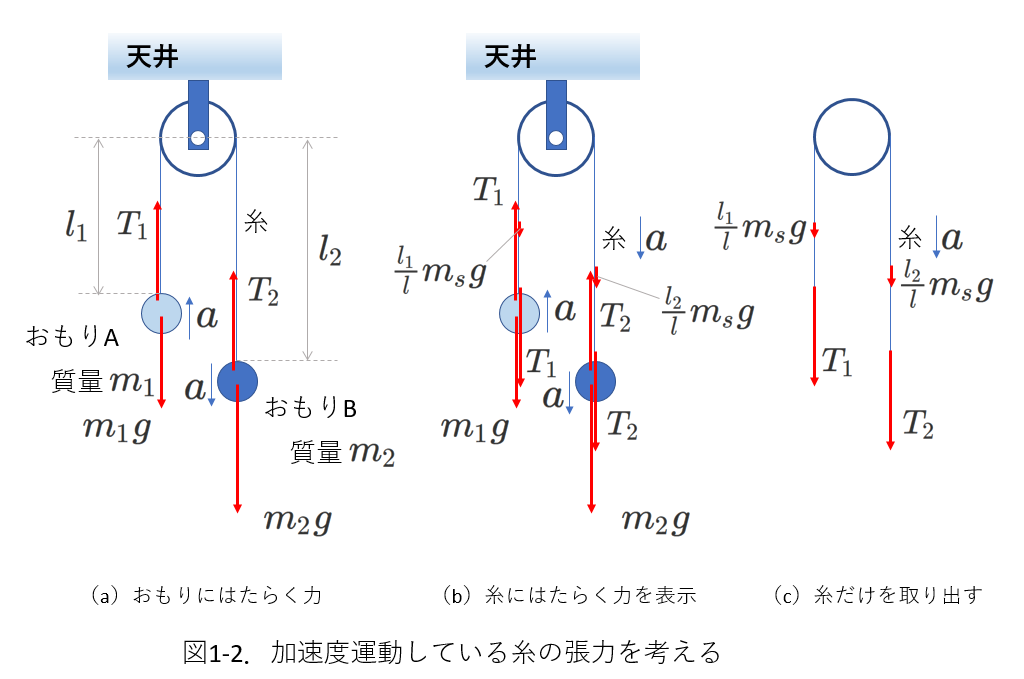
　糸が等加速度運動をしている場合にも、糸の両端で張力が同じ大きさと考えてよいことを示します。

 

　下図に示すように、天井に取り付けた滑車に糸を通し、糸の一方に質量\(m_1\)のおもりAを
他方に質量\(m_2(>m_1)\)のおもりBを取り付けます。

 

　ふたつのおもりは最初固定されています。
固定を外せば、糸がぴんと張られている状態で、おもりBは鉛直下向きに、おもりAは上向きに加速されます。
このとき、おもりAもBも糸も同じ大きさの加速度を持ちます。

 

　この加速度の大きさを\(a\)として、
おもりA、おもりB、糸の運動方程式を立ててみましょう。
ここで、糸の質量を\(m_s\)、糸の長さを\(l\)として、
時刻\(t\)には、滑車の左側の糸の長さが\(l_1\)、右側の糸の長さが\(l_2\)であったとすると、
左側の糸には\(\frac{l_1}{l}m_sg\)、右側の糸には\(\frac{l_2}{l}m_sg\)の大きさの重力が下向きにはたらきます。、

 

 

　おもりと糸の進む方向を加速度の正の向きとして、運動方程式は、
\begin{eqnarray} おもりA&：&m_1a=T_1-m_1g \tag{1-1} \\
おもりB&：&m_2a=m_2g-T_2 \tag{1-2} \\
糸&：&m_sa=T_2+\frac{l_2}{l}m_sg-T_1-\frac{l_1}{l}m_sg \tag{1-3} \end{eqnarray}

 

　一般的な問題では糸の運動方程式を立てる必要はありません。
そして、多くの問題では、
　「糸の質量は無視して良い」とか「糸の質量を\(0\)と考えて良い」などの
条件が付きます。つまり\(m_s=0\)としてよいということなので、（1-3）式を書き改めると、
\begin{equation} 0\times a=T_2-T_1 \tag{1-3'} \end{equation}

 

　\(a\)は題意から有限の値を持ちます。したがって、（1-3'）式の左辺は\(0\)ですから、\(T_1=T_2\)が得られます。
\(T_1=T_2\)では、糸は静止するのではないかと考えてしまいますが、
（1-3'）式は、\(0\times a=0\)となり、\(a\)がいくつであってもこの式は成り立ちます。
つまり、\(a\)は、（1-3）式からは決められず、（1-1）式（1-2）式から決まることになります。

 

　このように、糸の運動方程式は、糸の質量を無視できるという条件では、立式しても意味がありません。
そして、このときには\(T_1=T_2\)となり、糸の両端の張力は等しいと言えます。

 

 

 

３．【まとめ】
　まとめると、

 

３-1．　上のまとめの最後の文について考えます。

 

　図1-1（c）の図をもとに、右下に図1-3を描きました。
ここでは、\(m_s=0\)として、\(m_sg\)を省略し、\(T_1=T_2=T\)としています。

 

　さて、（c'）では1本に見える糸ですが、2本の糸（(d)で、糸1と糸2）がつながっているとして、
糸1と糸2が接続する部分にはたらく力を考えてみましょう。

 

 

考え方1：
　上の「まとめ」のとおり、糸の両端で張力の大きさは同じですから、
（e）のように、糸1の両端に大きさ\(T\)の張力が、糸2の両端にも大きさ\(T\)の張力がはたらきます。
糸1と糸2の接続部での張力は、糸1と糸2で向きが異なるので、力のつりあいを壊すことはありません。

 

考え方2：
　糸1も糸2も静止しているので、それぞれの糸にはたらく力はつりあっているはずです。
糸1だけ取り出して力のつり合いを考えると、接続部で下向きの大きさ\(T\)の力がはたらいているはずです。

 

　以上の考えから、図1-3（e）が妥当であると考えることができます。

 

 

 

 

3-2．　もうひとつの例を挙げます

 

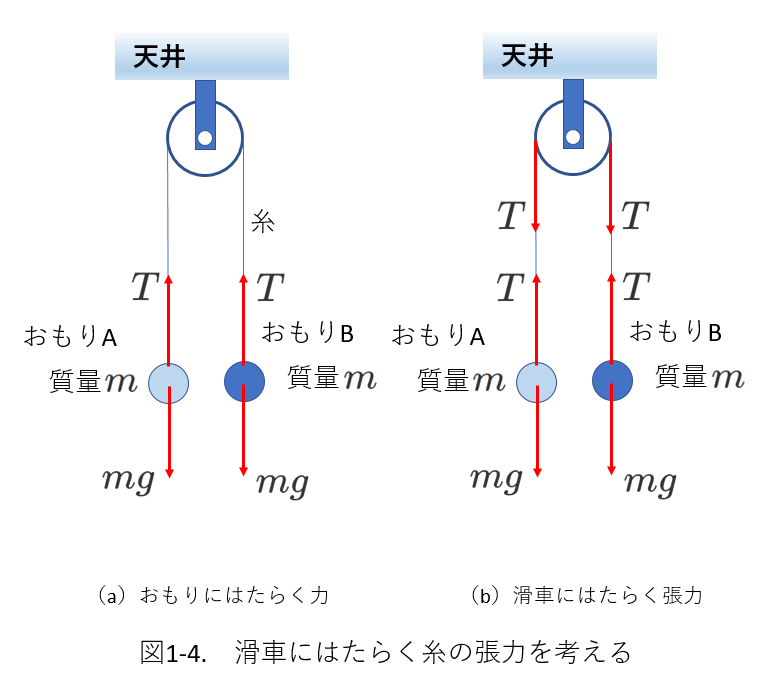
　右の図1-4のように、天井に固定した滑車に糸を通して両端に同じ質量\(m\)のおもりAとBをつなぎます。
ふたつのおもりにはたらく重力の大きさは等しいので、おもりは静止します。

 

　（a）のように、おもりにはたらく重力\(mg\)と糸の張力\(T\)のつり合いを考えると、\(T=mg\)です。

 

　ここで、糸が滑車に及ぼす力の大きさを考えます。

 

（b）のように、
　糸と滑車が接触（接続）するところには、力（この場合、張力）がはたらきます。
糸の両端で張力の大きさは同じ、なので、
糸が滑車に及ぼす力は、\(2T=2mg\)となります。

 

　なお、滑車は天井から大きさ\(2mg\)の上向きの力を受けて、静止しているわけですが、図ではこの力を省略しています。

 

　また、滑車は質量\(m\)のふたつのおもりをぶら下げているので、\(2mg\)の力を受けることになりますが、
おもりが直接に滑車に力を及ぼすわけではなく、
（b）のように、滑車は接触している糸から力を受けることになります。

 

 

 

　糸とおもりからなる系で、糸がぴんと張った状態で静止していれば、
力のつりあいから糸の張力を求めます。

 

【例1】　滑車の問題

 

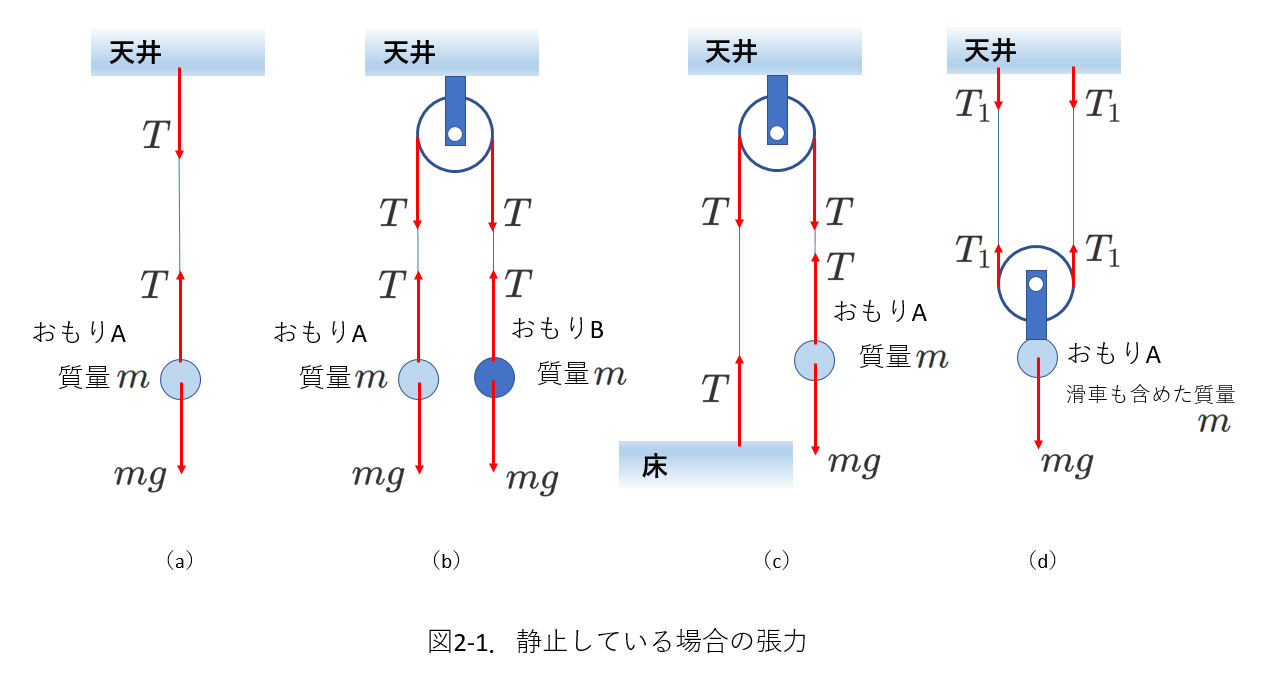
　図2-1に張力を求める4つの例題を挙げました。
いずれも糸の質量を無視できるとします。

 

①　最初に、力を図示します。　
　　おもりには重力がはたらきます。
　　糸の張力を\(T\)、または、\(T_1\)などとして、図中に描き入れます。
　　その際には、

　　を、参考にします。
　　図2-1には、このようにして描いた力を図示しました。
　　これらの図には、糸にはたらく力は図示されていません。

 

　

 

②　おもりが静止していることから、おもりにはたらく力のつりあいを考えます。
　　これにより、張力の大きさが求められます。
　　（a）（b）（c）では、おもりAにはたらく力のつりあいから、\(T=mg\)です。
　　（d）では、おもりと動滑車を含めた質量\(m\)にはたらく力のつりあいから、
　　\(2T_1=mg\)、したがって、\(T_1=\frac{1}{2}mg\)です。

 

③　図2-1を見れば、糸が滑車や天井や床におよぼす力が求められます。

 

 

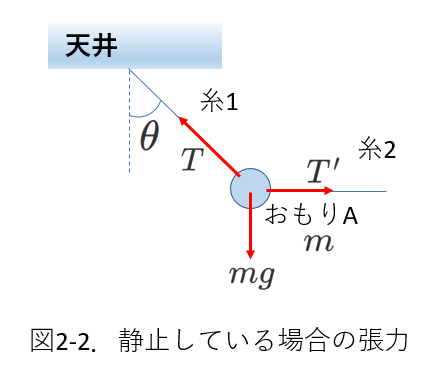
【例２】　糸が鉛直方向から傾いている場合

 

　右の図2-2では、天井から糸1で吊るされたおもりAが、
水平方向に糸2で引っ張られ、
糸1が鉛直から角度\(\theta\)だけ傾いて静止しています。
このときの糸1の張力\(T\)と糸2の張力\(T'\)を求めます。

 

　静止しているので力のつりあいを考えます。
①おもりAにはたらく力を図示すると右図のようになります。
　力は3つです。

 

②次におもりにはたらく力のつりあいを考えます。
　【例1】の場合と異なり、力は鉛直面内でつりあっています。
　したがって、2次元の力のつりあいを考えます。
ここでは、力の鉛直方向成分のつりあいと、水平方向成分のつりあいを考えます。

 

　すると、
\begin{eqnarray}　鉛直方向成分のつりあい&：& T\cos\theta=mg \\
　水平方向性分のつりあい&：&T\sin\theta=T' \\
　したがって、T&=&\frac{mg}{\cos\theta} \\
T'&=&\frac{mg\sin\theta}{\cos\theta}=mg\tan{\theta}
\end{eqnarray}

 

 

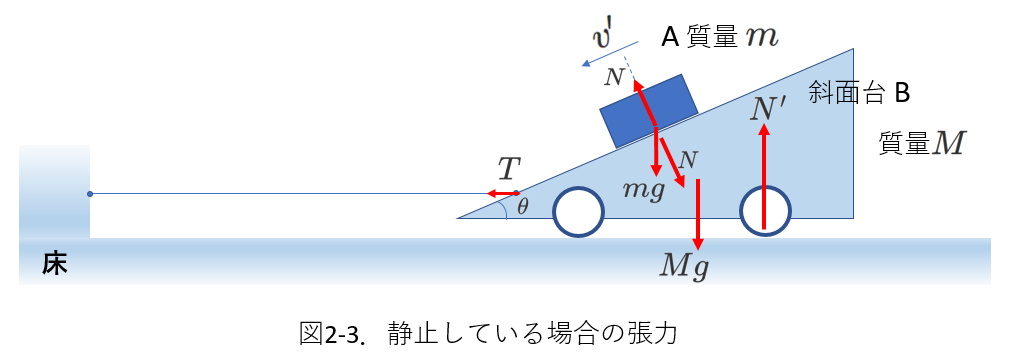
【例3】 斜面台につないだ糸の張力

 

 

図2-3に示すように、
斜面台Bの上で物体Aが斜面を滑り降りています。
斜面台Bと床の間にも、物体Aと斜面台Bの間にも摩擦ははたらいていません。
斜面台は糸で壁につながれています。

 

　斜面台Bは物体Aの垂直抗力で右向きに押されていますが、
糸があるために、右に動き出すことはなく、静止しています。

 

　このとき、糸が斜面台に及ぼす張力\(T\)を求めてみます。

 

①斜面台と物体Aにはたらく力を図示すると、図2-3のようになります。
斜面台Bには、
　Aからの垂直抗力\(N\)
　糸からの張力\(T\)
　重力\(Mg\)
　床からの垂直抗力\(N'\)
の力がはたらきます。

 

　斜面台自身は静止しているので、力はつりあっているはずです。
力の向きは2次元的なので、水平方向成分と鉛直方向成分のそれぞれについての力のつりあいを考えます。
\begin{eqnarray}
水平方向成分&：&T=N\sin\theta \tag{2-1} \\
鉛直方向成分&：&N'=Mg+N\cos\theta \tag{2-2}
\end{eqnarray}

 

　（2-1）式のNを求めるには、物体Aの運動を考えます。
物体Aは斜面を滑り降りています。斜面台は静止しています。
このとき、斜面に垂直な方向には動いていないので、
物体にはたらく垂直抗力\(N\)と重力\(mg\)の斜面に垂直な方向の成分はつりあっています。
　すなわち、\(N=mg\cos\theta\) です。（\(N\)が一定であることにも注意してください。）
この式と（2-1）式から\(T\)を求めることができます。

 

 

 

 

【例4】　可動台につないだ糸の張力

 

　図2-4に示すように断面が半円の台Bの上で、この断面内で物体Aは運動してします。
今、(a)に示すように、半円の最下端で静止しているAに、初速\(v_o\)を右向きに与えます。
Bの内面(半円）に沿って、Aは動きます。
半円の中心とAを結ぶ線分と鉛直との角度が\(\theta\)のとき、Aの速さを\(v\)として、
糸がBに及ぼす張力\(T\)を求めます。

 

　AおよびBにはたらく力は図2-4（b）に示す通りです。

 

　さて、これは鉛直面の円運動と考えられます。
Aにはたらく垂直抗力はAに対して仕事をしないこと、重力は保存力であることから、
物体Aについて力学的エネルギー保存則が成り立ちます。

 

　解法の手順は、
①力学的エネルギー保存則から\(v\)を求める。
②おもりAについて運動方程式を立て、垂直抗力\(N\)を求める。
③Bに対する力のつりあいから、\(T\)を求める。

 

①力学的エネルギー保存則は、(a)初期状態のAの位置を基準として、
\begin{equation} 　\frac{1}{2}mv_o^2+mg\times 0=\frac{1}{2}mv^2+mgr(1-\cos\theta) \tag{2-3} \end{equation}
これより、
\begin{equation} 　v=\sqrt{v_o^2-2gr(1-\cos\theta)} \tag{2-4} \end{equation}

 

②Aについての運動方程式は、
\begin{eqnarray} 　m\frac{v^2}{r}=N-mg\cos\theta \tag{2-5} \\
N=m\frac{v^2}{r}+mg\cos\theta \tag{2-6}
\end{eqnarray}

 

③Bにはたらく力の水平方向成分のつり合いを考えて、
\begin{equation} 　T=N\sin\theta \tag{2-7} \end{equation}

 

　（2-7）（2-6）（2-4）式を用いて\(T\)を計算できます。

　糸と物体からなる系で、糸がぴんと張った状態で運動していれば、
物体についての張力を含む運動方程式を立てて、張力を求めます。
このとき、物体の加速度と張力が未知数になるので、
複数の運動方程式を立てるか、それに代わる別の条件が必要になります。

 

 

 

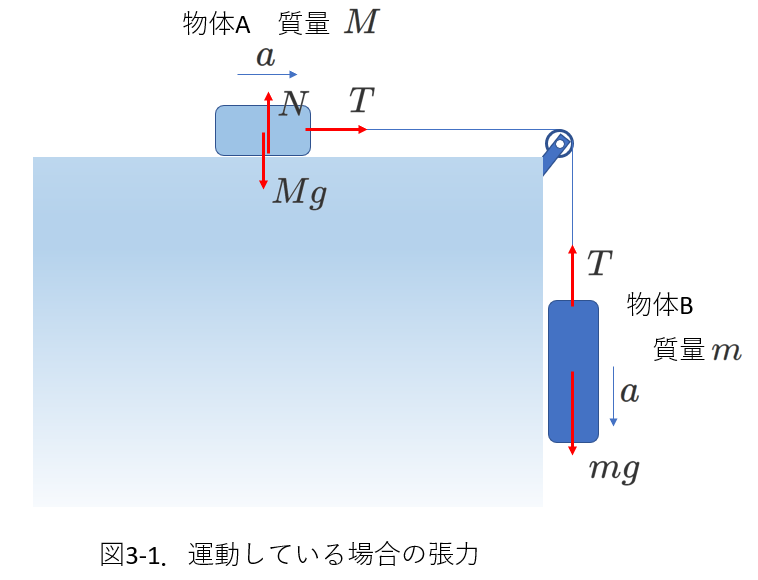
【例１】
　右の図3-1の状態の糸の張力を考えます。

 

　質量\(M\)の物体Aがテーブル上の水平面に置かれています。
Aは糸につながれ、糸のもう一方の端は、テーブルの角に設けられた滑車を通して、質量\(m\)の物体Bをつりさげています。

 

　物体Bは重力により下向きに、Aは糸に引かれて右向きに加速します。

 

　Aとテーブルの表面の間には摩擦はなく、
糸がぴんと張った状態で運動が継続し、
糸の質量は無視でき、糸は伸び縮みしないものとします。

 

 

①最初に、物体AとBにはたらく力を図示します。
　AとBには重力(大きさはそれぞれ\(Mg,mg\)）がはたらきます。
　Aはテーブル上に置かれているので垂直抗力\(N\)を受けます。

 

　また、糸の張力がはたらきます。張力は、

　ですから、張力の大きさを\(T\)として図示すれば、図3-1の赤矢印のようになります。

 

　注）糸にはたらく力を考える必要はありません。
　　　質量が\(0\)とされる糸について運動方程式を立てる意味がないからです。

 

 

②次に、物体AとBについて運動方程式を立てます。

 

　　物体Aは水平右向きに動きます。
　これに垂直な鉛直方向には動きません。（加速されません。）
　つまり、鉛直方向の力はつりあっているはずですから、直ちに、\(N=Mg\)が得られます。

 

　物体Bは鉛直下向きに動き（加速）します。
　そして、糸は伸び縮みしないので、AとBの加速度の大きさは等しいはずです。
　加速度の大きさを\(a\)とします。

 

　この「AとBの加速度が等しく、AとBについてふたつの運動方程式を立式できる」というのが、解法のポイントです。

 

　運動方程式を立てるにあたって、物体AとBの進む向きを、加速度と力の正の向きとします。
　つまり、物体Aは水平右向きが正の向き、
　物体Bは鉛直下向きが正の向きです。

 

　運動方程式は、
\begin{eqnarray} 物体A&：&Ma=T　　\tag{3-1} \\
　物体B&：&ma=mg-T \tag{3-2}
\end{eqnarray}
となります。

 

　未知数は、\(aとT\)のふたつで方程式もふたつですから、、\(aとT\)を求めることができます。

 

　（3-1）式と（3-2）式の両辺同士を足し合わせれば、
\begin{eqnarray}　　Ma+ma=mg、　
&a&=\frac{mg}{M+m} 　\tag{3-3} \\
　これを、（3-1）式に代入して、
　T&=&\frac{Mmg}{M+m} \tag{3-4}
\end{eqnarray}

 

　（3-3）（3-4）式からわかるように、\(aもT\)も定数です。
したがって、この運動は等加速度運動です。

 

 

 

 

 

 

 

 

 

 

 

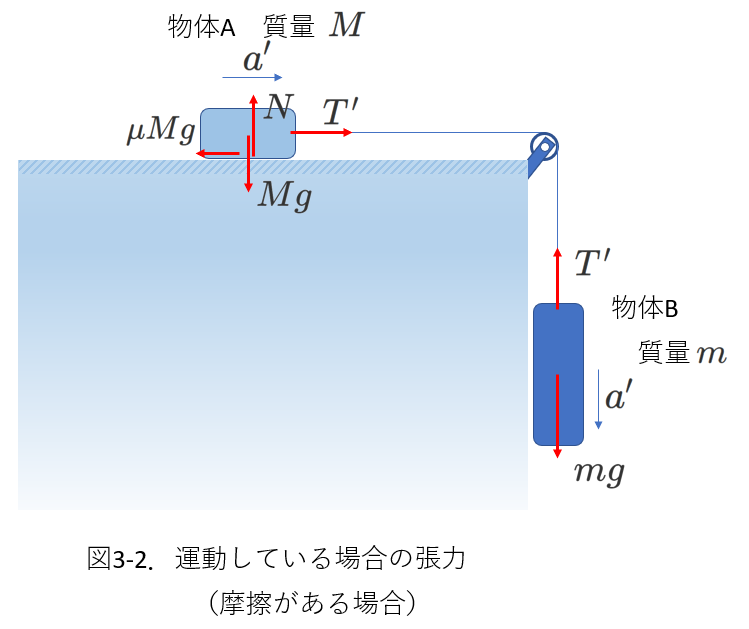
【例2】

　[例1]において、物体Ａとテーブルの水平面との間に摩擦がある場合について考えます。
　\(N=Mg\)ですから、動摩擦係数を\(\mu\)とすると、
摩擦力の大きさは\(\mu Mg\)で、
物体Aは右向きに動いているので、
摩擦力は左向きにはたらきます。

 

　物体A,Bの加速度を\(a'\)、張力を\(T'\)として、
運動方程式は、
\begin{eqnarray} 物体A&：&Ma'=T'-\mu Mg　　\tag{3-7} \\
　物体B&：&ma'=mg-T' \tag{3-8}
\end{eqnarray}
となります。

 

　（3-7）式と（3-8）式の両辺同士を足し合わせれば、
\begin{eqnarray}　　Ma'+ma'=mg-\mu Mg、　
&a'&=\frac{mg-\mu Mg}{M+m} 　\tag{3-9} \\
　これを、（3-7）式に代入して、
　T'&=&\frac{M(mg-\mu Mg)}{M+m}+\mu Mg \\
&=&\frac{Mmg(1+\mu)}{M+m} \tag{3-10}
\end{eqnarray}

 

 

 

 

 

 

【例3】

 

　図3-3では、滑車にかけた糸の片側に質量\(m_1\)のおもりAが、もう一方に質量\(m_2\)のおもりBがつながっています。
\(m_1\lt m_2\)であるため、ふたつのおもりは図3-3に示した向きに加速されます。

 

①最初におもりA,Bにはたらく力を図示すると、図3-3のようになります。

 

②次に、おもりAとBについて運動方程式を立てます。

 

　おもりの進む向きを加速度の正の向きとし、おもりの加速度を\(a\)として、おもりA,Bについて運動方程式を立てると、
\begin{eqnarray} おもりA&：&　m_1 a=T-m_1g \tag{3-15} \\
おもりB&：&　m_2 a=m_2g-T \tag{3-16}
\end{eqnarray}
となります。

 

　（3-15）式と(3-16)式の左辺、右辺同士を足し合わせると、
\begin{equation} (m_1+m_2)a=m_2g-m_1g \tag{3-17} \end{equation}
この式は、質量\(m_1\)と\(m_2\)のふたつのおもりを、重力\(m_2gとm_1g\)の差の力で加速し、
その加速度が\(a\)であることを意味しています。
これは、妥当な式です。

 

　これから、
\begin{eqnarray} a&=&\frac{(m_2-m_1)g}{m_1+m_2}　\tag{3-18} \\
T&=&\frac{2m_1m_2g}{m_1+m_2} \tag{3-19}
\end{eqnarray}
となります。

 

 

 

【例4】

 

 

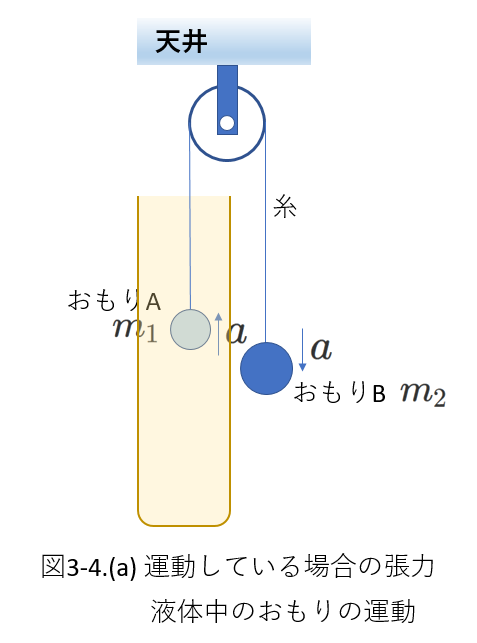
　次の例の図3-4（a）は、図3-3のおもりAを液体に浸した場合です。
液体に浸したおもりAには新たにふたつの力が加わります。

 

 

　ひとつめは浮力です。

 

　物体の浮力の大きさは、その物体がおしのける液体の質量にはたらく重力と等しいので、おもりAの体積を\(V\)、液体の密度を\(\rho\)とすると、
浮力の大きさは、\(\rho Vg\)です。

 

　ふたつめは液体の抵抗力です。
液体の中を\(v\)の速さで進むおもりには、\(v\)に比例した抵抗力がはたらきます。
ここで、比例定数を\(k\)とすると、抵抗力の大きさは\(kv\)、
向きはおもりの進む向きと逆の向きです。

 

　抵抗力は、その大きさが速さに比例するということで、ほかの重力や静電気力とは異なる出題のされかたをします。
　速度の大きさに比例し、その向きが速度の逆ということは、
加速されて、速度が増すと、抵抗力が大きくなり、加速度を低下させる、という変化になります。

 

つまり、加速度は一定ではなく時間がたつにつれて低下し、最終的には加速度は\(0\)、すなわち、速度は一定になります。
このため、「一定となったときの速さを求めよ」という出題がされます。
　そこで、ここでも、「一定となったときの速さ」を求めてみます。

 

速さに比例という意味では、ローンレンツ力も同じですが、その向きは異なります。（速度の逆向きではありません。）

 

さて、

ですから、AまたはBを使って問題を解くことになります。
以下では、最初にAで考え、次に、Bの考えを用いて、一定となったときの速さを求めてみます。

 

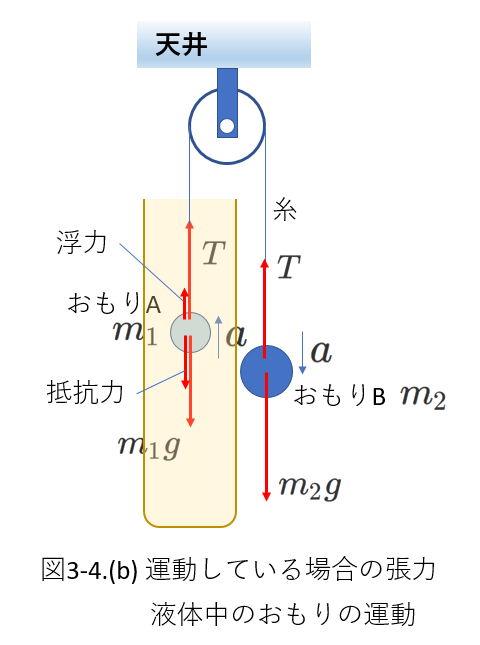
［例4］-1　
「A．加速度が\(0\)であること」を使って解きます。
運動方程式を立て、加速度を求め、
この式で加速度\(=0\)として、一定となった速さと張力を求めます。

 

①最初におもりA,Bにはたらく力を図示すると、図3-4（b）のようになります。

 

　おもりBにはたらく力は全部で4つです。
力を図示して、数え落としがないようにしましょう。

 

　重力がはたらくのは当然、
　おもりは糸に接触しているので、糸から張力を受けます
　おもりは液体に接触しているので、液体から浮力と抵抗力を受けます。
　　抵抗力を忘れやすいですが、
　　　問題では抵抗力の比例定数が示されるはずですから、
　　　問題文をしっかり読めば、抵抗力を数え落とすことはありません。

 

②次に、おもりAとBについて運動方程式を立てます。

 

時刻\(t\)で、おもりAとBの加速度は\(a\)、速度は\(v\)であったとします。
　（運動方程式を立てる場合、加速度を仮定して立式しますが、ここでは、
　速度まで仮定して運動方程式を立てることを覚えておきましょう。）
　おもりの進む向きを加速度の正の向きとし、おもりの加速度を\(a\)として、おもりA,Bについて運動方程式を立てると、
\begin{eqnarray} おもりA&：&　m_1 a=T+\rho Vg-m_1g-kv \tag{3-20} \\
おもりB&：&　m_2 a=m_2g-T \tag{3-21}
\end{eqnarray}
となります。

 

　上の式で、時間がたっても変化しない"定数"と、時間に伴って変化する変数とを区別することが大切です。
それをはっきりさせる形で式を書き直すと、
\begin{eqnarray} おもりA&：&　m_1 a(t)=T(t)+\rho Vg-m_1g-kv(t) \tag{3-20'} \\
おもりB&：&　m_2 a(t)=m_2g-T(t) \tag{3-21'}
\end{eqnarray}
　質量や重力加速度\(g\)は定数、密度\(\rho\)、体積\(V\)も定数ですから、重力\(m_1g\)、\(m_2g\)も定数、
浮力\(\rho Vg\)も定数となります。
加速度が0でないかぎり\(v\)は時間的に変化します。ですから、\(v\)は変数、
この故に、加速度\(a\)も、張力\(T\)も変数です。
例3では加速度は定数（等加速度運動）でした。
問題の構成を比較してみてください。

 

　一定と考えて式を変形すると思わぬミスをすることがあるので注意が必要です。
数学的には、（3-20’）（3-21’）が使われますが、物理は（3-20）（3-21）を使うことが多いです。

 

　さて、（3-20）（3-21）を解くと、
\begin{eqnarray}
a&=&\frac{\rho Vg+m_2g-m_1g-kv}{m_1+m_2} \tag{3-22} \\
T&=&m_2g-m_2a=\frac{m_2(2m_1g-\rho Vg+kv)}{m_1+m_2} \tag{3-23}
\end{eqnarray}
　\(\rho Vg=0、kv=0\)とすると、（3-18）（3-19）と同じになります。

 

　（3-22）式から、時間により\(a\)と\(v\)がどう変化するか考えてみましょう。
最初の\(v=0\)のときには、\(a\)は最大でおもりは加速され、\(v\)は増加します。
\(v\)が増加すれば\(a\)は小さくなり、さらに\(v\)が大きくなることで、\(a=0\)となります。
このとき、\(v\)は一定値となり、この状態が維持されます。

 

　そこで、（3-22）式で、\(a=0\)とし、このときの\(v\)の値を\(v_o\)とすると、
\begin{eqnarray} \rho Vg+m_2g-m_1g-kv_o=0 \\
ゆえに、v_o=\frac{ \rho Vg+m_2g-m_1g}{k} \tag{3-24}
\end{eqnarray}

 

 

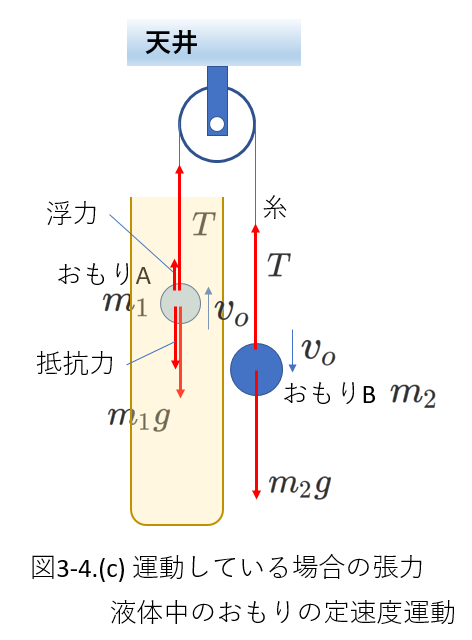
[例4]-2
　では、Bの考えで解いてみましょう。

 

 

　右の図3-4（c）に、速度が一定になったときの状態を図示してみました。
おもりAもBも一定の速度\(v_o\)で運動しています。
そこで、おもりAにはたらく力はつりあっていて、進む向きの力の和の大きさと逆向きの力の和の大きさは等しいという式を立てます。
おもりBについても同様に考えて、
\begin{eqnarray} T+\rho Vg&=&m_1g+kv_o　 \tag{3-25} \\
　m_2g&=&T \tag{3-26}
\end{eqnarray}
　\(v_o\)以外に\(T\)も未知数ですから、2つの方程式が必要です。

 

　また、おもりにはたらく力の合力は\(0\)と考えて式を立てると、
\begin{eqnarray} T+\rho Vg-m_1g-kv_o=0 \tag{3-27} \\
　m_2g-T=0 \tag{3-28}
\end{eqnarray}　
となります。
　これらの式は（3-25）（3-26）式と等価です。
また、これらの式は、（3-20）（3-21）式で、\(a=0\)としたときの式と等価です。

 

 

 

 

 

 

【例5】
　次の図3-5の場合を考えます。
動滑車をひとつ付け加えました。
この動滑車の質量は無視できるものとします。
　さて、

 

　ということですから、糸の張力を\(T\)として、ふたつのおもりに関係する場所に張力を記入すると、
図3-5のようになります。
おもりAには\(2T\)がはたらくことに注意しましょう。
　張力以外におもりには重力がはたらきます。
また、\(m_1\lt m_2\)とします。

 

　運動方程式を立てます。
この問題では、おもりAとBの加速度を同じと考えることはできないので、
おもりAの加速度を\(\alpha\)、Bの加速度を\(\beta\)とします。
おもりBが下降したとき、Aは上向きにうごきますから、
下向きを\(\beta\)の正、上向きを\(\alpha\)の正の向きとします。

 

　運動方程式は、
\begin{eqnarray}
おもりA&：&m_1\alpha=2T-m_1g \tag{3-29} \\
おもりB&：&m_2\beta=m_2g-T \tag{3-30}
\end{eqnarray}
となります。
　未知数は\(T、\alpha、\beta\)の3つですから、方程式がひとつ足りません。

 

 

注）今おもりAが\(a\)だけ上向きに変位したとします。
　　動滑車に左側の糸が長さ\(a\)だけあまり、右側の糸も\(a\)だけあまるので、
　　おもりBは\(2a\)だけ下向きに動くことになります。
　　図3-5（b）を参照してください。

 

　（3-31）式を（3-30）式に代入して、
\begin{eqnarray}
おもりA&：&m_1\alpha=2T-m_1g \tag{3-29'} \\
おもりB&：&2m_2\alpha=m_2g-T \tag{3-30'}
\end{eqnarray}

 

　これより、\(T=\frac{3m_1m_2g}{m_1+4m_2}\) です。

 

 

 

 

 

 

 

 

【例6】

　図3-6では、さらに、定滑車1個とおもりを1個増やしました。

 

　おもりが上下のどちらに動くかは、それぞれの質量の関係により、色々な場合がありそうです。
ここでは、おもりA、B、Cそれぞれの加速度を\(\alpha\)、\(\beta\)、\(\gamma\) として、図3-6に示した向きを加速度の正の向きと決めて、
立式してみました。

 

　それぞれのおもりにはたらく力は図3-6のとおりですから、運動方程式は、
\begin{eqnarray} おもりA&：&m_1\alpha=m_1g-T \tag{3-32} \\
　　おもりB&：&m_2\beta=2T-m_2g \tag{3-33} \\
　　おもりC&：&m_3\gamma=m_3g-T \tag{3-34}
\end{eqnarray}

 

\(\alpha、\beta、\gamma\)の間の関係は、
おもりAが下向きに\(a\)、おもりCが下向きに\(c\)変位したとき、おもりBは上向きにb変位するわけですから、\(a+c=2b\)です。
したがって、
\begin{equation} \alpha-2\beta+\gamma=0 \tag{3-35} \end{equation}

 

　（3-32）（3-33）（3-34）式から\(\alpha、\beta、\gamma\)を求め、（3-35）式に代入すると\(T\)が求められます。

 

　\begin{equation} T=\frac{4m_1m_2m_3g}{m_1m_2+m_2m_3+4m_1m_3} \tag{3-36} \end{equation}　
\(\alpha\)は、
　\begin{equation} \alpha=\frac{(m_1m_2-3m_2m_3+4m_1m_3)g}{m_1m_2+m_2m_3+4m_1m_3} \tag{3-37} \end{equation}　

 

つまり、\(m_1m_2-3m_2m_3+4m_1m_3\)が正のとき加速度は下向き、負のときは上向きとなります。

　これまでの張力の例題は、それぞれのおもりに重力が作用するものでした。
これは、質量を介して力がはたらくとも言えます。
しかし、ここではおもりに直接に力がはたらく場合について考えます。

 

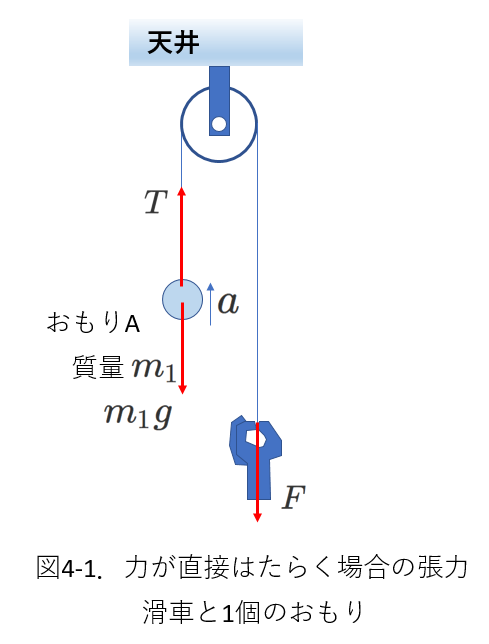
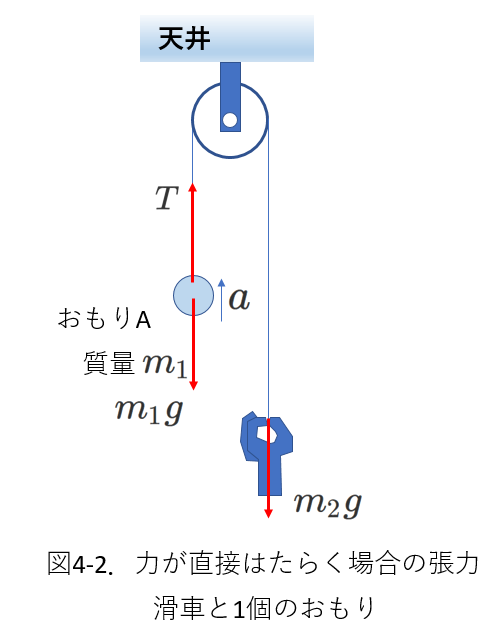
　ちょっと変わった例で、右の図4-1の場合を考えます。
　滑車に通した糸の一方に質量\(m_1\)のおもりAをつなげ、糸の他方を手でつかみ、大きさ\(F\)の力で下向きに引っ張ります。
このときの張力はいくつでしょうか。

 

　これは、力\(F\)でおもりAを引いていることになりますから、\(T=F\)となります。

 

　注意すべきは、\(F\)は糸にはたらいていることです。

 

　張力\(T\)は手が持つ糸の他端にもはたらくので、糸にはたらく力がつりあっていて、糸は静止（あるいは等速度運動）するように見えます。
しかし、「Ⅰ．糸の両端で張力の大きさは等しい」で説明したように、
糸の質量\(0\)の場合は、力がつりあっていても、加速度運動をする場合があります。
加速度運動なのか、等速度運動なのかは、質量をもったおもりの側の運動方程式で決まります。
それゆえ、糸に関する運動方程式を考える必要はありません。。

 

 

 

 

 

　それでは、右の図4-2の場合の張力\(T\)はいくつでしょう。
図4-2では、手が\(m_2g\)という力で糸を引いています。
つまり、質量\(m_2\)の物体にはたらく重力と同じ大きさの力で、手が引いたということです。
図4-1の例を考えれば、\(T=m_2g\)です。

 

　おもりAについて運動方程式を立てれば、
\begin{equation} m_1a=m_2g \tag{4-1} \end{equation}
となります。

 

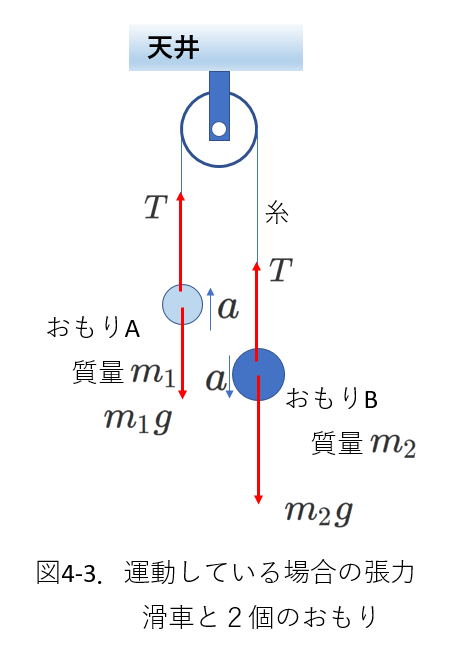
　この例と、右下の図4-3の例との違いを考えます。
図4-3は、「Ⅲ．運動している場合の張力」の【例3】、図3-3と同じ状況です。

 

 

 

 

 

　　

　既に【例3】で立式したように、
　おもりの進む向きを加速度の正の向きとし、おもりの加速度を\(a\)として、おもりA,Bについて運動方程式を立てると、
\begin{eqnarray} おもりA&：&　m_1 a=T-m_1g \tag{3-15} \\
おもりB&：&　m_2 a=m_2g-T \tag{3-16}
\end{eqnarray}
　これらの式の左辺、右辺同士を足し合わせると、
\begin{equation} (m_1+m_2)a=m_2g-m_1g \tag{3-17} \end{equation}

 

 

　（4-1）式と（3-17）式を比べると、図4-2と図4-3の違いがはっきりします。

 

　（4-1）式は、力\(m_2g\)で質量\(m_1\)を動かすことを意味しています。

 

　一方、（3-17）式は、質量\(m_1\)と\(m_2\)のふたつのおもりを、重力\(m_2gとm_1g\)の力の差で動かすことを意味しています。

 

　つまり、図4-3の場合のように、質量\(m_2\)が存在して、これに重力\(m_2g\)がはたらくという場合には、\(m_2g\)は（ほかの力とともに）\(m_2\)自身を含めた系全体にはたらきますが、
図4-2の場合、力の大きさが\(m_2g\)と言っても、質量\(m_2\)は存在しないので、おもりAだけにはたらくことになります。

　他端が固定された糸に結ばれたおもりが円運動をする場合の糸の張力を考えます。
ここでは、水平面内での円運動と鉛直面内での円運動に分けて張力を求めます。

 

１．水平面内で円運動している場合の張力

 

　図5-1に示すように、
一方の端が点Oに固定された糸のもう一方の端に結ばれたおもりAが、
点Oを中心にして水平に置かれたテーブル上で円運動をしています。

 

　Aの質量を\(m\)、円運動の半径は\(r\)、おもりの速さを\(v\)とします。

 

　おもりAには重力がはたらきますが、
その向きはテーブルに垂直で、テーブル面からの垂直抗力とつりあうため、
円運動には影響せず、図には示していません。

 

（1）テーブル上の人が円運動を観察した場合

 

　図5-1に示すように、おもりAは重力と垂直抗力以外に、
糸から張力を受けます。
　張力は、直線運動しようとするおもりAを常に円運動の中心の向きに
加速し、円運動を維持するようにはたらきます。

 

　円運動の運動方程式を立てると、
\begin{equation} m\frac{v^2}{r}=T \tag{5-1} \end{equation}
つまり、\(T=m\frac{v^2}{r}\)です。

 

　この式は、テーブル上にいる人間が観察している場合の式です。
この人には、おもりが常にその運動の向きを変えているように見えるので、
おもりを円運動の中心に向ける力（糸の張力）がはたらいている、と理解するわけです。

 

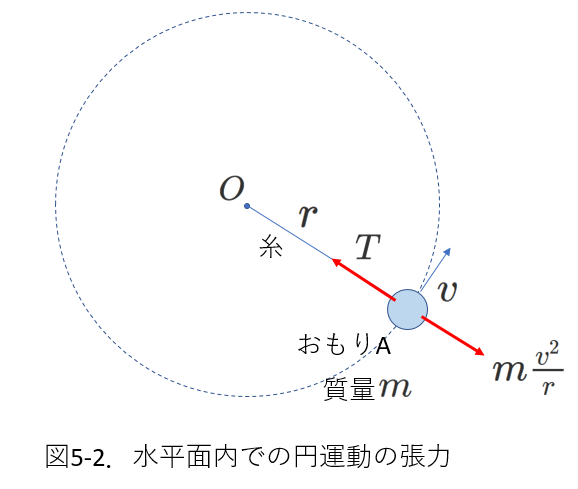
（2）おもり上の人が円運動を観察した場合

 

　この場合、おもりと一緒に運動しながらおもりを観察しているので、
等速度運動、あるいは、静止しているように感じます。

 

　糸に引っ張られているはずなのに、その向きに動いて行かないことから、
糸の張力につりあう別の力が逆向きにはたらいていると推察できます。

 

　それが、遠心力で、その大きさは、\(m\frac{v^2}{r}\)で表されます。
これは、（5-1）式の円運動の運動方程式の左辺と同じ式です。

 

　そのようすを、図に表すと、図5-2のようになります。
おもり上の人の目からは、おもりは等速度運動、あるいは、静止しているわけですから、張力と遠心力がつりあっていると考えます。

 

　それを式に表すと、
\begin{equation} T=m\frac{v^2}{r} \tag{5-2} \end{equation}
となります。

 

　（5-2）式は（5-1）式とまったく同じですが、立式の根拠となる考えは異なります。

 

 

 

 

２．鉛直面内で円運動している場合の張力

 

　次の例は、鉛直面内で円運動をしている場合です。

 

　図5-3では、糸の一端を点Oに固定し、他端をおもりAに結びます。
糸をぴんとはった状態で糸が水平になるようにおもりAを持ち上げ、鉛直下向きに初速\(v_o\)を与えます。（図5-3(a)）
この運動のすべては、ひとつの鉛直面内で起こるものとします。

 

　この場合、おもりは点Oを中心とした円運動をしますが、図5-1の場合とは異なり、
おもりにはたらく重力はおもりに対して仕事をするために、
おもりの位置により、おもりの速さが異なります。
したがって、おもりの速さも未知数として出題されることが多いです。
（図5-1では、一定の速さで円運動をします。）

 

 

　①力学定エネルギー保存則
　さて、この運動でおもりAの力学的エネルギーが保存されると考えてよいでしょうか。
おもりにはたらく力は重力と糸の張力です。
このうち、重力は保存力ですが、張力は保存力ではありません。
（保存力だけであれば、力学的エネルギーは保存されます。）

 

　張力は保存力ではありませんが、
図5-3からもわかるように、
糸の張力は、つねにおもりの進む方向に対して垂直の向きにはたらいています。
つまり、糸の張力は、おもりにたいして仕事をしていません。

 

　仕事をしていないということは、おもりの力学的エネルギーを増やしも減らしもしない、ということで
力学的エネルギーは保存されると考えてよいことになります。

 

　②円運動の運動方程式

 

 

　A．最下端での張力

 

　鉛直最下端での張力\(T_1\)を求めます。
重力による位置エネルギーの基準を最下端にとり、このときのおもりの速さを\(v_1\)として、
\begin{eqnarray}
　力学的エネルギー保存則&：&\frac{1}{2}mv_o^2+mgr=\frac{1}{2}mv_1^2+mg\times 0 \tag{5-3} \\
　円運動の運動方程式&：&m\frac{v_1^2}{r}=T_1-mg \tag{5-4}
\end{eqnarray}
となります。
このふたつの式は、おもりが最下端を通過する瞬間にだけ成り立つことに注意しましょう。

 

　（5-3）から\(v_1\)を求め、（5-4）に代入すれば、\(T_1\)が求まります。
\begin{eqnarray} v_1&=&\sqrt{v_o^2+2gr} \tag{5-5} \\
T_1&=&m\frac{v_o^2}{r}+3mg \tag{5-6}
\end{eqnarray}

 

B．最上端での張力

 

　鉛直最上端での張力\(T_2\)を求めます。
このときのおもりの速さを\(v_2\)として、
\begin{eqnarray}
　力学的エネルギー保存則&：&\frac{1}{2}mv_o^2+mgr=\frac{1}{2}mv_2^2+mg(2r) \tag{5-7} \\
　円運動の運動方程式&：&m\frac{v_2^2}{r}=T_2+mg \tag{5-8}
\end{eqnarray}
となります。このふたつの式はおもりが最上端を通過する瞬間だけに成り立つことに注意しましょう。

 

　（5-7）から\(v_2\)を求め、（5-8）に代入すれば、\(T_2\)が求まります。
\begin{eqnarray} v_2&=&\sqrt{v_o^2-2gr} \tag{5-9} \\
T_2&=&m\frac{v_o^2}{r}-3mg \tag{5-10}
\end{eqnarray}

 

　まとめとしてもう一度上げておきます。

　糸がたるむ条件は、張力を式で表し、\(張力\lt0\)から求めます。
静止している場合は、糸がぴんと張っているという条件で張力を求めるわけですから、
糸がたるむ条件は、運動している場合の張力について問われることになります。
これまでの例を用いて、糸がたるむ条件を考えます。

 

（1）　\(張力\lt0\)の根拠

 

 

　これまでの例題で、おもり等に糸の張力がはたらく場合、
おもりが糸に引っ張られる向きに張力を描いています。
これが、おもりにはたらく張力の向きです。

 

　大きさが同じで向きが逆の力が糸にもはたらいているわけで、
それを図示すると、図6-1の(a)のようになります。

 

　つまり、張力が正ならば糸が外側に引っ張られ、たるむことはありません。

 

　一方、張力が負というのは、(b)の場合で、
糸をたるます向きに力がはたらくことがわかります。

 

 

 

 

（2）　たるむ条件とたるまない条件

 

A．　「Ⅲ．運動している場合の張力」の【例】

 

【例1】で求めた張力は、
\begin{equation}　T=\frac{Mmg}{M+m} \tag{3-4}　 \end{equation}
　常に、\(T\gt 0\)なので、たるむことがありません。
　これは、【例1】の設定から当然の結果です。

 

【例2】【例3】も同じようにたるむことはありません。

 

 

 

　【例4】の張力は、
\begin{equation}
T=\frac{m_2(2m_1g-\rho Vg+kv)}{m_1+m_2} \tag{3-23}
\end{equation}
　たるむ条件は\(T\lt 0\) ですから、
\begin{equation} 2m_1g-\rho Vg+kv\lt 0 \end{equation}
　この式を吟味しましょう。
左辺が最も小さくなるのは、\(v=0\)の場合です。（\(v\)は負にならないという設定です。）
つまり、固定していたおもりを離して、おもりA、Bが動き出す瞬間です。
このときが、最も糸がたるみやすいときです。
　このとき、糸がたるむ条件は、
\begin{eqnarray} \rho Vg&\gt& 2m_1g 　\\
\rho&\gt& \frac{2m_1}{V} \\
\rho&\gt& 2\rho_s \\
ここで、\rho_sはおもりAの密度です。
\end{eqnarray}

 

 

B．「Ⅴ．円運動している場合の張力」の”鉛直面内で円運動している場合の張力”の【例】

 

　鉛直面内で円運動してる場合について糸がたるまない条件を考えます。
もう一度、下に図5-3を掲げます。

 

 

　（a）の初期状態から（c）の最上端に至るまでの間に糸がたるまないための\(v_o\)の条件を求めます。

 

　（5-10）式に最上端での糸の張力\(T_1\)の式が表されているので、
（5-10）式において\(T_1\gt 0\)とするのが、たるまないための条件となりそうですが、
（a）の初期状態から（c）の最上端に至るまでのすべての時間で、\(T_1\gt 0\)が成り立つ条件である必要があります。

 

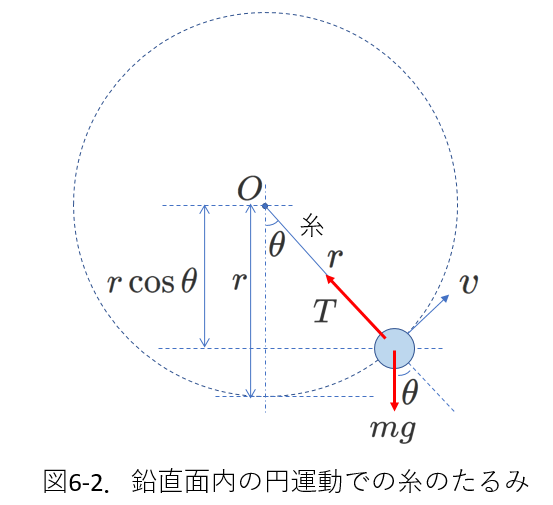
　今、（b）鉛直最下端から（c）鉛直最上端までの、糸のたるみについて考えます。
そのために、この領域で糸の張力を求めます。

 

 

　おもりにはたらく力は糸からの張力と重力です。図示すると、図6-2のようになります。
力学的エネルギー保存の式と円運動の運動方程式を立てると、
\begin{eqnarray} \frac{1}{2}mv_o^2+mgr&=&\frac{1}{2}mv^2+mgr( 1-\cos\theta) \tag{6-1} \\
m\frac{v^2}{r}&=&T-mg\cos\theta 　\tag{6-2}
\end{eqnarray}
注）上式で、図5-3(b)では\(\theta=0\)、図5-3(c)では\(\theta=\pi\)であることを確認してください。
\(\theta=0\)のときは、図5-3(b)と同じ状態ですから、上のふたつの式は（5-3）（5-4）式と一致します。
\(\theta=\pi\)のときは、図5-3(c)と同じ状態ですから、上のふたつの式は（5-7）（5-8）式と一致します。

 

（6-1）式から、
\begin{equation} v=\sqrt{v_o^2+2gr\cos\theta} \tag{6-3} 　\end{equation}
注）\(\theta=0\)で（5-5）と同じ、\(\theta=\pi\)で(5-9)式と同じ式です。

 

（6-3）式を（6-2）式に代入して\(T\)を求めます。
\begin{equation} T=m\frac{v_o^2}{r}+3mg\cos\theta \tag{6-4} \end{equation}
\(T\)が最小となるのは、\(\theta=\pi\)のとき（つまり、最上端に達したとき）で、
\begin{equation} T=m\frac{v_o^2}{r}-3mg 　\tag{6-5} 　\end{equation}
したがって、このときに\(T\gt 0\)であれば、(b)から(c)の間で糸がたるむことはないことがわかりました。
以上より、\(v_o\)の条件は、\(v_o\gt\sqrt{3gr}\)　(6-6)となります。

 

　さて、この場合、おもりが最上端まで達することができる、という条件も検討する必要があります。
おもりが最上端まで達することができなければ(6-5)式の意味がありません。

 

 

　これは、\(\theta=\pi\)のときの（6-3）式の根号の中が\(0\)以上という条件になります。
したがって、\(v_o\gt\sqrt{2gr}\)です。

 

この条件は、（6-6）式に含まれるので、
（6-6）式が「糸がたるまない」「おもりが最上端に達する」のふたつを同時に満足する条件となります。

関連ページ

作図

物理の問題を解く場合、図を描くことは必須と言えます。図を活用することで、考察が進み、その結果ミスを減らすことができます。図を活用する場合の注意点を説明しています。

運動方程式

物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。

モーメントの考え方

力のモーメントについて、基本的注意事項のいくつかを説明しています。

運動量保存則を使う問題

運動量保存則は、力学でも最も重要な概念のひとつです。運動量が保存される場合と保存されない場合について説明し、例題を掲げました。

運動エネルギーと仕事の関係

運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。

力学的エネルギー保存則を考える

力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。

単振動

単振動に関する問題を解くときに必要な知識について説明をしています。

力積

力学は物理の基礎とも柱とも言えます。しっかり勉強して理解を深めましょう。

円運動

円運動を考えるには、向心力を用いて運動方程式を立てるか、遠心力で力のつりあいを考えます。円運動の問題は難しく感じますが、出題のパターンは多くありません。

二体問題　Ⅰ

互いに力を及ぼし合う二つの物体の動きを考えます。