Ⅰ.変位、速度、加速度
座表軸が示されている場合、速度や加速度の正の向きは座標軸の正の向きと一致します。
ただし、問題に向きが指定されている場合には、それに従いましょう。
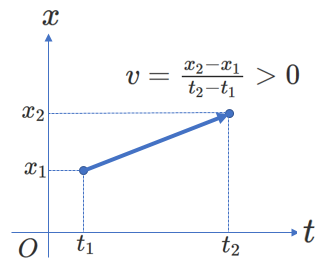
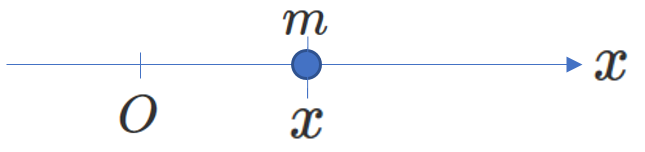
今、小物体が\(x\) 軸上を移動する運動(1次元の運動)を考え、その座標を\(x\)、速度を\(v\)、加速度を\(\alpha\)とします。
\(\Delta t>0\) のとき、\(\Delta x>0\) ならば、時間がたつにつれて、上図および右図で、\(m\)は \(+x\) の向きに動きます。このとき、\(\frac{\Delta x}{\Delta t}>0\)、すなわち、\(v>0\) ですから、\(+x\) の向きが\(v\) の正の向きになります。
次に、加速度の正の向きを考えます。\(\alpha=\frac{\Delta v}{\Delta t}\) ですから、時間が経過したとき(すなわち、\(\Delta t>0\) のとき)、\(\Delta v>0\) ならば、\(\alpha>0\) となります。そこで、「 \(\Delta t>0\) のとき、\(\Delta v>0\) 」となる場合の加速度の向きを調べます。
\(v>0\) と、\(v<0\) の場合に分けて考えます。
(ⅰ)\(v>0\)、かつ、 \(\Delta v>0\)の場合
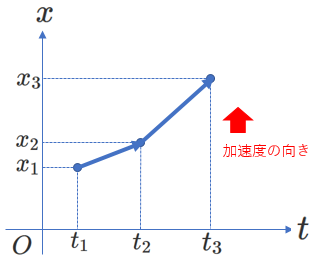
(ⅱ)\(v<0\)、かつ、 \(\Delta v>0\)の場合
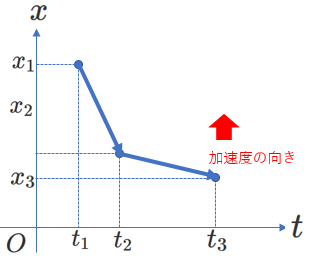
どちらの場合でも、加速度の向きは\(x\) 軸の正の向き(\(+x\)向き)となります。これが、加速度の正の向きです。
Ⅱ.運動量保存則での各項の正負を考える
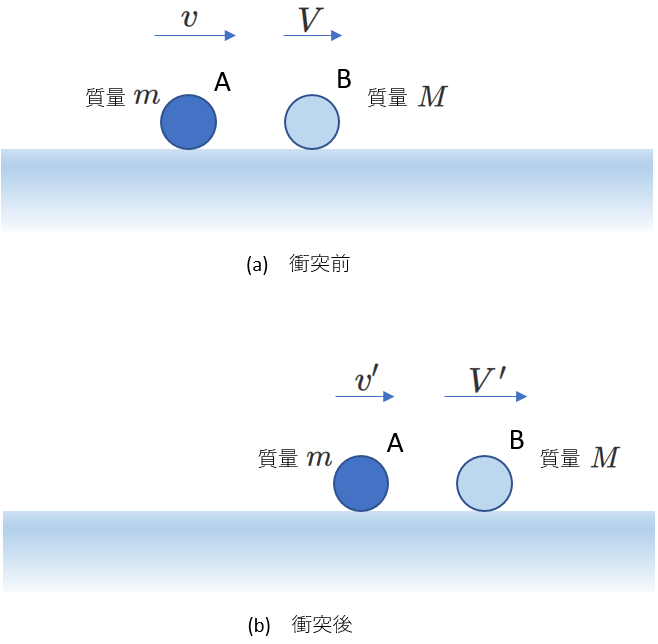
なめらかな床上の物体Aと物体Bの衝突を考えます。
物体Aの質量は\(m\)で、衝突前の速度は\(v\)、
物体Bの質量は\(M\)で、衝突前の速度は\(V\)とします。
(右図を参照)
右向きを速度の正の向きとして、衝突後の2つの物体のそれぞれの速度\(v'\)、\(V'\)を求めてみましょう。
運動量保存の式を立てると、
\begin{equation}
mv+MV=mv'+MV' \tag{2-1}
\end{equation}
はね返り係数(反発係数)を\(e\)として、はね返り係数の式を立てると、
\begin{equation}
e=-\frac{V'-v'}{V-v} \tag{2-2}
\end{equation}
2つの方程式を連立させて解けば、\(v',V'\)を、\(m,M,v,V,e\)で表すことができます。
一方、衝突後、物体Aは物体Bによって跳ね返されて左向きに進むはずだと考え、
右下図をもとに立式する人もいるでしょう。
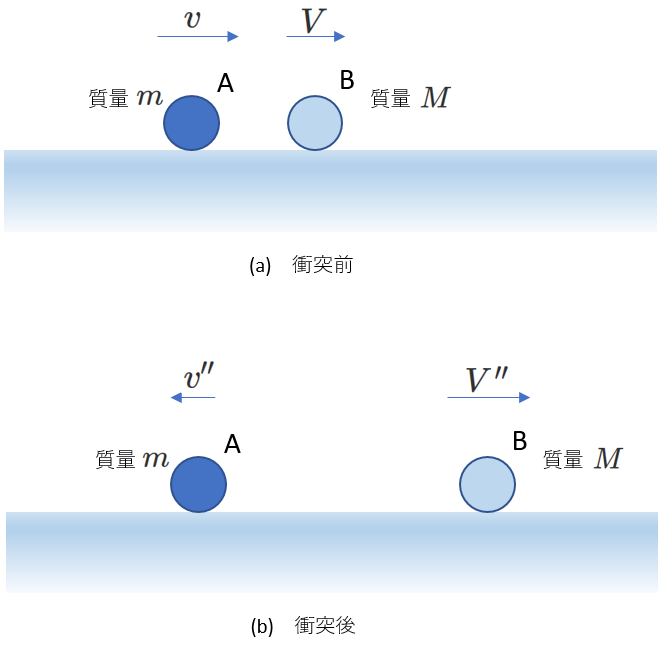
この図にしたがって運動量保存の式を立てると、
\begin{equation}
mv+MV=-mv''+MV'' \tag{2-3}
\end{equation}
また、跳ね返り係数の式は
\begin{equation}
e=-\frac{V''-(-v'')}{V-v} \tag{2-4}
\end{equation}
(2-3)、(2-4)式も、式として正しい式ですが、
\(v''\)を、速度の大きさ(速さ)として立式していることに注意しましょう。
一方、(2-1)式、(2-2)式では、\(v'\)を速度として立式しています。
この立場の違いを理解しましょう。
(2-3)式の右辺の\(-mv''\)の\(-\)は、「\(v''\)は速度の正の向きとは逆である」ことから付けた負号です。
衝突後の物体Aの速度を\(-v''\)と表すことは、\(v''>0\)のとき速度の向きは左向きであると考えていることになります。
したがって、問題が「右向きを速度の正の向きとして・・・答えよ」となっている場合には、
\(v''\)ではなく、\(-v''\)を答えなければなりません。
Ⅲ.単振動の運動方程式
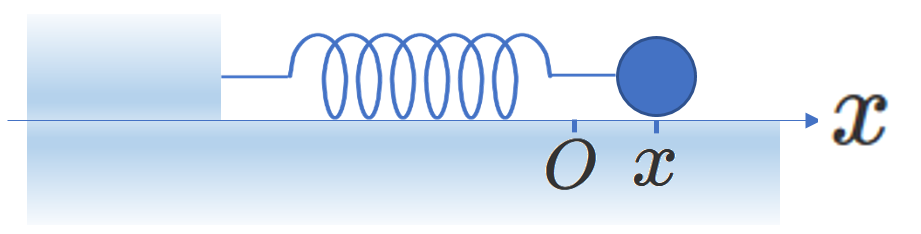
右の図のように、\(x\)軸を設定し、
おもりが原点\(O\)にあるとき、ばねは自然長であり、
おもりが座標\(x\)にあるときの加速度を\(\alpha\)として
運動方程式を立てれば、\begin{equation} m\alpha=-kx \tag{3-1} \end{equation}
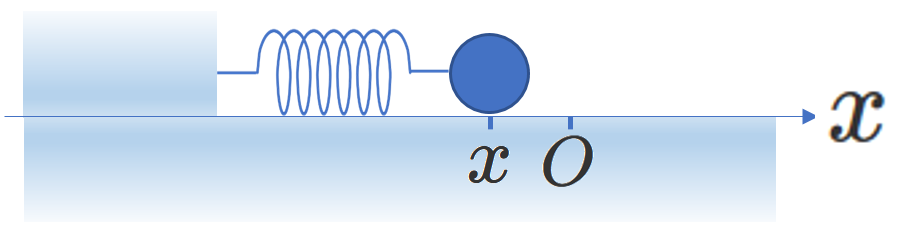
次に、右図のように、おもりが\(x<0\)の領域にあるとき
つまり、ばねが縮んでいる状態で運動方程式を立ててみましょう。
当然、(3-1)式と同じ式になるはずです。
ばねの縮み量は\(-x\)、
したがって、ばねの力の大きさは\(k(-x)\)で、向きは右向きなので、
運動方程式を立てれば、
\begin{equation} m\alpha=-kx \tag{3-2} \end{equation}
と、(3-1)式と同じになります。
ここで注意するべきは、「ばねの縮み量は\(-x\)」の部分です。
\(x<0\) なので、正しい縮み量(\(>0\))は\(-x\)で表されます。
座標軸の負の領域で運動方程式を考えると、ミスしやすいことがわかるでしょう。
運動方程式は座標軸が正の領域で立てる方が、立式ミスが少なくなります。
Ⅳ.逆起電力の正負
コイルの誘導起電力の項の符号の正負は、判断が難しいです。
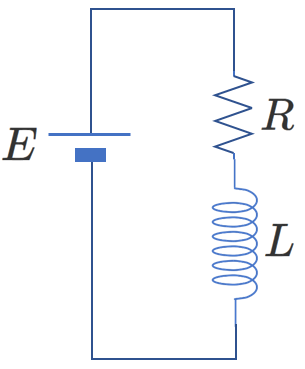
例えば、右の回路についてキルヒホッフの第二法則の式を立ててみましょう。
最初にすることは、流れる電流の正の向きを定めることです。
どちら向きでも良いですが、
電池(電源)が流そうとする向きに電流の正の向きを定めると、
そのあとの考察が楽になります。
そこで、次の図のように電流の正の向きを決めます。
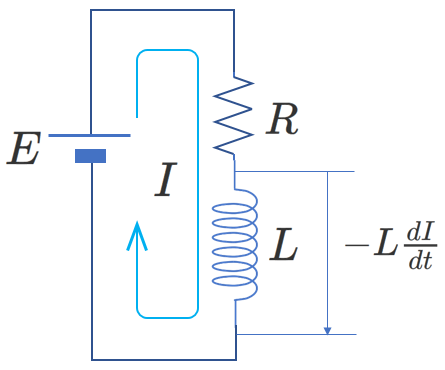
自己インダクタンスを\(L\)として、自己誘導起電力\(V\)は、
\begin{eqnarray} V&=&-L\frac{\Delta I}{\Delta t} \\
あるいは、 V&=&-L\frac{dI}{dt}
\end{eqnarray}
注)負の符号は、電流の変化を打ち消す向きに誘導起電力が生じることを意味します。
また、キルヒホッフの第二法則は、
キルヒホッフの法則 Ⅱ
回路中の一回りの閉じた経路について、 起電力の和=電圧降下の和
そこで、\(Eと-L\frac{dI}{dt}\)を左辺に、\(R\)による電圧降下\(RI\)を右辺に置いて、
キルヒホッフの第二法則を表す式は、次のようになります。
\begin{equation} E-L\frac{dI}{dt}=RI \tag{7} \end{equation}
コイルの自己誘導起電力は\(-L\frac{dI}{dt}\)、起電力という名前がついているので、左辺にそのまま入れて、式をたてます。
さて、「負の符号は、電流の変化を打ち消す向きに誘導起電力が生じることを意味します。」を確認します。
そこで、時刻が \(t\)から\(t+\Delta t (\Delta t>0)\)に経過する間に、
電流が\(I\)から\(I+\Delta I\)に変化すると仮定して、
\(\Delta I>0 (電流が増加)、\Delta I=0 (電流が一定)、\Delta I<0\) (電流が減少)の3つの場合に分けて考えます。
1)\(\Delta I>0\)の場合
この場合は、\(-L\frac{\Delta I}{\Delta t}<0\)です。
誘導起電力は、右上図の電流\(I\)とは逆の向きに電流を流そうとします。
つまり、電流の増加を打ち消す向きです。
2)\(\Delta I<0\)の場合
この場合は、\(-L\frac{\Delta I}{\Delta t}>0\)です。
誘導起電力は、右上図の電流\(I\)と同じ向きに電流を流そうとします。
つまり、電流の減少を打ち消す向きです。
3)\(\Delta I=0\)の場合
この場合は、\(-L\frac{\Delta I}{\Delta t}=0\)です。
電流が変化しないので誘導起電力は0です。
以上のように、
「負の符号は、電流の変化を打ち消す向きに誘導起電力が生じることを意味します。」を確認できました。
最後に、電流の正の向きを最初に定めた電流の向きと逆の向きに決めた場合、キルヒホッフの第二法則がどのように書けるかを考えます。
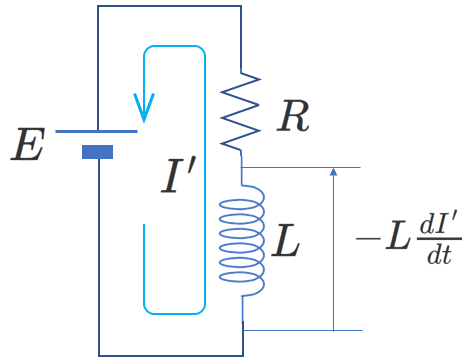
それを右図に示します。ここで、流れる電流を(これまでの説明の\(I\)と区別するために)\(I'\) とします。
第二法則の左辺(起電力の和)は、
定めた電流の正の向きに電流を流そうとする起電力が正ですから、
電池の起電力は\(-E\)で表されます。
誘導起電力は\(-L\frac{\Delta I'}{\Delta t}\)です。
また、電圧降下は\(RI'\)です。
したがって、求める式は、
\begin{equation} -E-L\frac{\Delta I'}{\Delta t}=RI' \tag{8} \end{equation}
です。
\(I'\)と\(I\)の流れる向きは逆ですから、\(I'=-I\)の関係があります。
これを(8)式に代入すると、(7)式が得られることから、(7)式と(8)式は等価であることがわかります。
つまり、
電流が流れる向きをどちらに決めても良いのですが、
電池(電源)が流そうとする向きに電流の正の向きを定めると、そのあとの考察が楽になります。
であることがわかります。
Ⅴ.熱力学の正負
一例として、熱力学の第一法則を考えます。
教科書には、
熱力学第一法則
\begin{eqnarray} \Delta U=Q+&W& \\
\Delta U[J]&:& 内部エネルギーの変化 \\
Q[J]&:& 物体(気体)に与えた熱量 \\
W[J]&:& 物体(気体)にした仕事
\end{eqnarray}
この式を各項の正負まで正しく覚えるのはたいへんです。
式を丸暗記するのと一緒に、式の意味を吟味しておきましょう。
この式に依れば、
「物体(気体)に与えた熱量\(Q\)」が増えれば、右辺の\(Q\)の符号は\(+\)ですから、「内部エネルギー\(\Delta U\)」は増加します。
これは、現象に合っています。
「物体(気体)にした仕事\(W\)」が増えれば、右辺の\(W\)の符号も\(+\)ですから、「内部エネルギー\(\Delta U\)」は増加します。
これも、現象と合致しますね。
さて、問題によっては、
\(Q\)が、「物体(気体)に与えた熱量」ではなく、「物体(気体)が放出する熱量」であったり、
\(W\)が、「物体(気体)にした仕事」ではなく、「物体(気体)が(外部に)した仕事」であったりするので、
熱力学の問題では問題文をしっかり読み、細かい点に留意することが大事です。
「物体(気体)に与えた熱量」 = 「物体(気体)が受け取った熱量」 = \(-\)「物体(気体)が放出する熱量」
「物体(気体)にした仕事」 = 「物体(気体)がされた仕事」 = \(-\)「物体(気体)が(外部に)した仕事」
です。
したがって、
熱力学第一法則は、
\begin{eqnarray}
\Delta U[J]&:& 内部エネルギーの変化 \\
Q[J]&:& 物体(気体)に与えた熱量 \\
W[J]&:& 物体(気体)が外部にした仕事 \\
であれば、 \Delta U=Q-&W& \\
と書けます。
\end{eqnarray}
式の意味を確認しておきましょう。
この式に依れば、
「物体(気体)が外部にした仕事\(W\)」が増えれば、
右辺の\(W\)の符号は\(-\)ですから、「内部エネルギー\(\Delta U\)」は減少します。
現象とぴったり合致しますね。
正しい式だとわかります。
\(Q\)や\(W\)が問題文に与えられていないときに、自分で定義して使う場合もあります。
そのときには、「\(Q\)は熱量、\(W\)は仕事」という説明ではなく、
「\(Q\)は気体に与えた熱量、\(W\)は気体が外部にした仕事」と、詳しい説明を付けます。
途中で別の問題を解いてから戻って解くときや、答案を見直す際に、混乱することなく、ミスも減らせます。
関連ページ
- 次元に注意する
- 次元(単位)を考えることで、答えの間違いや計算ミスを発見することができます。その考え方を紹介しています。