モーメントの考え方

トップページ＞力学＞モーメントの考え方

Ⅰ．静止している場合のモーメントの式

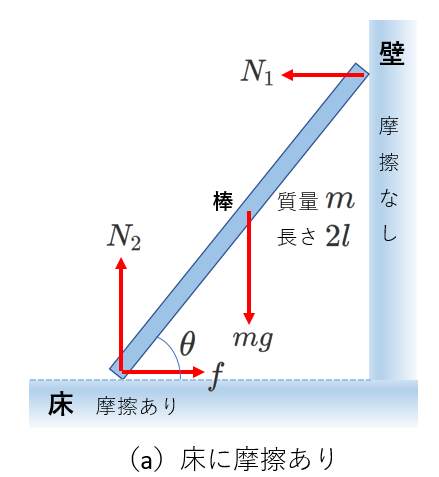
モーメント　摩擦あり

　右図で、棒が壁に立てかけられた状態で静止しています。

　床と棒の間には摩擦があり、壁と棒の間には摩擦がありません。
棒の質量は\(m\)、長さは\(2l\)、
棒と床のなす角度は\(\theta\)です。

　床と棒の間にはたらく摩擦力\(f\)を求めます。

棒に働く力は重力\(mg\)と、
　壁との接触部にはたらく、壁からの垂直抗力\(N_1\)、
　床との接触部にはたらく、床からの垂直抗力\(N_2\)、摩擦力\(f\)　です。

注）　垂直抗力\(N_2\)と摩擦力\(f\)の合力は、抗力と呼ばれます。

　さて、棒は剛体で、剛体のつりあいの条件は次のようになります。

剛体のつりあいの条件
　①合力が\(0\)、言い換えれば、力がつりあっている。
　②任意の点のまわりのモーメントの和\(0\)、言い換えれば、モーメントがつりあっている。

　棒は静止しているので、棒にはたらく力の合力は\(0\)、言い換えれば、力はつりあっています。
右図を参照して、
水平方向の力のつりあいと、鉛直方向の力のつりあいを考えると、
\begin{eqnarray} 水平方向　　　f&=&N_1 \tag{1} \\　
鉛直方向　　N_2&=&mg \tag{2} \end{eqnarray}

　未知数は、\(f、N_1、N_2\)の3つで、
もうひとつ方程式が必要ですから、モーメントのつりあいを考えます。

　上の剛体のつりあいの条件の②は、

静止している場合、モーメントの基準点をどこにおいて式を立てても良い

ということを言っています。

　ここでは、重心（棒の中心）のまわりのモーメントのつりあいを立式します。
反時計回りのモーメント=時計まわりのモーメントと表します。

\begin{equation} N_1l\sin\theta+fl\sin\theta=N_2 l\cos\theta \tag{3} \end{equation}

　（1）（2）式より、\(N_1=f\)、\(N_2=mg\)を（3）式に代入すると、

\begin{eqnarray} fl\sin\theta+fl\sin\theta&=&mgl\cos\theta \\
f&=&\frac{mgl\cos\theta}{2l\sin\theta}=\frac{mg}{2\tan\theta} \end{eqnarray}

　最大静止摩擦係数を\(\mu\)として、
棒が滑らない条件は、\(f\)が最大静止摩擦\(\mu N_2\)以下であることですから、

\begin{eqnarray} f=\frac{mg}{2\tan\theta}\leqq\mu mg \\
\tan\theta \geqq\frac{1}{2\mu}
\end{eqnarray}

　さて、

静止している場合、モーメントの基準点をどこにおいて式を立てても良い

を、確認するために、
モーメントの基準点を、棒の重心ではなく、棒の床に接触している部分にしてみましょう。

　すると、モーメントのつりあいの式は、
\begin{equation} N_1\times 2l\sin\theta=mg \times l\cos\theta \tag{4} \end{equation}

　さて、この式は（3）式と同じものではありません。
しかし、（1）式から\(N_1=f\)、（2）式から\(mg=N_2\)を（3）式に代入すると、
\begin{equation} N_1l\sin\theta+fl\sin\theta=N_2l\cos\theta \tag{4} \end{equation}
で、（4）式と同じになりました。

　つまり、力のつりあいの式（1）（2）式が成り立っている場合には、

静止している場合、モーメントの基準点をどこにおいて式を立てても良い

ということが言えます。

Ⅱ．力のつりあいとモーメントの式の数

　前の章の例題の検討から、
剛体が静止しているという問題にたいして、
力のつりあいでふたつの式、モーメントのつり合いで一つの式が得られるということが言えそうです。

　別の観点から見ると、
たいていの試験問題は、与えられた力は紙面に平行で2次元です。
ローレンツ力を除いて、3次元で考えることはほとんどありません。
2次元であれば、力のつりあいは2方向で成立、
モーメントのつりあいは、紙面に垂直な軸に対する回転を考えるだけですから
1軸で成立すると考えられます。
（紙面に平行なふたつの軸に対する回転を考える必要があるのは、
　紙面に垂直な方向の力がある場合であることに注意してください。）

　さて、Ⅰ．での議論から、
力のつりあいの式がある場合には、独立なモーメントのつりあいの式はひとつしかありません。
したがって、基準点をいくつか変えて、複数のモーメントのつりあいの式を立てても、意味がありません。

　以上のことから、方程式は全部で3つしかないので、
未知数が3個を超える場合には別の条件が必要になります。

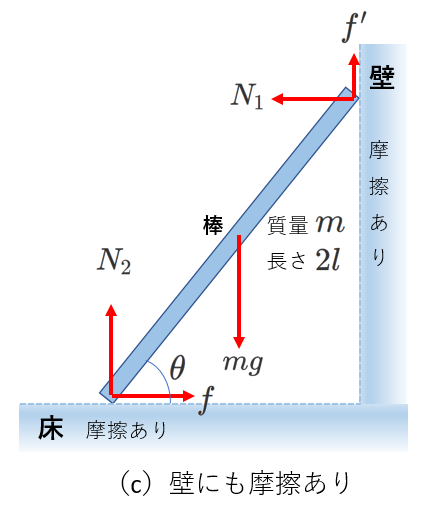
　例えば、右図のように、
壁にも摩擦があるとすると、
未知数は\(f、N_1、N_2、f'\)の4つになります。

　一方、方程式は3つしかないので、4つの未知数を求めることはできません。
仮に、このような問題があったとすれば、
問題文中に別の条件が示されているはずなので、見逃さないようにしましょう。

（たとえば、４つの未知数のうちひとつは大きさが与えられているとか、
　最大静止摩擦係数が与えられたうえで、\(f、または、f'\)が最大静止摩擦の大きさになっている、などです。

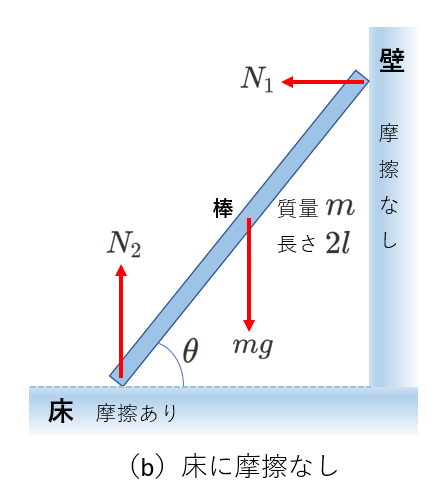
　では、棒と床、棒と壁の両方とも摩擦がない場合はどうでしょう。
未知数は、\(N_1とN_2\)の2個になりますが、方程式は3つできるのでしょうか？

　右図を見るまでもないですが、摩擦がなければ、棒は立てかけられていられず、滑り落ちてしまいます。
図で、\(N_1\)につりあう力がないことが、このことを表しています。

物理の大学入試問題をいかにして解くか