Ⅰ.力学の問題を解くポイント
1.系に働いている力を調べる
物体が接触しているところには必ず力が働きます。
垂直抗力、摩擦力、張力、浮力、液体や気体から受ける抵抗力
接触していなくても(離れていて)はたらく力があります。
重力(万有引力)、静電気力、磁気力、ローレンツ力、慣性力、遠心力
2.力がどの物体にはたらいているかを明確にする
力の作用点を明確にします。
そして、注目する物体にはたらく力をすべて数え上げます。
3.立式する
静止している場合(および、等速度運動をしている場合)は力のつり合い、
加速度運動をしている場合は運動方程式や、
円運動の運動方程式を考えます。
着目する物体にはたらく力だけを取り上げ、他の物体やそれらにはたらく力を無視して式を立てます。
4.作図と、つり合いの式の立式

図には力の大きさ(つまり、絶対値)を記入します。
力の向きは矢印の向きで示します。
その力が正のときの向きが、図に示した向きとなります。
計算した結果、力が負の値になったときは、
力の向きは図に描いた向きの逆であったことになります。
力のつり合いを考える場合、2つの方法があります。
a) 反対方向の力の大きさが等しいという式を立てる方法
(以降では、これを「力のつり合いを考える」方法と説明しています。)
右図において、\(A=B\)と表現します。
b) 合力が\(0\)という式を立てる方法-その1
右図において、上向きを力の正の向きと考えて、\(A+(-B)=0\)と表します。
c) 合力が\(0\)という式を立てる方法-その2
\(A\)と\(B\)の合力が\(0\)を表すのに、
上向きを力の正の向きと考えて、\(A+B=0\)と考える場合もあります。
これから、\(B=-A\)となり、
\(B\)は\(A\)とは逆の向きということがわかります。
つまり、この式を立てる場合は、\(A,B\)を力の大きさではなく、
向きを含んだベクトルと考えていることになります。
問題を解くとき、右上のような図を描く場合が多く、これに合わせるために、a)b)の立場をとるのが普通です。
注) 速度(速さ)の場合にも、a)b)の立場をとる人、c)の立場をとる人がいます。
c)を考える人が多いようですが、自分にあった方法で解くのが良いでしょう。
ただし、問題の多くは、速度の正の方向を決めているので、それに沿って解答する必要があります。
Ⅱ.力の表し方 (1)
力は大きさと向きを持つベクトル量です。
そこで、図に力を示す場合、矢印が用いられます。
矢印の各部分は、下の図に示したような意味を持っています。
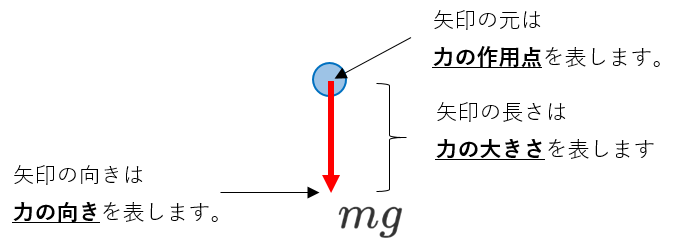
力の図を書くときに注意するのは、
作用点を明確に示す
ことです。
その力は、どの物体にはたらいているか、はっきりと示しましょう。
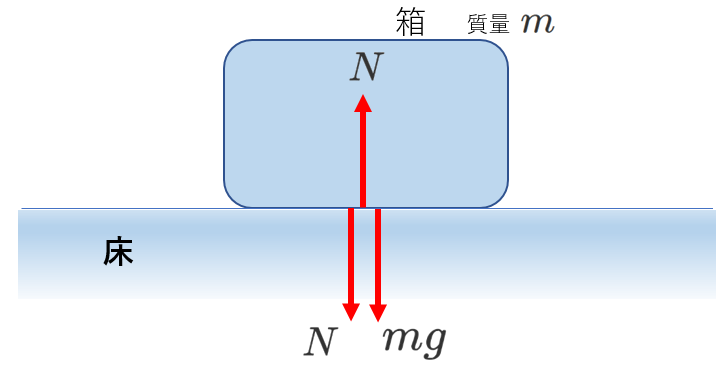
床の上に置かれた(静止した)質量\(m\)の箱に働く力を考えてみましょう。
箱には、重力と床からの垂直抗力が働き、
床には、箱から垂直抗力が働きます。
そこで、右図のように力の図を表したとすると、
箱に働く力がどれであるかわかりにくいですね。
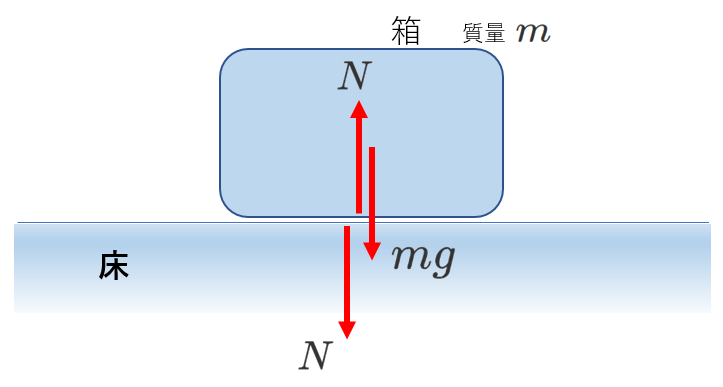
その下の図のように描くとわかりやすいです。
ここで、箱を床から少し離して描いています。
重力\(mg\)の作用点は、箱の重心付近に置きました。
\(N\)の作用点は、床と箱の境界線から少し離しています。
作用点を明確にする理由は、運動方程式を立てやすくするためです。
運動方程式はひとつの物体に注目して立式します。
その物体にはたらく力を数え落とさないように、
同時に、誤った力を数え上げないように、立式します。
Ⅲ.力の表し方 (2) 静止している物体

右図は、床の上に物体B、さらにその上に物体Aが置かれている場合にはたらく力の図を描いたものです。
力には、接触部にはたらく力と、離れてはたらく力があります。
接触部にはたらく力は、垂直抗力、摩擦力、張力、浮力、液体や気体から受ける抵抗力などです。
離れてはたらく力は、重力(万有引力)、静電気力、磁気力、ローレンツ力、慣性力、遠心力などです。
右図では、
AとBに重力がはたらきます。
接触しているAとBには垂直抗力\(N\)がはたらきます。
同様に、接触しているBと床には、垂直抗力\(N'\)がはたらきます。
右図をもとに、\(N\)と\(N'\)を求めてみましょう。
A,Bにはたらく力をはっきりさせるために、物体Aだけ、および、物体Bだけを抜き出した図を描いてみました。

物体Aは静止しているので、
物体Aだけ抜き出した右図(a)においても、
物体Aは静止していなければなりません。
Aが静止している理由は、
下に物体Bがあるからではなく、物体Bから力(垂直抗力)を受けるからです。
したがって、図(a)でも静止するという条件を満たしているはずです。
「静止、または、等速度運動」=「力がつりあっている」、あるいは、「合力が0」
ということから、「力のつりあい」を考えて式を立てると、
\begin{equation} N=mg \end{equation}
です。
この式は、\(N\)の大きさと\(mg\)の大きさが等しいことを示しています。
また、「合力が0」と考えて式を立てると、
\begin{equation} N+(-mg)=0 \end{equation}
です。
Aにはたらく垂直抗力\(N\)の向きを正とすると、重力は向きも含めて\(-mg\)です。
ふたつの式は等価ですが、その示す意味が少し異なります。
次に図(b)を参考にして、物体Bにはたらく力のつり合いを考えて式を立てると、
\begin{equation} N'=N+Mg=(m+M)g \end{equation}
となります。
Ⅳ.力の表し方 (3) 運動している物体
次に運動(加速)している場合の力の図を考えます。

右の図では、質量\(m\)の物体Aが斜面を滑っています。
Aと斜面の間には摩擦はないものとします。
すると、Aにはたらく力は重力\(mg\)と垂直抗力\(N\)のふたつです。
右図では、のちほど、合力を考えたり、力を成分に分解するのに都合が良いように、
\(mg\)の作用点を物体Aの重心ではなく、\(N\)の作用点に置いています。
注)このホームページのほかの章でも、理解しやすいようにと、
重力の作用点を重心ではないところに描いている場合があります。

静止している場合と同じように、斜面を取り除きます。
斜面があるから、斜面に沿って加速するわけですが、
「斜面に沿って(水平面に対して角度\(\theta\)で)下向きに力がはたらくから、Aは斜面に沿って加速する。」
と、考えます。

つまり、右図に示すように、
重力\(mg\)と垂直抗力\(N\)の合力が斜面に沿った向きになるはずです。
この大きさは、図から\(mg\sin\theta\)であることがわかります。
この合力は、斜面に垂直な成分を持っていません。
これは、\(mg\)と\(N\)の斜面に垂直な成分の合力が0であるからです。
(\(mg\)と\(N\)の斜面に垂直な成分がつりあっているとも言えます。)

教科書などでは、
重力\(mg\)を斜面に沿った方向(\(x\)方向)と、それに垂直な方向(\(y\)方向)の成分に分解して考える方法が示されています。
これを右図に示します。
斜面に沿った方向の力の大きさが\(mg\sin\theta\)であるのは、上と同じですが、
こちらは、\(N=mg\cos\theta\)であることも、直ちにわかります。
Ⅴ.力の表し方 (4) 観測場所の違い
運動を観測する場所が変わると、
力の図が変わる場合があります。
慣性力や遠心力などがはたらく場合です。
慣性力も遠心力も、観測者自身が加速度運動をしているために生じる見かけ上の力です。
したがって、加速度運動していない(すなわち、静止している)観測者は
慣性力も遠心力も観測できません。
これが、観測場所により力の図が異なる理由です。
1) 鉛直上向きの加速度\(a\)で上昇するエレベータの床に置かれた小物体A(質量\(m\))の運動
観測者がエレベータの外にいる場合と、
エレベータの中にいる場合とで、比較をしてみましょう。
(a)観測者がエレベータの外にいる場合
観測者が見る小物体の運動は、
鉛直上向きの加速度の大きさ\(a\)の等加速度運動です、
小物体にはたらく力は、重力と
(床に接触しているので) 床からの垂直抗力です。
次に図を載せます。
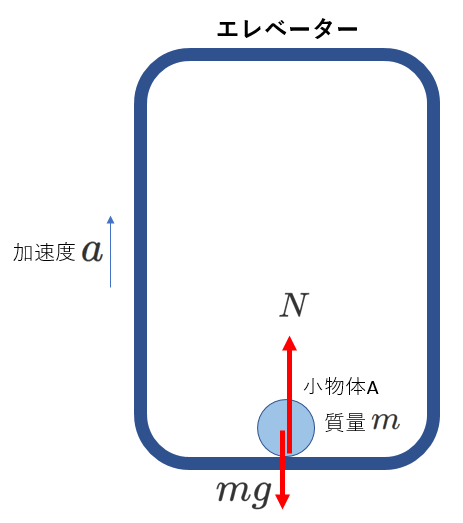
このふたつの力が小物体にはたらくので、
小物体は等加速度運動をするわけですから、
運動方程式を立てると、
\begin{equation} ma=N-mg \tag{1} \end{equation}
となります。
この式は、右欄の(2)式(3)式と等価ですが、立式の根拠の違いを反映して、微妙に形が異なっていることに注目してください。
(b)観測者がエレベータの中にいる場合
エレベータの中の小物体は、
観測者には床上に静止して見えます。
また、小物体が重くなっていることを観測できます。
このことから、自分自身が加速していると想像できます。
慣性力を考えることになります。
小物体は静止しているので、力はつり合っています。
小物体にはたらく力は、重力と慣性力、
(小物体は床に接触しているので)床からの垂直抗力です。
図に描けば、
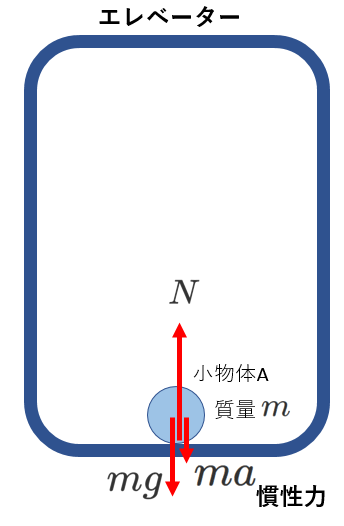
となります。
3つの力のつりあいは、
\begin{equation} N=ma+mg \tag{2} \end{equation}
3つの力の合力=0という式を立てると、
\begin{equation} N-ma-mg=0 \tag{3} \end{equation}
です。
これらの式は(1)式と等価ですが、立式の根拠の違いを反映して、微妙に形が異なっていることに注目してください。
2) 鉛直面内での円運動
次の例は、
点\(O\)で固定した糸の先に質量\(m\)のおもりをつなぎ、
おもりが点\(O\)の真下で静止しているときに、初速\(v_o\)を水平方向に与えます。
このとき、おもりは鉛直面内で円運動をしました。
この運動について、どのような力がはたらいているのかを考えます。
観測者が系の外にいる場合と、観測者が運動するおもりの上にいる場合を比較します。
(a)観測者が系の外にいる場合
おもりに働く力は、重力と糸からの張力です。
張力は円運動の中心を向いています。
この向きはおもりの運動の向きに垂直です。
したがって、張力はおもりに仕事をしません。
さらに、重力は保存力ですから、おもりの力学的エネルギーは保存されます。
このことは、おもりの位置によって、おもりの速さが異なる非等速円運動をすることを意味しています。
おもりが、点\(O\)の真下にあるときに最も速く、おもりが上昇するにつれて、おもりの速さは小さくなります。
また、\(v_o\)の大きさにより、おもりが点\(O\)の真上に到達できるか否かが決まります。
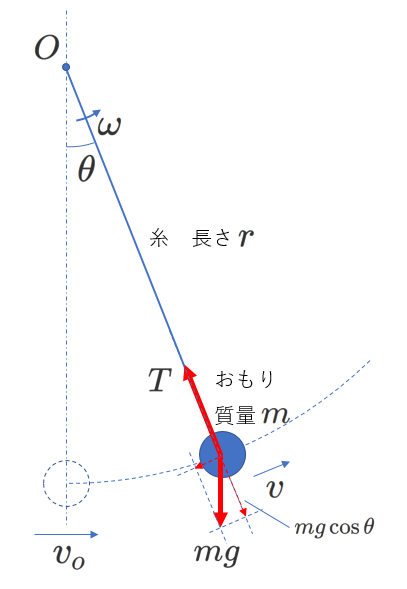
上図に示したように、糸が鉛直下向きとなす角度が\(\theta\)のときのおもりの速さが\(v\)、糸の張力が\(T\)、角速度\(\omega\)であるとします。
円運動の中心方向の運動方程式は、
受けている力の中心方向成分を\(F\)として、
\begin{eqnarray} mr\omega^2&=&F \\
または、m\frac{v^2}{r}&=&F \end{eqnarray}
上図で、円運動の中心方向の力(すなわち向心力)の大きさは、\(T-mg\cos\theta\)です。
したがって、円運動の運動方程式は、
\begin{equation} m\frac{v^2}{r}=T-mg\cos\theta \tag{4} \end{equation}
注1) \(T\not=mg\cos\theta\)であることに注意!
注2) 向心力という具体的な力があるわけではなく、向心力は円運動を維持する円運動の中心向きの力の便宜的な呼び名です。
本例では、張力と重力の中心向きの成分の合力が向心力を構成していると考えます。
向心力に含まれない成分、すなわち円運動の中心方向に垂直な方向の成分\(mg\sin\theta\)は、
おもりが進む向きの反対向きにはたらくので、おもりに対して負の仕事をします。
つまり、おもりの運動エネルギーを減らします。
(b)観測者が運動するおもりの上にいる場合
この場合、観測者は、おもりは動いていないと感じます。
つまり、力はつりあっていることになります。
おもりにはたらく力は、重力と糸からの張力に加えて、遠心力です。
おもりの上の観測者は円運動の中心と反対向きに力を感じます。
これは、おもりに生じる加速度(向心加速度)と反対向きに見かけの力(慣性力)がはたらいている、
と考えると説明がつきます。
遠心力は慣性力の一種です。
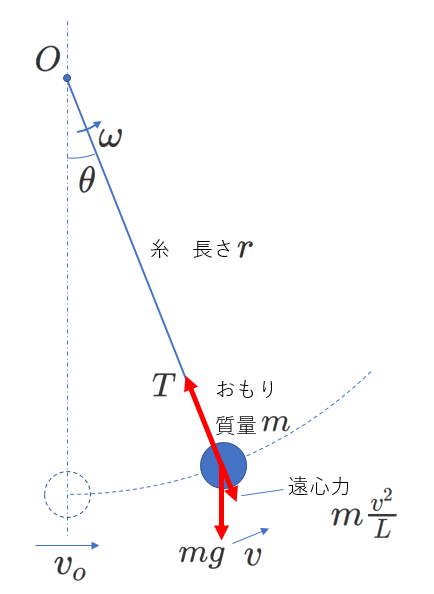
上図を参照して、糸が鉛直下向きとなす角度が\(\theta\)のときの
おもりの速さが\(v\)、糸の張力が\(T\)、角速度\(\omega\)であるとします。
遠心力は、
\begin{equation} mr\omega^2、または、m\frac{v^2}{r} \end{equation}
そこで、力のつりあいの式を立てれば、
\begin{equation} T=mg\cos\theta+m\frac{v^2}{r} \tag{8} \end{equation}
合力が\(0\)という式を立てれば、
\begin{equation} T-mg\cos\theta-m\frac{v^2}{r}=0 \tag{9} \end{equation}
この式は、(4)式と等価ですが、立式の根拠の違いを反映して、微妙に形が異なっていることに注目してください。
関連ページ
- 運動方程式
- 物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。
- モーメントの考え方
- 力のモーメントについて、基本的注意事項のいくつかを説明しています。
- 運動量保存則を使う問題
- 運動量保存則は、力学でも最も重要な概念のひとつです。運動量が保存される場合と保存されない場合について説明し、例題を掲げました。
- 張力
- 糸につながれたおもりの運動では、糸の張力を考慮します。張力を考える場合のヒントを説明しています。
- 運動エネルギーと仕事の関係
- 運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。
- 力学的エネルギー保存則を考える
- 力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。
- 単振動
- 単振動に関する問題を解くときに必要な知識について説明をしています。
- 力積
- 力学は物理の基礎とも柱とも言えます。しっかり勉強して理解を深めましょう。
- 円運動
- 円運動を考えるには、向心力を用いて運動方程式を立てるか、遠心力で力のつりあいを考えます。円運動の問題は難しく感じますが、出題のパターンは多くありません。
- 二体問題 Ⅰ
- 互いに力を及ぼし合う二つの物体の動きを考えます。