Ⅰ.力積を導く
この章では、教科書の内容に沿って力積の概念を導きます。
等加速度運動を考えます。
つまり、質量が\(m\)の物体に力\(F\)がはたらいて一定の加速度\(a\)で運動しています。
この物体に関する運動方程式は、
\begin{eqnarray} ma&=&F \tag{1-1} \\
したがって、a&=&\frac{F}{m} \tag{1-2}
\end{eqnarray}
このとき、物体の時刻\(t=0\)での速度を\(v_0\)とすると、
時刻\(t\)での物体の速度は、
\begin{eqnarray} v&=&v_0+\frac{F}{m}t \tag{1-3} \\
両辺にmを掛けてmv_0を移項すると、mv-mv_0&=&Ft \tag{1-4}
\end{eqnarray}
となります。
ここで、\(mv\)、\(mv_0\)は運動量、\(Ft\)は力積です。
(1-4)式は、[物体の運動量の変化量]=[物体に与えられた力積]を表しています。
注1)[運動量の変化]=[変化後の運動量]-[変化前の運動量]
注2)運動量の単位[kgm/s]と力積の単位[Ns]は同じ単位です。
言い換えると、\(Ft\)の力積が物体に与えられて、物体の運動量が\(mv_0\)から\(mv\)に変化したということです。
さて、\(v\)も\(F\)もベクトル量ですから、[運動量]も[力積]もベクトル量です。
ベクトル量を意識して、(1-4)式を書き改めれば、
\begin{equation} m\overrightarrow{v}-m\overrightarrow{v_0}=\overrightarrow{F}t \tag{1-5} \end{equation}
また、上記(1-4)式の導出過程では\(F\)は一定でしたが、\(F\)が時刻\(t\)の関数(時間によって\(F\)が変化する)場合にも、
力積を考えることができて、その時刻\(t_1\)から\(t_2\)の間に及ぼされた力積の大きさを\(I\)とすると、
\begin{equation} I=\int_{t_1}^{t_2} F(t)dt \tag{1-6} \end{equation}
と表すことができます。
この場合、(1-4)式は、次のようになります。
\begin{equation} mv(t_2)-mv(t_1)=\int_{t_1}^{t_2} F(t)dt \tag{1-7} \end{equation}
\(v(t_2)\)、\(v(t_1)\)はそれぞれ時刻\(t_2\)、\(t_1\)での速度を表します。
この式は、仮に\(F(t)\)が時刻によって複雑に変化しても、
時刻\(t_1\)と\(t_2\)の物体の運動量がわかればその時間にはたらいた力積が求められることを示しています。
\(t_1\)と\(t_2\)の間の運動量の詳しい変化の様子がわからなくても力積は求められます。
以上のことをもう一度考えるために、次の問題を考えてみます。
質量\(m\)の物体Aが\(x\)軸の正の向きに速さ\(v\)で進んでいるとします。
物体Aに大きさが\(F\)の力が\(x\)軸の正の向きに\(\Delta t\)だけはたらいて速さが\(v'\)になったとします。
\(v'\)を、\(F\)、\(\Delta t\)、\(m\)、\(v\)を使って表してみましょう。
物体Aの\(\Delta t\)間の加速度を\(\alpha\)とすると、
\begin{eqnarray} \alpha&=&\frac{v'-v}{\Delta t} \\
運動方程式を立てれば、 m\alpha&=&F \\
これより、 F&=&m\frac{v'-v}{\Delta t} \\
したがって、 v'&=&v+\frac{F\Delta t}{m}
\end{eqnarray}
これは、(1-1)式~(1-3)式の過程を見直したことになります。
もちろん、(1-4)式を使えば直ちに上式が得られます。
運動量保存則について、教科書では次のように説明されています。
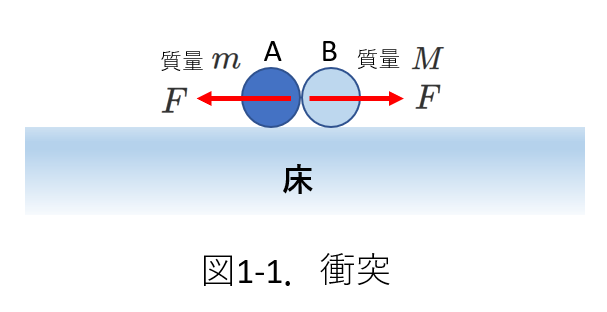
図1-1のAとBの衝突を考えます。質量はそれぞれ\(m、M\)です。
衝突時、衝撃力\(F\)がAに左向きに時間\(\Delta t\)の間はたらきます。
このとき、Bにも同じ大きさ\(F\)の力が右向きに同じ時間\(\Delta t\)はたらきます。
AとBについて、(1-4)式の[運動量の変化]=[力積]の式を表します。
衝突前のAとBの速度をそれぞれ\(v_A、v_B\)、衝突後のAとBの速度をそれぞれ\(v_A'、v_B'\)、右向きを速度の正の向きとして、
\begin{eqnarray} Aについて、&& v_A'-v_A=-F\Delta t \tag{1-8} \\
Bについて、&& v_B'-v_B=F\Delta t \tag{1-9}
\end{eqnarray}
ふたつの式から、\(F\Delta t\)を消去して、
\begin{eqnarray} -v_A'+v_A&=&v_B'-v_B \\
移項して整理すると、 v_A+v_B&=&v_A'+v_B' \tag{1-10}
\end{eqnarray}
このように、運動量保存則が導かれました。
この導出の過程で大切なことは、
AとBにはたらく力積の大きさが同じで向きが逆だということです。
これが運動量保存が成立する条件になります。
Ⅱ.運動量の変化=受けた力積
前章の(1-5)式のようにベクトルで表すことができるということは、運動量と力積の各方向成分のそれぞれについて、(1-4)式が成り立ちます。
\begin{eqnarray} m\overrightarrow{v}-m\overrightarrow{v_0}&=&\overrightarrow{F}t \tag{1-5} \\
つまり、m(v_x,v_y)-m(v_{0x},v_{0y})=&=&(F_x,F_y)t \tag{2-1} \\
\\
これから、mv_x-mv_{0x}&=&F_xt \tag{2-2} \\
mv_y-mv_{0y}&=&F_yt \tag{2-3}
\end{eqnarray}
衝突により運動の向きが変わる場合があります。
そのときには、運動量と力積をベクトル量と考えて、ベクトル図を描いて幾何学的に解くか、成分に分解して式を立てます。
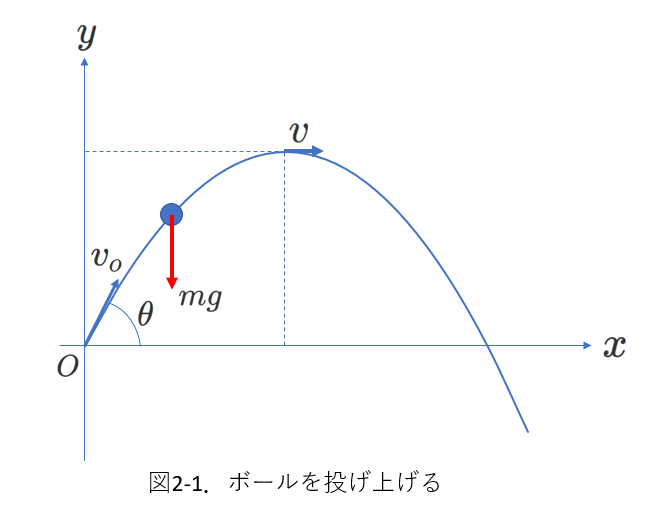
A.具体的に、質量\(m\)のボールを水平方向との角度\(\theta\)で投げ上げる場合について考えます。
初速は\(v_0\)、最高点での速さを\(v\)として、\(v_0\)から\(v\)になるまでにボールに与えられた力積\(I\)を計算します。
\(I\)を求める3つの方法を説明します。
①\(F\Delta t\)を計算します。
ボールにはたらく力は重力(上向きを正とし\(-mg\))です。
したがって、図2-1で、投げ始めから最高点に到達するまでの
時間がわかれば力積を計算できます。
\(v\)は水平方向右向きですから、速度の鉛直成分は\(0\)です。
そこで、\(t=0\)での速度の鉛直成分\(v_0\sin\theta\)が\(0\)になるまでの
時間を求めます。
\(a_y\)を加速度の鉛直成分として、上向きを正として、
鉛直方向の運動方程式は、\(ma_y=-mg\)より、\(a_y=-g\)です。
したがって、時刻\(t\)での速度の鉛直成分\(v_y\)は
\begin{equation} v_y=v_0\sin\theta-gt \end{equation}
求める時間を\(t_y\)として、上式において\(v_y=0\)とおいて、
\begin{equation} t_y=\frac{v_0\cos\theta}{g} \end{equation}
です。 したがって、力積\(I\)は、
\begin{equation} I=(-mg)\times \frac{v_0\sin\theta}{g}=-mv_0\sin\theta \tag{2-4} \end{equation}
となります。
②(2-2)(2-3)式をもとに運動量の変化から\(I\)を求めます。
\(x\)成分について、この向きに力ははたらかない(ボールの速度の水平方向成分に変化がない)ので、力積も\(0\)です。
\begin{eqnarray} x成分:&& mv-mv_0\cos\theta=0\times t \tag{2-5} \\
y成分:&& 0-mv_0\sin\theta=F_yt \tag{2--6}
\end{eqnarray}
(2-6)式から、(2-4)式と同じ結果\(F_yt=-mv_0\sin\theta\)が得られます。
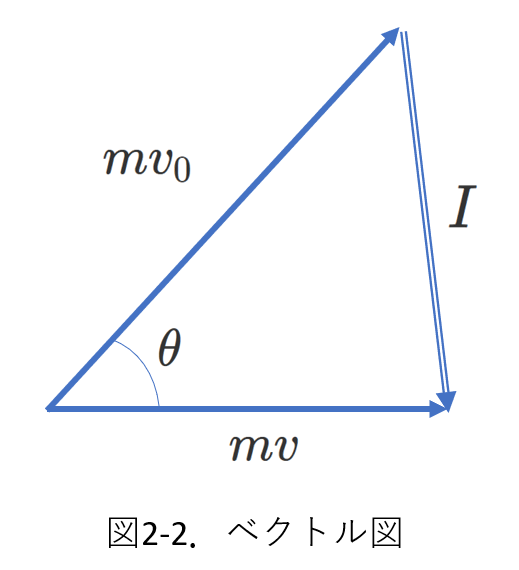
③ベクトル図から求めます。
運動量と力積のベクトル図を描いて求めます。
まず、適当に\(mv_0\)と\(mv\)を描き入れると、図2-2のようになります。
\(mv_0\)の\(x\)成分が\(mv\)に等しいことに気がつくと、
\(\overrightarrow{I}\)と\(m\overrightarrow{v}\)が垂直であることがわかります。
これを、図2-3に示しました。
この図から、\(I=-mv_0\sin\theta\)であることがわかります。
B.衝突の場合
右図2-4のように、質量\(m\)の小球Aが壁に衝突して、速さが\(u_0\)から\(u\)に変化しました。
このとき、Aにはたらいた力積\(I\)を右向きを正として求めます。
この場合、Aに対してはたらく衝撃力の大きさも時間もわからないので、[力]×[時間]の式を使って力積を計算することはできません。
運動量の変化から\(I\)を求めます。
\begin{equation} I=mu-(-mu_0)=m(u+u_0) \tag{2-7} \end{equation}
となります。
\(u\)、\(u_0\)は速さ(速度の大きさ)を表すので正の値です。
(2-7)式で、衝突前の速度は左向き(負の向き)ですから、その運動量は\(-mu_0\)と、負号が付きます。
\(I=m(u+u_0) \gt 0\)ですから、右向きの力積が壁からAに与えられたことがわかります。
注)この衝突の場合、運動量保存則は成り立ちません。
A単独では、\(I\)の衝撃力は外力になるので、成り立ちません。
また、壁の質量を\(M\)として、\(m(-u_0)+M\times 0=mu+M\times 0\) という保存の式も成り立ちません。
Aから壁には力積\(-I\)が与えられたはずですが、壁は動きません。
壁が動かないのは、Aから\(-I\)を受けると同時に、別のところから\(I\)の力積を受けているからです。
この別のところから受けた力はAと壁からなる系に対して外力となるので、運動量保存則は成立しません。
ただし、この、運動量保存則が成り立たない場合でも、はね返り係数を\(e\)として、
\begin{equation} e=-\frac{0-u}{0-(-u_0)}=\frac{u}{u_0} \end{equation}
は成り立ちます。
Ⅲ.運動方程式・力積・仕事
この章では、ひとつの例題を使って、次の5つについて検討します。
①運動方程式
②力積
③運動量保存則
④力学的エネルギー保存則
⑤運動エネルギーと仕事の関係
床の上に平板B(質量\(M\))が、さらにその上に物体A(質量\(m\))が乗っています。
床と平板Bの間に摩擦はありませんが、平板Bと物体Aの間には摩擦があります。
その動摩擦係数を\(\mu\)とします。
時刻\(t=0\)でBは静止、Aに初速\(v_0\)を与えます。
物体AとBに動摩擦力(大きさ\(\mu mg\))がはたらきます。
Aは右向きに進みますが、次第に速さは小さくなります。
Bは静止していましたが、動摩擦力により右向きに動き出します。
問:平板Bが\(l\)の距離進んだときのAとBの速さを求めます。
このとき、AはBに対して\(L\)の距離を進んだとすると、Aが床に対して進んだ距離は図3-1の(b)より\((l+L)\)となります。
この例題を使って、次の5つについて考えてみます。
①運動方程式
②力積
③運動量保存則
④力学的エネルギー保存則
⑤運動エネルギーと仕事の関係
①運動方程式
運動方程式から、「力積と運動量の変化量との関係」や「仕事と力学的エネルギーの変化量との関係」が導かれるわけで、
最も基本の考えです。
図3-1(c)にAとBにはたらく力を示しました。
図の文字式はそれぞれの力の大きさを示しています。
矢印は想定した力のはたらく向きです。
AもBも鉛直方向には運動しないのですから、鉛直方向の力はつりあっています。
Aにはたらく鉛直方向の力は、重力\(mg\)とBからの垂直抗力\(N\)のふたつで、これらはつりあっています。 つまり、
\begin{equation} N=mg \tag{3-1} \end{equation}
Bにはたらく鉛直方向の力は、重力\(Mg\)、Aからの垂直抗力\(N=mg\)(忘れずに)、床からの垂直抗力\(N'\)の3つです。
これらはつりあっていますから、
\begin{equation} N'=N+Mg=mg+Mg \tag{3-2} \end{equation}
です。
水平方向に運動するわけですから、AとBに水平方向にはたらく力を考えます。
図から、水平方向にはたらく力は摩擦力\(\mu mg\)です。
そこで、右向きを加速度の正の向きとし、AとBの加速度をそれぞれ\(a_A\)、\(a_B\)として、運動方程式は、
\begin{eqnarray} Aについて&& ma_A=-\mu mg \\
Bについて&& Ma_B=\mu mg
\end{eqnarray}
加速度を求めると、
\begin{eqnarray} Aについて&& a_A=-\mu g \tag{3-3} \\
Bについて&& a_B=\mu \frac{m}{M} g \tag{3-4}
\end{eqnarray}
です。
上の式から、\(a_A\)も\(a_B\)も一定値、すなわち、運動は等加速度運動であることがわかります。
したがって、時刻 \(t\) での速度を\(v_A\)、\(v_B\)として、
\begin{eqnarray} v_A&=&v_0-\mu gt \tag{3-5} \\
v_B&=&\mu\frac{m}{M}gt \tag{3-6} \end{eqnarray}
時刻 \(t\) のときに図3-1(b)の状態であったとすれば、
等加速度運動のときの変位を求める式を用いて、次の関係があります。
\begin{eqnarray} L+l&=&v_0t-\frac{1}{2}\mu gt^2 \tag{3-7} \\
l&=&\frac{1}{2}\mu\frac{m}{M}gt^2 \tag{3-8} \end{eqnarray}
さて、問題に答えるには、
(3-8)式から \(t\) を求め、それを(3-5)(3-6)式に代入することで、平板Bが距離 \(l\) 進んだときの、A、Bの速度\(v_A\)、\(v_B\)を求めることができます。
さらに、\(L\)を求めるには、(3-8)式から求めた \(t\) の値を(3-7)式に代入します。
(\(L\)を表す式には \(l\) が含まれることに注意しましょう。)
逆に、\(L\)が与えられて \(l\) を求める場合がありますが、このときには、(3-8)式を(3-7)式に代入して\(t\)を求め、(3-8)式に代入することになりますが、\(t\) を求めるために二次方程式を解くことになるため、こちらはめんどうな計算になります。
②力積と運動量の変化量の関係
時刻 \(t\) でのA、Bの速度をそれぞれ\(v_A\)、\(v_B\)として、
「運動量の変化量=力積」の式を表すと、
\begin{eqnarray} mv_A-mv_0&=&-\mu mg\times t \tag{3-9} \\
Mv_B-M\times 0&=&\mu mg\times t \tag{3-10}
\end{eqnarray}
となります。
(3-9)式の両辺を\(m\)で割り、(3-10)式の両辺を\(M\)で割り、式を変形すると、
\begin{eqnarray} v_A&=&v_0-\mu gt \tag{3-11} \\
v_B&=&\mu\frac{m}{M}gt \tag{3-12}
\end{eqnarray}
となり、これは(3-5)(3-6)式と一致します。
力積と運動量の変化の関係はもともと運動方程式から導かれたもので、Ⅰ章の(1-1)~(1-4)式の変形を具体的な例題に沿って再確認したことになります。
さて、(3-9)(3-10)式だけではこの問題を解くことはできません。
それは、時刻 \(t\) でBが \(l\) 進んだという条件を表す式がないからです。
ところで、時間が経つと、Aの速度は減り、Bの速度は増加するので、ある時刻でAとBの速度が同じになります。
これは、「AがBに対して静止した」と、表現することもできます。
(3-11)(3-12)式を用いて、\(v_A=v_B\)を計算すれば、このときの時刻を求めることができます。 そして、その時刻を(3-11)あるいは(3-12)式に代入すれば、そのときのAとBの速度を求めることができます。
\begin{eqnarray} v_0-\mu gt&=&\mu\frac{m}{M}gt \\
t\mu g\left(\frac{M+m}{M}\right)&=&v_0 \\
t&=&\frac{Mv_0}{\mu g(M+m)} \tag{3-11'} \\
\\
\\
v_B&=&\mu\frac{m}{M}gt \\
&=&\mu\frac{m}{M}g\frac{Mv_0}{\mu g(M+m)} \\
&=&\frac{mv_0}{M+m} \tag{3-12'}
\end{eqnarray}
③運動量保存則
ここで、図3-1をもう一度示します。
さて、AとBからなる系を考えた場合、AとBの水平方向の運動量の和は保存されます。
AとBには水平方向に動摩擦力がはたらいています。
AとBにはたらく動摩擦力の大きさは等しく、向きは逆向きです。つまり、AとBからなる系にとって、動摩擦力は内力であるため、運動量の和が保存されます。
式に表せば、
\begin{equation} mv_0+M\times 0=mv_A+Mv_B \tag{3-13} \end{equation}
となります。
この式は、(3-9)式と(3-10)式から \(\mu mgt\) を消去し、式を整理すれば得られます。
運動量保存則は、力積と運動量の変化量の関係から導かれますが、時刻 \(t\) を含まない表現になります。
さて、この(3-13)式だけでは、問題を解くことができません。
\(v_A\)と\(v_B\)の関係式は得られましたが、それぞれの値を求めるには条件がもうひとつ必要です。
その条件が、Bが \(l\) 進んだことなのですが、これを式に表すには運動方程式を利用する必要があります。
④力学的エネルギー保存則
AとBからなる系では、力学的エネルギーの和は保存されません。
AとBにはたらく動摩擦力は非保存力です。
動摩擦力は同じ大きさでAとBに逆向きにはたらきますが、動摩擦力がAにする仕事とBにする仕事の大きさが異なります。
\begin{eqnarray} 動摩擦力がAにする仕事は、&&-\mu mg(L+l) \\
動摩擦力がBにする仕事は、&&\mu mgl です。
\end{eqnarray}
非保存力の動摩擦力がAにする仕事とBにする仕事が相殺されれば、AとBの力学的エネルギーの和は保存されることになりますが、上に見るように相殺されません。つまり、動摩擦力はAとBからなる系に対して正味の仕事をすることになり、力学的エネルギーの和は保存されないことになります。
力学的エネルギー保存則はこの場合成り立ちませんが、次の仕事と運動エネルギーの変化量との関係は常に成り立ちます。
次にこれを見てみましょう。
⑤運動エネルギーと仕事の関係
運動方程式を使って、AとBの加速度が(3-3)(3-4)式と求められています。
Aは加速度\(-\mu g\)で\(L+l\)の距離進んで、速度が\(v_0\)から\(v_A\)まで変化しました。
同時に、Bは加速度\(\mu\frac{m}{M}g\)で \(l\) の距離進んで、速度が\(0\)から\(v_B\)まで変化しました。
これらのことを等加速度運動の式を使って式に表すと、
\begin{eqnarray} v_A^2-v_0^2&=&2(-\mu g)(L+l) \tag{3-14} \\
v_B^2-0^2&=&2\left(\mu\frac{m}{M}g\right)l \tag{3-15}
\end{eqnarray}
となります。
(3-14)式\(\times\frac{1}{2}m\)、および、 (3-15)式\(\times\frac{1}{2}M\)を計算すると、次のようになります。
\begin{eqnarray} \frac{1}{2}mv_A^2- \frac{1}{2}mv_0^2&=&-\mu mg(L+l) \tag{3-16} \\
\frac{1}{2}Mv_B^2-\frac{1}{2}M\times 0^2&=&\mu mgl \tag{3-17}
\end{eqnarray}
(3-16)(3-17)式の左辺はAとBそれぞれの運動エネルギーの変化量を示しています。
一方、右辺は④で考えたように摩擦力がそれぞれAとBにした仕事を表しています。
つまり、(3-16)(3-17)式は[運動エネルギーの変化量]=[された仕事]を表しています。
右辺の摩擦力がした仕事を足し合わせると、\(-\mu mgl\)と\(\mu mgl\)は相殺されますが、\(-\mu mgL\)が残ります。
これが摩擦力がAとBからなる系にした仕事で、力学的エネルギー(運動エネルギー)の和が保存されないことがわかります。
⑥まとめ
以上より、この例題を解くには運動方程式を利用するのが最も良いことがわかりました。
また、運動方程式が最も基本であることもわかりました。
以上の内容をもう一度ここに示しておきます。
上の表において、左列の式や力積と仕事の式では、力や加速度が時間や位置により変化しない場合の表現になっています。
これは、等加速度運動をもとにして、運動量や力学的エネルギー保存則を導いているためです。
しかし、「運動量の変化量=力積」や「運動エネルギーの変化量=仕事」は、等加速度運動以外の運動についても考えることができますから、力が時間や位置に依存する場合、[力]×[時間]や[力]×[変位]から力積や仕事を計算するのではなく、運動量の変化量や運動エネルギーの変化量からこれらの量を推し量ることができます。
Ⅳ.力積の例題
例題1
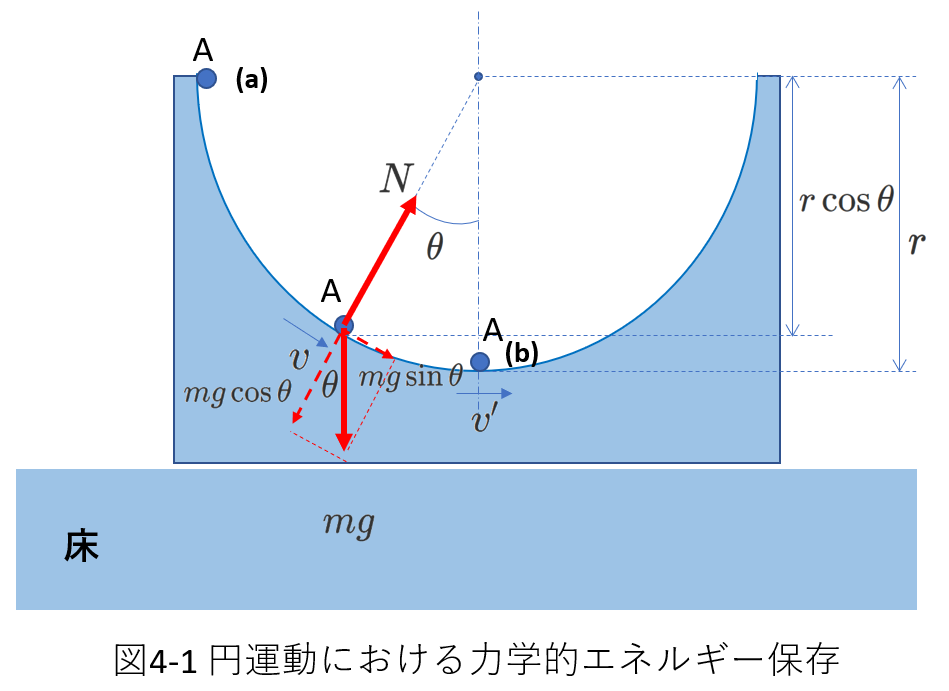
図4-1では、床の上に内面が円筒の台が乗っています。図はその断面を示しています。
質量\(m\)の物体Aを内面の上端(a)に置き、手を離したところ断面(半円)に沿って運動して(b)を通過しました。
物体Aが(a)の位置から(b)を通過する瞬間までにAが受けた力積を求めることにします。
Aが(a)の位置にあるときの運動量は\(0\)です。
(b)の位置では、Aの運動量の向きは水平右向きで、大きさは速さを\(v'\)として\(mv'\)です。
\(v'\)は力学的エネルギー保存から求めることができます。
図4-1に示したように、運動中のAにはたらく力は重力と垂直抗力です。
重力は保存力、垂直抗力はAの進行方向に垂直であるためAに対して仕事をしません。(つまり、運動エネルギーを変化させません。)このため、Aの力学的エネルギーは保存されます。
位置エネルギーの基準を(b)にとり、[(a)でのAの力学的エネルギー]=[(b)でのAの力学的エネルギ―」という式を立てます。すると、
\begin{eqnarray} \frac{1}{2}m\times 0^2+mgr&=&\frac{1}{2}mv'^2+mg\times 0 \tag{4-1} \\
\frac{1}{2}mv'^2&=&mgr \\
v'&=&\sqrt{2gr} \tag{4-2}
\end{eqnarray}
以上のことと(1-4)式とから、求める力積は、向きが水平方向右向きで大きさが\(m\sqrt{2gr}\)であることがわかります。
Aにはたらく力は、重力と垂直抗力です。
(a)から(b)に進む間にAが受ける力積は、このふたつの力によるものですから、
垂直抗力の鉛直成分による力積と重力による力積の和は\(0\)となることになります。
垂直抗力の水平成分による力積が\(m\sqrt{2gr}\)で表されることになります。
例題2
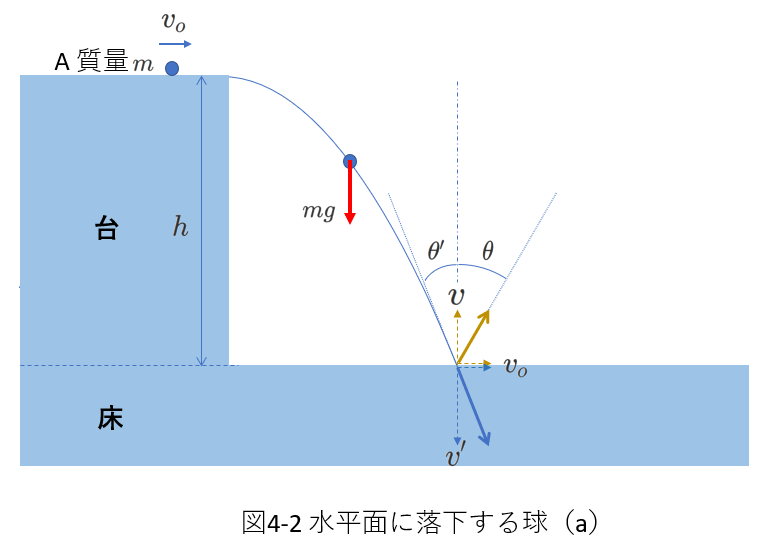
図4-2は、床上に固定された台の上から質量\(m\)の小球が落下するところを示しています。
台の高さは\(h\)、台上でAは水平右向きに速さ\(v_0\)、重力加速度は\(g\)、どこにも摩擦はないものとします。
Aは台を離れたのちに床に衝突してはね返ります。
Aと床の反発係数(はね返り係数)を\(e\)とします。
衝突時にAが床から受ける力積の大きさを求めましょう。
衝突時にAと床が及ぼし合う衝撃力の大きさもそれがはたらいている時間もわかりませんから、
Aの運動量の変化から力積を求めることになります。
衝突直前のAの速さは、\(v_0\)と力学的エネルギー保存則(または、運動方程式)から求めることができ、これより衝突直前のAの運動量が計算できます。衝突直後の速度は、反発係数(はね返り係数)の定義式から求めることができます。
ここで、小球Aについて衝突直前直後で運動量は保存されないことに注意しましょう。
A単独で考えた場合、衝突時の衝撃力は外力になります。
また、Aと床からなる系を考えた場合、床は動かないという設定ですから、床がAから衝撃を受けたときに床が動かないように衝撃につり合う力(これは外力)が与えられたと考えられるため、やはり運動量は保存されません。
床がAに及ぼす衝撃力の向きは、摩擦がありませんから、(床面に垂直で)鉛直上向きです。
衝突直前直後で水平方向には力ははたらかないのですから、衝突直前直後で速度の水平成分は変化しません。
したがって、反発係数(はね返り係数)の式を立てる場合は、床面の法線方向(この場合は鉛直方向)の速度成分を用いて立てることになります。
式を立てやすいように、衝突直前のAの速度の鉛直方向の成分の大きさを\(v'\)、衝突直後のAの速度の鉛直方向の成分の大きさを\(v\)とします。
速度の正の向きを上向きにとり、これらの文字を使って、反発係数(はね返り係数)の式を立てます。
\begin{eqnarray} e&=&-\frac{v-0}{-v'-0} \tag{4-3} \\
v&=&ev' \tag{4-4}
\end{eqnarray}
さて\(v'\)は、次の力学的エネルギー保存則から求めることができます。
左辺は台上のAの力学的エネルギー、右辺は衝突直前のAの力学的エネルギーで、位置エネルギーの基準を床面としています。
\begin{eqnarray} \frac{1}{2}mv_0^2+mgh&=&\frac{1}{2}mv'^2+\frac{1}{2}mv_0^2+mg\times 0 \tag{4-5} \\
\frac{1}{2}mv'^2&=&mgh \\
v'&=&\sqrt{2gh} \tag{4-6}
\end{eqnarray}
(4-5)式で、Aの運動エネルギーを求めるのに、速度の水平方向成分による項と鉛直方向成分による項の和を考えていることに注意しましょう。
衝突直前のAの速さを\(V'\)とすると、\(V'\)はその水平成分\(v_0\)と鉛直成分\(v\)を用いて、次のように表されます。
\begin{eqnarray} V'&=&\sqrt{v_0^2+v^2} \\
これより、V'^2&=&v_0^2+v^2 \\
両辺に\frac{1}{2}mを掛けて、\frac{1}{2}mV'^2&=&\frac{1}{2}mv_0^2+\frac{1}{2}mv^2 \tag{4-7}
\end{eqnarray}
(4-4)式と(4-6)式から、求める力積\(I\)は、鉛直上向きを正の向きとして、
\begin{eqnarray} I&=&mv-m(-v') \\
&=&mv'(e+1) \\
&=&m(e+1)\sqrt{2gh} \tag{4-8}
\end{eqnarray}
上の式では、\(-v'\)の負号に注意してください。
この例題では、力積の大きさを求めました。力積はベクトル量ですから、その点を確認しておきましょう。
運動量の変化量と力積\(\overrightarrow{I}\)の関係をベクトルで表すと、次のようになります。
\begin{equation} \overrightarrow{I}=m\overrightarrow{V}-m\overrightarrow{V'} \tag{4-9}
\end{equation}
ここで、\(\overrightarrow{V'}\)、\(\overrightarrow{V}\)はそれぞれ衝突直前と衝突直後のAの速度です。
(4-9)式は、力積の向きと運動量変化の向き(=速度の変化の向き)は同じであることを示しています。
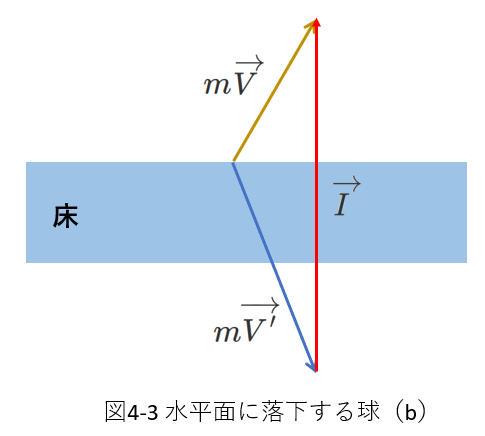
(4-9)式を表すベクトル図を描くと、\(m\overrightarrow{V}\)と\(m\overrightarrow{V'}\)の水平成分が等しいことに注意して、図4-3のようになります。
前述したように、この例題では速度の鉛直成分だけが変化します。
したがって、力積の方向も鉛直方向です。
力積の水平方向成分は\(0\)です。
また、
\begin{eqnarray} \tan\theta'&=&\frac{v_0}{v'} \\
\tan\theta&=&\frac{v_0}{v}=\frac{v_0}{ev'} \\
したがって、e&\neq&1ならば、\theta'\neq\theta
\end{eqnarray}
です。
なんとなく、\(\theta'=\theta\)と考えてしまうので注意が必要です。
例題3
次に、例題2で床が傾いている場合について考えます。
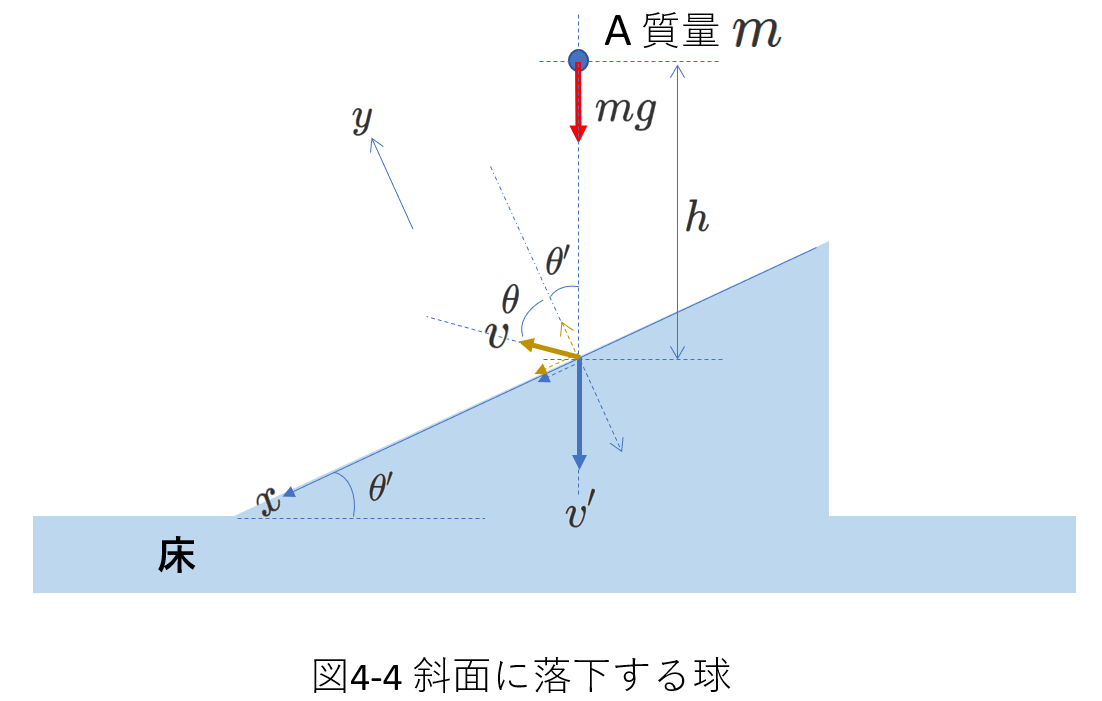
図4-4に示すように、水平面との角度が\(\theta'\)の固定された斜面があります。
今、質量\(m\)の小球Aを斜面の上方で静かに放しました。
Aは\(h\)の距離進んで斜面に衝突しました。
どこにも摩擦ははたらかないものとし、Aと斜面の反発係数(はね返り係数)を\(e\)とします。
このときにAが斜面から受ける力積の大きさと向きを求めます。
Aと斜面の間には摩擦ははたらかないので、衝突時の衝撃力の向きは、斜面に垂直に上向きです。
したがって、Aの衝突直前の速度、直後の速度を斜面に垂直(\(y\)方向)な成分と斜面方向(\(x\)方向)に分けて考えます。
衝突直前のAの速さを\(v'\)、衝突直後のAの速さを\(v\)とします。
衝突直後のAの速度の向きを\(y\)方向から角度\(\theta\)だけ傾いた向きであるとすると、それぞれの速度成分は、
\begin{eqnarray} 衝突直前 x方向&& v'\sin\theta' \\
y方向&& v'\cos\theta' \\
衝突直後 x方向&& v\sin\theta \\
y方向&& v\cos\theta
\end{eqnarray}
図4-4では、衝突直前のAの速度とその成分を青色で、衝突直後のAの速度とその成分を茶色で表しています。
衝撃力は斜面方向にははたらかないので\(v'\sin\theta'=v\sin\theta\)です。
(衝突の間には衝撃力以外に重力がはたらいていて、重力には斜面方向の成分があります。
ただし、重力は衝突の衝撃力よりもずっと小さく、その効果が無視できるものとして、衝突を考えるときには重力の効果を考えなくても良いとします。運動量保存の法則が近似的に成り立つ場合と同じ論理です。)
また、反発係数(はね返り係数)は斜面に垂直な方向(\(y\)方向)の成分で考えます。
したがって、
\begin{eqnarray} e=-\frac{v\cos\theta-0}{-v'\cos\theta'-0} \tag{4-10} \\
v\cos\theta=ev'\cos\theta'
\end{eqnarray}
以上より、求める力積の大きさ\(I'\)は、
\begin{eqnarray} I'&=&mv\cos\theta-m(-v'\cos\theta') \\
&=&mev'\cos\theta'+mv'\cos\theta' \\
&=&mv'(e+1)\cos\theta' \\
&=&m(e+1)\sqrt{2gh}\cos\theta' \ (4-6)式より、v'=\sqrt{2gh}
\end{eqnarray}
となります。\(\theta'=0\)ならば例題2と同じ条件となり、(4-8)式と同じになります。
ここで、\(v\cos\theta\)をまとめて一つの未知数として取り扱っていることに注意してください。
\(I'\)を求めるために必要なのは\(v\cos\theta\)なわけですから、\(v\)と\(\theta\)の両方を求める必要はありません。
したがって、最初から衝突直後のAの速度の斜面に垂直な方向の成分(\(v\cos\theta\))を\(x\)と置いて、これを求める方がわかりやすく、ミスも少ないでしょう。
例題4
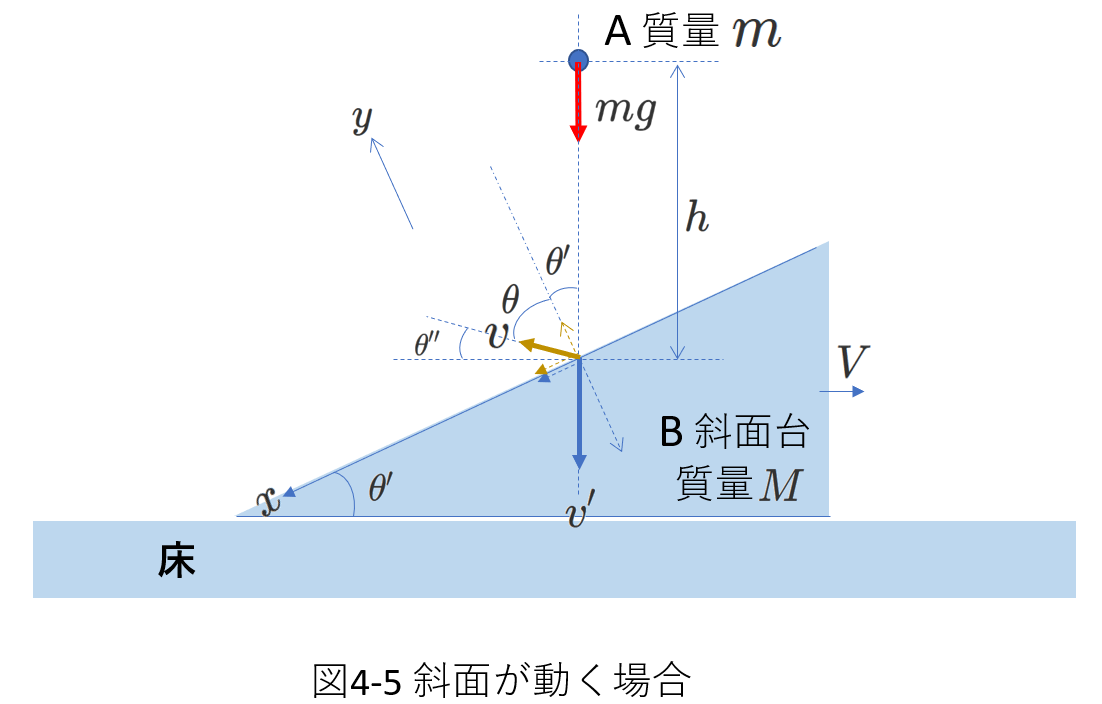
前出の図4-4において、斜面台が床から切り離されていて、斜面台が自由に動く場合について考えます。
それを図4-5に示します。
なめらかな床の上に自由に動く斜面台Bが乗っています。
斜面の角度は水平面から\(\theta'\)です。
静止している斜面台の上方で静かに放した小球Aが\(h\)の距離落下して斜面台に衝突しました。
Aは斜面ではね返り、Bは右向きに動きました。
Aの質量は\(m\)、Bの質量は\(M\)です。また、摩擦はどこにもないものとします。
今までと同じように、衝突によりAが受けた力積を求めます。
問題を考えやすくするため、衝突直前のAの速さを\(v'\)、衝突直後のAとBの速さをそれぞれ\(v\)、\(V\)とします。
また、図に示すように、衝突直後のAの速度の向きと、斜面に垂直な方向との角度を\(\theta\)、水平方向との角度を\(\theta''\)とします。
例題3との違いは、斜面台が固定されていないで、自由に動くことです。
Aにはたらく力積を求めるためには、Aの運動量の変化(すなわち、衝突直前と直後のAの速さ)を求める必要があります。
衝突直前のAの速さは力学的エネルギー保存から求めた(4-6)式の値が使えます。
また、衝突時の衝撃力の向きは(例題3と同じように)、斜面に垂直です。
衝撃力は斜面方向の成分がないので、衝突前のAの速度の斜面方向成分と衝突後のAの速度の斜面方向成分は等しいはずです。
したがって、
\begin{equation} v\sin\theta=v'\sin\theta' \tag{4-11} \end{equation}
難しいのは衝突直後のAの速さです。台も\(V\)の速さで動くことを考慮しなければなりません。
衝突ですから、運動量の保存が成り立つかどうかを検討します。
AとBにはたらく衝撃力はAとBからなる系については内力です。
Aには重力がはたらいていてこれは外力となりますが、例題3でも考えたように、衝撃力に比べて非常に小さいと考えられるため、無視することができます。
BがAから受けた力(力積)は、水平方向成分も鉛直方向成分も持ちますから、Bは水平方向にも鉛直方向にも動くはずです。
しかし、床があるためBは鉛直方向には動きません。
これは、床からBが鉛直方向には動かないような力(力積)がはたらいていると考えることができ、これは外力となります。
以上から、AとBからなる系の運動量の鉛直方向成分は保存されず、水平方向成分は保存されることがわかります。
上では、2組の方向が出てきていることに注意してください。
反発係数を考える場合については、斜面方向とこれに垂直な方向について考え、反発係数の式は斜面に垂直な方向について立式します。運動量保存については、水平方向と鉛直方向について考え、運動量保存の式は水平方向について立式します。
2組の方向を扱うことを意識し、混同しないようにします。
反発係数の式を立てると、
\begin{eqnarray} e=-\frac{v\cos\theta-(-V\sin\theta')}{(-v'\cos\theta')-0} \tag{4-12} \\
これより、ev'\cos\theta'=(v\cos\theta)+V\sin\theta' \tag{4-13}
\end{eqnarray}
AとBからなる系の衝突直前直後の運動量の水平成分の保存の式を立てると、
衝突直前には、系の運動量の水平成分は\(0\)ですから、
\begin{eqnarray} 0=MV-mv\cos\theta'' \tag{4-14} \\
\theta''=\frac{\pi}{2}-(\theta'+\theta) \\
したがって、\cos\theta''&=&\cos\left(\frac{\pi}{2}-(\theta'+\theta)\right) \\
&=&\cos\frac{\pi}{2}\cos(\theta'+\theta)+\sin\frac{\pi}{2}\sin(\theta'+\theta) \\
&=&\sin(\theta'+\theta) \\
&=&\sin\theta' \cos\theta+\cos\theta' \sin\theta \\
これより、(4-13)式は、0&=&MV-mv(\sin\theta' \cos\theta+\cos\theta' \sin\theta) \\
&=&MV-m(v\cos\theta)\sin\theta'-m(v\sin\theta)\cos\theta' \tag{4-15}
\end{eqnarray}
(4-15)式の\(v\cos\theta\)は衝突後のAの速度\(v\)の斜面に垂直な方向の成分を表していて、(4-11)式からこれは\(v'\sin\theta'\)に等しいです。これより、\(v\cos\theta \sin\theta'\)は\(v\cos\theta\)の水平方向の成分を表しています。
(4-15)式の\(v\sin\theta\)は衝突後のAの速度\(v\)の斜面に沿った方向の成分を、したがって、\(v\sin\theta \cos\theta'\)は\(v\sin\theta\)の水平方向成分を表します。
したがって、ふたつ合わせた\(m(v\cos\theta)\sin\theta'+m(v\sin\theta)\cos\theta'\)は、衝突後のAの速度\(v\)の水平方向成分を表していることになり、(4-15)式が確かに運動量の水平成分の保存を表していることが再確認できました。
\(v\cos\theta\)が力積を計算するうえで重要な項なので、これをあらためて\(x\)と置き、\(v\sin\theta\)を\(v'\sin\theta'\)で置き換えて、(4-13)(4-15)式を書き改めると、
\begin{eqnarray} ev'\cos\theta'&=&x+V\sin\theta' \tag{4-16} \\
MV&=&mx\sin\theta'+mv'\sin\theta' \cos\theta' \tag{4-17}
\end{eqnarray}
(4-16)(4-17)式で、未知数は\(x\)と\(V\)です。
\(\theta'\)は既知ですし、\(v'\)は\(h\)と力学的エネルギー保存から求めることができます。
\(x\)が必要なので、(4-16)式から\(V\)を求め、これを(4-17)式に代入して\(x\)を求めます。
力積を求める上では、\(x\)だけ求めればよいのですが、ここでは\(V\)も求めておきます。
\begin{eqnarray} (4-16)式から、V&=&\frac{ev'\cos\theta'-x}{\sin\theta'} \\
これを(4-17)式に代入して、&&両辺に\sin\theta'を掛けて、 \\
M(ev'\cos\theta'-x)&=&mx\sin^2\theta'+mv'\sin^2\theta' \cos\theta' \\
(m\sin^2\theta'+M)x&=&Mev'\cos\theta'-mv'\sin^2\theta'\cos\theta' \\
x&=&\frac{(Me-m\sin^2\theta')v'\cos\theta'}{M+m\sin^2\theta'} \tag{4-18} \\
V&=&\frac{ev'\cos\theta'-x}{\sin\theta'} \\
&=&\frac{mv'(e+1)\sin\theta' \cos\theta'}{M+m\sin^2\theta'} \tag{4-19}
\end{eqnarray}
求めるのは、衝突によりAが受けた力積の大きさ\(I\)です。
先述したように、斜面台がAに及ぼした力積の向きは斜面に垂直上向きですから、衝突によるAの運動量の斜面に垂直な方向の成分の変化が\(I\)に等しいと考えることができます。
\begin{eqnarray} I&=&mv\cos\theta-m(-v'\cos\theta') \\
&=&mx+mv'\cos\theta' \\
&=&m\frac{(Me-m\sin^2\theta')v'\cos\theta'}{M+m\sin^2\theta'}+mv'\cos\theta' \\
&=&\frac{mMv'(e+1)\cos\theta'}{M+m\sin^2\theta'} \tag{4-20}
\end{eqnarray}
ここで、\(v'\)は(4-6)式で与えられます。
注)上の解法では、(4-14)~(4-15)式で式の変形や考察にわずらわしいところがありました。
これを解消するには、最初から衝突後のAの速度の斜面に垂直な成分を未知数\(x\)として(4-12)(4-14)式を立てるのが良いです。
衝突後のAの速度の斜面方向成分は\(v'\cos\theta'\)を用いることができ、これにより、\(\theta''\)を用いる必要がなくなります。
この例題について、もう2点考察します。
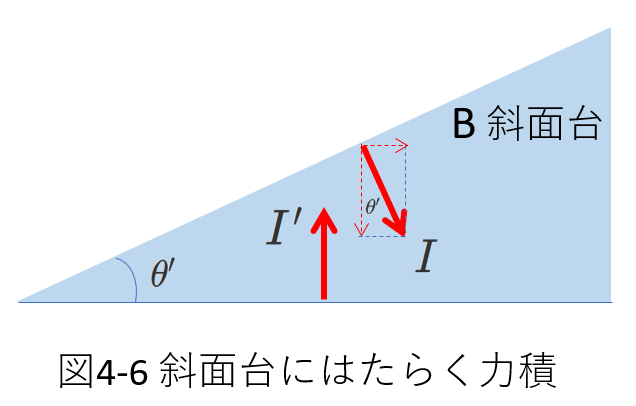
①台が受ける力積について
衝突時に斜面台にはたらく力積を図示すると、右図4-6のようになります。
Aから斜面に垂直に\(I\)の大きさの力積を受けます。
また、床から\(I'\)の大きさの力積を受けます。
斜面台の運動量の鉛直方向成分は衝突前後で変化しないのですから、\(I\)の鉛直成分と\(I'\)は相殺されます。
注)斜面台には重力\(Mg\)もはたらいているので、衝突の間にこれに起因する力積も存在します。
ただし、重力は衝撃力に比べて非常に小さく、したがって、力積も小さいことと、この力積は鉛直方向にはたらくため、以下の考察の結果の(4-21)式には影響を与えないため、図4-6では重力\(Mg\)による力積を省略しています。
また、重力による力積も相殺するように\(I'\)が決まると考えることもできます。
水平方向には、\(I\sin\theta'\)の力積がはたらき、斜面台の運動量の水平成分を\(0\)から\(MV\)に変化させます。このことから、次の関係が成り立つはずです。
\begin{equation} I\sin\theta'=MV-0 \tag{4-21} \end{equation}
この考えが正しいことを、上の式の\(V\)に(4-19)式を代入して\(I\)を求め、(4-20)式と等しくなることから確認します。
\begin{eqnarray} I\sin\theta'&=&MV-0 \\
&=&\frac{Mmv'\sin\theta' \cos\theta'(e+1)}{M+m\sin^2\theta'} \\
I&=&\frac{mMv'\cos\theta'(e+1)}{M+m\sin^2\theta'}
\end{eqnarray}
(4-20)に等しい結果が得られました。
②力学的エネルギー保存について
衝突が弾性衝突の場合(\(e=1\))のとき、衝突の直前と直後でAとBの力学的エネルギーの和が保存されることを確認します。
注)弾性衝突以外の衝突(\(e\neq 1\))の場合には、力学的エネルギーは保存されません。
また、A単独で考えた場合、衝突の衝撃力は保存力でないこと、衝撃力はAに対して仕事をしていることから、
A単独では力学的エネルギーは保存されません。
Aにはたらく力は重力とBからの衝突の衝撃力です。また、Bにはたらく力はAからの衝突の衝撃力と重力と床からの抗力です。
重力は保存力、Bが床から受ける抗力は斜面台に対して仕事をしていないこと、衝突は弾性衝突であることから、AとBからなる系について、力学的エネルギーが保存されると考えられます。
この例題について、衝突の直前直後でAとBからなる系の力学的エネルギー保存が成立することを数式で確認します。
衝突の直前直後でAとBの位置の変化はありませんから、運動エネルギーのみ検討します。
力学的エネルギー(運動エネルギー)が保存されるとすれば、それは、
[衝突直後のAの速度の斜面に垂直な成分に対する運動エネルギー]+[衝突直後のAの速度の斜面に沿った成分に対する運動エネルギー]+[衝突直後のBの運動エネルギー]=[衝突直前のAの速度の斜面に垂直な成分に対する運動エネルギー]+[衝突直前の速度の斜面に沿った成分に対する運動エネルギー]
と表されます。数式で表せば、
\begin{eqnarray} \frac{1}{2}m(v\cos\theta)^2+\frac{1}{2}m(v\sin\theta)^2+\frac{1}{2}MV^2&=&\frac{1}{2}m(v'\cos\theta')^2+\frac{1}{2}m(v'\sin\theta')^2 \\
(4-11)式を用いれば、左辺第2項と右辺第2項は消去されて、 \\
\frac{1}{2}m(v\cos\theta)^2+\frac{1}{2}MV^2&=&\frac{1}{2}m(v'\cos\theta')^2 \tag{4-22}
\end{eqnarray}
今、\(e=1\)の場合を検討しているので、(4-18)(4-19)式は次のようになります。
\begin{eqnarray} v\cos\theta&=&\frac{(M-m\sin^2\theta')v'\cos\theta'}{M+m\sin^2\theta'} \tag{4-23} \\
V&=&\frac{2mv'\sin\theta' \cos\theta'}{M+m\sin^2\theta'} \tag{4-24}
\end{eqnarray}
(4-23)(4-24)式を(4-22)式の左辺に代入し、(4-22)式の右辺が導かれることを示します。
これができれば、(4-22)式、すなわち、衝突直前と直後で力学的エネルギー(運動エネルギー)が保存されることが示されることになります。
\begin{eqnarray} \frac{1}{2}m(v\cos\theta)^2+\frac{1}{2}MV^2
=\frac{1}{2}m\left(\frac{(M-m\sin^2\theta')v'\cos\theta'}{M+m\sin^2\theta'}\right)^2+\frac{1}{2}M\left(\frac{2mv'\sin\theta' \cos\theta'}{M+m\sin^2\theta'}\right)^2 \\
=\frac{m(M^2v'^2\cos^2\theta'+m^2v'^2\sin^4\theta' \cos^2\theta'-2mMv'^2\sin^2\theta' \cos^2\theta')+4Mm^2v'^2\cos^2\theta' \sin^2\theta'}{2(M+m\sin^2\theta')^2} \\
=\frac{mM^2v'^2\cos^2\theta'+m^3v'^2\sin^4\theta' \cos^2\theta'+2m^2Mv'^2\sin^2\theta' \cos^2\theta'}{2(M+m\sin^2\theta')^2} \\
=\frac{mv'^2\cos^2\theta'(M^2+m^2\sin^4\theta'+2mM\sin^2\theta'}{2(M+m\sin^2\theta')^2} \\
=\frac{mv'^2\cos^2\theta'(M+m\sin^2\theta')^2}{2(M+m\sin^2\theta')^2} \\
=\frac{1}{2}mv'\cos^2\theta'
\end{eqnarray}
証明が終わりました。
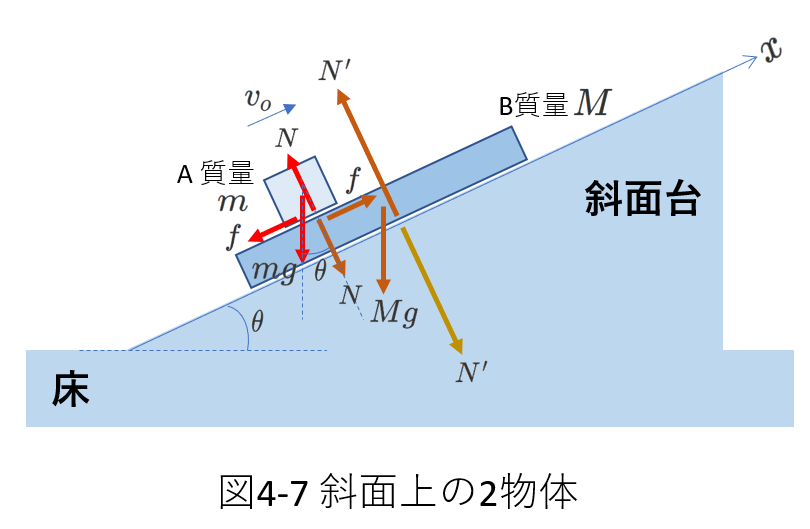
例題5
右図4-7のように床に固定された斜面台の上に質量\(M\)の板状の物体Bが、さらにその上に質量\(m\)の箱状の物体Aが乗っています。AとBの間には摩擦力(動摩擦係数を\(\mu\))がはたらきますが、Bと斜面台の間には摩擦はないものとします。斜面に沿って\(x\)軸を上向きを正として考えます。
A,Bは静止した状態で、\(t=0\)でAに初速\(v_0\)を\(x\)軸の正の向きに与えます。
これにより、AとBが上向きに運動を始めます。
Aの速さは次第に小さくなり、Bの速さは次第に大きくなります。
そして、ある時刻でAとBの速度が同じになります。
その時刻\(t'\)とそのときのAとBの速さ\(V\)を求めます。
AもBも斜面に沿って(\(x\)軸に沿って)運動するので、この向きについて式を立てます。
動摩擦力の大きさを\(f\)とし、速度、力の正の向きを\(+x\)向きとします。重力も動摩擦力\(f\)も一定(時間依存性がない)ですから、
\begin{eqnarray} Aについて: mV-mv_0=(-f-mg\sin\theta)t' \tag{4-25} \\
Bについて: MV-M\times 0=(f-Mg\sin\theta)t' \tag{4-26}
\end{eqnarray}
Aにはたらく力の斜面に垂直な方向の力がつりあっていることから、\(N=mg\cos\theta\)ですから、動摩擦力の大きさは\(f=\mu mg\cos\theta\)です。
(4-25)(4-26)式で未知数は\(V\)と\(t'\)のふたつですから、\(V\)を消去して\(t'\)を求めることにします。
(4-25)×M-(4-26)×mを計算すると、
\begin{eqnarray} M(mV-mv_0)-mMV&=&t'\{M(-f-mg\sin\theta)-m(f-Mg\sin\theta)\} \\
-Mmv_0&=&t'(-Mf-Mmg\sin\theta-mf+Mmg\sin\theta) \\
Mmv_0&=&t'(M+m)f \\
t'&=&\frac{Mmv_0}{(M+m)f}=\frac{Mmv_0}{(M+m)\mu mg\cos\theta}=\frac{Mv_0}{(M+m)\mu g\cos\theta} \tag{4-27}
\end{eqnarray}
\(V\)を求めるには、(4-26)式に(4-27)式の\(t'\)を代入して、
\begin{eqnarray} MV&=&(\mu mg\cos\theta-Mg\sin\theta)\frac{Mv_0}{(M+m)\mu g\cos\theta} \\
V&=&\frac{v_0(\mu m\cos\theta-M\sin\theta)}{\mu(M+m)\cos\theta} \tag{4-28}
\end{eqnarray}
注)この例題では、Aに\(v_0\)を与えた直後のAとBの運動量の和と、AとBの速さが\(V\)になったときのAとBの運動量の和は等しくありません。
すなわち、AとBからなる系で運動量は保存されません。AとBには重力がはたらいていますが、
これはAとBからなる系に対して外力となっているからです。
ところで、(4-27)(4-28)式に大きな間違いがないことを簡単に検証しておきます。
\(v_0=0\)の場合を考えると、\(t'=0、V=0\)となり、これは合理的な結果です。
次に\(\theta=0\)の場合の(4-27)(4-28)式を考えます。
このときの\(t'\)と\(V\)を\(t'_s\)、\(V_s\)とすると、
\begin{eqnarray} t'_s&=&\frac{Mv_0}{\mu g(M+m)} \\
V_s&=&\frac{mv_0}{M+m}
\end{eqnarray}
これらの式は、「Ⅲ.運動方程式・力積・仕事」の章の「②力積と運動量変化量の関係」の(3-11’)(3-12’)式と一致します。Ⅲでは、水平面上(すなわち、\(\theta=0\))での2物体の運動を扱っており、これらも合理的な結果となり、矛盾がないことがわかります。
運動方程式がすべての基本ですから、この問題も運動方程式を使って解けます。
図4-7を参照すれば、AとBの加速度をそれぞれ、\(a\)、\(A\)として、運動方程式は次のようになります。
\begin{eqnarray} A:ma&=&-f-mg\sin\theta \tag{4-29} \\
B:MA&=&f-Mg\sin\theta \tag{4-30} \\
これより、&& \\
a&=&-\mu g\cos\theta-g\sin\theta \tag{4-31} \\
A&=&\mu\frac{m}{M}g\cos\theta-g\sin\theta \tag{4-32}
\end{eqnarray}
\(t'\)後の速さ\(V\)は、それぞれの加速度を使って次のように表されます。
\begin{eqnarray} V&=&v_0+\left(-\mu g\cos\theta-g\sin\theta\right)t' \\
V&=&0+\left(\mu\frac{m}{M}g\cos\theta-g\sin\theta\right)t'
\end{eqnarray}
これより、
\begin{eqnarray}
v_0+\left(-\mu g\cos\theta-g\sin\theta\right)t'&=&\left(\mu\frac{m}{M}g\cos\theta-g\sin\theta\right)t' \\
v_0&=&\left(\mu\frac{m}{M}g\cos\theta-g\sin\theta+\mu g\cos\theta+g\sin\theta\right )t' \\
v_0&=&\mu g\cos\theta \left(\frac{m}{M}+1\right)t' \\
t'&=&\frac{Mv_0}{\mu g(M+m)\cos\theta}
\end{eqnarray}
(4-27)式と一致しました。
AとBがともに\(V\)になったとき、Bから見ればAは静止しているように見えます。
そこで、Bから見たAの運動を考えて\(t'\)を求めてみます。
Bから見てAにはたらく力は、
\begin{equation} (-f-mg\sin\theta)+(-mA) \tag{4-33} \end{equation}
この式の2番目の括弧はAにはたらく慣性力を表しています。
Bから見たAの速さは、\(v_0\)から\(0\)に変化するので、
運動量の変化と力積の関係を表すと、
\begin{eqnarray} m\times 0-mv_0&=&\{-f-mg\sin\theta-\frac{m}{M}(f-Mg\sin\theta)\}t' \\
&=&-f\left(1+\frac{m}{M}\right)t' \\
t'&=&\frac{mMv_0}{(M+m)f} \\
&=&\frac{Mv_0}{(M+m)\mu g\cos\theta}
\end{eqnarray}
(4-27)式と一致しました。
注)運動量の変化量と力積の関係は、上記のように相対速度と慣性力を考えても立式できますが、
運動量保存則を相対速度で表すことはできません。
運動量保存の式を立てる場合は、必ず着目している系の外側から観察した速度を用いて式を立てます。
例えば、例題5で、Bから見たAとBの相対速度を使って次のような式を立てるのは誤りです。
\begin{equation} mv_0+M\times 0=m\times 0+M\times 0 \end{equation}
相対速度を使った場合、Bの相対的な速さが衝突前も衝突後も\(0\)となってしまいますから、
誤りであることはすぐにわかりますが、試験で緊張している場合には気づかない場合があるので注意しましょう。
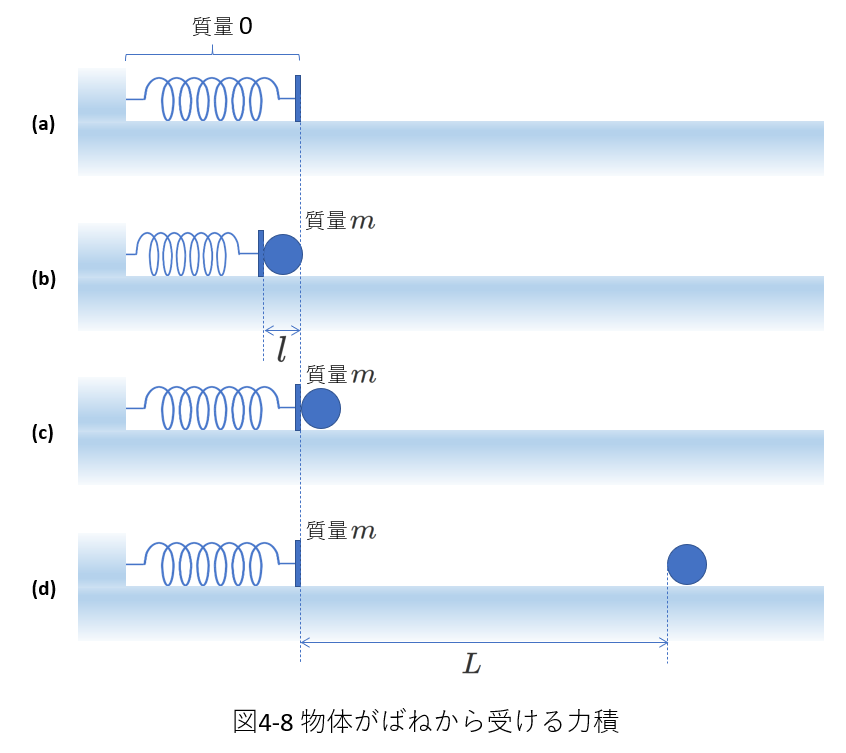
例題6
右図4-8(a)のように、床の上にばねが水平に置かれ、ばねの左端は壁に固定されています。
次に(b)のように、質量\(m\)の球状の物体をばねの右端に接触させたまま、ばねを長さ \(l\) だけ縮めます。
ばねの右端には物体を押し出すための板がついていますが、板を含めたばねの質量は\(0\)とします。
ばねを \(l\) だけ縮めて、物体を放したところ、物体はばねに押し出されて右に動き始めました。
物体と床の間には摩擦係数\(\mu\)の動摩擦力がはたらいていて、ばねの自然長の位置から\(L\)だけ離れたところで物体は静止しました。
物体が放されてから、(\(l+L\))の距離を移動する時間が\(t_0\)であったとき、ばねが物体に与えた力積を考えます。
どう考えたらよいでしょう。
ばねが物体に与える力積を計算しようとしても、ばねの弾性力が一定ではないので、単純な[力の大きさ]×[時間]では計算できそうもありません。
しかも、ばねが自然長に戻る間にも物体には動摩擦力がはたらいていて、運動を複雑にしています。
しかし、運動が複雑な場合の力積を求めるには、物体の運動量変化に着目するのが正攻法です。
もうひとつ着目する点は、物体には、ばねの弾性力と動摩擦力のふたつの力が働いていることです。
つまり、物体は、弾性力によるものと動摩擦力によるものの2つの力積を受けます。
このうち、動摩擦力は常に一定の大きさですから、力がはたらいている時間さえわかれば、「動摩擦力による力積」は計算できます。
水平右向きを正とすれば、重力加速度を\(g\)として、動摩擦力から受ける力積は、\(-\mu mgt_0\)です。
ばねの弾性力から受ける力積を\(I\)とすると、物体は(\(I-\mu mgt_0\))の力積を受けて、運動量が\(m\cdot 0\)から\(m\cdot 0\)に変化するわけですから、
\begin{eqnarray} m\cdot 0-m\cdot 0&=&I-\mu mgt_0 \tag{4-34} \\
I&=&\mu mgt_0
\end{eqnarray}
[力積]=[運動量の変化]を理解するとともに、「物体の運動量が\(m\cdot 0\)から\(m\cdot 0\)に変化する」という捉え方も覚えておきましょう。
この問題に、[仕事]=[運動エネルギーの変化] (4-35) を適用して何がわかるかを考えます。
物体は、ばねの弾性力と動摩擦力から仕事を受けます。
ばねが物体にした仕事は、ばね定数を\(k\)として、\(\frac{1}{2}kl^2\)です。
(ばねが物体に与えた「力積」は簡単な式に表すことはできなかったけれど、ばねが物体に与えた「仕事」は式で表せます。)
そして、動摩擦力が物体にした仕事は、\(-\mu mg(l+L)\)です。
運動エネルギ―の変化は、\(0\)から\(0\)です。
式に表すと、
\begin{equation} \frac{1}{2}m\cdot0^2-\frac{1}{2}m\cdot0^2=\frac{1}{2}kl^2-\mu mg(l+L) \tag{4-36} \end{equation}
となります。
(4-36)式から、\(L\)を \(l\) で表すことがきるということがわかります。
\(L\)を計算してみます。
\begin{eqnarray} 0&=&\frac{1}{2}kl^2-\mu mg(l+L) \\
\mu mgL&=&\frac{1}{2}kl^2-\mu mgl \\
L&=&\frac{kl^2}{2\mu mg}-l \\
&=&\left(\frac{kl}{2\mu mg}-1\right)l \tag{4-37}
\end{eqnarray}
(4-37)式の妥当性を検討してみます。
括弧内の分子\(kl\)も、分母\(\mu mg\)も力を表していて、括弧内は無名数(単位がつかない)となります。
したがって、左辺も右辺もともに長さの単位を持つことが確認できますから、大きな計算ミスはなさそうです。
(4-37)式の括弧内が\(0\)になると\(L=0\)となり、ばねが自然長に戻ったところで物体が静止します。
この条件は、
\begin{equation} \mu mg=\frac{1}{2}kl \tag{4-38} \end{equation}
です。
右辺は、物体を放す瞬間のばねの弾性力\(kl\)と自然長に戻ったときの弾性力の大きさ\(0\)の平均のようなもので、これが動摩擦力の大きさに等しいというわけで、それらしい結果となっています。。
(4-35)式は次のように書き直すことができます。
[物体が非保存力から受けた仕事]=[力学的エネルギーの変化] (4-39)
(4-39)式に沿って立式します。
ばねの弾性力は保存力、動摩擦力は非保存力ですから、
\begin{equation} \left(\frac{1}{2}m\cdot 0^2\right)-\left(\frac{1}{2}m\cdot 0^2+\frac{1}{2}kl^2\right)=-\mu mg(l+L) \tag{4-40} \end{equation}
(4-40)式は(4-36)式と同じものとなります。
関連ページ
- 作図
- 物理の問題を解く場合、図を描くことは必須と言えます。図を活用することで、考察が進み、その結果ミスを減らすことができます。図を活用する場合の注意点を説明しています。
- 運動方程式
- 物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。
- モーメントの考え方
- 力のモーメントについて、基本的注意事項のいくつかを説明しています。
- 運動量保存則を使う問題
- 運動量保存則は、力学でも最も重要な概念のひとつです。運動量が保存される場合と保存されない場合について説明し、例題を掲げました。
- 張力
- 糸につながれたおもりの運動では、糸の張力を考慮します。張力を考える場合のヒントを説明しています。
- 運動エネルギーと仕事の関係
- 運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。
- 力学的エネルギー保存則を考える
- 力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。
- 単振動
- 単振動に関する問題を解くときに必要な知識について説明をしています。
- 円運動
- 円運動を考えるには、向心力を用いて運動方程式を立てるか、遠心力で力のつりあいを考えます。円運動の問題は難しく感じますが、出題のパターンは多くありません。
- 二体問題 Ⅰ
- 互いに力を及ぼし合う二つの物体の動きを考えます。
.png)