物理の大学入試問題を解く

トップページ ＞ 力学 ＞ 運動量保存則を使う問題

　運動量保存則は教科書で次のように説明されています。
「外力による力積が加わらないとき、物体系全体の運動量の和は一定に保たれる。」
つまり、内力だけが働いている場合は、運動量保存則が成り立ちます。

 

　内力とは、作用・反作用が生じる運動で、垂直抗力、摩擦力、抵抗力などです。
いずれも、２つの物体の接触で生じる力です。

 

　運動量保存則では、「その前」と「その後」（衝突の場合は、「衝突直前」と「衝突直後」）の状態さえわかれば問題は解決します。つまり、その間（衝突）について考える必要がありません。運動量保存則は、力学的エネルギー保存則と同じようにたいへん強力なツールです。

（１）運動方程式から運動量保存則まで

 

　運動方程式は、
\begin{equation} m\alpha=F \end{equation}
ここで、\(\alpha=\frac{\Delta v}{\Delta t}\) を代入して変形すると、
\begin{equation} m\Delta v=F\Delta t \end{equation}
時刻\(t_1\)から\(t_2\)の間に速度が\(v_1\)から\(v_2\)に変化したとすると、

これが、「運動量と力積の関係」です。

 

 

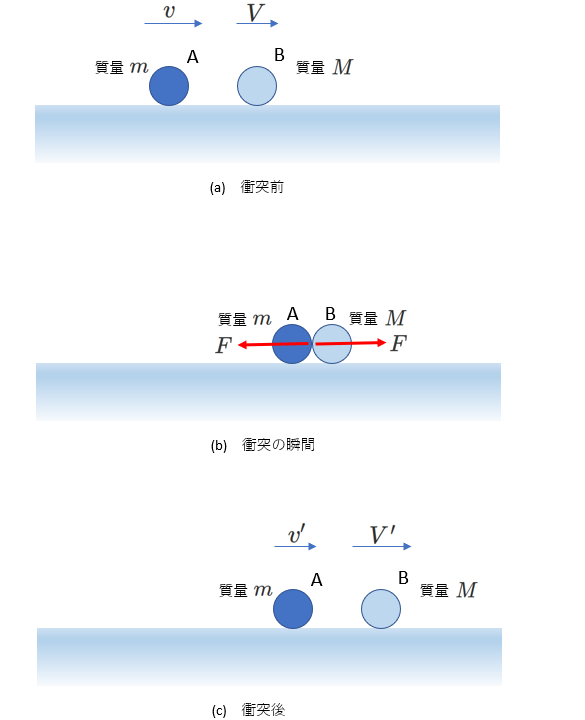
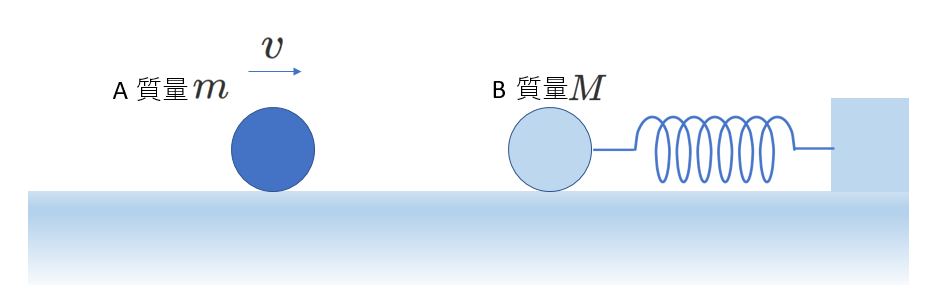
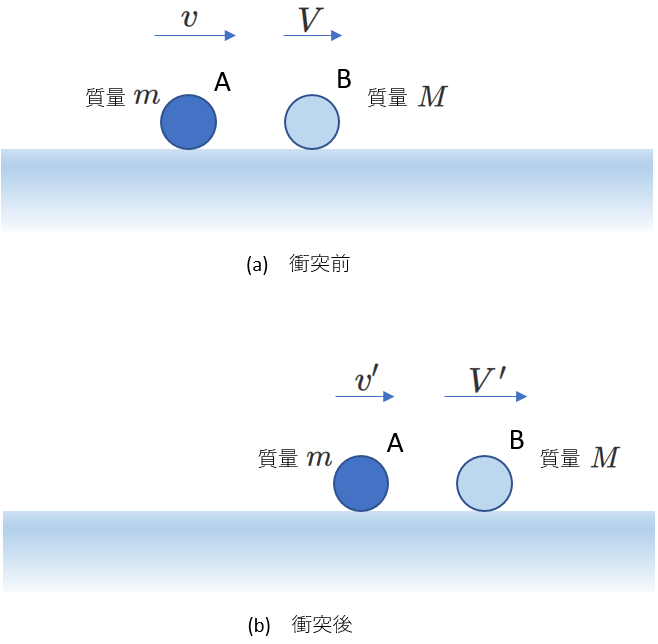
　質量が\(m\)の物体Aと\(M\)の物体Bの衝突を考えます。
　　　衝突直前のAの速度を\(v\)、Bの速度を\(V\)、
　　　衝突直後のAの速度を\(v'\)、Bの速度を\(V'\)とします。
　　　右図(b)に2つの物体の衝突の瞬間を示します。

 

　物体Bは、物体Aから\(F\)という力を受けます。
\(F\)が\(\Delta t\)の間作用したとすると、力積は、\(F\Delta t\)で、
(1)式の「運動量と力積の関係」から、
\begin{equation} MV'-MV=F\Delta t \tag{2-2} \end{equation}

 

　作用反作用の法則から、物体Aは、物体Bから\(-F\)（大きさが\(F\)で、向きが左向き）の力を受けます。
「運動量と力積の関係」から、
\begin{equation} mv'-mv=-F\Delta t \tag{2-3} \end{equation}
となります。

 

さて、(2-2)式と(2-3)式から、\(F\Delta t\)を消去して、
\begin{equation} MV'-MV= -(mv'-mv)　\end{equation}
左辺に衝突後の項を集め、右辺に衝突前の項を集めると、
\begin{equation} mv'+MV'=mv+MV　\tag{2-4}　\end{equation}

 

　このように、運動方程式から運動量保存則が導かれました。
この\(F\)と\(-F\)のように、ふたつの物体にそれぞれはたらく、大きさが同じで向きが逆の力が内力です。

 

　衝突の瞬間に、\(F\)と\(-F\)以外の力（外力）が働いていれば、それによっても物体の速度が変化しますから、
運動量保存則が成立しません。

 

（２）ベクトル量

 

さて、力積も運動量もベクトル量です。
それを意識して、(2-1)式と(2-4)式を書き直すと、
\begin{equation}
m\overrightarrow{v_2}-m\overrightarrow{v_1}=\overrightarrow{F}\Delta t \tag{2-5}
\end{equation}
\begin{equation}
m\overrightarrow{v'}+M\overrightarrow{V'}=m\overrightarrow{v}+M\overrightarrow{V} \tag{2-6}
\end{equation}

 

　出題される多くの問題は、1次元の衝突なので、(2-1)式と(2-4)式で十分ですが、
時々、2次元の衝突の問題が出題されます。
このときには、(2-5)式と(2-6)式を使います。
具体的には、ベクトル図を使って計算するか、成分に分けて計算します。

 

（３）観察者

 

もうひとつ大切なことは、
運動量保存則を使うときは、ふたつの物体からなる系の外から観察します。
念のため、
上の図で、物体Bの上の人が物体Aを観察する場合を考えてみましょう。
衝突前のBから見たAの速度は\(v-V\)で、衝突後は\(v'-V'\)です。
したがって、運動量保存則を書いてみると、
\begin{equation} m(v'-V'）+M・0=m(v-V)+M・0　\end{equation}
結局
\begin{equation} v'-V'=v-V \end{equation}
となり、(2-4)式とは違った式になってしまいます。

 

 

観測者が（ふたつの物体とは別に）床に対して等速運動している場合は、運動量保存則を利用できます。
計算で確認してみましょう。
観測者が床に対して\(v_0\)の速度で運動している場合を考えます。
衝突前のAとBの、観察者から見た場合の速度は、それぞれ、\(v-v_0\)、\(V-v_0\)、
衝突後は、それぞれ、\(v'-v_0\)、\(V'-v_0\)、です。運動量保存則は、
\begin{equation}
m(v-v_0)+M(V-v_0)=m(v'-v_0)+M(V'-v_0)
\end{equation}
\begin{equation}
mv+MV-mv_0-Mv_0=mv'+MV'-mv_0-Mv_0
\end{equation}
\begin{equation}
mv+MV=mv'+MV'
\end{equation}

 

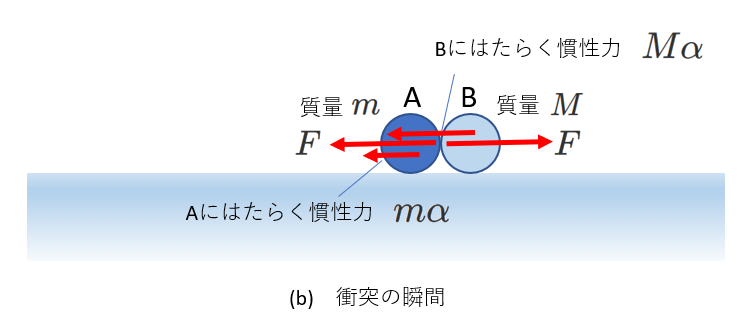
　しかし、観測者が加速している場合は、運動量保存則は使えません。

 

　観測者が加速度\(\alpha\)で加速している場合、ふたつの物体には\(-m\alpha\)、\(-M\alpha\)の慣性力が働きます。ふたつの物体にはたらく慣性力は大きさが異なり、向きは同じです。（右図を参照してください）　これでは、運動量保存則は成り立ちません。

 

　ただし、仮にばねの弾性力などの外力が働いていても、衝突している時間はごく短くて無視できるとし、「衝突の直前と直後の間では運動量保存則が成り立つと考えてよい」としている問題もあります。問題の指示を見逃さないようにしましょう。

 

次に、それぞれの力について考えてみます

 

 

　上の例において、以下に示すように、ふたつの物体の一方が固定されている場合には、運動量保存則は成り立ちません。

 

 

１．ふたつの物体が瞬間的に力を及ぼし合う系

 

ふたつの物体の衝突、合体や分裂などです。
運動量保存則を用いる場合、多くの問題では、

という式を立てます。この式は形式的に書くことができるので、立式ミスを最も少なくできます。
下の 「1-a)衝突してはね返る場合」では、上の形式に則って、\(mv+MV=mv'+MV'\)　という運動量保存の式を立てています。
これを、例えば、\(MV'=(mv+MV)-mv'\)のように書いても式として正しいのですが、ミスが増えるので、
いったんは、\(mv+MV=mv'+MV'\)と書き、それから変形するのが良いでしょう。

 

1-a）衝突してはね返る場合

 

　右のような場合です。ここで、運動量保存則を適用すると、
\begin{equation} mv+MV=mv'+MV' \tag{4-7} \end{equation}
\(v'\)と\(V'\)を求めるためには方程式がもう一つ必要で、それは次のはね返り係数の式（反発係数の式）が使われます。はね返り係数を\(e\)として、
\begin{equation} e=-\frac{V'-v'}{V-v} \tag{4-8} \end{equation}
ふたつの式から、\(v'\)と\(V'\)を求めると、
\begin{equation} V'=\frac{mv(1+e)+V(M-me)}{m+M} \tag{4-9} \end{equation}
\begin{equation} v'=\frac{v(m-eM)+MV(1+e)}{m+M} \tag{4-10} \end{equation}

 

 

　(4-7)式と(4-8)式の方程式を見ると、\(m\)と\(M\)、\(v\)と\(V\)、\(v'\)と\(V'\)をそれぞれ入れ替えても同じ方程式が得られことがわかります。
　そうであれば、方程式を解いた結果もそうなっているはずです。
(4-9)式の右辺について、\(m\)と\(M\)、\(v\)と\(V\)を入れ替えると、(4-10)式の\(v'\)の式が得られます。
このような考え方は検算としても使えます。

 

 

　衝突後に物体Aと物体Bが合体する条件を考えます。このとき、\(v'=V'\)ですから、
\begin{equation} \frac{mv(1+e)+V(M-me)}{m+M}=\frac{v(m-eM)+MV(1+e)}{m+M} \end{equation}
\begin{equation} mv(1+e)+V(M-me)=v(m-eM)+MV(1+e) \end{equation}
\begin{equation} emv-emV=-eMv+eMV \tag{4-11} \end{equation}
\begin{equation} e(m+M)(v-V)=0 \end{equation}
　ここで、\(m+M>0\)、衝突するという条件から、\(V>v\)ですから、\(e=0\)となり、
この場合の衝突が、完全非弾性衝突だということがわかります。

 

注) (4-11)式で両辺を\(e\)で割ってしまわないようにしましょう。
　　数学ならば注意深く計算しても、物理となると深く考えず\(e\)で割ってしまいそうです。
　　\(e\)で割ることは、\(e \not=0\)を考えていることになります。

 

 

　次に、\(m=M\)の場合を考えると、
\begin{equation} V'=\frac{v(1+e)+V(1-e)}{2} \end{equation}
\begin{equation} v'=\frac{v(1-e)+V(1+e)}{2} \end{equation}
　これから、\(v'+V'=v+V\)です。
　さらに完全非弾性衝突（\(e=0\)）という条件を付けると、\(v'=V'=\frac{v+V}{2}\)、
一方、弾性衝突（\(e=1\)）という条件であれば、\(V'=v\)、\(v'=V\)となり、
衝突により、Aの速度とBの速度が入れ替わることがわかります。

 

注）　力学的エネルギー保存とはね返り係数の関係を確認しておきます。
　　はね返り係数が\(e=1\)のときのみ、力学的エネルギーが保存されます。　
　　\(e=1\)が示されていない場合や、弾性衝突と記述されていない場合には、力学的エネルギー保存を用いることはできません。

 

 

 

 

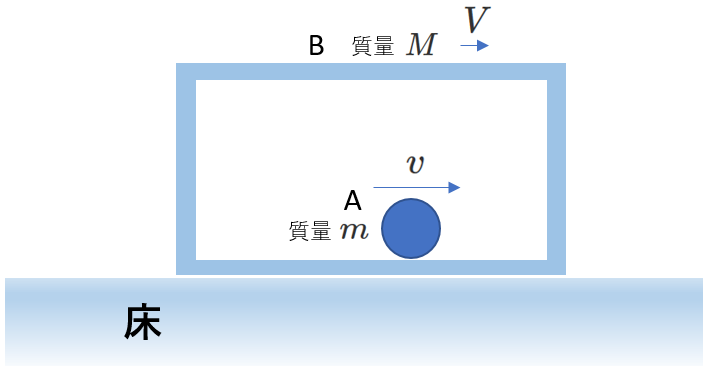
　状況はまるで違っているように見えて、実は普通の衝突と同じという例を右図に示します。

 

　右図で、箱Bの中の物体Aが速度\(v\)で、また、箱B自身も速度\(V(V\gt0)\)で動いています。
床と箱Bの間、および、箱Bと物体Aの間には摩擦がないとします。

 

　AがBに衝突するまで、AとBの間に力のやり取りはありません。
Aは、Bとは無関係に床に対して速度\(v\)でBの上を滑っていきます。
したがって、衝突後のAとBの速度をそれぞれ\(v'\)、\(V'\)として、運動量保存則は（4-7）式とまったく同じに、
\begin{equation} mv+MV=mv'+MV' \end{equation}
となります。

 

 

1-b）物体が一体化する場合

 

　ふたつの物体が合体した問題では、一体化後のふたつの物体の速度が同じであることを運動量保存の式に表します。

 

 

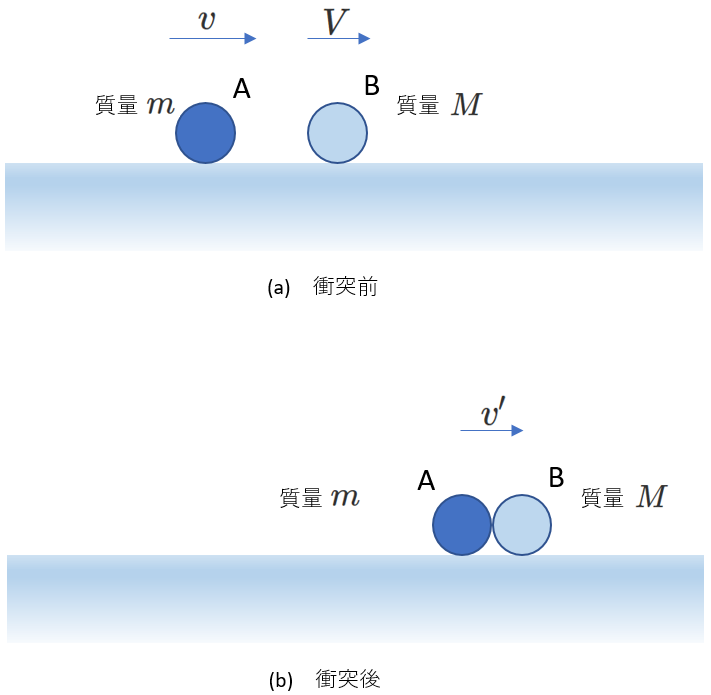
　上の図で、ふたつの物体AとBが衝突したあと一体化したことで、どちらも速度が\(v'\)となっています。
（衝突後、はね返りがなかったということであって、”一体化”という言葉は適していないかもしれないですね。）

 

　「衝突前の物体Aと物体Bの運動量の和」=「衝突後の物体Aと物体Bの運動量の和」という形の運動量保存の式を立てると、
\begin{equation} mv+MV=mv'+Mv'=(m+M)v' \tag{4-14} \end{equation}
これから、\(v'=\frac{mv+MV}{m+M}\) となります。
衝突後のAとBの速度が同じなので、ひとつの方程式で衝突後の速度を求めることができます。

 

　この場合の、はね返り係数\(e\)を求めておきましょう。
\begin{equation} e=-\frac{v'-v'}{V-v}=0 \end{equation}
つまり、これは完全非弾性衝突であることがわかります。逆に、\(e=0\)であれば、「はね返り係数の分子 = 衝突後のふたつの物体の相対速度」が0ということですから、一体化することがわかります。

 

　さて、これはわかりやすい合体の例でした。これとは状況が異なりますが、運動量保存の式が（一体化の場合の）(4-14)式と同じようになる例を以下に紹介します。

 

 

 

1-b-1)　最初の例は、一体化のイメージに近いものです

 

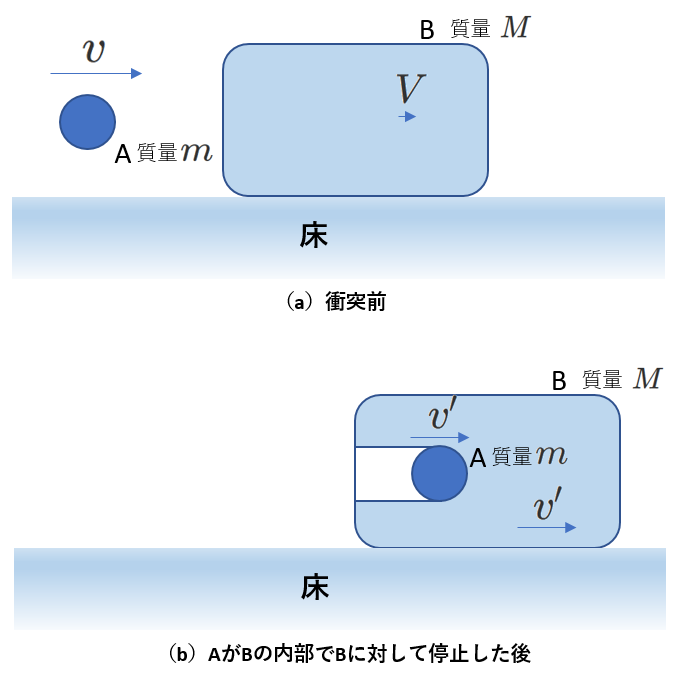
　摩擦のない床上で、速度\(v\)の物体Aが、速度\(V （ｖ \gt Ｖ）\)の物体Bに衝突します。物体AはそのままBに潜り込みますが、Bから抵抗力を受けるため、ある距離進んだところで、Bに対して静止します。
一方、物体BはAから同じ大きさで逆向きの抵抗力を受けます。これによって、物体Bは速度を変化させます。
Aが物体Bに対して静止したときの速度を\(v'\)として、その大きさを求めてみます。
　AとBは同じ速度になっているはずですから、物体Bの速度も\(v'\)です。物体AがB中を進むとき、抵抗力がはたらきますが、その大きさやはたらく時間を吟味することなく、運動量保存則を使えば、\(v'\)を求めることができます。
　「衝突前の運動量の和」=「物体AがBに対して静止した瞬間の運動量の和」という式を立てることにします。
　すると、
\begin{equation} mv+MV=mv'+Mv' \end{equation}
となります。

 

 

1-b-2)　次も、最終的に同じ速度になるという例です

 

 

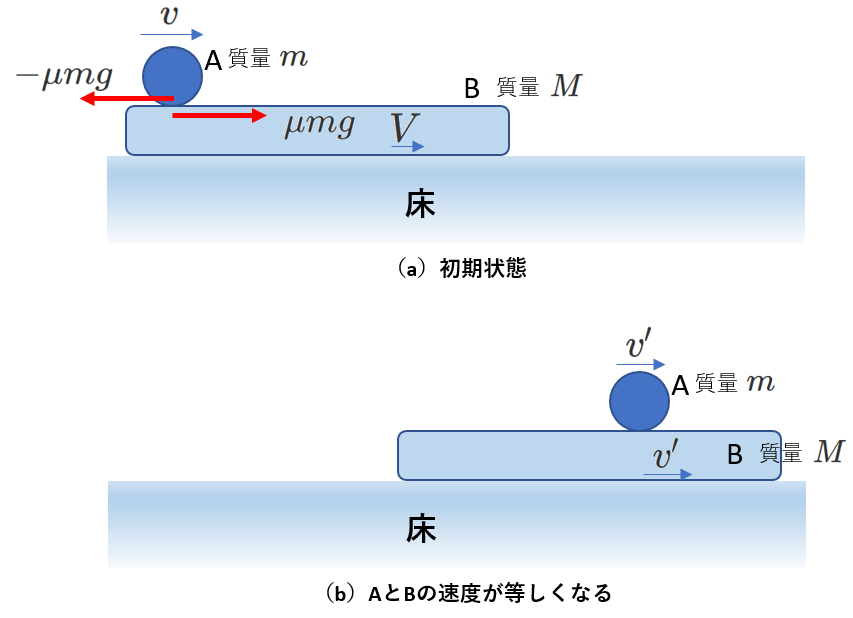
　床と板Bとの間に摩擦はありませんが、板Bと物体Aとの間には摩擦が存在し、その動摩擦係数を\(\mu\)とします。初期状態では、物体Aの速度は\(v\)、板Bの速度は\(V\)で、\(v>V\)の場合を考えます。物体Aは板Bから\(\mu mg\)の大きさの摩擦力を左向きに受け、速度は減少します。同時に、板Bは物体Aから\(\mu mg\)の大きさの摩擦力を右向きに受け、速度は増加します。このようにして、AとBの速度は等しくなります。
　速度が等しくなるということは、物体Aは板Bに対して静止するということで、静止すれば、動摩擦力ははたらかないので、そのままの状態が続くことになります。

 

　この等しくなったときの速度を\(v'\)として、その大きさを求めてみます。　「初期状態の運動量の和」=「物体AとBの速度が等しくなったときの運動量の和」という式を立てます。
\begin{equation} mv+MV=mv'+Mv'=(m+M)v' \end{equation}
となります。

 

　この例題を使って、色々検討してみましょう。ふたつの物体が衝突する場合は衝突の瞬間にのみ相互に力がはたらきますが、板と物体の間にはたらく摩擦は速度が同じになるまで常に一定の力としてはたらきます。　したがって、物体Aも板Bも等加速度運動となります。

 

　最初に、物体Aの速度が\(v\)から\(v'\)になるまでの時間 \(t\)を求めてみましょう。力積と運動量の変化量の関係を用います。物体AがBから受ける力積は（負号に注意して）\(-\mu mg\cdot t\) です。これにより、Aの運動量が\(mv\) から\(mv'\) に変化します。式に表せば、
\begin{equation} mv'-mv=-\mu mgt \tag{4-15} \end{equation}
\(v'\)がわかっているので、上式から \(t\) がわかります。

 

 

 

 

 

 

 

 

1-c）一つの物体が分裂する場合

 

　物体が破裂する場合や、宇宙船が探査機を打ち出すなどの問題例があります。

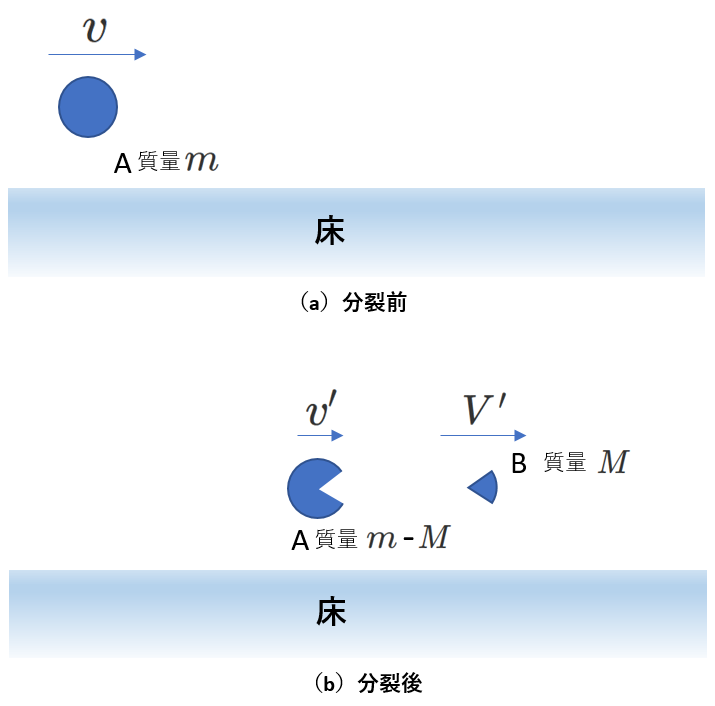
　右図は、質量\(m\)、速度\(v\)の物体Aが、質量\(M\)の物体Bを打ち出す場合です。打ち出した後の、物体AとBの床に対する速度をそれぞれ\(v'\)、\(V'\)とすれば、運動量保存の式は、
\begin{equation} mv=(m-M)v'+MV' \end{equation}
となります。分裂後の物体Aの質量が\(m-M\)であることに注意しましょう。
　この場合、未知数は\(v'\)と\(V'\)のふたつです。したがって、\(v'\)と\(V'\)を求めるにはもうひとつの条件（あるいは、方程式）が必要になります。
\(v'\)と\(V'\)のどちらかが既知であるとする問題もあります。

 

　物体Aが静止している場合\((v=0)\)には、上の式は、
\begin{equation} (m-M)v'=-MV' \end{equation}
と変形でき、\(m-M>0\)であることから、物体AとBは逆向きに進むことがわかります。

 

　繰り返しになりますが、運動量保存は成立しても、力学的エネルギー保存が成立しない場合が多くあります。
この場合も力学的エネルギー保存が成立しません。
物体Aを分裂する(物体Bを打ち出す）のにエネルギーを使っているはずで、その分だけ力学的エネルギーが増えているはずです。　

 

 

 

1-d）一方の物体が他方を貫通する場合

 

　右図のような場合です。
　運動方程式は、
\begin{equation} mv+MV=mv'+MV' \end{equation}
となります。
　この場合も、未知数は\(v'\)と\(V'\)のふたつです。したがって、\(v'\)と\(V'\)を求めるにはもうひとつの条件（あるいは、方程式）が必要になります。
\(v'\)と\(V'\)のどちらかが既知であるとする問題もあります。

 

 

　右に3つの例を示しました。
Bは床の上に置かれた車や台で、床との摩擦はなく、
水平方向に自由に動けます。
Bは鉛直方向に動くことはありません。

 

　Bの上に物体Aがあって、
AとBは力を及ぼし合っています。
図（2-a）は、張力
図（2-b）と図（2-c）は、抗力、です。

 

　これらの力は、作用・反作用の法則に従います。

 

　力がこれだけであれば、運動量保存が成立しますが、
Aには重力が働いています。
重力は、地球との間に働く力でAとBからなる系にとっては外力です。
したがって、重力の方向（鉛直方向）には運動量保存は成り立ちません。

 

　しかし、水平方向を考えると、
図（2-a）では、張力の水平方向成分
図（2-b）と図（2-c）では、垂直抗力の水平方向成分
は、AとBの両方にはたらいていて、大きさは等しく、逆向きです。

 

 

　これらのことから、3つの例は、いずれも
運動量の鉛直方向成分は保存されないが、
運動量の水平方向線分は保存されることがわかります。

 

　また、3つの例は、いずれも
系全体（AとB）の力学的エネルギーが保存されます。

 

　AまたはB単独では、保存力ではない張力や抗力がはたらくため、
力学的エネルギーは保存されません。
　しかし、張力や抗力がAにする仕事とBにする仕事は、大きさが等しく、符号が逆であるため、
AとBからなる系を考えた場合、張力や抗力のする仕事は相殺され、
力学的エネルギーの和は保存されます。

 

 

 

　以下に、3つの例についてもう少し詳し説明します。

 

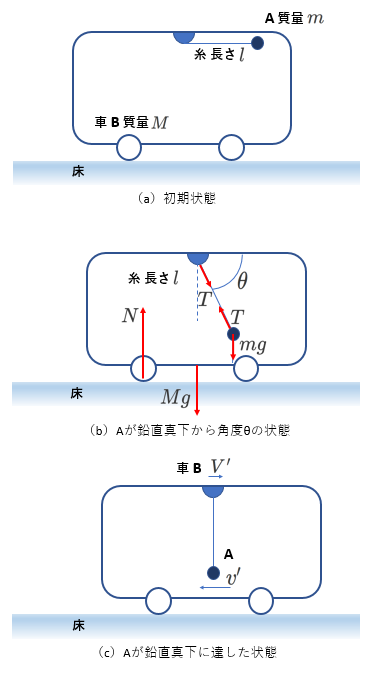
（1） 車の中の振り子

 

 

　床の上に車Bがあり、Bの屋根には質量\(m\)のおもりAが、長さ\(l\)の糸により吊るされています。
Bと床の間に摩擦はないとします。
今、Bが静止した状態で、糸が水平になるようにAを持ち上げ、糸がぴんと張られるようにし、その後Aを離します。（図（a)の状態）

 

　糸が水平方向と角度\(\theta\)になったとき、AとBにはたらく力を図（b）に示しました。
BとAは糸から張力\(T\)を受けます。
Bは鉛直方向には動けませんが、\(T\)の水平成分により、図で右向きに加速されます。

 

　Aの運動は、車の中から見れば、鉛直面内での円運動ですが、
車は加速しているので、車の外から見た場合は、円運動にはなりません。

 

【運動量保存】
　Aには外力である重力がはたらいており、これにより、Aは鉛直方向に加速されます。
したがって、鉛直方向では、運動量は保存されません。
一方、水平方向には糸の張力\(T\)の水平方向成分がAとBに(大きさが同じで、向きが逆に）はたらいていて、
これは内力ですから、水平方向には運動量保存則が成り立ちます。

 

　今、(c)の状態、つまり、糸が鉛直方向に一致したときを考えて、
運動量保存の式を立てると、
\begin{equation} m\times 0+M\times 0=mv'+MV' \tag{5-1} \end{equation}

 

ここで、右図を見て、
\begin{equation} m\times 0+M\times 0=-mv'+MV' \tag{5-1'} \end{equation}
と立式する場合もありますが、
この場合、\(V'\)は右向きが正の向き、\(v'\)は左向きが正の向きと考えていることになります。

 

 

【力学的エネルギー保存】
　AまたはB単体では、保存力ではない張力が働いているので、力学的エネルギーの保存則は成立しませんが、
AとBからなる系の力学的エネルギーの和を考えると保存されます。
位置エネルギーの基準を（ｃ）の状態の位置として、
\begin{equation} \frac{1}{2}m\times 0^2+\frac{1}{2}M\times 0^2+mgl=\frac{1}{2}mv'^2+\frac{1}{2}MV'^2+mg\times0 \tag{5-2} \end{equation}

 

　（5-1）式と（5-2）式から、\(v'とV'\)を求めることができます。

 

 

 

 

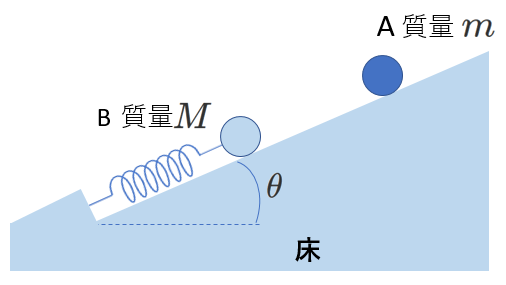
（2）　自由に動く斜面体の上で滑る物体

 

　次の例は、床の上に斜面台Bがあり、その上を質量\(m\)の物体Aが斜面を滑る場合を考えます。
床と斜面台の間には摩擦はないとします。　
右の図では、摩擦がないことを、斜面台に取り付けた車輪で表しています。

 

 

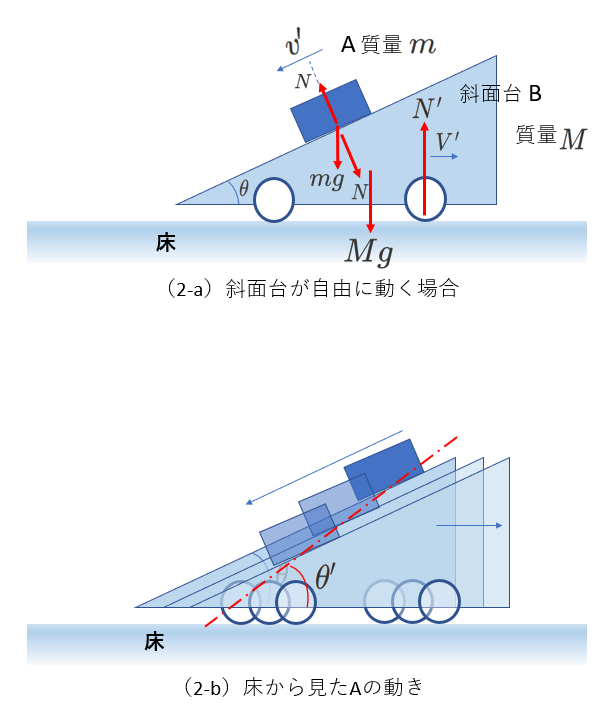
　初期状態では、AもBも静止していて、
時刻\(t=0\)でAを離し、
\(t\) 秒後にAが斜面上を\(l\)の距離進んだ時の速さが\(v'\)、
Bの速さが\(V'\)になったものとします。
このときAとBにはたらく力を右図に表しました。

 

　BとAは抗力\(N\)を及ぼし合っています。
Bは鉛直方向には動けませんが、\(N\)の水平成分により、図で右向きに加速されます。

 

　Aの運動は、斜面台の上から見れば、
水平面との角度\(\theta\)で滑り降りる等加速度運動ですが、
斜面台も加速しているので、
床から見た運動の水平面との角度は、\(\theta\)にはなりません。

 

【運動量保存】
　Aには外力である重力がはたらいており、
これにより、Aは鉛直方向に加速されます。
したがって、鉛直方向では、運動量は保存されません。

 

　一方、水平方向には垂直抗力\(N\)の水平方向成分が
AとBに（大きさが同じで、向きが逆に）はたらいていて、
これは内力ですから、水平方向には運動量保存則が成り立ちます。

 

　運動量保存の式を立てる上で注意するのは、
「（1） 車の中の振り子」の場合と異なって、
Aの速度\(v'\)の向きは水平方向から角度\(\theta'(\neq\theta)\)傾いていることです。
つまり、角度\(\theta'\)が不明であるため、\(theta'\)を使って、\(v'\)の水平方向成分を表すことができません。

 

　そこで、Aの速度\(v'\)の水平方向成分を\(v_x'\)、鉛直方向成分を\(v_y'\)として、
　水平方向の運動量保存の式は、
\begin{equation} m\times 0+M\times 0=mv_x'+MV' \tag{5-3} \end{equation}
となります。
　ここで、水平方向の速度の正の向きを左向き、鉛直方向の速度の正の向きを上向きとしています。

 

【力学的エネルギー保存】
　AまたはB単体では、保存力ではない垂直抗力が働いているので、力学的エネルギーの保存則は成立しませんが、
AとBからなる系の力学的エネルギーの和を考えたときには、保存されます。
位置エネルギーの基準を\(t=0\)のときのAの位置として、
\begin{equation} \frac{1}{2}m\times 0^2+\frac{1}{2}M\times 0^2+mg\times 0=\frac{1}{2}m(v_x'^2+v_y'^2)+\frac{1}{2}MV'^2-mgl\sin\theta \tag{5-4} \end{equation}
Aの運動エネルギーは、\(\frac{1}{2}m(v_x'^2+v_y'^2)\)であって、\(\frac{1}{2}mv_x'^2\)ではないことに注意しましょう。

 

【付随的条件】
　（5-3）（5-4）式では未知数が、\(v_x'、v_y'、V'\)の3個ですから、方程式が1個足りません。
もうひとつは、斜面体の上から見たとき、物体Aは水平面に対して角度\(\theta\)で直線運動する、ことを使います。
　すなわち、斜面体から見た物体Aの速度の鉛直方向成分は\(v_y'\)、
　水平方向成分は、\(v_x'-V'\)ですから、
\begin{equation} \tan\theta=\frac{|v_y'|}{|v_x'-V'|}=\frac{-v_y'}{v_x'-V'} \tag{5-5} \end{equation}
です。
　「水平方向の速度の正の向きを左向き、鉛直方向の速度の正の向きを上向き」から、\(v_y'<0\)、\(v_x'-V'>0\)です。

 

　これで方程式が3式揃いました。
(5-3)(5-4)(5-5)式を連立させて解けば、\(v'_x、v'_y、V'\)を求めることができます。

 

　尚、（5-5）式を採用する場合、\(v'_y\)の正の向きは、鉛直上向きです。
したがって、解けば、\(v'_y \lt 0\)の答えが得られます。

 

　一方、
\begin{equation} \tan\theta=\frac{v_y'}{v_x'-V'} \tag{5-5'} \end{equation}
という式を立てれば、\(v'_y\)の正の向きは、鉛直下向きで、\(v'_y \gt 0\)の答えが得られます。
ここで、（5-3）式も(5-4)式も、v'_yの正負には無関係に立式されています。

 

 

注）この例では、
　　物体Aが斜面を滑りおりる設定でしたが、
　　逆に、物体が初速度を与えられて、斜面を登る設定もあります。

 

　　　この場合、Aの速度の水平方向成分の向きとBの速度の向きは同じになります。
　　そして、Aの速さは登るにつれて遅くなり、
　　鉛直方向の速さが\(0\)となる瞬間があります。
　　この瞬間はAとBの水平方向の速さが等しくなります。

 

　　　このことから、この瞬間の速さを、運動量保存の式だけから求めることができます。
　　Aの速度の鉛直方向成分は\(0\)なので、（5-5）式を考える必要はありません。

 

 

 

 

（3）　円筒内面を滑る物体

　

　床の上に円筒内面を持つ車Bがあります。　
　右図に円筒内面の断面が示されていますが、ちょうど半円で、
その端に質量\(m\)の物体AがBの内面に接触した状態で固定されています。（図(a)の状態）
円筒内面の断面の円の半径は\(r\)です。

 

　Aを離したあとのAの運動を考えますが、
Aは、図の断面に沿って運動するものとします。
また、AとBの内面の間に摩擦はありません。

 

　Aと半円の中心を結ぶ線が鉛直方向となす角度が\(\theta\)になったときにAとBにはたらく力を図(b)に示しました。
角度の定義が「(1) 車の中の振り子」と異なります。
　BとAは垂直抗力\(N\)を及ぼし合います。
Bは鉛直方向には動けませんが、\(N\)の水平方向成分により、図で左向きに加速されます。

 

　Aの運動は、Bから見れば、鉛直面での円運動ですが、
Bが加速しているので、床上から見た場合は、円運動にはなりません。

 

【運動量保存】
　Aには外力である重力がはたらいており、これにより、Aは鉛直方向にも加速されます。
したがって、鉛直方向では、運動量は保存されません。
一方、水平方向には垂直抗力\(N\)の水平方向成分がAとBに(大きさが同じで、向きが逆に）はたらいていて、
これは内力ですから、水平方向には運動量保存則が成り立ちます。

 

　今、図(c)の状態、つまり、Aが円運動の円の中心の鉛直真下に達した瞬間を考えて、
運動量保存の式を立てると、
\begin{equation} m\times 0+M\times 0=mv'+MV' \tag{5-6} \end{equation}

 

【力学的エネルギー保存】
　AまたはB単体では、保存力ではない垂直抗力が働いているので、力学的エネルギーの保存則は成立しませんが、
AとBからなる系の力学的エネルギーの和を考えると保存されます。
位置エネルギーの基準を図(c)の状態の位置として、
\begin{equation} \frac{1}{2}m\times 0^2+\frac{1}{2}M\times 0^2+mgr=\frac{1}{2}mv'^2+\frac{1}{2}MV'^2+mg\times0 \tag{5-7} \end{equation}

 

　（5-6)式と（5-7）式から、\(v'とV'\)を求めることができます。

 

　これまで、外力がはたらいているときには運動量（または、その和）は保存されない、
と説明してきました。
　しかし、問題によっては、外力がはたらいている状態、
あるいは、はたらき得る状態でも運動量が保存されるとして問題を解く場合があります。

 

　それは、次のいずれかの場合で、多くの場合、問題に注釈があります。
問題文をしっかり読むことが大事です。

 

a)　ふたつの物体の衝突などで、衝突の瞬間にはたらく力が外力に比べてはるかに大きい場合
b)　ふたつの物体の衝突などで、力を及ぼし合う時間が非常に短いため、
　　対象が動かず、ばねの弾性力などの影響が小さいとみなせる場合

 

（1）片一方の物体がばねにつながれている場合

 

　右図は、ばねにつながれたおもりB（質量\(M\)）に物体A（質量\(m\)）が衝突する例です。
ばねは自然長の状態で、Ｂは静止しています。

 

　衝突したとき、ＡとBは\(F\Delta t\)の力積を及ぼし合います。

 

　\(\Delta t\)は\(0\)ではなく、有限な時間ですから、
この間に、わずかですがばねが伸び縮みするでしょう。

 

　そうすると、Bのみにばねの弾性力が\(v\)の方向（衝突の方向）にはたらき、
この力はAとBからなる系に対して外力ですから、
運動量は保存されないということになります。

 

　しかしながら、衝突の時間\(\Delta t\)は短く、
このため、衝突時にAとBが及ぼし合う力はばねの弾性力よりもはるかに大きいとして、
弾性力の影響を近似的に\(0\)と考えことができる場合があります。

 

　問題文の中に「弾性力を無視してもよい」などの断り書きがある場合があります。
大きなヒントになりますから、問題をじっくり読むようにしましょう。

 

　さて、衝突直前のＡの速度を\(v\)とし、衝突直後のAとBの速度をそれぞれ\(v'、V'\)とすれば、
運動量保存の式は、
\begin{equation} mv+M\times 0=mv'+MV' \end{equation}
となります。

 

　\(v'とV'\)をもとめるためには、もう一つの方程式が必要になります。

 

　これも問題に与えられているはずです。
例えば、「衝突後は、AとBは一体となって運動する」や、
「反発係数」が、与えられます。

 

　衝突後のBの運動は、（物体AがBの運動を邪魔しないとして）
つり合いの位置（振動の中心）で初速度を与えられたおもりの単振動ということになります。

 

 

 

　例をもうひとつ、
　右図のように、
坂道に設置されたばねのおもりBに物体Aが衝突する場合も
近似的に成り立つとしてよい場合があります。
この場合には、弾性力以外に、AにもBにも外力である重力が
衝突の\(\Delta t\)の間働いているため、厳密には保存則は成り立ちません。

 

　さて、「Bは最初は静止していて、
Aと斜面、Bと斜面の間に摩擦はないとします。
この状態では、ばねは縮んだ状態にあり、
Bにはたらく重力の斜面方向成分とばねの弾性力がつりあっています。

 

 

　衝突直前のＡの速度を\(v\)とし、衝突直後のAとBの速度をそれぞれ\(v'、V'\)とすれば、
運動量保存の式は、
\begin{equation} mv+M\times 0=mv'+MV' \end{equation}
となります。

 

　\(v'とV'\)をもとめるためには、もう一つの方程式が必要になります。

 

　これも問題に与えられているはずです。
例えば、「衝突後は、AとBは一体となって運動する」や、
「反発係数」が、与えられます。

 

　衝突後のBの運動は、（物体AがBの運動を邪魔しないとして）
つりあいの位置（振動の中心）で初速度を与えられたばねにつながれたおもりの単振動ということになります。
ただし、衝突後にAとBが一体化した場合、
つりあいの位置（振動中心）は衝突前のBの位置からずれることに注意しましょう。

 

　また、衝突直前のAの速度が与えられていなくて、
AがBから高さ\(h\)にあるときの速度で与えられているような場合は、
Aの衝突直前の速度を求める必要があります。

 

 

 

　　

 

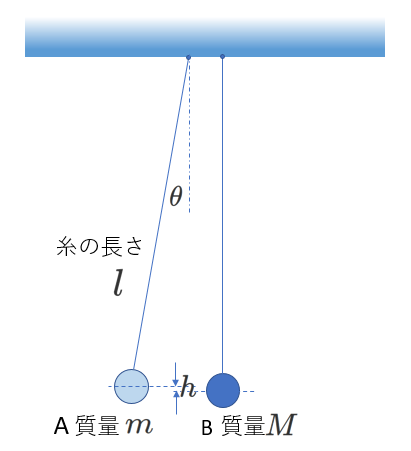
（2） 糸で吊るされたふたつのおもりの衝突

 

　鉛直につりさげた状態でちょうどふたつのおもりが接するように配置されています。
その片一方Aを、糸がぴんと張った状態で、角度\(\theta\)まで持ち上げ、しずかに離します。
Aの糸が鉛直になった瞬間に静止していたBと衝突します。

 

　衝突直前のAの速度を\(v\)、
衝突直後のAとBの速度をそれぞれ\(v'、V'\)とすると、

 

　運動量保存の式は、
\begin{eqnarray} mv+M\times 0&=&mv'+MV' \\
mv&=&mv'+MV' 　\tag{6-1}
\end{eqnarray}
となります。

 

 

 

 

（3） 重力がはたらいている場合

 

　下図の状況を考察します。
物体AとBが床から高さ\(h\)のところに固定されています。
Aだけ、そのまま落下させ、床に衝突した瞬間を時刻\(t=0\)、
床とAの衝突は弾性衝突、AとBの衝突のはね返り係数を\(e\)とします。

 

Aははね返ったのち、\(t=0\)で放されたBと衝突します。
衝突後のAとBの速さを求めることにします。

 

 

　この問題は、運動の順序にしたがって、考えれば答えが得られます。
2回の衝突があります。

 

　1回目は物体Aと床の衝突です。
床は固定されている(床が動かないように外から力がはたらいている）ので、
物体Aと床からなる系の運動量は保存されません。
　しかし、はね返り係数の式は成り立つので、
弾性衝突という条件から、考察ができます。
運動量保存が成立しなくても、はね返り係数の式は成立します。

 

　2回目の衝突は、AとBの衝突です。
この衝突の間、AとBには重力がはたらいています。
重力はAとBに対して同じ方向にはたらいていて、明らかに外力です。

 

　しかし、近似的に運動量保存則が成り立つとして解きます。
問題文中に、近似的に運動量保存則が成り立つとしてよいという文章がある場合があります。
例えば、次のような文章です。
　衝突は瞬間的であるので、
　　衝突の間のAとBにはたらく重力の影響（力積）を無視することができる。

 

 

　さて、解法の手順は、
（1）Aの床に衝突する直前の速度\(v_o\)を求めます。力学的エネルギー保存則を使います。

 

（2）床に衝突した直後のAの速度\(v'_o\)を求めます。はね返り係数の式と弾性衝突という条件を使います。

 

（3）AとBが衝突する時刻\(t_1\)を求めます。
　　　\(t>0\)では、AにもBにも重力がはたらいています。
　　　AとBの加速度はともに\(-g\)です。
　　「衝突する」という条件は、等価な別の条件を設定します。
　　例えば、時刻が同じとか、座標が同じなどです。
　　ここでは、直接的な「座標が同じ」を使うのがよさそうです。

 

　　また、AとBは\(-g\)の等加速度運動、つまり、放物運動なので、
　　座標も簡単に求めることができそうです。

 

（4）衝突直前のAとBの速度\(v'、V'\)を求めます。

 

 

（5）衝突直後のAとBの速度\(v、V\)を求めます。
　　はね返り係数の式と、
　　近似的に、運動量保存則を使います。

 

 

　では、実際に求めてみましょう。

 

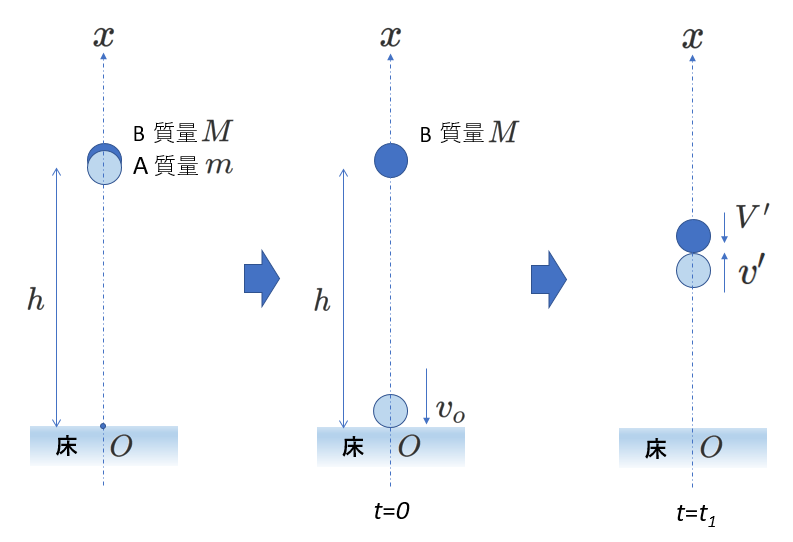
（1） 床に衝突する直前のAの速度\(v_o\)
　重力の位置エネルギーの基準を原点\(O\)にとり、
　「\(x=h\)でのAの力学的エネルギーの大きさ」=「衝突直前のAの力学的エネルギーの大きさ」
　という式を立てます。
　\begin{eqnarray} \frac{1}{2}m\times 0+mgh&=&\frac{1}{2}mv_o^2+mg\times 0 \\
mgh&=&\frac{1}{2}mv_o^2 \\
これより&& \\
　v_o&=&-\sqrt{2gh}
\end{eqnarray}
注）　\(+x\)向きを\(v_o\)の正の向きとしています。

 

（2）床に衝突した直後のAの速度\(v'_o\)

　はね返り係数の式を立てると、
\begin{eqnarray} 1&=&-\frac{v'_0-0}{v_0-0} \\
1&=&-\frac{v'_0}{v_0} \\
v'_o&=&-v_o　　\\
　\\
すなわち、&&v'_o は上向きで大きさがv_o　に等しい。
\end{eqnarray}

 

（3） AとBが衝突する時刻\(t_1\)
　AとBの加速度は\(-g\)です。
　これから、時刻\(t\)のAとBの\(x\)座標\(x_A、x_B\)は次のように表されます。
　\begin{eqnarray} 　x_A&=&0+v'_ot+\frac{1}{2}(-g)t^2 \\
x_B&=&h+0\times t+\frac{1}{2}(-g)t^2 \\
衝突するということは、x_A&=&x_B、であるから、
　v'_ot_1-\frac{1}{2}gt_1^2&=&&h-\frac{1}{2}gt_1^2 \\
これより、t_1&=&\frac{h}{v'_o}=\frac{h}{\sqrt{2gh}}=\sqrt{\frac{h}{2g}}
\end{eqnarray}

 

上の式で両辺の\(-\frac{1}{2}gt_1^2\)が相殺されて、結局\(t_1=\frac{h}{v'_o}\)となっていることに
どのような意味があるのでしょう。

 

　仮に、Aが床ではね返ったときの初速が\(0\)であれば、
A、Bとも自然落下(加速度\(-g\)）で、AとＢの間隔はいつも\(h\)です。
したがって、この距離を\(v'_o\)で進む時間が\(t_1\)ということになります。

 

 

（4）時刻\(t_1\)のAとBの速度\(v'、V'\)
　\begin{eqnarray} v'&=&v'_o-gt_1=\sqrt{2gh}-g\sqrt{\frac{h}{2g}}=\frac{\sqrt{2gh}}{2} \\
V'&=&-gt_1=-\frac{\sqrt{2gh}}{2} \end{eqnarray}

 

（5） 衝突直後のAとBの速度\(v、V\)
　運動量保存の式は、
\begin{eqnarray} mv'+MV'&=&mv+MV \\
\frac{\sqrt{2gh}}{2}(m-M)&=&mv+MV \tag{6-8}
\end{eqnarray}

 

はね返り係数の式は、
\begin{eqnarray} e&=&-\frac{v-V}{v'-V'} \\
&=&-\frac{v-V}{\sqrt{2gh}} \tag{6-9}
\end{eqnarray}

 

(6-8)(6-9)式から、\(v、V\)が得られます。
\begin{eqnarray} v&=&\frac{m-(1+2e)M}{2(M+m)}\sqrt{2gh} \\
V&=&\frac{m(1+2e)-M}{2(M+m)}\sqrt{2gh}
\end{eqnarray}

 

１．外力が働く場合

 

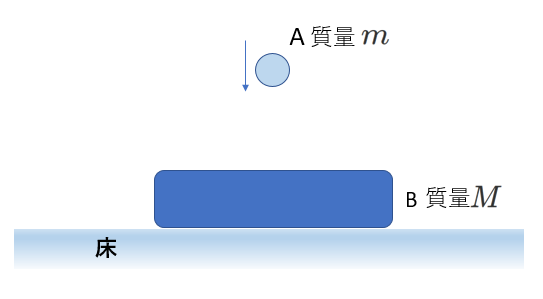
1-a）テーブルの上の物体に上から別の物体が衝突する場合

 

　右図のような状況で、Bは外力である床からの垂直抗力を受けるので、運動量保存則は成り立ちません。
ただし、この場合にも、はね返り係数の式は成り立ちます。

 

 

 

 

２．観測する条件によるもの

 

2-a）　観測者が観測対象の物体上にいる場合

 

2-b）　観測者が加速している場合

 

　この場合、ふたつの物体に外力である慣性力が働くので、慣性系から観察したときのような運動量保存則は成り立ちません。

　水平面上で２つの物体が衝突し、別々の角度に進むときは、運動量保存則を2次元で考えます。
このとき、運動量保存の式はベクトルを用いた式で表されます。

 

　具体的な例で考えてみます。

 

 

 

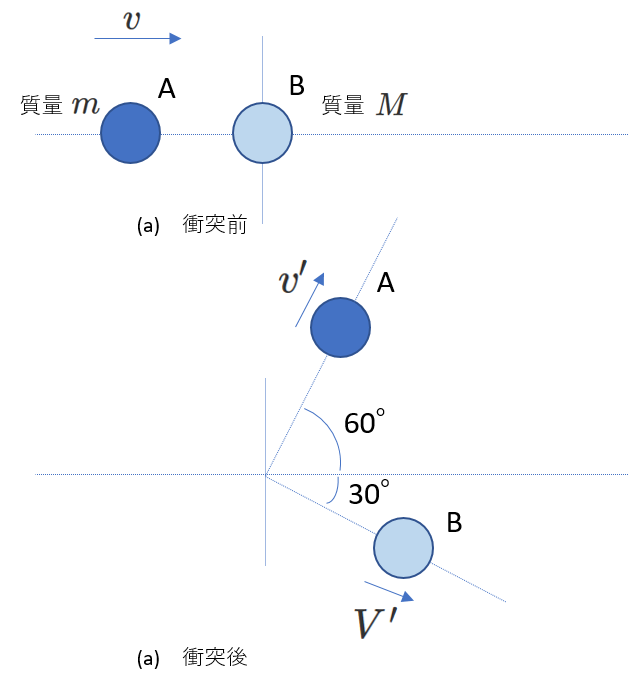
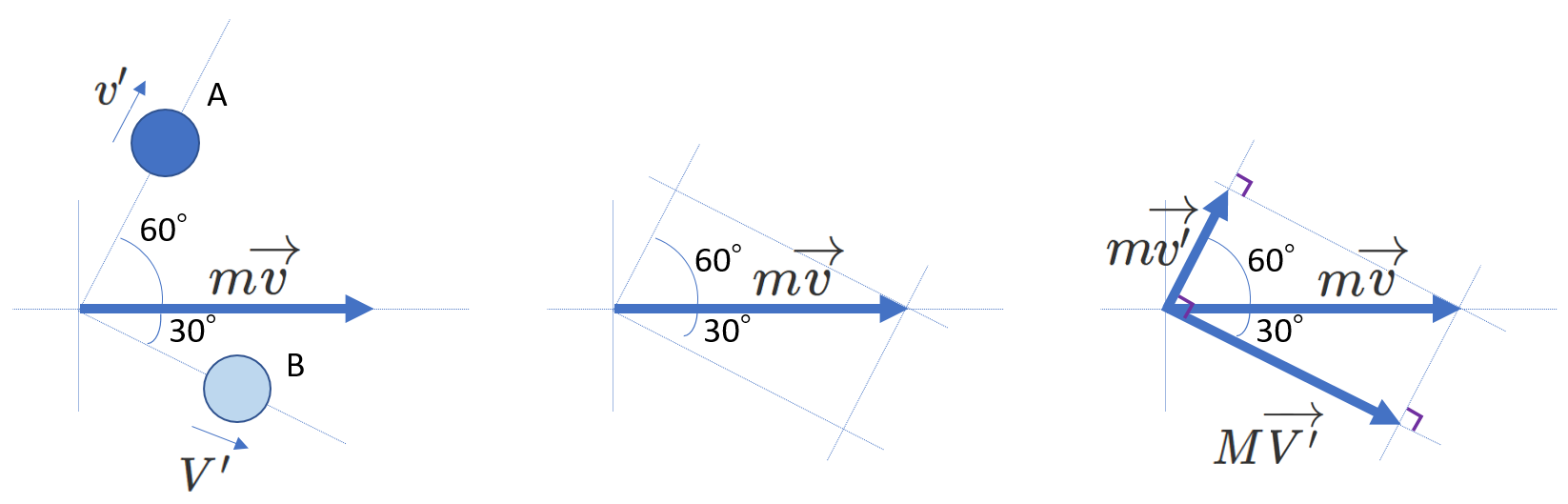
　右図は、水平面上のふたつの物体の衝突を鉛直上方から見た図です。静止している物体B（質量\(M\)）に速さ\(v\)の物体A（質量\(m\)）が衝突します。衝突後、物体Aは衝突前の進行方向に対して60°の方向に、物体Bは30°の方向に進みました。衝突後のAとBの速さを求めてみましょう。

 

衝突前のAの速度を\(\overrightarrow{v}\)、衝突後のAの速度を\(\overrightarrow{v'}\)、Bの速度を\(\overrightarrow{V'}\) とします。
すると、運動量保存の式は、
\begin{equation} m\overrightarrow{v}=m\overrightarrow{v'}+M\overrightarrow{V'} \tag{8-1} \end{equation}
となります。

 

　この式から、衝突後のAとBの速さ（すなわち、\(\overrightarrow{v'}\)と\(\overrightarrow{V'}\)の大きさ）を求めるには、ベクトル図を使う方法とベクトルの成分を使う方法があります。

 

 

 

a)　ベクトル図を使って解く

 

　下図にベクトル図の描き方を示しました。
図を描くのに用いる条件は、60°と30°の角度と、(8-1)式です。
衝突前の運動量の総和は、\(m\overrightarrow{v}\)で右向きです。さらに、60°と30°の角度を描き入れます。
次に、Aの進行方向に平行で、\(m\overrightarrow{v}\)の矢印の先端を通る直線と、Bの進行方向に平行で、\(m\overrightarrow{v}\)の矢印の先端を通る直線を引きます。（中央図）　こうして、衝突後の運動量、\(m\overrightarrow{v'}\)と\(M\overrightarrow{V'}\)が決定されます。このとき、直角記号をつけたところが直角であることが幾何的にわかります。（右図）

 

　下図から、次の関係式が求められます。
\begin{equation} \cos(\frac{\pi}{3})=\frac{m|\overrightarrow{v'}|}{m|\overrightarrow{v}|} \end{equation}
\begin{equation} \cos(\frac{\pi}{6})=\frac{M|\overrightarrow{V'}|}{ｍ|\overrightarrow{v}|} \end{equation}

 

これより、
\begin{equation} |\overrightarrow{v'}|=\frac{|\overrightarrow{v}|}{2}、|\overrightarrow{V'}|=\frac{\sqrt{3}m}{2M}|\overrightarrow{v}| \end{equation}
が、得られます。

 

 

 

 

b)　ベクトルの成分を使って解く

 

 

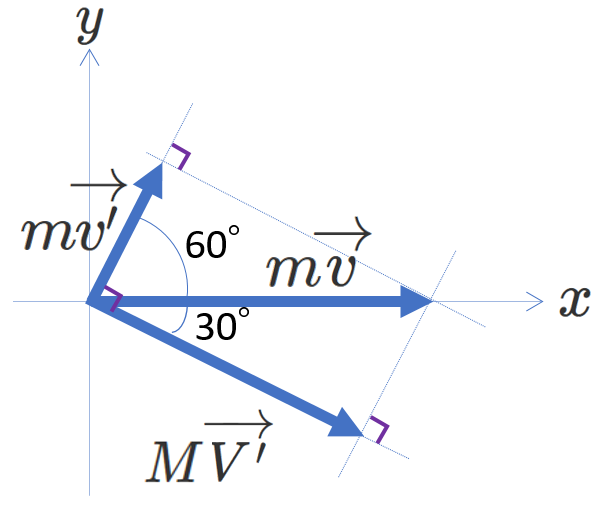
　ｘ軸とｙ軸を、右の図のように決めます。すると、各ベクトルの成分は次のように書くことができます。

 

\begin{equation} m\overrightarrow{v}=(m|\overrightarrow{v}|,0) \end{equation}
\begin{equation} m\overrightarrow{v'}=(m|\overrightarrow{v'}|\cos\frac{\pi}{3},m|\overrightarrow{v'}|\sin\frac{\pi}{3}) \end{equation}
\begin{equation} m\overrightarrow{V'}=(m|\overrightarrow{V'}|\cos\frac{\pi}{6},-m|\overrightarrow{V'}|\sin\frac{\pi}{6}) \end{equation}

 

　これらを用いて(10）式を書き改めると、
\begin{equation} (m|\overrightarrow{v}|,0)= (m|\overrightarrow{v'}|\cos\frac{\pi}{3},m|\overrightarrow{v'}|\sin\frac{\pi}{3})+(m|\overrightarrow{V'}|\cos\frac{\pi}{6},-m|\overrightarrow{V'}|\sin\frac{\pi}{6}) \end{equation}
成分ごとにわけると、
\begin{equation} m|\overrightarrow{v}|= m|\overrightarrow{v'}|\cos\frac{\pi}{3}+M|\overrightarrow{V'}|\cos\frac{\pi}{6} \end{equation}
\begin{equation} 0=m|\overrightarrow{v'}|\sin\frac{\pi}{3}-M|\overrightarrow{V'}|\sin\frac{\pi}{6} \end{equation}

 

　これを解くと、
\begin{equation} |\overrightarrow{v'}|=\frac{|\overrightarrow{v}|}{2}、|\overrightarrow{V'}|=\frac{\sqrt{3}m}{2M}|\overrightarrow{v}| \end{equation}
「a)　ベクトル図を使って解く」と同じ結果になりました。

 

　ふたつの解き方を比較してみると、
「b)　ベクトルの成分を使って解く」では、式を形式的に立てることができるので、ミスが少なくなります。しかし、立式した後の式の変形がめんどうです。
　一方、「a)　ベクトル図を使って解く」では、ベクトル図を描くのに慣れる必要がありますが、いったん図が描ければ、（問題は解きやすい角度になっていることもあって）、計算は直観的にできます。自分が解きやすいと思う方法を使えばよいですが、「ベクトル図を描け」という問題も出題されることがあるので、どちらでも解けるようにしておきましょう。

 

　衝突がはね返り係数（反発係数）\(e=1\)の弾性衝突のとき、力学的エネルギーが保存されることを証明します。

 

 

　運動量保存則は、
\begin{equation} mv+MV=mv'+MV' \tag{9-1} \end{equation}
　はね返り係数の式は、
\begin{equation} e=-\frac{v'-V'}{v-V}=1 \tag{9-2} \end{equation}

 

　力学的エネルギー保存則は、
\begin{equation} \frac{1}{2}mv^2+\frac{1}{2}MV^2=\frac{1}{2}mv'^2+\frac{1}{2}MV'^2 \tag{9-3} \end{equation}

 

（9-1）式と（9-2）式から（9-3)式を導きます。具体的には、（9-1）式と（9-2）式から\(v\)と\(V\)を式で表し、これらを（9-3）式の左辺に代入し、（9-3）式の右辺が導かれることを確認します。

 

（9-2）式から、　
\begin{equation} v-V=-v'+V' \tag{9-4} \end{equation}

 

\begin{eqnarray} (9-1)+M\times(9-4) \qquad mv+MV&=&mv'+MV' \tag{9-1} \\
Mv-MV&=&-Mv'+MV' \tag{M×(9-4)} \\
(m+M)v&=&(m-M)v'+2MV'
\end{eqnarray}
したがって、
\begin{equation} v=\frac{m-M}{m+M}v'+\frac{2M}{m+M}V'　\tag{9-5} \end{equation}

 

\begin{eqnarray} (9-1)-m\times(9-4) \qquad mv+MV&=&mv'+MV' \tag{9-1} \\
mv-mV&=&-mv'+mV' \tag{m×(9-4)} \\
(m+M)V&=&2mv'+(M-m)V'
\end{eqnarray}
したがって、
\begin{equation} V=\frac{2m}{m+M}v'-\frac{m-M}{m+M}V'　\tag{9-6} \end{equation}

 

(9-5)式と（9-6）式を（9-3）式の左辺に代入します。
\begin{eqnarray}
\frac{1}{2}mv^2+\frac{1}{2}MV^2&=& \frac{1}{2}m\left(\frac{m-M}{m+M}v'+\frac{2M}{m+M}V'\right)^2+\frac{1}{2}M\left(\frac{2m}{m+M}v'-\frac{m-M}{m+M}V'\right)^2 \\
&=&\frac{1}{2}m\left\{\left(\frac{m-M}{m+M}\right)^2v'^2+\left(\frac{2M}{m+M}\right)^2V'^2\right\}+\frac{1}{2}M\left\{\left(\frac{2m}{m+M}\right)^2v'^2+\left(\frac{m-M}{m+M}\right)^2V'^2\right\} \\
&=&\frac{1}{2}v'^2\left\{m\left(\frac{m-M}{m+M}\right)^2+M\left(\frac{2m}{m+M}\right)^2\right\}+\frac{1}{2}V'^2\left\{m\left(\frac{2M}{m+M}\right)^2+M\left(\frac{m-M}{m+M}\right)^2\right\} \\
&=&\frac{1}{2}mv'^2+\frac{1}{2}mV'^2
\end{eqnarray}

 

　上式の1行目から2行目に移るところで、\(\frac{1}{2}m\times 2\frac{m-M}{m+M}\frac{2M}{m+M}\)と\(-\frac{1}{2}M\times 2\frac{2m}{m+M}\frac{m-M}{m+M}\)が相殺されていることに注意してください。

 

関連ページ

作図

物理の問題を解く場合、図を描くことは必須と言えます。図を活用することで、考察が進み、その結果ミスを減らすことができます。図を活用する場合の注意点を説明しています。

運動方程式

物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。

モーメントの考え方

力のモーメントについて、基本的注意事項のいくつかを説明しています。

張力

糸につながれたおもりの運動では、糸の張力を考慮します。張力を考える場合のヒントを説明しています。

運動エネルギーと仕事の関係

運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。

力学的エネルギー保存則を考える

力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。

単振動

単振動に関する問題を解くときに必要な知識について説明をしています。

力積

力学は物理の基礎とも柱とも言えます。しっかり勉強して理解を深めましょう。

円運動

円運動を考えるには、向心力を用いて運動方程式を立てるか、遠心力で力のつりあいを考えます。円運動の問題は難しく感じますが、出題のパターンは多くありません。

二体問題　Ⅰ

互いに力を及ぼし合う二つの物体の動きを考えます。