物理の大学入試問題をいかにして解くか

トップページ ＞ 力学 ＞ 二体問題　Ⅰ

 

1．\(x\)軸上を運動する、質量\(m_1\)の物体\(1\)と、\(m_2\)の物体\(2\)からなる系の重心に関する式は、

 

\begin{eqnarray} x_G&=&\frac{m_1x_1+m_2x_2}{m_1+m_2} \tag{2-1} \label{nitai2-1} 　　\\
v_G&=&\frac{m_1v_1+m_2v_2}{m_1+m_2} \tag{2-2} \label{nitai2-2} \\
a_G&=&\frac{m_1a_1+m_2a_2}{m_1+m_2} \tag{2-3} \label{nitai2-3}
\end{eqnarray}

 

ここで、\(x_G\)、\(v_G\)、\(a_G\)は、それぞれ物体1と物体2からなる系の重心の座標と速度と加速度です。
物体1と物体2の座標と速度、加速度を、それぞれ、\(x_1\)、\(x_2\)、\(v_1\)、\(v_2\)、\(a_1\)、\(a_2\)とします。

 

 

２．互いに力を及ぼし合う二つの物体の運動を考える問題を二体問題と呼びます。

 

　二体問題では、二つの物体からなる系の重心の運動と、ひとつの物体から他方を見たときの相対運動とに分けて考えるとわかりやすいです。
　問題によっては、重心から見た二つの物体の相対運動を考えると良いです。

 

 

３．外力がはたらかない場合の二体問題では、

 

　系の重心は静止しているか、等速度運動をしています。
　静止しているか、等速度運動しているかは、特定の時刻の二つの物体の運動量の和から判断します。
運動量の和が\(0\)ならば静止、一定ならば等速度運動です。
　このことは、\(v_G=\frac{m_1v_1+m_2v_2}{m_1+m_2}\)の分子が系の運動量の和であることから導き出されます。

 

 

４．外力として重力だけが働く場合、

 

　重心の運動は、重心に二つの物体の質量があり、そこに重力がはたらいているとして、解くことができます。
　また、重心と一緒に運動している観測者から二つの物体を観測すると、重力がはたらいていないように見えます。

 

 

 

　互いに相互作用を及ぼし合う二つの質点（物体）の運動を考える問題を二体問題と呼ぶことがあります。
ここでは、例を挙げて、二体問題の考察のポイントについて考えます。

 

　次の例題を考えます。

 

　

 

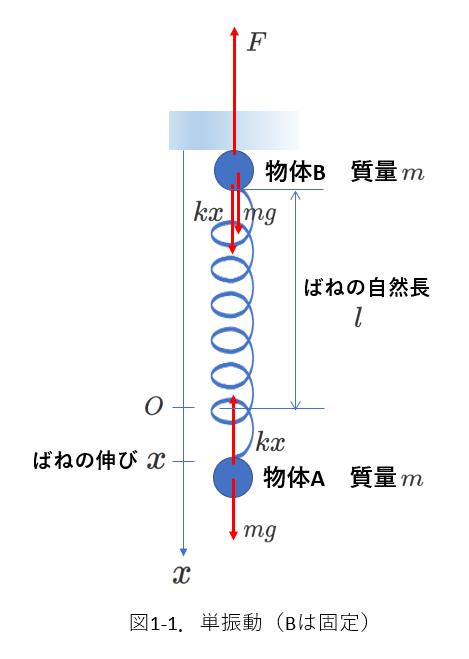
　共に質量が\(m\)の物体Aと物体Bが、ばね定数が\(k\)で質量が無視できるばねでつながれています。

 

　図1-1のように、物体Bが天井に固定されていて、物体Aは鉛直方向に単振動をしています。

 

　ばねが自然長のときのAの位置を原点として、下向き正の\(x\)軸を考えます。

 

　ばねの伸びが\(x\)（Aの座標が\(x\)）であるときに物体A、Bにはたらく力を図示すると、図1-1の赤矢印のようになります。

 

　ばねは伸びているので、ばねの弾性力はばねを縮める向きになります。
そして、物体A,Bは重力\(mg\)を受けています。

 

　物体Bは天井に固定されているのですが、天井がBを支える力の大きさは、\(kx+mg\)に等しくなります。
単振動しているので、ばねの弾性力の大きさは変化しますから、天井がBを支える力も変化することになります。

 

 

 

　さて、いま物体Bを静かに放します。
図1-1において、物体Aが最下点に達したときに物体Bを放す場合を考えましょう。

 

　そして、物体A、ばね、物体Bは鉛直方向にのみ運動をすると考えます。

 

　このとき、物体A、ばね、物体Bからなる系がどのような運動をするか、というのが問題です。

 

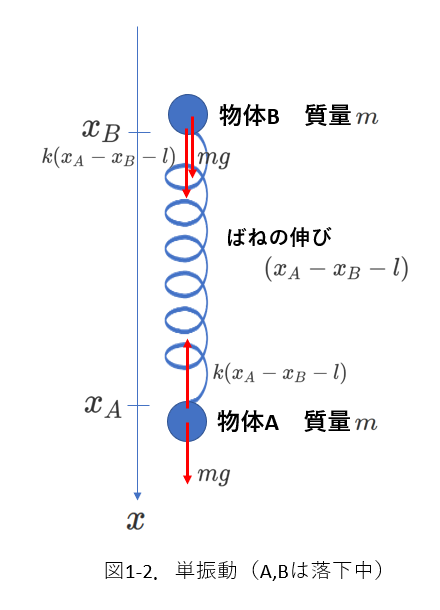
　運動を考えるので、物体に働く力を数え上げ、運動方程式を立てます。

 

　物体A、Bの加速度をそれぞれ、\(a_A\)、\(a_B\)、座標をそれぞれ、\(x_A\)、\(x_B\)とします。（図1-2を参照）
ばねの自然長を\(l\)とすると、ばねの伸びは（\(x_A-x_B-l\)）です。
鉛直下向きを正として、運動方程式は、

 

\begin{eqnarray}
A&:&\ ma_A=mg-k(x_A-x_B-l) \tag{1-1} \label{nitai1-1} \\
B&:&\ ma_B=mg+k(x_A-x_B-l) \tag{1-2} \label{nitai1-2}
\end{eqnarray}

 

　（\ref{nitai1-1})式 + （\ref{nitai1-2})式を考えると、
\begin{equation} m(a_A+a_B)=2mg \tag{1-3} \label{nitai1-3} \end{equation}

 

　これを書き換えると、
\begin{equation} \frac{ma_A+ma_B}{m+m}=g \tag{1-4} \label{nitai1-4} \end{equation}

 

　（\ref{nitai1-4}）式の左辺は、物体ＡとＢからなる系の重心の加速度\(a_G\)を表しています。
そして、\(a_G=g\)　ですから、物体Aと物体Bからなる系の重心は、加速度\(g\)の等加速度運動をすることがわかります。

 

 

　では、次に、(\ref{nitai1-1})式 - (\ref{nitai1-2})式を考えます。　すると、
\begin{eqnarray} m(a_A-a_B)&=&-2k(x_A-x_B-l) \tag{1-6} \label{nitai1-6} \\
a_A-a_B&=&-\frac{2k}{m}(x_A-x_B-l) \tag{1-7} \label{nitai1-7}
\end{eqnarray}

 

　左辺の（\(a_A-a_B\)）は、物体Bから見た物体Aの加速度を表しています。
そして、右辺が、\(-[正の定数]（[Ｂから見たＡの変位]-[定数]）\)となっていることから、Ｂから見てＡは、単振動をすることがわかります。
その角振動数は、\((\ref{nitai1-7})\)式から、\(\sqrt{\frac{2k}{m}}\)です。

 

 

 

 

　（\ref{nitai1-7}）式は、物体Bから見た物体Aの運動を表しています。それでは、重心から見た物体Aの運動はどのように表されるでしょうか。　それには、重心の加速度を\(a_G\)として、（\ref{nitai1-7}）式をもとにして、\(a_A-a_G\)を計算すればよいです。

 

　重心の座標\(x_G\)は、
\begin{equation} x_G=\frac{x_A+x_B}{2} \tag{1-8} \label{nitai1-8} \end{equation}
です。

 

　また、\(a_G=\frac{a_A+a_B}{2}\)ですから、
\begin{eqnarray} a_A-a_G=a_A-\frac{a_A+a_B}{2}&=&\frac{a_A-a_B}{2} \\
\\
（\ref{nitai1-7}）式の右辺のx_Bの代わりにx_G を含む式に書き換えれば&、&良いと考えると、 \\
(\ref{nitai1-8})式から、x_B=2x_G-x_Aを（\ref{nitai1-7}）式に代入して、&& \\
a_A-a_G&=&\frac{a_A-a_B}{2}=-\frac{k}{m}(x_A-(2x_G-x_A)-l) \\
&=&-\frac{2k}{m}\left(x_A-x_G-\frac{l}{2}\right) \tag{1-9} \label{nitai1-9} \\
\end{eqnarray}

 

　つまり、重心から見た物体Aの運動は、Bから見たときと同様に、角振動数が\(\sqrt{\frac{2k}{m}}\)の単振動をすることがわかります。
但し、Bから見たときと重心から見たときでは、物体Aの単振動の振幅は異なります。

 

 

 

 

　以上のことから、二体問題については、系全体の重心の運動と相対運動に分けて考えるのがよさそうです。

 

　基本は運動方程式ですから、二体問題だということを意識しなくても、運動方程式を立てて、これまでの説明のように、考察すれば解けます。

 

　ただその際にも、方程式を重心の運動と相対運動のふたつの式に書き直せることを覚えておくと、スムーズに考察できるでしょう。

 

 

 

１．重心の座標、速度、加速度

 

　重心について整理しておきます。

　

 

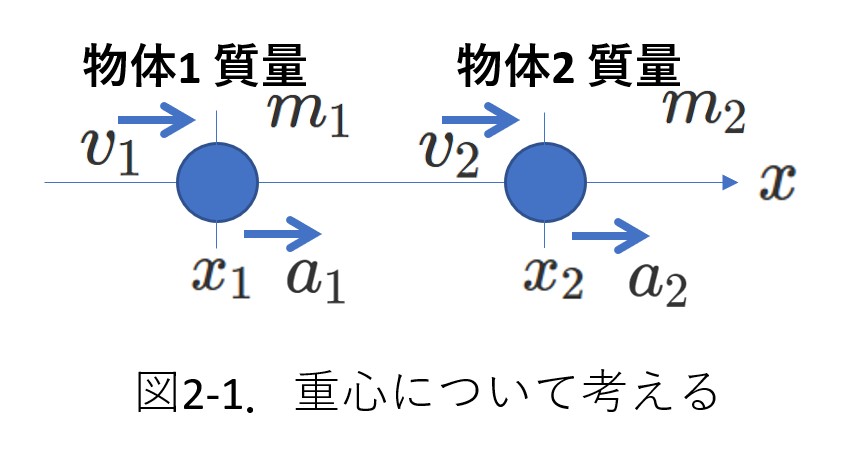
　右図のように、質量\(m_1\)の物体\(1\)と、\(m_2\)の物体\(2\)があります。

 

　簡単にするために、物体1，2とも\(x\)軸上を運動するものとします。
　物体1，2の座標と速度、加速度を、それぞれ、\(x_1\)、\(x_2\)、\(v_1\)、\(v_2\)、\(a_1\)、\(a_2\)とします。
これらはいずれも、物体1、物体2の外側から観察している値です。

 

 

　物体1と物体2からなる系の重心の座標、速度と加速度を、\(x_G\)、\(v_G\)、\(a_G\)とすると、

 

\begin{equation} x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2} \tag{2-1} \label{nitai2-01} \end{equation}

 

 

　（\ref{nitai2-01}）式の両辺を時刻\(t\)で微分すれば、
\begin{eqnarray} \frac{dx_G}{dt}&=&\frac{m_1\frac{dx_1}{dt}+m_2\frac{dx_2}{dt}}{m_1+m_2} \\
v_G&=&\frac{m_1v_1+m_2v_2}{m_1+m_2} \tag{2-2} \label{nitai2-02}
\end{eqnarray}

 

　（\ref{nitai2-02}）式をさらに微分して、
\begin{eqnarray} \frac{dv_G}{dt}&=&\frac{m_1\frac{dv_1}{dt}+m_2\frac{dv_2}{dt}}{m_1+m_2} \\
a_G&=&\frac{m_1a_1+m_2a_2}{m_1+m_2} \tag{2-3} \label{nitai2-03}
\end{eqnarray}

 

　\(x_G\)も\(v_G\)も\(a_G\)も同じ形の式で表されます。

 

 

　さて、（\ref{nitai2-02}）式は大事な式です。
分子が、物体1と物体2の運動量の和になっています。

 

　つまり、運動量保存則がなりたつ場合（言い換えれば、外力が働いていない場合）、重心の速度は一定となります。
さらに、運動量の和が\(0\)となっているときには、重心は静止したまま、動かないということになります。
これは、大事なポイントです。

 

　運動量はベクトル量で、運動量のある方向の成分の和が保存される場合もあります。
このときには、重心の速度のその方向の成分が一定ということになります。
また、運動量のその方向の成分の和が\(0\)の場合には、重心の座標のその方向の成分が一定ということになります。

 

 

 

　さて、物体1と物体2の運動量の和が\(0\)の時、時刻\(t_1\)から時刻\(t_2\)の間に、物体1が\(x_1\)から\(x_1'\)に、物体2が\(x_2\)から\(x_2'\)に、移動したとします。
このときには、重心は静止していますから、時刻\(t_1\)でも時刻\(t_2\)でも重心の座標は変化しません。
　この座標を\(x_G\)とすると、
\begin{eqnarray} x_G&=&\frac{m_1x'_1+m_2x'_2}{m_1+m_2} \tag{2-4} \label{nitai2-04} \\
x_G&=&\frac{m_1x_1+m_2x_2}{m_1+m_2} \tag{2-5} \label{nitai2-05}
\end{eqnarray}
　（\(\ref{nitai2-04}\)）式 - （\(\ref{nitai2-05}\)）式を考えると、
\begin{equation} \frac{m_1(x_1'-x_1)+m_2(x_2'-x_2)}{m_1+m_2}=0 　 \tag{2-6} \label{nitai2-06} \end{equation}
つまり、
\begin{equation} m_1[物体1の変位]+m_2[物体2の変位]=0 　 \tag{2-7} \label{nitai2-07} \end{equation}
となります。　これは、重心が静止しているときに成り立つ式であることに注意しましょう。

 

 

 

 

 

２．「I．二体問題の例題」を一般化する　

 

　

 

 

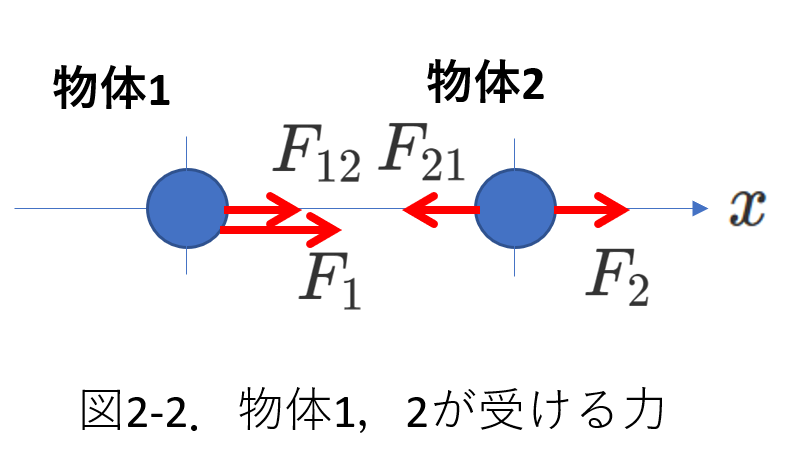
　今、物体1、物体2が右図のような力を受けているとします。
ここで、物体1は物体2に\(F_{21}\)の大きさの力を左向きに及ぼし、物体2は物体1に\(F_{12}\)の大きさの力を右向きに及ぼしているとします。
すなわち、\(F_{12}\)、\(F_{21}\)は内力という設定で、
\begin{equation} F_{12}=F_{21}　　　\tag{2-8} \label{nitai2-08} \end{equation}
です。

 

　また、\(F_1\)と\(F_2\)は外力です。

 

　物体1の質量と物体2の質量を、それぞれ\(m_1\)、\(m_2\)とします。

 

 

　要するに、I．「二体問題の例題」では、\(m_1=m_2=m\)であった問題を\(m_1\neq m_2\)の場合として、また、物体1、物体2が受ける力が重力であったものを、一般的な\(F_1\)、\(F_2\)という力として再検討します。

 

 

　では、運動方程式を立てます。
　ここで、右向きを\(x\)軸の正の向きとしています。
\begin{eqnarray} 物体1&：&\ m_1a_1=F_1+F_{12} \tag{2-9} \label{nitai2-09} \\
物体2&：&\ m_2a_2=F_2-F_{21}　　　　\tag{2-10} \label{nitai2-10}
\end{eqnarray}

 

　[（\(\ref{nitai2-09}\)）式 + （\(\ref{nitai2-10}\)）式]より、
\begin{equation} m_1a_1+m_2a_2=F_1+F_2　　　\end{equation}
(\(\ref{nitai2-03}\))式 \(a_G=\frac{m_1a_1+m_2a_2}{m_1+m_2}\)を用いて、
\begin{equation} (m_1+m_2)a_G=F_1+F_2 \tag{2-11} \label{nitai2-11} \end{equation}

 

　（\(\ref{nitai2-11}\)）式は、
　系の重心の加速度は、重心に物体1と物体2の質量があって、それに外力の合力が働いていると考えて良いことを示しています。

 

 

 

　次に、　（\(\ref{nitai2-09}\)）式と（\(\ref{nitai2-10}\)）式から（\(a_1-a_2\)）を考えます。

 

\begin{eqnarray} a_1-a_2&=&\frac{F_1+F_{12}}{m_1}-\frac{F_2-F_{21}}{m_2} \\
&=&\left(\frac{1}{m_1}+\frac{1}{m_2}\right)F_{12}+\frac{F_1}{m_1}-\frac{F_2}{m_2} \tag{2-12} \label{nitai2-12}
\end{eqnarray}

 

　ここで、次のように、換算質量\(\mu\)を導入すると、
\begin{equation} \mu=\frac{m_1m_2}{m_1+m_2} 　、　　　　　　　\frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2} \tag{2-13} \label{2-13} \end{equation}
(\(\ref{nitai2-12}\))式は、
\begin{eqnarray} a_1-a_2&=&\frac{1}{\mu}F_{12}+\frac{F_1}{m_1}-\frac{F_2}{m_2} \\
\mu a_{12}=\mu(a_1-a_2)&=&F_{12}+\frac{\mu}{m_1}F_1-\frac{\mu}{m_2}F_2 \tag{2-14} \label{nitai2-14}
\end{eqnarray}
（\(a_{12}\)は物体2から物体1を見たときの加速度（相対加速度）です。）

 

　この式は少々複雑なので、「Ⅰ．二体問題の例題」と同じに、\(F_1\)、\(F_2\)が重力である場合を考えましょう。
\(F_1=m_1g、F_2=m_2g\)であるので、（\(\ref{nitai2-14}\)）式は、
\begin{equation} \mu(a_1-a_2)=F_{12} \tag{2-15} \label{nitai2-15} \end{equation}
と変形できます。

 

　この式の意味するところは、
換算質量に内力がはたらいといるとして相対加速度を求めることができることです。

 

 

　｛（\(\ref{nitai2-09}\)）式、（\(\ref{nitai2-10}\)）式｝と｛（\(\ref{nitai2-11}\)）式、（\(\ref{nitai2-14}\)）式｝は等価ですから、｛\(a_1\)、\(a_2\)｝と｛\(a_G\)、\(a_{12}\)｝も等価です。

 

 

 

 

 

　系の重心の運動と相対運動がわかったら、外部から見た、物体1と物体2の運動を知りたいですね。
そこで、\(a_G\)、\(a_{12}\)が得られたとして、これらの値から、\(a_1\)、\(a_2\)を求めてみましょう。

 

　それには、（\(\ref{nitai2-03}\)）式と（\(\ref{nitai2-14}\)）式を考えます。
\begin{eqnarray}
a_G&=&\frac{m_1a_1+m_2a_2}{m_1+m_2} \tag{\ref{nitai2-03}} \\
a_{12}&=&a_1-a_2 \tag{\ref{nitai2-14}}
\end{eqnarray}
　これらの式は、\(a_1\)と\(a_2\)を未知数とする連立方程式と捉えることができます。
　（\(\ref{nitai2-14}\)）式を、\(a_2\)に関する式に変形し、 （\(\ref{nitai2-03}\)）式に代入します。
\begin{eqnarray} a_G&=&\frac{m_1a_1+m_2(a_1-a_{12})}{m_1+m_2} \\
&=&\frac{(m_1+m_2)a_1}{m_1+m_2}-\frac{m_2a_{12}}{m_1+m_2} \\
&=&a_1-\frac{m_2a_{12}}{m_1+m_2} \\
a_1&=&a_G+\frac{m_2a_{12}}{m_1+m_2} \tag{2-16} \label{nitai2-16}
\end{eqnarray}　
　（\ref{nitai2-14}）式と（\ref{nitai2-16}）式から、
\begin{equation} a_2=a_G-\frac{m_1a_{12}}{m_1+m_2} \tag{2-17} \label{nitai2-17} \end{equation}

 

　さて、
\begin{eqnarray}
[床から見た物体1の加速度a_1]&=&[床から見た重心の加速度a_G]+[重心から見た物体1の加速度a_{1G}]　　\tag{2-18} \label{nitai2-18} \\
[床から見た物体2の加速度a_2]&=&[床から見た重心の加速度a_G]+[重心から見た物体2の加速度a_{2G}] \tag{2-19} \label{nitai2-19}
\end{eqnarray}
という関係があるはずですから、（\(\ref{nitai2-16}\)）式と（\(\ref{nitai2-17}\)）式の第二項は、それぞれ、\(a_{1G}\)、\(a_{2G}\)です。

 

　一応確認します。
\begin{eqnarray} [重心から見た物体1の加速度：a_{1G}]=a_1-a_G&=&a_1-\frac{m_1a_1+m_2a_2}{m_1+m_2} \\
&=&\frac{m_2(a_1-a_2)}{m_1+m_2} \\
&=&\frac{m_2a_{12}}{m_1+m_2}
\end{eqnarray}

 

 

 

 

　まとめます。
　二体問題では、それぞれの物体についての運動方程式を立てることができます。
しかし、直接その運動方程式から二つの物体の運動を議論するのは難しいので、代わりに、二体の重心の運動と、物体の一方から見た他方の運動を考えるとよいです。
問題に依っては、（物体の一方から見た他方の運動よりも）重心から見た物体の運動を考えるほうが考察しやすいという場合があります。

 

　（\(\ref{nitai2-11}\)）,（\(\ref{nitai2-14}\)）を公式のように暗記する必要はありません。
二体問題に関する多くの問題では、設問によって誘導されますから、これまでの考え方の流れだけ覚えておけば、誘導を予想しながら解くことができます。

 

 

 

 

 

　ここで、「Ⅰ．二体問題の例題」を重心の運動と相対運動の観点から解いてみます。

　この問題では、重心は物体Aと物体Bの位置を結ぶ線分の中点にあります。

 

　そして、重心の加速度は、重力加速度であることが想像されます。

 

　厳密に検討するには、（\(\ref{nitai2-11}\)）の重心に関する運動方程式を立てて、
\begin{eqnarray} (m_1+m_2)a_G&=&F_1+F_2 \tag{\ref{nitai2-11}} \\
(m+m)a_G&=&mg+mg \\
a_G=g
\end{eqnarray}
　と考えれば良いです。

 

 

 

　そして、次に、重心から見た、物体Ａと物体Ｂの運動を考えます。

 

　重心は加速度運動をしていますから、重心から物体Ａと物体Ｂを観察すると、両者には慣性力がはたらきます。
その大きさは\(mg\)です。

 

　このときに、物体Aと物体Bにはたらく力を図示すると、図2-3のようになります。

 

 

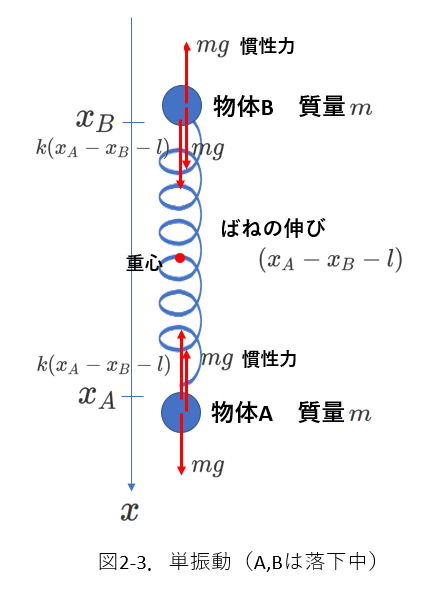
　物体Aにも物体Bにも、同じ大きさの重力（\(mg\)）と慣性力（\(mg\)）がはたらいていて、それらは相殺されます。
結局、重心から見たとき、物体Aにも物体Bにもばねの弾性力だけがはたらいているように見えます。
つまり、物体Aも物体Bも単振動をします。

 

　重心から見ているので、重心は静止しているように見えます。
そして、重心から物体A、物体Bにばねが繋がっています。
　ばねの自然長が半分の\(\frac{l}{2}\)になったわけですから、ばね定数は\(k\)ではなく,\(2k\)になります。
（ばねの長さが半分になったので、同じ力によるばねの伸縮量も、半分になります。
　これは、ばねが固くなったことを意味します。）

 

　物体Bの単振動の角振動数は、質量が\(m\)でばね定数が\(2k\)ですから、\(\sqrt{\frac{2k}{m}}\)となります。
　これは、「Ⅰ．二体問題の例題」の結果と一致します。

 

 

　さて、固定してあった物体Bを、自然長が\(l\)のばねの伸びが最大値\(\Delta l\)になったときに、放したとします。
このときを、時刻\(t\)=0とします。
また、図1-1とは異なり、原点を\(t=0\)のときの物体Bの位置として、下向き正の\(x\)軸を考えます。

 

　これまでの考察から、任意の時刻\(t\)での物体Aの座標を求めます。

 

　重心の座標を\(x_G\)とすると、重心の時刻\(t\)での座標\(x_G\)は、
\begin{equation} x_G=\frac{1}{2}gt^2+\frac{l}{2}+\frac{\Delta l}{2} \tag{2-22} \label{nitai2-22-1} \end{equation}

 

　重心から見た物体Aの位置（相対座標\(x_{AG}\)）は、
時刻\(t=0\)で最大の伸びで、そこからばねは縮み始めます。
つまり、単振動は振幅が\(\frac{\Delta l}{2}\)で、\(+cos\)型ですから、
\begin{equation} x_{AG}=\frac{\Delta l}{2}cos\left(\sqrt{\frac{2k}{m}}t\right)+\frac{l}{2} \tag{2-23} \label{nitai2-23-1} \end{equation}
　単振動は、重心から\(+\frac{l}{2}\)のところを中心にして振動することに注意しましょう。

 

　以上より、\(x_A\)は、
\begin{eqnarray} x_A&=&x_G+x_{AG} \\
&=&\frac{1}{2}gt^2+\frac{l}{2}+\frac{\Delta l}{2}+\frac{\Delta l}{2}cos\left(\sqrt{\frac{2k}{m}}t\right)+\frac{l}{2} \\
&=&\frac{1}{2}gt^2+\frac{\Delta l}{2}cos\left(\sqrt{\frac{2k}{m}}t\right)+l+\frac{\Delta l}{2} \tag{2-24} \label{nitai2-24-1} \end{eqnarray}

 

 

　

 

 

　３．運動量と運動エネルギーについて

 

　前の節では、それぞれの物体の加速度の代わりに、重心の加速度と一方から他方を見たときの加速度を用いて考察できることを説明しました。

 

　ここでは、運動量と運動エネルギーについて、議論します。

 

注意するのは、以下で考察するのは、重心の速度と相対速度を使って、外から見たときのふたつの物体の運動量と運動エネルギーそれぞれの和を、求める方法です。

 

 

　加速度について考えた次の式に対応させて、
\begin{eqnarray}
a_G&=&\frac{m_1a_1+m_2a_2}{m_1+m_2} \tag{\ref{nitai2-03}} \\
a_{12}&=&a_1-a_2 \tag{\ref{nitai2-14}}
\end{eqnarray}
　次の式を考えます。
\begin{eqnarray}
v_G&=&\frac{m_1v_1+m_2v_2}{m_1+m_2} \tag{2-25} \label{nitai2-22} \\
v_{12}&=&v_1-v_2 \tag{2-26} \label{nitai2-23}
\end{eqnarray}
　\(v_1、v_2、v_G、v_{12}\)は、それぞれ、物体1の速度、物体2の速度、物体1と2からなる系の重心の速度、物体2から見た物体1の速度(物体2に対する物体1の相対速度）です。

 

　そして、（\(\ref{nitai2-16}\)）式と（\(\ref{nitai2-17}\)）式を導いたと同様の式変形により、
\begin{eqnarray} v_1&=&v_G+\frac{m_2v_{12}}{m_1+m_2} \tag{2-27} \label{nitai2-24} \\
v_2&=&v_G-\frac{m_1v_{12}}{m_1+m_2} \tag{2-28} \label{nitai2-25}
\end{eqnarray}

 

 

　ここで、運動量を考えます。
\(v_1\)と\(v_2\)から求まる運動量に（\(\ref{nitai2-24}\)）式と（\(\ref{nitai2-25}\)）式を代入します。
\begin{eqnarray} m_1v_1+m_2v_2&=&m_1\left(v_G+\frac{m_2v_{12}}{m_1+m_2}\right)+m_2\left(v_G-\frac{m_1v_{12}}{m_1+m_2}\right) \\
&=&(m_1+m_2)v_G \tag{2-29} \label{nitai2-26}
\end{eqnarray}
　つまり、運動量の和は、質量\(m_1\)と\(m_2\)が系の重心にあると考えたときの、重心の運動量に等しいです。

 

 

　次に、運動エネルギーの和は、
\begin{eqnarray} \frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1\left(v_G+\frac{m_2v_{12}}{m_1+m_2}\right)^2+\frac{1}{2}m_2\left(v_G-\frac{m_1v_{12}}{m_1+m_2}\right)^2 \\
=\frac{1}{2}(m_1+m_2)v_G^2+\frac{1}{2}\left(\frac{m_1m_2}{m_1+m_2}\right)v_{12}^2+\frac{1}{2}2v_G\frac{m_1m_2}{m_1+m_2}v_{12}-\frac{1}{2}2v_G\frac{m_1m_2}{m_1+m_2}v_{12} \\
=\frac{1}{2}(m_1+m_2)v_G^2+\frac{1}{2}\left(\frac{m_1m_2}{m_1+m_2}\right)v_{12}^2 \tag{2-30} \label{nitai2-27} \\
=\frac{1}{2}(m_1+m_2)v_G^2+\frac{1}{2}\mu v_{12}^2
\end{eqnarray}
　この式の\(\mu\)は換算質量です。

 

　この式は、運動エネルギ―の和は、重心に\(m_1+m_2\)の質量があったときの運動エネルギー（重心の運動エネルギー）と換算質量と相対速度から計算した運動エネルギー（相対運動のエネルギー）の和で表されるということです。

 

　これらの運動量やエネルギーに関する式ついても覚える必要はありません。
こんなことが考えられる、という程度に意識しておけば良いです。

 

 

 

　ここでは、二つの物体が接して運動している場合を考えます。
いずれも良く見る設定です。

 

１．斜面を滑る物体（1）

 

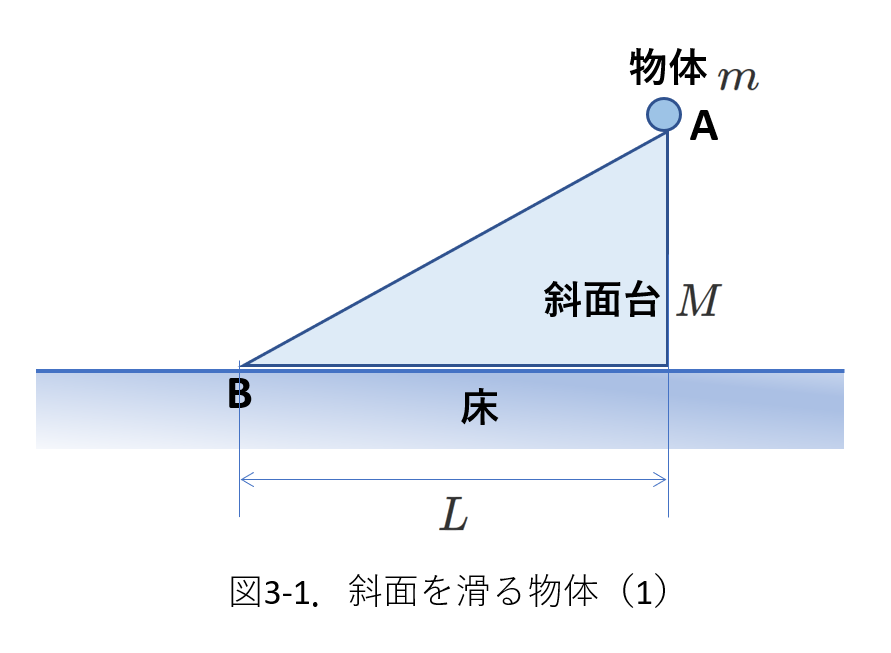
　最初は、右図3-1です。
　床の上に図のような斜面台があって、さらにその上に物体が乗っています。
斜面台の底面の長さは\(L\)です。
　床と斜面台の間と、物体と斜面台の間には摩擦はありません。

 

 

　最初、斜面台も物体も静止している状態から、物体を斜面台の頂上で放し、頂上から斜面台の下まで進む間に斜面台が床の上を移動する距離\(X\)を求めます。

 

　先ず行うことは、物体と斜面台がどのような運動をするのかイメージすることです。
そのためには、運動している途中で、物体と斜面台に働く力を考えます。

 

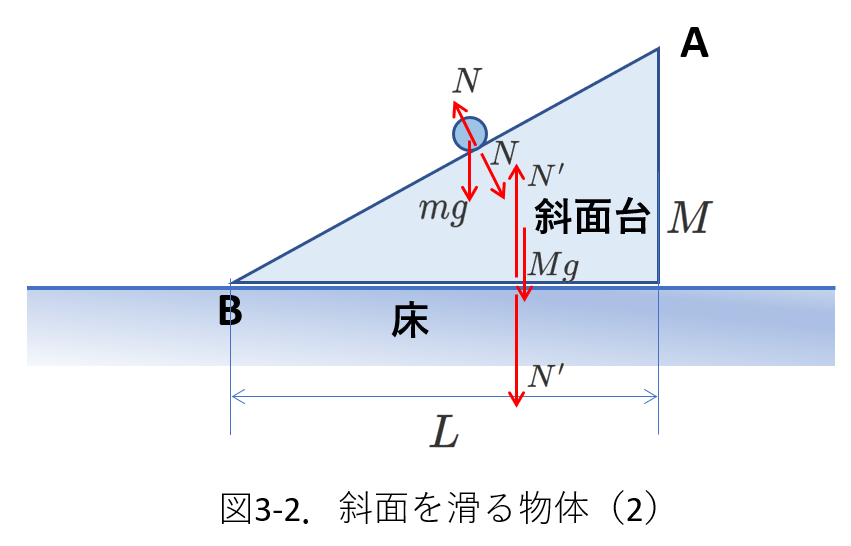
　物体と斜面台にはたらく力を描くと図3-2のようになります。
物体には、斜面台からの垂直抗力\(N\)と重力\(mg\)がはたらきます。
この合力によって、物体は斜面台の斜面を滑り降ります。
斜面台には、物体からの垂直抗力\(N\)と重力\(Mg\)と床からの垂直抗力\(N'\)がはたらきます。

 

　斜面台は床の上を水平方向にしか動かないので、3つの力の鉛直成分はつり合っています。
（あるいは、合力の鉛直方向成分は\(0\)です。）

 

　つまり物体を点Aで放すと、物体は斜面を滑り降り、斜面台は物体からの抗力\(N\)の水平成分により、右向きに動きます。
大体の動きを押さえたところで、動いた前後の図を描いてみます。
これを、図3-3に示します。

 

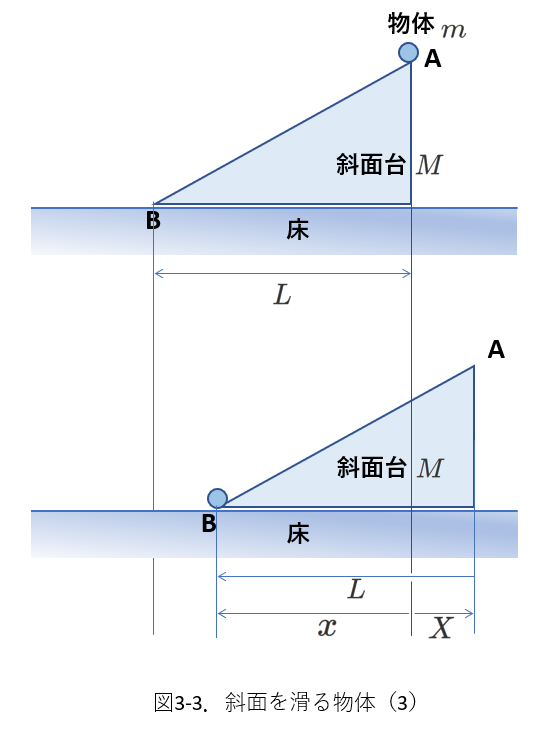
　図で、斜面台は右に、物体は斜面台を滑って、左向きに動きます。

 

　さて、この問題では、物体と斜面台の運動量の水平成分が保存されます。
ということは、物体と斜面台からなる系の重心の速度の水平成分は一定で、変化しません。
　さらに、初期状態で物体も斜面台も静止している（系の重心の速度は\(0\)である）ことから、運動中の系の重心の速度の水平成分も\(0\)で、重心の位置の水平成分は変化しないことがわかります。

 

　図3-3からわかるように、求めるべき、斜面台が動いた距離\(X\)と、床に対して物体が動いた距離\(x\)と、斜面台に対して物体が動いた距離\(L\)の間には、
\begin{equation} x+X=L \tag{3-1} \label{nitai3-01} \end{equation}
の関係があります。

 

　座標の水平成分に関して、「系の重心の位置が変化していない」ことから、[物体が\(A\)にあるときの系の重心の座標]=[物体が\(B\)の位置に達した時の系の重心の座標]という式を立てます。

 

　水平方向に右向きの\(x\)軸を考え、物体と斜面台の重心の初期状態での\(x\)座標を、それぞれ、\(x_1\)、\(x_2\)とします。
最終の状態では、それぞれの重心の\(x\)座標は、\(x_1-x\)、\(x_2+X\)に変化するので、（\ref{nitai3-01}）を用いて変形すると、
\begin{eqnarray} \frac{mx_1+Mx_2}{m+M}&=&\frac{m(x_1-x)+M(x_2+X)}{m+M} \tag{3-2} \label{nitai3-02} \\
\frac{mx_1+Mx_2}{m+M}&=&\frac{m(x_1-L+X)+M(x_2+X)}{m+M} \tag{3-3} \label{nitai3-03} \\
X&=&\frac{m}{m+M}L \tag{3-4} \label{nitai3-04}
\end{eqnarray}
　（\ref{nitai3-02}）式を書き直すと、
\begin{eqnarray}
\frac{mx_1+Mx_2}{m+M}&=&\frac{m(x_1-x)+M(x_2+X)}{m+M} \tag{3-2} \\
\frac{m(-x)+MX}{m+M}&=&0 \\
m(-x)+MX&=&0 \tag{3-5} \label{nitai3-05} \end{eqnarray}
　つまり、物体と斜面台の変位に（\(\ref{nitai3-05}\)）式の関係が成り立ち、これと、（\(\ref{nitai3-01}\)）式とから直ちに\(X\)が求まります。
　（\(\ref{nitai3-05}\)）式は、（\(\ref{nitai2-06}\)）（\(\ref{nitai2-07}\)）式と同じものです。

 

　以上のように、重心が水平方向には動かないという考えから、物体と斜面台の移動距離が簡単に求められることがわかりました。

 

 

 

 

 

 

２．箱の中の振り子

 

 

 

 

 

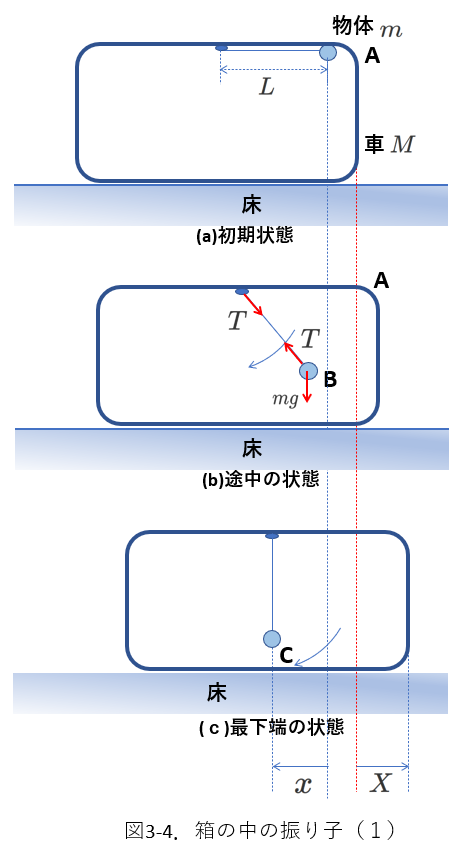
　次の例は図3-4です。

 

　内側が空洞の、質量が\(M\)の箱の中に、天井から長さ\(L\)の糸で吊るされた質量\(m\)の物体があります。
糸をぴんと張った状態で物体を天井まで持ち上げ(a)、静かに放します。
箱は床の上に置かれていて、箱と床の間には摩擦はありません。
また、物体の体積は十分に小さいものとします。

 

　手を放してから、物体が、糸を天井に固定している点の真下にきたときまでに、箱が移動した距離\(X\)を求めます。

 

　図3-4の(b)に、運動中に物体と箱が受ける力が表されています。
物体と箱は糸を介して、糸の張力を及ぼしあっています。
この力は、大きさが同じで向きが逆ですから、物体と箱の系にとっては内力です。
また、物体には鉛直方向に外力である重力\(mg\)がはたらいています。
　以上より、物体と箱の運動量の水平成分が保存されることがわかります。
（鉛直方向には、物体に重力がはたらくため、運動量の鉛直成分の和は保存されません。）

 

 

 

 

 

 

　また、(a)の初期状態には、物体も箱も静止しているので、物体と箱からなる系の重心の座標の水平成分は変化しません。

 

　物体と箱の変位をそれぞれ\(x\)、\(X\)とします。
右向きを正とすれば、物体は左向きに、箱は右向きに変位するので、\(x\lt 0\)、\(X\gt 0\)です。
（前問（図3-2）では移動した距離を考えましたが、ここでは変位を考えていることに注意しましょう。）

 

　したがって、（\ref{nitai3-05}）式の導出と同様に考えれば、
\begin{equation} \frac{mx+MX}{m+M}=0 \tag{3-7} \label{nitai3-07} \end{equation}

　

（\ref{nitai3-05}）式と符号が異なることを確認しましょう。

 

 

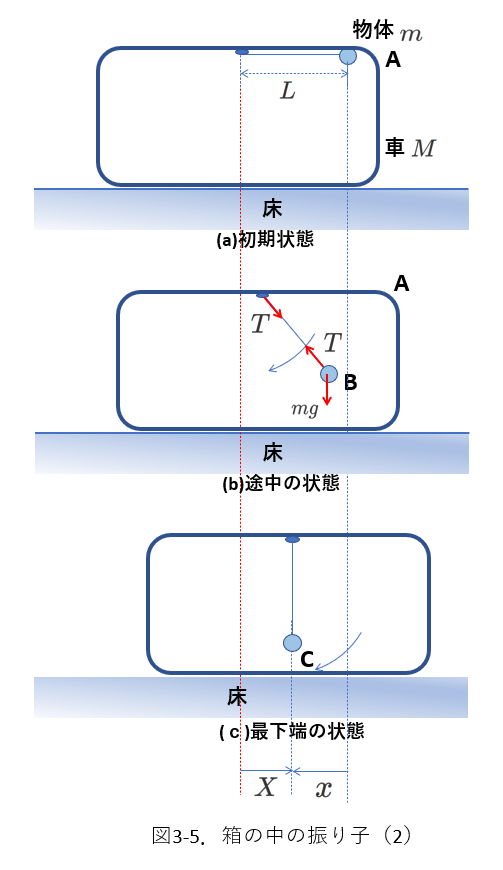
　もうひとつ\(x\)と\(X\)の関係を表す式が必要ですが、図3-4では少々わかりにくいです。

 

　この図を、図3-5のように書き換えてみました。
　これだとよくわかりますね。
\begin{equation} X-x=L \tag{3-8} \label{nitai3-08} \end{equation}
（\(x\)の負号に注意しましょう。）

 

 

　（\(\ref{nitai3-07}\)）式と（\(\ref{nitai3-08}\)）式から、
\begin{eqnarray} \frac{m(X-L)+MX}{m+M}&=&0 \\
X=\frac{m}{m+M}L \tag{3-9} \label{nitai3-09}
\end{eqnarray}

 

 

 

 

 

 

 

 

 

 

 

 

 

３．斜面を滑る物体（2）

 

　もうひとつの例題を図3-6に示します。

 

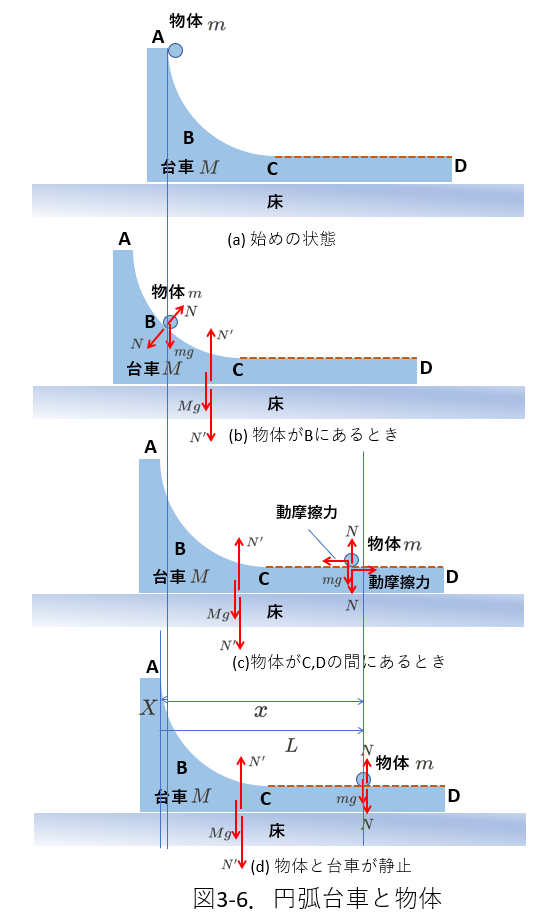
　床の上に、図のような断面形状を持つ質量\(M\)の台車、そして、その上に質量\(m\)の物体が乗っています。
台車と床の間には摩擦はありません。
物体と台車の間には、点Cから点Dまでには摩擦がはたらきます。

 

　初期状態で、物体も台車も静止していて、物体は点Aで支えられています。
今静かに物体を放したところ、物体は台車の表面を右向きに滑り降り、台車は左向きに移動しました。
点Cから物体には動摩擦力がはたらき、物体は台車に対して静止しました。

 

　このとき、物体は点Ａから水平方向に距離\(L\)だけ移動していたとして、台車の変位を求めるのが問題です。

 

　問題を解く手順は、１．受ける力をすべて図示する　２．運動をイメージする　３．運動方程式を立てる　です。
３．では運動方程式の代わりに、運動量保存の式や力学的エネルギー保存の式を立てる場合もあります。

 

　図3-6(b)には、物体が点Aから点Cに滑り降りる途中で、物体と台車にはたらく力を図示してあります。

 

　物体と台車は、垂直抗力\(N\)の力を及ぼし合います。
この大きさは同じで向きが逆ですから、内力です。

 

　台車と床も垂直抗力\(N'\)の力を及ぼしあっています。
　また、物体にも台車にも重力がはたらいています。

 

　運動をイメージします。

 

　物体が\(A\)から\(C\)に動く間、台車は物体から抗力\(N\)を受けます。
また、物体も同じ大きさで向きが逆の垂直抗力\(N\)を受けます。
この力によって、台車は左向きに動きます。
水平成分を含む力は、これだけなので、物体と台車からなる系の運動量の水平成分は保存されます。

 

　初期状態で物体も台車も静止していることから、物体が点Aから点Cに動く間、物体と台車からなる系の重心の位置は水平方向には変化しません。

 

　前のふたつの例題を考えると、物体が点Cに達したときの、台車の変位を計算することができます。

 

　では、物体が点Cから点Dに動く間はどうでしょう。
　ここでは、動摩擦力がはたらきます。

 

　物体にはたらく動摩擦力と、台車にはたらく動摩擦力は大きさが同じで向きが逆です。
つまり、このときも、物体と台車の運動量は保存されます。

 

　摩擦力が関与すると力学的エネルギーは保存されないので、運動量も保存されないように考えてしまいますが、この場合、動摩擦力が物体に与える力積と、台車に与える力積は、大きさが同じで向きが逆ですから、物体と台車からなる系を考えると、２つの力積は相殺されることから、物体と台車の運動量の和を考えると一定であることがわかります。

 

　以上より、この運動の全てで運動量が保存されていることがわかりました。

 

　そこで、物体が台車に対して静止したときの、床に対する物体の速度を\(V\)とすれば、床に対する台車の速度も\(V\)です。
運動量保存則を適用すると、
\begin{eqnarray} m\cdot 0+M\cdot 0&=&mV+MV \tag{3-10} \label{nitai3-10} \\
V&=&0
\end{eqnarray}
つまり、物体も台車も、最終的には静止することが分かりました。

 

　床に対する台車の変位を\(X\)とします。
右向きを正として、台車は左に変位したと考えているのでて、\(X\lt 0\)です。
すると、床に対する物体の変位\(x\)は、\(x=L+X\) ですから、
\begin{eqnarray} \frac{m(L+X)+MX}{m+M}&=&0 \\
X&=&-\frac{m}{m+M}L \tag{3-11} \label{3-11}
\end{eqnarray}

 

　\(X\)が負号を持つのは、台車は左向きに変位したことを意味しています。

 

 

 

　ここでは、二つの物体がばね等でつながれている場合を考えます。

 

 

１．ばねでつながった二体の運動

 

 

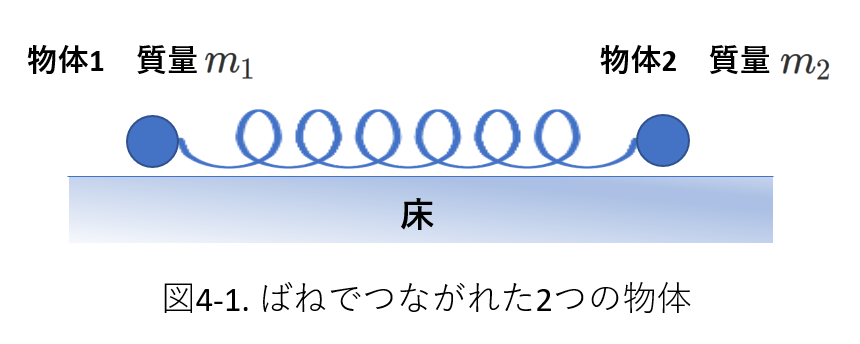
　最初の例は、右の図4-1です。

 

　質量\(m_1\)と\(m_2\)のふたつの物体が、ばね定数\(k\)の非常に軽いばねに繋がれて、床の上に置かれています。
この状態ではばねは自然長ですが、これに水平方向の力をかけて\(x\)だけ伸ばします。

 

　そして、同時にふたつの物体を放すと、どちらも単振動を始めました。
このときばねのある一点は、動かず、静止しています。

 

　この点が重心であることを導くのが問題です。
　（ちなみにこれは東京都立大学の問題です。）

 

　最初に、それぞれの物体にはたらく力を確認します。
それが図4-2です。

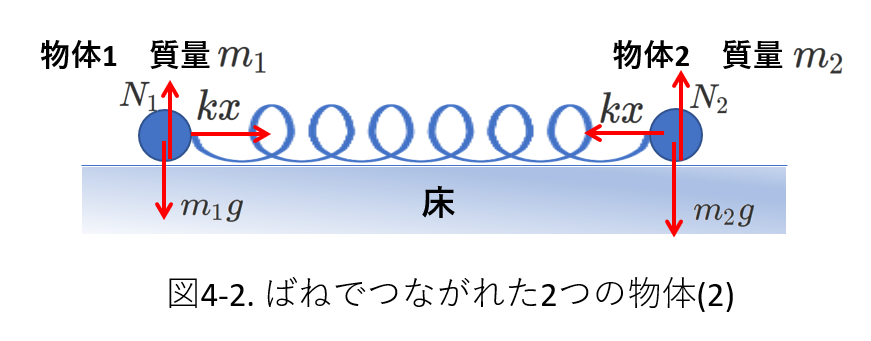
物体には、床に垂直に垂直抗力\(N_1\)、\(N_2\)と重力\(m_1g\)、\(m_2g\)がはたらきますが、この方向に物体は動かないので、ふたつの力はつり合っています。

 

　水平方向に働く力は、ばねの弾性力だけです。
この力はふたつの物体とばねからなる系を考えたとき内力です。
外力は水平方向には働いていません。

 

 

 

［解1］

 

　これまで考えてきたことを元にすると、
ふたつの物体からなる系の重心は、静止しているか、等速直線運動をしていると考えることができます。
　ふたつの物体を放した直後は、系の重心は静止しているとみなせるので、それ以降も重心は静止していることになります。

 

 

　これまでの重複になりますが、これを式で表してみましょう。

 

 

 

　それぞれの物体の加速度の水平成分を\(a_1\)、\(a_2\)で表し、右向きを正とすると、運動方程式は、
\begin{eqnarray} m_1a_1&=&kx　　　　　　\tag{4-1} \label{nitai4-01} \\
m_2a_2&=&-kx \tag{4-2} \label{nitai4-02}
\end{eqnarray}
です。

 

　上の2式の両辺同士の和をとると、
\begin{eqnarray} m_1a_1+m_2a_2=0 \tag{4-3} \label{nitai4-3} \\
\\
\frac{m_1a_1+m_2a_2}{m_1+m_2}=0 \tag{4-4} \label{nitai4-04}
\end{eqnarray}
となります。

 

　（\ref{nitai4-04}）式は、重心の加速度が\(0\)であることを示しています。
このことは、重心は静止しているか、等速直線運動をしていることになり、ふたつの物体を放した直後は重心も静止していることから、重心はその後も静止しているとわかります。

 

 

　さて、以上の議論でわかったのは、「重心は静止している」ということですが、問題が求めているのは、「静止している点は重心である」ことです。
したがって、「重心以外の点はすべて動いている」ことを説明しておかないと、問題を解いたことになりません。

 

　重心から、左右を観察すれば、どちらの物体も単振動をしていますから、ばねのどの部分も静止している点はありません。
したがって、「重心は静止、それ以外の点はすべて動いていることから、静止している点は重心」と結論ができます。

 

 

 

［解2］

 

　東京都立大の問題では、設問に従って、別の方法で解くように誘導されています。

 

　その方法とは、「静止している点は、全ての時刻においてその点が受ける力がつり合っている（あるいは合力が\(0\))」と考えることです。

 

 

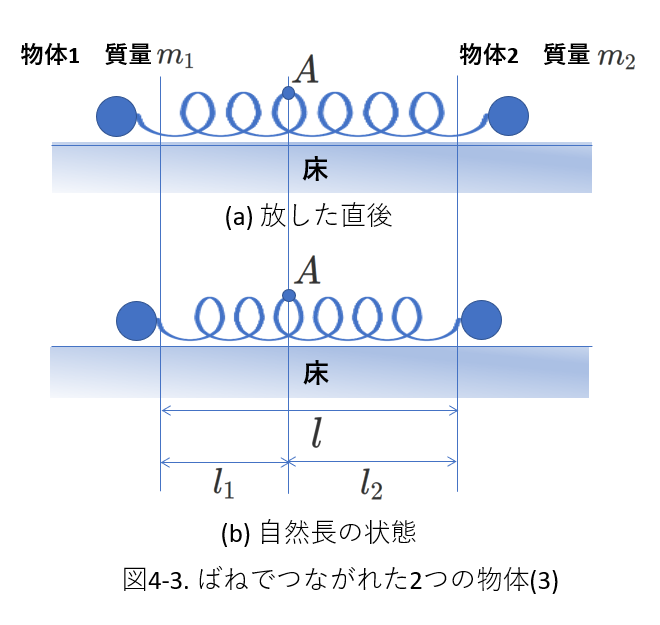
　図4-3を見てください。
今、そのような点がＡであったとします。
点Aはどの時刻でも静止している点です。

 

　ばねが伸びている状態では、点Ａには、左向きに、ばねの左部分による弾性力がはたらきます。　
同時に、右向きに、ばねの右部分による弾性力がはたらきます。

 

　どちらの物体も単振動をしているので、それらの弾性力は時刻によって変化します。
すべての時刻で力がつり合うことを考えるのであれば、このことも考慮する必要があります。

 

　それでは、まず、その弾性力を求めます。
弾性力ですから、ばね定数と伸びを知る必要があります。
まず点Aをどのように表すかですが、ばねの自然長を\(l\)として、自然長のばねの左端から\(l_1\)、右端から\(l_2\)の距離にあると仮定します。

 

　次に、ばね定数ですが、長さ\(l\)のばねのばね定数が\(k\)です。
その長さが\(l_1\)、\(l_2\)となったので、ばね定数は、
\begin{eqnarray}
左側が、k_1&=&k\frac{l}{l_1}　　　\tag{4-5} \label{nitai4-05} \\　　
右側が、k_2&=&k\frac{l}{l_2} \tag{4-6} \label{nitai4-06}
\end{eqnarray}
となります。
（ばねは一様であると仮定しています。）

 

 

　ばねの全体の伸びを\(x\)とすれば、左側の伸びは、\(\frac{l_1}{l}x\)、右側の伸びは\(\frac{l_2}{l}x\)ですから、
弾性力は、左側が\(k\frac{l}{l_1}\frac{l_1}{l}x=kx\)、右側が\(k\frac{l}{l_2}\frac{l_2}{l}x=kx\)となります。

 

 

　困った結果が出てしまいました。
なぜなら、このことは、ばねの伸びがいくらであっても、点Ａがどこであっても、時刻がいつであっても、常に左右の力がつり合っていることを示しているからです。

 

　これは、ばねの質量を無視したことから起きたことです。

 

 

 

　このような議論を避けるために、問題は、別の方向（角振動数）から考えるように誘導しています。

 

　点Aから左側のばねの振動の角振動数を\(\omega_1\)、右側のばねの角振動数を\(\omega_2\)として、(4-5)(4-6)式を用いてこれらを求めます。
\begin{eqnarray} \omega_1=\sqrt{\frac{k_1}{m_1}}=\sqrt{\frac{kl}{m_1 l_1}} \tag{4-7} \label{nitai4-07} \\
\omega_2=\sqrt{\frac{k_2}{m_2}}=\sqrt{\frac{kl}{m_2 l_2}} \tag{4-8} \label{nitai4-08}
\end{eqnarray}

 

　ふたつの物体を放した直後のばねののびを\(d\)、その時刻を\(t=0\)として、左右の物体の時刻\(t\)の伸びをそれぞれ\(X_1\)、\(X_2\)とすると、
\begin{eqnarray} X_1=\frac{l_1 d}{l}\cos{\omega_1 t} \\
X_2=\frac{l_2 d}{l}\cos{\omega_2 t}
\end{eqnarray}

 

　そこで、左右の力が等しいと言う式を立てると、
\begin{eqnarray} k_1 X_1&=&k_2 X_2 \\
\frac{kl}{l_1}\frac{l_1 d}{l}\cos (\omega_1 t)&=&\frac{kl}{l_2}\frac{l_2 d}{l}\cos (\omega_2 t) \\
kd\cos (\omega_1 t)&=&kd\cos (\omega_2 t)
\end{eqnarray}

 

　したがって、\(\omega_1=\omega_2\)となり、
\begin{equation} m_1l_1=m_2l_2 \tag{4-9} \label{nitai4-09}　 \end{equation}
が、得られます。

 

　ばねが自然長のときの、物体1から重心までの距離を\(b\)とすると、
\begin{eqnarray} b&=&\frac{m_1 0+m_2l}{m_1+m_2}=\frac{m_2l_1+m_2l_2}{m_1+m_2} \\
(\ref{nitai4-09})式より、b&=&\frac{m_2 l_1+m_1 l_1}{m_1+m_2}=l_1
\end{eqnarray}

 

　つまり、点Aは重心に相当することがわかりました。

 

 

 

 

［変形問題］

 

　前問を少し変形して別の問題として考えてみます。
　前問と逆に、重心から見た物体1と物体2が同じ角振動数で単振動することを示します。

 

［解1］

 

　重心が静止していることから、その左右に長さ\(l_1\)、\(l_2\)のばねがあるものとしてそのばねとおもりの系の角振動数を求めます。
それには、(\ref{nitai4-07})、(\ref{nitai4-08})式が使えます。

 

 

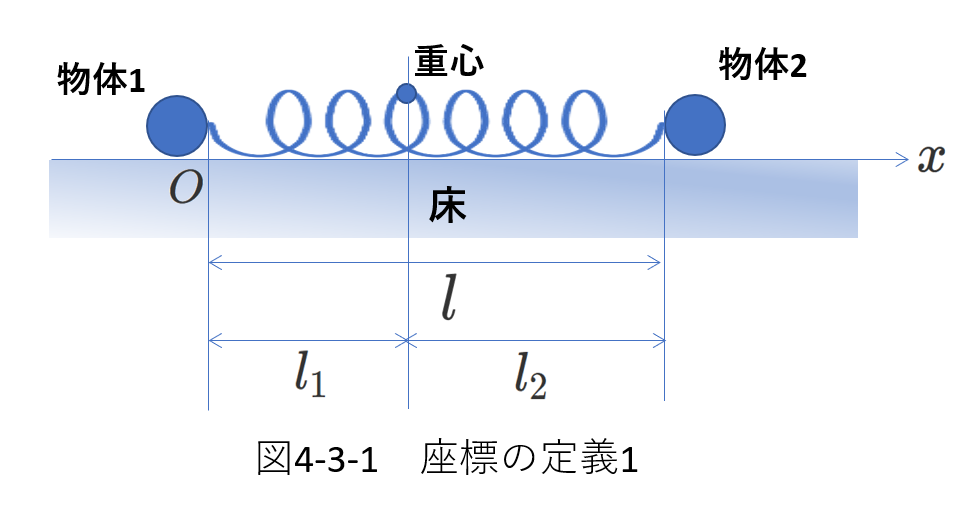
　ばねが自然長\(l\)のときの物体1の位置を原点として、右向き正の座標軸を考えます。（右図4-3-1を参照）
また、物体1と物体2の体積は十分小さいと考えます。

 

　すると重心の座標は、
\begin{equation} \frac{m_1\cdot 0+m_2l}{m_1+m_2}=\frac{m_2l}{m_1+m_2} \tag{4-10} \label{nitai4-10} \end{equation}
です。
　したがって、
\begin{eqnarray} l_1&=&\frac{m_2l}{m_1+m_2} \tag{4-11} \label{nitai4-11} \\
l_2&=&l-l_1=l-\frac{m_2l}{m_1+m_2}=\frac{m_1l}{m_1+m_2} \tag{4-12} \label{nitai4-12}
\end{eqnarray}

 

　これらを、(\ref{nitai4-07})、(\ref{nitai4-08})式 に代入すれば、
\begin{eqnarray} \omega_1&=&\sqrt{\frac{kl}{m_1l_1}}=\sqrt{\frac{k}{\frac{m_1m_2}{m_1+m_2}}} \tag{4-13} \label{nitai4-13} \\
\omega_2&=&\sqrt{\frac{kl}{m_2l_2}}=\sqrt{\frac{k}{\frac{m_1m_2}{m_1+m_2}}} \tag{4-14} \label{nitai4-14}
\end{eqnarray}

 

　「Ⅱ．二体問題を整理する」と同じように、換算質量\(\mu=\frac{m_1m_2}{m_1+m_2}\)を考えると、
\begin{equation} \omega_1=\omega_2=\sqrt{\frac{k}{\mu}} \tag{4-15} \label{nitai4-15} \end{equation}

 

 

 

 

 

 

[解2]

 

　物体1と物体2の運動方程式を立て、それを重心から観察した運動方程式に書き直します。
求めた単振動の運動方程式から、単振動の角振動数を求めます。

 

 

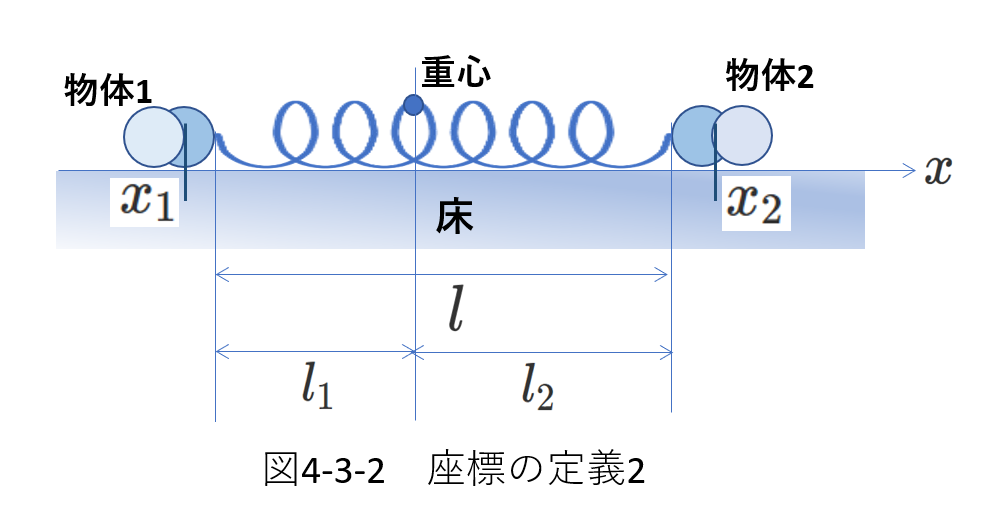
　右図4-3-2のように、右向き正の座標軸を考えます。
また、物体1と物体2の体積は十分小さいと考えます。

 

　物体1の座標を\(x_1\)、物体2の座標を\(x_2\)、ばねの自然長を\(l\)とします。
　床から観察した物体1と物体2の運動方程式は、
\begin{eqnarray} m_1a_1&=&k\left((x_2-x_1)-l\right) \tag{4-16} \label{nitai4-16} \\
m_2a_2&=&-k\left((x_2-x_1)-l\right) \tag{4-17} \label{nitai4-17}
\end{eqnarray}

 

また、物体1と物体2の重心の加速度を\(a_G\)、重心から見た物体1，物体2の相対加速度を\(a_{1G}\)、\(a_{2G}\)とすると、
\begin{eqnarray} a_1-a_G&=&a_{1G} \\
a_2-a_G&=&a_{2G} \\
この系では運動量保存則が成り立つこと&、&初期状態で系の運動量は0であることから、　\\
重心は全ての時刻で静止していますから&、&a_G=0です。 したがって、 \\
a_1&=&a_{1G} \\
a_2&=&a_{2G}
\end{eqnarray}

 

　このような場合、どのような形の式が求まれば良いかを予想しておくと、式を変形する方針が立てられます。
物体1の重心から見たときの運動方程式は、単振動の方程式ですから、次の形になるはずです。
\begin{equation} m_1a_{1G}=-[正の係数]\left([重心から見た物体1の座標]-[重心から見た振動の中心]\right) \tag{4-18} \label{nitai4-18} \end{equation}
重心の座標を\(x_G\)とすれば、
\begin{equation} x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2} \tag{4-19} \label{nitai4-19} \end{equation}

 

[重心から見た物体1の座標]は\((x_1-x_G)\)ですから、(\ref{nitai4-16})式中の\(x_2\)を消去する必要があることがわかります。
それには、(\ref{nitai4-19})式から\(x_2\)を求め、それを（\ref{nitai4-16}）式に代入します。
そうすると、右辺に\((x_1-x_G)\)が現れそうだと、予測を立てます。

 

　(\ref{nitai4-19})式から、\(x_2=\frac{m_1+m_2}{m_2}x_G-\frac{m_1}{m_2}x_1\)ですから、
\begin{eqnarray} m_1a_1&=&k\{(x_2-x_1)-l\} \tag{4-16} \\
m_1a_{1G}&=&k\left(\frac{m_1+m_2}{m_2}x_G-\frac{m_1}{m_2}x_1-x_1-l\right) \\
m_1a_{1G}&=&k\left(\frac{m_1+m_2}{m_2}x_G-\frac{m_1+m_2}{m_2}x_1-l\right) \\
m_1a_{1G}&=&-k\left(\frac{m_1+m_2}{m_2}(x_1-x_G)+l\right) \\
m_1a_{1G}&=&-\frac{k(m_1+m_2)}{m_2}\left(x_1-x_G+\frac{m_2l}{m_1+m_2}\right) \\
m_1a_{1G}&=&-\frac{k(m_1+m_2)}{m_2}\{\left(x_1-x_G\right)-\left(-\frac{m_2l}{m_1+m_2}\right)\} \tag{4-20} \label{nitai4-20} \\
\frac{m_1m_2}{m_1+m_2}a_{1G}&=&-k\{(x_1-x_G)-\left(-\frac{m_2l}{m_1+m_2}\right)\} \tag{4-21} \label{nitai4-21}
\end{eqnarray}

 

　(\ref{nitai4-20})式を見ると、重心から物体1を見たとき、ばね定数は\(k\frac{m_1+m_2}{m_2}\)となります。
その振動の中心は重心から見たとき、\(\frac{m_2l}{m_1+m_2}\)だけ重心から左に離れている点であることがわかります。

 

　(\ref{nitai4-21})式を解釈すると、ばね定数が\(k\)で、物体1の質量を換算質量とした単振動をするということがわかります。

 

 

　物体2について、同様の考察をします。

 

　　(\ref{nitai4-19})式から、\(x_1=\frac{m_1+m_2}{m_1}x_G-\frac{m_2}{m_1}x_2\)ですから、これを（\ref{nitai4-17}）式に代入して、
\begin{eqnarray} m_2a_2&=&-k\{(x_2-x_1)-l\} \tag{4-17} \\
m_2a_{2G}&=&-k\left(x_2-\frac{m_1+m_2}{m_1}x_G+\frac{m_2}{m_1}x_2-l\right) \\
m_2a_{2G}&=&-k\left(\frac{m_1+m_2}{m_1}x_2-\frac{m_1+m_2}{m_1}x_G-l\right) \\
m_2a_{2G}&=&-k\left(\frac{m_1+m_2}{m_1}(x_2-x_G)-l\right) \\
m_2a_{2G}&=&-\frac{k(m_1+m_2)}{m_1}\left(x_2-x_G+\frac{m_1l}{m_1+m_2}\right) \tag{4-22} \label{nitai4-22} \\
\frac{m_1m_2}{m_1+m_2}a_{2G}&=&-k\{(x_2-x_G)-\left(-\frac{m_1l}{m_1+m_2}\right)\} \tag{4-23} \label{nitai4-23}
\end{eqnarray}

 

　物体1の運動方程式（\ref{nitai4-20}）も、物体2の運動方程式（\ref{nitai4-22}）も運動が単振動であることを表していて、その角振動数はどちらも\(\sqrt{\frac{k}{\mu}}\)であることがわかります。
また、（\ref{nitai4-11}）（\ref{nitai4-12}）式を見れば、振動中心はばねが自然長のときの物体1、物体2の位置にあることがわかります。

 

 

 

 

 

 

２．ゴムひもでつながった二体の運動

 

 

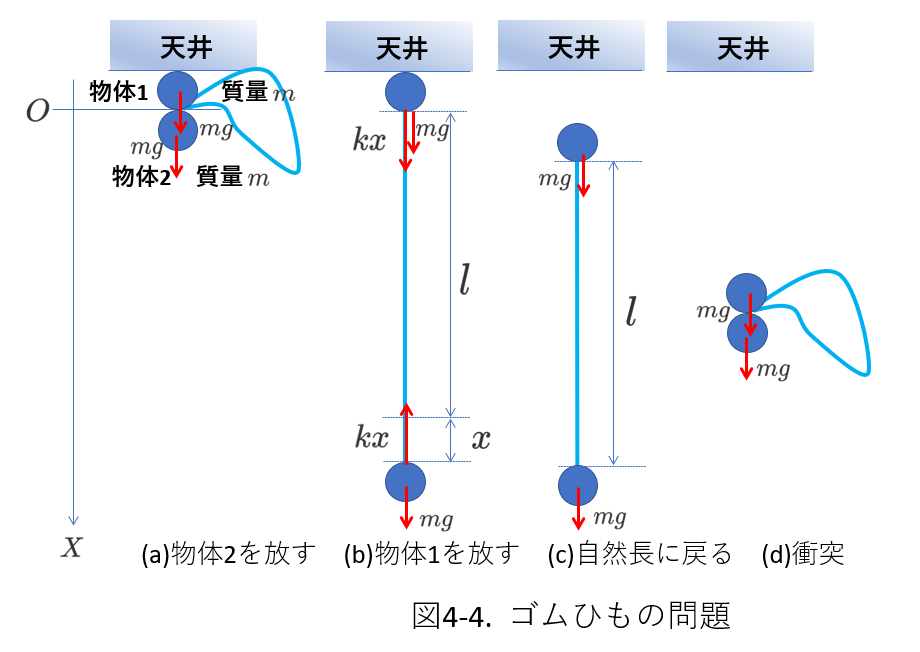
　次の例は京都大学の問題ですが、図4-4に示したように、ふたつの物体がゴム紐で結ばれています。

 

　ゴム紐を使った問題は時々出題されますが、次のような特徴を持っていると説明されるのがほとんどです。

 

１．ゴム紐が伸びているときには、ばねのようにはたらきます。
　　つまり、ばね定数を\(k\)、ゴム紐の伸びを\(x\)とすると、\(kx\)の弾性力がはたらきます。

 

２．ゴム紐がたわんでいる場合、ゴム紐に繋がるふたつの物体に何の力もはたらきません。
　　つまり、ふたつの物体の間隔がゴム紐の自然長以下の場合、ふたつの物体にはゴム紐からの力ははたらきません。

 

 

 

　今、図4-4に示したように、同じ質量\(m\)を持つふたつの物体がゴム紐で繋がれています。
物体1と物体2を天井に固定しておいて、物体2のみ静かに放します。（図4-4(a)）
物体2はそのまま下降し、ゴム紐が最大に伸びた瞬間に物体1を放します。(図4-4(b)）
ゴム紐は縮み始め、ある時点で自然長に戻ります。（図4-4(c)）
物体1と物体2の間隔はさらに縮まり、ふたつの物体は衝突をします。（図4-4(d)）

 

　物体1と物体2が衝突をしたときの位置、天井からの距離を求めます。

 

 

　物体1と物体2の運動をイメージしましょう。
　最初に、物体2の運動を考えます。

 

　運動を考えるには、物体1が受ける力を考えます。
放した直後には重力のみがはたらき、下向きに加速されます。

 

　ゴム紐が自然長からさらに伸びると、重力に加えて上向きの弾性力がはたらき、物体2の速度は小さくなり、ゴム紐が最大に伸びたところで速さは\(0\)になります。
このとき、物体1が放されます。

 

　物体1が放されたとき、物体1には重力と下向きの弾性力がはたらきます。
物体2には重力と上向きの弾性力がはたらきますから、物体1と2の距離は縮まり、自然長になります。

 

　間隔が自然長に戻ったら、ふたつの物体にはたらく力は重力のみになります。
そして、ふたつの物体は衝突します。

 

 

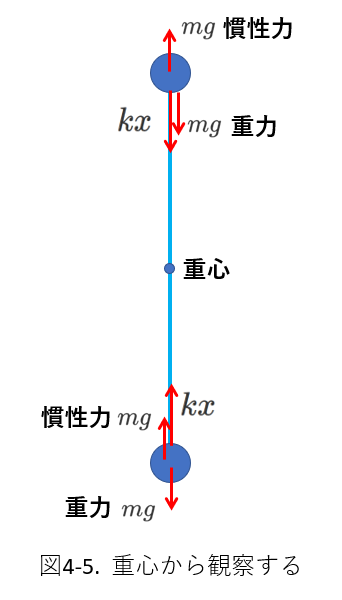
　では、これまでの説明を踏まえて、ふたつの物体の運動を重心から観察します。

 

 

　物体1を放したあと、ゴム紐の弾性力は、物体1と物体2とゴム紐からなる系を考えると、内力になり、外力は重力のみです。
したがって、重心は加速度\(g\)で等加速度運動をしていると推察されます。

 

　このとき、重心と一緒に運動する人から見ると、物体1にも物体2にも慣性力として、重力と同じ大きで逆向きの慣性力がはたらくので、重力と慣性力が相殺され、ゴム紐が自然長に戻るまでは、弾性力のみが働く、つまり重心が静止したまま、その両側で単振動をしているように見えます。

 

 

　自然長に戻ってからは、重心から観察すると、2つの物体には何の力もはたらかないので、物体1は下向きに等速直線運動、物体2は上向に等速直線運動をしているように見えるので、しばらくしてふたつの物体は衝突します。
このように、重心から運動を見るとわかりやすいです。

 

 

　さて、どう考えるかですが、ふたつの物体が衝突する場所は、重心のはずです。
その重心は、物体1を放してから衝突するまで、等加速度運動をしています。
だから、放してから衝突するまでの時間がわかれば、衝突位置もわかるはずです。

 

　運動はふたつに分かれます。

 

　ゴム紐が自然長に戻るまでと戻った後です。
　戻るまでは単振動をするので、単振動の周期がわかれば、時間を求められそうです。

 

　戻ってから衝突するまでの時間も、距離（すなわち、ゴム紐の自然長）と自然長になったときのふたつの物体の速さから求められそうです。

 

　方針が決まったので計算してみます。

 

 

 

　a．単振動の周期を求めます。

 

　静止している重心から各物体を見ると、ばね定数は\(2k\)ですから、角振動数\(\omega=\sqrt{\frac{2k}{m}}\)です。
したがって、周期\(T\)は、
\begin{equation} T=\frac{2\pi}{\omega}=2\pi \sqrt{\frac{m}{2k}} \tag{4-24} \label{nitai4-24} \end{equation}
となります。

 

　物体1を放したとき（時刻\(t=0\)）、ゴム紐は最大に伸びているので（また、放した直後の速度は\(0\)なので）このときが振動の下端です。

 

　振動の中心はどこでしょう。

 

 

　しかし、物体1が放され、重心から運動を観察している場合は、重力の効果が相殺されているので、自然長が振動の中心となります。

 

　ということは、自然長に戻るまでの時間\(t_1\)は、周期の\(\frac{1}{4}\)となります。
\begin{equation} t_1=\frac{T}{4}=\frac{\pi}{2}\sqrt{\frac{m}{2k}} \tag{4-25} \label{nitai4-25} \end{equation}

 

　b．自然長に戻った時の物体の速さ

 

　重心から観察したときにも、系の力学的エネルギーが保存されることを利用します。

 

　重心から見ると、重力ははたらいていないので、力学的エネルギーとして考えるのは、弾性エネルギーと運動エネルギーです。
物体1を放したときの、ゴム紐の弾性エネルギーは、このときのばねの伸びを\(x\)として、\(\frac{1}{2}kx^2\)です。
そして、自然長に戻った時の弾性エネルギーは\(0\)です。
自然長に戻ったときの物体2の速さを\(v\)とすれば、ふたつの物体は重心から見て対称的に単振動するので、物体2の速さも\(v\)です。
ただし、向きは逆です。
　力学的エネルギーの保存則は
\begin{eqnarray} \frac{1}{2}kx^2&=&\frac{1}{2}mv^2+\frac{1}{2}mv^2 \\
となり、
v^2=\frac{k}{2m}x^2 \\
v=\sqrt{\frac{k}{2m}}x \tag{4-26} \label{nitai4-26}
\end{eqnarray}

 

 

　\(v\)を求めるには、\(x\)を求める必要があります。
　\(x\)を求めるときには、外部から（静止している人から）見たときの力学的エネルギ保存則を用います。
すなわち、天井に固定していた物体2を放した直後の物体2の位置エネルギーが、物体2が最下端に達して（物体1を放す直前の）ゴム紐の弾性エネルギーに等しいと考えます。
位置エネルギーの基準を、物体1を放す直前の物体2の位置として、
\begin{eqnarray} mg(l+x)&=&\frac{1}{2}kx^2 \\
kx^2-2mgx-2mgl&=&0 \\
x&=&\frac{2mg+\sqrt{4m^2g^2-4\cdot k(-2mgl)}}{2k} \\
&=&\frac{mg+\sqrt{m^2g^2+2mgkl}}{k} \tag{4-27} \label{nitai4-27}
\end{eqnarray}
　\(x\gt0\)より、+を選択しています。

 

　さて、上の式は複雑なので、これが簡単になるように、問題では\(k=\frac{12mg}{l}\)であるとしています。
　これを代入すると、\(x=\frac{l}{2}\)が得られます。
ここでもこれらの値を採用することにします。

 

 

c．衝突する位置を求める

 

　以上より、
　自然長に戻ってから衝突するまでの時間\(t_2\)は、
\begin{eqnarray} t_2&=&\frac{l}{2v}=\frac{l}{2\sqrt{\frac{k}{2m}}x} \\
&=&\frac{l}{2\sqrt{\frac{k}{2m}}\frac{l}{2}}=\sqrt{\frac{ｌ}{6ｇ}} \tag{4-28} \label{nitai4-28} \\
これより、t_1+t_2&=&\frac{\pi}{2}\sqrt{\frac{m}{2k}}+\sqrt{\frac{l}{6g}}=(\frac{\pi}{4}+1)\sqrt{\frac{l}{6g}} \tag{4-29} \label{nitai4-29}
\end{eqnarray}

 

　そして、衝突する位置の天井からの距離は、
\(t=0\)での重心の位置は、天井から\(\frac{l+x}{2}\)の距離で、重心の初速度は\(0\)で加速度は\(g\)ですから、
求める距離\(L\)は、
\begin{equation} L=\frac{l+x}{2}+\frac{1}{2}g(t_1+t_2)^2 \tag{4-30} \label{nitai4-30} \end{equation}
を計算して、求められます。

 

 

 

 

 

 

 

関連ページ

作図

物理の問題を解く場合、図を描くことは必須と言えます。図を活用することで、考察が進み、その結果ミスを減らすことができます。図を活用する場合の注意点を説明しています。

運動方程式

物理の基本の運動方程式の立て方と用い方、合わせて、運動を制限する制約条件の考え方についても説明しています。

モーメントの考え方

力のモーメントについて、基本的注意事項のいくつかを説明しています。

運動量保存則を使う問題

運動量保存則は、力学でも最も重要な概念のひとつです。運動量が保存される場合と保存されない場合について説明し、例題を掲げました。

張力

糸につながれたおもりの運動では、糸の張力を考慮します。張力を考える場合のヒントを説明しています。

運動エネルギーと仕事の関係

運動エネルギー保存則は成立しない場合がありますが、仕事により運動エネルギーが変化するという関係は常に成立するため、問題を解くのに役立つ考え方です。

力学的エネルギー保存則を考える

力学的エネルギー保存則は物理で最も重要な概念のひとつです。力学的エネルギーが保存される場合と保存されない場合とを説明し、例題を掲げて解法について説明しています。

単振動

単振動に関する問題を解くときに必要な知識について説明をしています。

力積

力学は物理の基礎とも柱とも言えます。しっかり勉強して理解を深めましょう。

円運動

円運動を考えるには、向心力を用いて運動方程式を立てるか、遠心力で力のつりあいを考えます。円運動の問題は難しく感じますが、出題のパターンは多くありません。