力学的エネルギー保存則を考える

トップページ＞力学＞力学的エネルギー保存則を考える

Ⅰ．力学的エネルギー保存則を導く

　力学的エネルギー保存則は、「運動エネルギーと仕事の関係」から導かれます。
最初に重力がある場合について説明し、次にばねの弾性力がある場合について説明します。

（1）　重力がはたらく場合

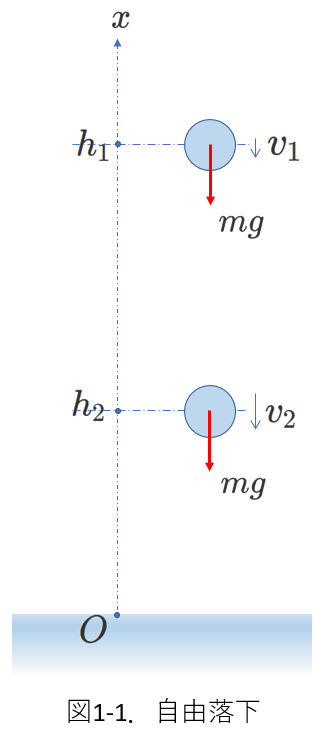
　図1-1は物体の自由落下を示しています。
　\(x\)軸の正の向きを鉛直上向きにとり、
\(x=h_1\)で速度\(v_1\)、\(x=h_2\)まで落下したとき、速度が\(v_2\)であったとします。

　このとき、重力\(mg\)が物体に対してした仕事は、\(mg\times (h_1-h_2)\)ですから、
「運動エネルギーと仕事の関係」から次の式が立てられます。
\begin{equation} \frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=mg(h_1-h_2) \tag{1-1} \end{equation}
　移行して整理すると、
\begin{equation} \frac{1}{2}mv_2^2+mgh_2=\frac{1}{2}mv_1^2+mgh_1 \tag{1-2} \end{equation}
　この式は、
［\(x=h_2\)での物体の力学的エネルギー]=[\(x=h_1\)での物体の力学的エネルギー]　 (1-3)
を表していて、力学的エネルギーが保存されることを意味しています。

　注）（1-2）式あるいは（1-3）式の形が力学的エネルギー保存の式の基本形で、
この形に書くことが、立式ミスを減らす有効な方法です。
いったん（1-2）式あるいは（1-3）式を立ててから、必要な式に変形するようにしましょう。

　（1-1）式は、[運動エネルギーの変化]=[重力による位置エネルギーの変化]として、
力学的エネルギー保存則を変形したものと言えますが、
どちらからどちらを引くか、添え字の1と2に注意が必要です。
（1-1）式は、[運動エネルギーの変化]は[重力による仕事]と考えて
立式するほうが、ミスが少ないはずで、その意味でこの式は、
「運動エネルギーと仕事の関係」を表していると、考えるべきでしょう。

　また、\(v_2\)を求めるという意識が強いと、次のような式を書くかもしれません。
\begin{equation} \frac{1}{2}mv_2^2=\frac{1}{2}mv_1^2+mg(h_1-h_2) \end{equation}
　この式は、\(x=h_2\)での運動エネルギーは、\(x=h_1\)での運動エネルギーに位置エネルギーの減少分を
加えたものに等しいという意味で、正しい式ですが、（1-2）式と比較すると、（たとえば）位置エネルギーの減少分を考えるのか、増加分を考えるのかで、符号のミスを起こしやすいようです。

　（1-2）式ならば、左辺に\(x=h_2\)での力学的エネルギーを書き出し、右辺に\(x=h_1\)での力学的エネルギーを書き出すというように、力学的エネルギー保存則を形式的に立てることができます。

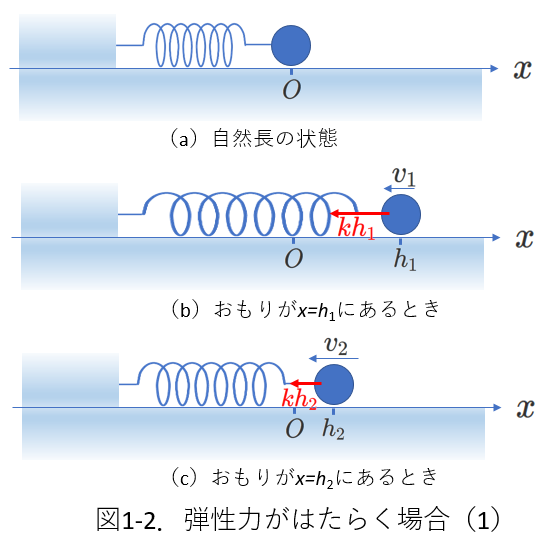
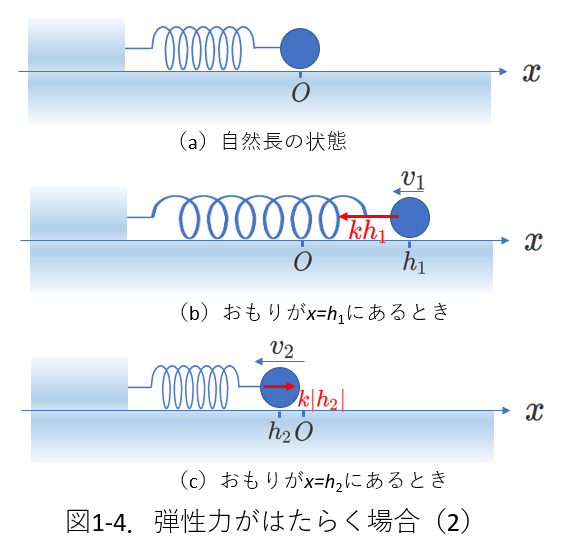
（2）　ばねの弾性力がはたらく場合

　図1-2に示すように、ばねのおもりが\(x\)軸の原点\(O\)にあるとき、
ばねは自然長です。（図（a））
　そして、ばね定数を\(k\)とします。

　今、おもりが\(x=h_1\)にあるとき、
おもりの速度の大きさが\(v_1\)、向きは左向き、（図（b））
時間が経過して、\(x=h_2\)に達したとき、おもりの速度の大きさは\(v_2\)、向きは左向きだったとします。（図（c））

　このときばねがおもりに対してした仕事は、
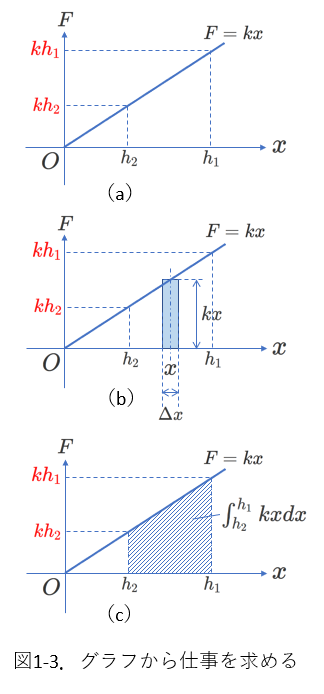
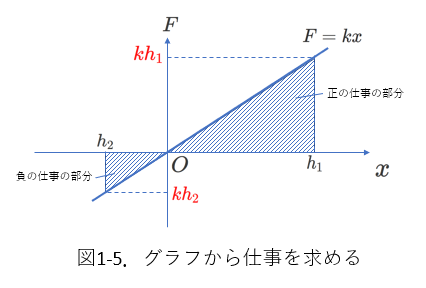
図1-3のようにグラフから求められます。
すなわち、ばねの弾性力\(F\)を表す式\(F=kx\)と\(x\)軸、
さらに、\(x=h_2\)と\(x=h_1\)で囲まれた面積(図（c）の斜線部分の面積）が
仕事を表します。

　ここで、おもりの進む向きと、ばねの弾性力の向きは一致しているので、
弾性力がおもりに対してする仕事は正です。

　以上より、
おもりに関して「運動エネルギーと仕事の関係」を式に表すと、
\begin{equation} \frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=\frac{1}{2}kh_1^2-\frac{1}{2}kh_2^2 \tag{1-4} \end{equation}
となります。

　移項して整理すると、
\begin{equation} \frac{1}{2}mv_2^2+\frac{1}{2}kh_2^2=\frac{1}{2}mv_1^2+\frac{1}{2}kh_1^2 \tag{1-5} \end{equation}
となります。　

　この式は、
[\(x=h_2\)のときの運動エネルギー+弾性エネルギー]
　　　　　　=[\(x=h_1\)のときの運動エネルギー+弾性エネルギー]　　　　（1-6）
であること、
すなわち、弾性エネルギーも含めた力学的エネルギー保存則を表しています。

　ばねの弾性エネルギーを含めた力学的エネルギー保存では、
図1-2で説明することが多いですが、図1-4についても考えてみます。

　図1-4では、おもりは、\(x=h_1\)の地点から原点\(O\)を通過し、
\(h_2\)まで移動しています。
　このため、図1-2では\(h_2>0\)であったのが、
図1-4では\(h_2<0\)となります。

　つまり、図1-4では、
\(x=h_1\)から原点\(O\)までは、弾性力がおもりにする仕事は正、
一方、原点\(O\)から\(x=h_2\)までは、
おもりの進む向きと、ばねの弾性力の向きが異なるため、
弾性力がおもりに対してする仕事は負となります。

以上のことと、図1-5を参考にしながら弾性力がおもりにする仕事を計算すると、
\begin{eqnarray} \frac{1}{2}kh_1^2+(-\frac{1}{2}k|h_2|^2） \\
= \frac{1}{2}kh_1^2-\frac{1}{2}kh_2^2
\end{eqnarray}
となります。

　したがって、「運動エネルギーと仕事の関係」を式に表すと、
\begin{equation} \frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=\frac{1}{2}kh_1^2-\frac{1}{2}kh_2^2 \tag{1-7} \end{equation}
となり、移項して並べ替えると、
　\begin{equation} \frac{1}{2}mv_2^2+\frac{1}{2}kh_2^2=\frac{1}{2}mv_1^2+\frac{1}{2}kh_1^2 \tag{1-8} \end{equation}
となります。

　これは、（1-5）（1-6）式と同じもので、力学的エネルギーが保存されることを意味しています。

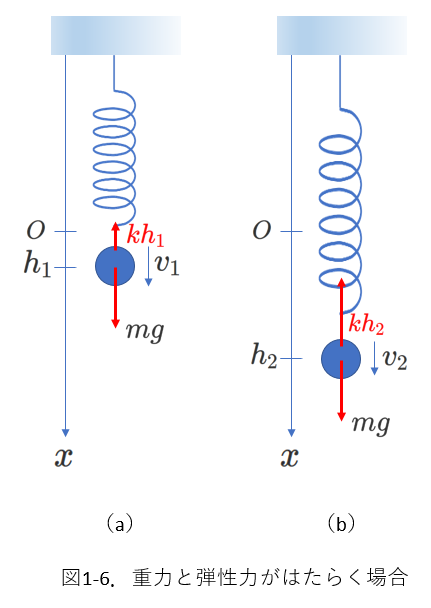
（3）　重力とばねの弾性力の両方がはたらく場合　

　ばねが天井から鉛直下向きに吊るされています。
ばねのばね定数を\(k\)、自然長のときにおもりは原点\(O\)の位置にあるものとします。

　今、おもりが\(x=h_1\)にあるとき、おもりの速度が\(v_1\)、
その後、\(x=h_2\)に達したときの速度を\(v_2\)とします。

　図1-6のように、おもりには重力とばねの弾性力がはたらいています。
重力は、\(x\)座標によらず一定であり、重力の向きとおもりが進む向きは一致しているので、
重力がおもりにする仕事は、\(mg(h_2-h_1)\)です。

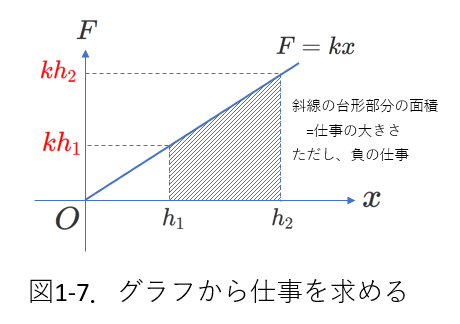
　一方、ばねの弾性力は伸縮量に応じて変化します。
したがって、グラフを使って考えます。
また、ばねの進む向きと弾性力の向きは逆向きですから、弾性力がおもりに対してする仕事は負です。

　図1-7に弾性力を求めるためのグラフを掲げました。

　ばねの弾性力がおもりに対してする仕事は、\(-\left(\frac{1}{2}kh_2^2-\frac{1}{2}kh_1^2 \right)\)　です。

　そして、[運動エネルギーの変化]=[重力がした仕事]+[弾性力がした仕事]という式を立てれば、
\begin{equation} \frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=mg(h_2-h_1)+\left(-\left(\frac{1}{2}kh_2^2-\frac{1}{2}kh_1^2 \right)\right)
　\tag{1-9} \end{equation}
　移項して整理すると、
\begin{equation} \frac{1}{2}mv_2^2-mgh_2+\frac{1}{2}kh_2^2=\frac{1}{2}mv_1^2-mgh_1+\frac{1}{2}kh_1^2 \tag{1-10}
\end{equation}
となります。
　重力による位置エネルギーの基準が原点\(O\)にあると考えると、
(1-10)式は、
[\(x=h_2\)における、運動エネルギー+重力による位置のエネルギー+弾性エネルギー]
　=[\(x=h_1\)における、運動エネルギー+重力による位置のエネルギー+弾性エネルギー]
すなわち、力学的エネルギー保存を示していることがわかります。

　(1-10)式をさらに変形して、ばねのつり合いの位置からの、ばねの伸縮を考えると
重力による位置エネルギーを考慮しなくて済むことを示します。

　つりあいの位置とは、ばねが振動せず静止している状態でのおもりの位置のことです。
このとき、重力とばねの弾性力はつりあうので、つりあいの位置の\(x\)座標を\(x_0\)として、
\begin{eqnarray} kx_0=mg \tag{1-11} \\
x_0=\frac{mg}{k} \tag{1-12}
\end{eqnarray}

また、このばねのおもりが座標\(x\)にあるときの加速度を\(\alpha\)として
おもりの運動方程式を求めると、
おもりにはたらく力は重力\(mg\)と弾性力\(kx\)ですから、下向きを加速度と力の正の向きとして、
\begin{eqnarray} m\alpha&=&mg-kx \\
&=&-k(x-\frac{mg}{k})　　　\tag{1-13}
\end{eqnarray}
となります。

　この式は単振動を表す式で、\(x=\frac{mg}{k}\)で加速度\(\alpha=0\)となることから、
振動の中心が\(x=\frac{mg}{k}\)にあることを示しています。
つまり、単振動の運動方程式からもつりあいの位置（=振動中心）を求めることができます。

　次に、（1-10）式の\(mg\)を、（1-11）式にしたがって\(kx_0\)に置き換えます。
そのあと、等式の両辺に\(\frac{1}{2}kx_0^2\)を加え、
等式を整理します。
\begin{eqnarray} \frac{1}{2}mv_2^2-mgh_2+\frac{1}{2}kh_2^2&=&\frac{1}{2}mv_1^2-mgh_1+\frac{1}{2}kh_1^2 \tag{1-10} \\
\frac{1}{2}mv_2^2-kx_0h_2+\frac{1}{2}kh_2^2&=&\frac{1}{2}mv_1^2-kx_0h_1+\frac{1}{2}kh_1^2 \\
\frac{1}{2}mv_2^2+\frac{1}{2}kx_0^2-kx_0h_2+\frac{1}{2}kh_2^2&=&\frac{1}{2}mv_1^2+\frac{1}{2}kx_0^2-kx_0h_1+\frac{1}{2}kh_1^2 \\
\frac{1}{2}mv_2^2+\frac{1}{2}k(x_0^2-2x_0h_2+h_2^2)&=&\frac{1}{2}mv_1^2+\frac{1}{2}k(x_0^2-2x_0h_1+h_1^2) \\
\frac{1}{2}mv_2^2+\frac{1}{2}k(h_2-x_0)^2&=&\frac{1}{2}mv_1^2+\frac{1}{2}k(h_1-x_0)^2 \tag{1-14}
\end{eqnarray}

　(1-14)式は、重力と弾性力がつりあう位置からの変位から弾性エネルギーを計算した場合には、
重力による位置エネルギーを考慮しなくても良いということを意味しています。
一方(1-10)式は、自然長からの変位から弾性エネルギーを計算しており、
このときには、重力による位置エネルギーの項が必要になります。

Ⅱ．力学的エネルギーが保存される場合

　力学的エネルギーが保存される場合を表に表します。
そのあと、それぞれの場合について、どんな状況があるのか具体的に検証します。

　以下に、力学的エネルギーが保存される場合を示します。

番号	系	条件	詳細
1-1	ひとつの物体（単独）	物体に加わる力がすべて保存力	保存力は、重力・万有引力・弾性力・静電気力 ※ 自然落下、衛星
1-2	ひとつの物体（単独）	物体に加わる非保存力が物体に対して仕事をしない	非保存力の向きが進む向きに垂直 ※ 坂道、鉛直面の円運動
2	２個以上の物体からなる系	２物体間にはたらく抗力や張力が、2個の物体に対してする仕事が相殺される	２物体は接触、あるいは、糸でつながれていて、一方にはたらく抗力・張力は他方にはたらくものと大きさが等しく向きが逆
3	２個の物体からなる系	弾性衝突（反発係数=1の場合）	運動量保存則が適用できる衝突、分離、一体化は、弾性衝突の場合を除いて、力学的エネルギーは保存されない
4	特別な場合	単振動とみなせる運動	水に浮いた浮きの単振動

（1）　1個の物体で保存される

1-1．　物体に加わる力がすべて保存力

　保存力とは、
　物体を移動させたとき、ある力のする仕事が途中の道筋によらないで決まる場合、
　その力を保存力と言います。

　保存力：重力、万有引力、ばねの弾性力、静電気力　（これらの力に対しては位置エネルギーを考えることができます）
　非保存力：摩擦力、垂直抗力、張力、空気抵抗　
（たどる道筋によって力が為す仕事が異なるため、位置エネルギーを考えることができません。）

　それでは、具体的な例を挙げます。

・1-1-1　重力：自由落下

　図1-1をもう一度右に掲げます。

　重力による位置エネルギーの基準を原点\(O\)にとると、
力学的エネルギー保存の式は次のように表されます。

\begin{equation} \frac{1}{2}mv_1^2+mgh_1= \frac{1}{2}mv_2^2+mgh_2 \tag{2-1} \end{equation}

　この式は、[\(x=h_1\)での力学的エネルギー]=[\(x=h_2\)での力学的エネルギー]　の形で、
最もよく使われるものです。
　力学的エネルギー保存の式を用いる場合は、最初にこの形の式を立て、それから必要な形に式変形するのが良いです。
何より、（2-1）式は形式的に書けるので、ミスが少なくなります。

　さて、次の表現の式も覚えておくと良いです。
　座標\(x\)での物体の速度を\(v\)として、
\begin{equation} \frac{1}{2}mv^2+mgx=一定　\tag{2-2} \end{equation}

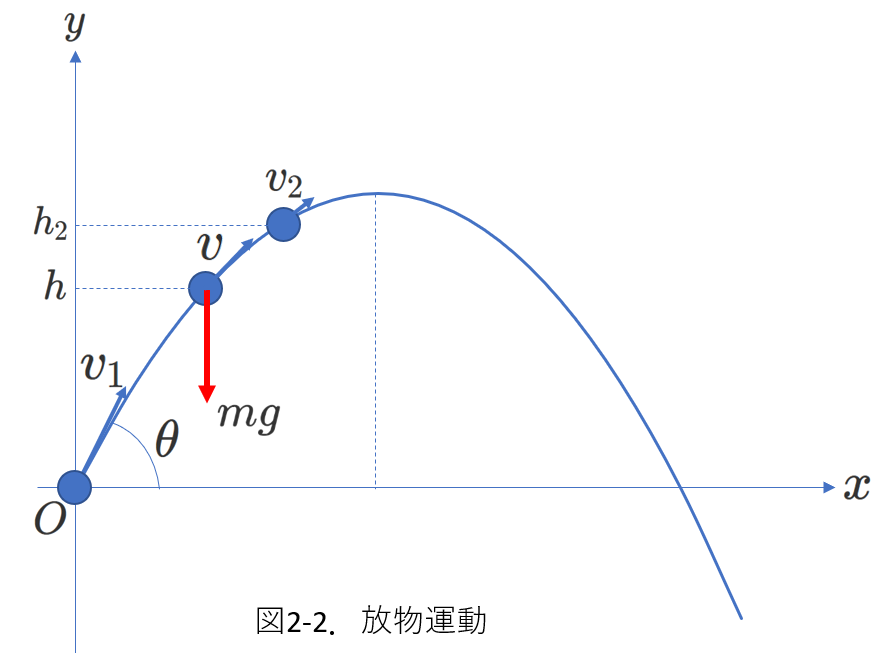
・1-1-2　重力：物体を投げた場合の放物運動

　次は物体を投げ上げた場合の運動です。

　右図のように、質量\(m\)の物体を水平方向との角度\(\theta\)で、
初速度\(v_1\)で投げ上げます。

　重力による位置エネルギーの基準を原点\(O\)とし、
高さが\(h_2\)のときの速度が\(v_2\)であるとすると、
力学的エネルギー保存の式は、
\begin{equation} \frac{1}{2}mv_1^2+mg\times 0=\frac{1}{2}mv_2^2+mgh_2 \tag{2-3} \end{equation}
　また、
\begin{equation} \frac{1}{2}mv^2+mgh=一定　\tag{2-4} \end{equation}
とも表現できます。

　さて、\(v_1、v_2\)の水平方向成分と鉛直方向成分をそれぞれ、\((v_{1x}、v_{1y})、(v_{2x}、v_{2y})\)とすると、
物体に対して水平方向にはたらく力はないので、\(v_{1x}=v_{2x}\)です。
（2-3）式より、
\begin{eqnarray} \frac{1}{2}mv_1^2+mg\times 0&=&\frac{1}{2}mv_2^2+mgh_2 \tag{2-3} \\
\frac{1}{2}m(v_{1x}^2+v_{1y}^2)+mg\times 0&=&\frac{1}{2}m(v_{2x}^2+v_{2y}^2)+mgh_2 \\
\frac{1}{2}mv_{1y}^2+mg\times 0&=&\frac{1}{2}mv_{2y}^2+mgh_2
\end{eqnarray}

　この例の場合、鉛直方向の速度の運動エネルギーと重力による位置エネルギーで力学的エネルギー保存が成り立ちました。
（これは一般的に言えることではありません。）
重力のはたらく方向が鉛直方向であり、重力が仕事をしたことで鉛直方向の速度が変化したと考えられます。

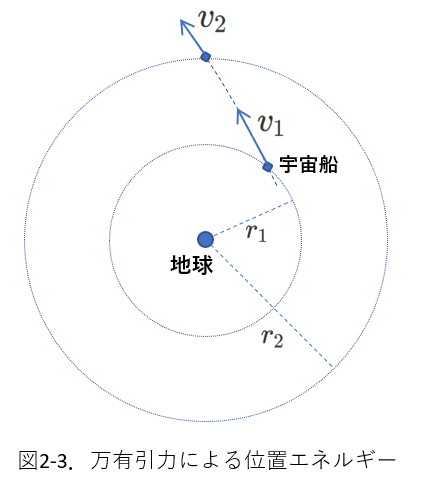
・1-1-3　万有引力：衛星の運動

　地球を離れた宇宙船が地球の重心から\(r_1\)の距離離れたところから、\(r_2\)離れたところに移動したところです。
宇宙船の質量は\(m\)、\(r_1\)のところでの宇宙船の速さは\(v_1\)、\(r_2\)のところでの速さは\(v_2\)です。
　地球の質量を\(M\)、万有引力定数を\(G\)として、
力学的エネルギー保存を表す式は、次のようになります。
\begin{equation} \frac{1}{2}mv_1^2-G\frac{Mm}{r_1}=\frac{1}{2}mv_2^2-G\frac{Mm}{r_2} \tag{2-4} \end{equation}
\(-G\frac{Mm}{r_1}\)、\(-G\frac{Mm}{r_2}\)は、万有引力による位置エネルギーです。
\(x \to \infty\)で位置エネルギー\(\to 0\)ですから、\(\infty\)が万有引力による位置エネルギーの基準です。

　宇宙船は、地球との万有引力にさからって、\(r_1\)の位置から\(r_2\)の位置に移動します。
（万有引力が宇宙船に対して負の仕事をするわけです。）
したがって、\(r_2\)での位置のエネルギーのほうが高く、宇宙船の運動エネルギーは減少していきます。

　宇宙船の運動エネルギーは、地球から離れるにつれて減少するので、
「宇宙船が到達できる地球からの距離」や「宇宙の端」までいけるかどうか」という問題が出題されることになります。

　この問題を解くには、力学的エネルギー保存則を使います。
　今、地球から\(r_1\)離れた位置で宇宙船の速度が\(v_1\)であるとき、
地球から離れられる距離を求めることにします。

　宇宙船が地球から最大離れたところでは、\(v_2=0\)となるはずですから、
この値を（2-4）式に代入して、\(r_2\)の最大値を求めることができます。
すなわち、
\begin{eqnarray} \frac{1}{2}mv_1^2-G\frac{Mm}{r_1}&=&\frac{1}{2}m\times 0^2-G\frac{Mm}{r_2} \\
G\frac{Mm}{r_2}&=&G\frac{Mm}{r_1}-\frac{1}{2}mv_1^2 \\
r_2&=&\frac{1}{\frac{1}{r_1}-\frac{v_1^2}{2GM}} \\
&=&\frac{2GMr_1}{2GM-v_1^2r_1} \tag{2-5}
\end{eqnarray}

　特別な場合として、\(r_2\to\infty\)の場合、つまり、宇宙船が無限遠に到達するための\(v_1\)は、
（2-5）式の分母が\(0\)として、\(v_1=\sqrt{\frac{2GM}{r_1}}\)、
この条件のとき、宇宙船は無限遠で速さがちょうど\(0\)になるわけですから、\(v_1\geqq \sqrt{\frac{2GM}{r_1}}\)が宇宙船が無限遠に到達できる条件になります。

　また、同じような考えですが、（2-4）式を変形して、
　\begin{equation} \frac{1}{2}mv_1^2-G\frac{Mm}{r_1}+G\frac{Mm}{r_2}=\frac{1}{2}mv_2^2\geqq 0 \tag{2-5'} \end{equation}
として、宇宙船が存在できる範囲を求めることができます。
　つまり、運動エネルギーが正である領域が、宇宙船の存在できる範囲で、（2-5'）式を\(r_2\)について解けば、その範囲を求めることができます。

　この考え方は非常に有用な方法です。
　・放物運動では、最高到達点を求めることができます。
　・宇宙船が到達できる点を求めることができます。
　・ばねの弾性力では、おもりの存在範囲（つまり、振動の端）を求めることができます。

・1-1-4　ばねの弾性力：ばねのおもりの運動

　水平面上に、片方の端を固定され他端に質量\(m\)のおもりがついたばねがあります。
　ばねが自然長のときのおもりの位置を\(x\)軸の原点\(O\)として、
おもりを引っ張って、\(x=x_0\)の位置までばねを伸ばしたあと、
静かにおもりを放します。

　おもりが\(x\)の位置にあるときの、速さを\(v\)として、力学的エネルギー保存則を表す式は、
ばね定数を\(k\)として、
\begin{eqnarray} &\frac{1}{2}mv^2&+\frac{1}{2}kx^2=\frac{1}{2}m\times 0^2+\frac{1}{2}kx_0^2 \tag{2-6} \\
または、 &\frac{1}{2}mv^2&+\frac{1}{2}kx^2=一定
\end{eqnarray}
です。

ここで、1-1-3と同じ考え方で、おもりの移動範囲を求めてみます。
（2-6）式を変形して、
\begin{eqnarray} \frac{1}{2}m\times 0^2+\frac{1}{2}kx_0^2-\frac{1}{2}kx^2&=&\frac{1}{2}mv^2\geqq0 \tag{2-7} \\
これより、-x_0\leqq x &\leqq& x_0
\end{eqnarray}
　この場合は、\(x=x_0\)で速度が\(0\)であることから、\(x=x_o\)は振動の端であることがわかります。
つりあいの位置から、振動中心は\(x=0\)であることが直ちにわかり、力学的エネルギー保存の式を立てるまでもなく、おもりの移動範囲がわかります。

　では、（2-6）式を次のように変形したら、\(v\)の範囲が求まるのでしょうか？
\begin{eqnarray} \frac{1}{2}m\times 0^2+\frac{1}{2}kx_0^2-\frac{1}{2}mv^2&=&\frac{1}{2}kx^2\geqq0 \tag{2-8} \\
これより、-\sqrt{\frac{k}{m}}x_0\leqq v &\leqq& \sqrt{\frac{k}{m}}x_0
\end{eqnarray}

　(2-8)式の等号が成り立つ場合を考えます。次のように式が変形できます。
\begin{eqnarray} \frac{1}{2}m\times 0^2+\frac{1}{2}kx_0^2&=&\frac{1}{2}mv^2 \\
\frac{1}{2}kx_0^2&=&\frac{1}{2}mv^2 \tag{2-9}
\end{eqnarray}
　（2-9）式は、[おもりが\(x=x_0\)にあるときの弾性エネルギー]=[弾性エネルギーが\(0\)となる\(x=0\)での運動エネルギー]
という式で、普通によく使われる式です。
したがって、（2-8）式の考え方は正しと言えます。

　さて、わざわざ(2-7)式を使って\(x\)の範囲を求めるのはおおげさですが、
次のような場合には、この力学的エネルギ―保存の式を使う方法は、効果的です。

　この例（右図2-4-2）では、\(x=x_0\)で初速\(v_0\)を与えています。
[図2-4-2（a）の力学的エネルギー]=[図2-4-2（b）の力学的エネルギー]という式を立てると、
\begin{eqnarray} \frac{1}{2}mv_0^2+\frac{1}{2}kx_0^2&=&\frac{1}{2}mv^2+\frac{1}{2}kx^2 \tag{2-10} \\
\frac{1}{2}mv_0^2+\frac{1}{2}kx_0^2-\frac{1}{2}kx^2&=&\frac{1}{2}mv^2 \geqq 0 \\
-\sqrt{\frac{m}{k}v_0^2+x_0^2} \leqq &x& \leqq \sqrt{\frac{m}{k}v_0^2+x_0^2}　\tag{2-11}
\end{eqnarray}

　検算の意味で、(2-11)式で\(v_o=0\)とすると、（2-7）式から求められた\(x\)の範囲と同じになり、
間違ってはいないようです。

　\(v\)の範囲を求めることもできて、次のように計算できます。
\begin{eqnarray} \frac{1}{2}mv_0^2+\frac{1}{2}kx_0^2&=&\frac{1}{2}mv^2+\frac{1}{2}kx^2 \tag{2-10'} \\
\frac{1}{2}mv_0^2+\frac{1}{2}kx_0^2-\frac{1}{2}kv^2&=&\frac{1}{2}mk^2 \geqq 0 \\
-\sqrt{v_0^2+\frac{k}{m}x_0^2} \leqq &v& \leqq \sqrt{v_0^2+\frac{k}{m}x_0^2}　\tag{2-11'}
\end{eqnarray}

　上の式は\(v\)の最大値\(v_{max}\)を示しています。
単振動の特徴から、[\(v_{max}\)]=[振幅]×[角周波数]であり、
(2-11)式から、[振幅]=\(\sqrt{\frac{m}{k}v_0^2+x_0^2}\)、[角周波数]=\(\sqrt{\frac{k}{m}}\)ですから、　
\begin{eqnarray} v_{max}&=&\sqrt{\frac{m}{k}v_0^2+x_0^2}\times \sqrt{\frac{k}{m}} \\
&=&\sqrt{v_0^2+\frac{k}{m}x_0^2}
\end{eqnarray}
となり、（2-11'）式と一致します。

・1-1-5　静電気力の場合

（a）点電荷の場合

　図2-5のように、固定された点電荷（電気量\(Q\)）の周りを、電気量\(q\)の物体が運動しています。

点電荷\(Q\)からの距離\(r_1\)のところで、電位\(V_1\)、物体の速度は\(v_1\)、
距離\(r_2\)のところで、電位\(V_2\)、物体の速度は\(v_2\)のとき、

力学的エネルギー保存則は、
\begin{equation} \frac{1}{2}mv_1^2+qV_1=\frac{1}{2}mv_2^2+qV_2 \tag{2-12} \end{equation}
と表されます。

　さて、点電荷のまわりの電位\(V_1、V_2\)は、クーロンの法則の比例定数を\(k\)として、
\begin{eqnarray} V_1=k\frac{Q}{r_1} \\
V_2=k\frac{Q}{r_2} \tag{2-13}
\end{eqnarray}

　これを（2-12）式の代入すると、
\begin{equation} \frac{1}{2}mv_1^2+k\frac{Qq}{r_1} =\frac{1}{2}mv_2^2+k\frac{Qq}{r_2} \tag{2-12} \end{equation}
ここで、\(k\frac{Qq}{r_1} 、k\frac{Qq}{r_2}\)は静電気力による位置エネルギーと呼ばれます。

　（2-12）式と、万有引力による位置エネルギーのところの（2-4）式と形が同じことを確認してください。
　（図2-3と図2-5も意識して似せて描いています。）
ただし、（2-4）式で質量\(m、M\)が正であるのに対して、
（2-12）式の\(q、Q\)は、正の場合も負の場合もあります。

　さて、（2-12）式で用いられた位置エネルギーの式および図2-5は、空間に固定された電荷が点電荷の場合でした。
電荷の分布が変わると、電場や電位や静電気力による位置エネルギーを表す式は異なります。

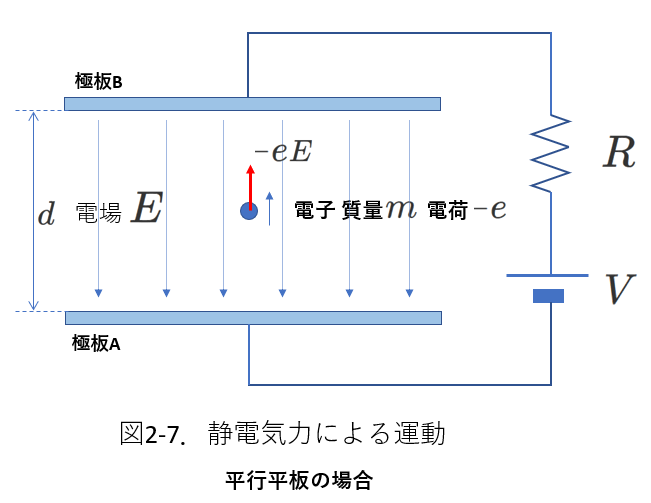
（b）平行平板の場合

　点電荷のほかには、高校物理では、
平行平板（つまりコンデンサなど）に蓄えられた電荷が作る一様な電場による電位と位置エネルギーを扱います。

　右図では、極板Aと極板Bとからなるコンデンサが、抵抗\(R\)を通して起電力\(V\)の電池につながっています。
今、極板Aに、質量\(m\)、電気量（電荷）\(-e\)の電子を置き、放したところ、電子は、電極Bに向かって移動しました。

　電極Bに達したときの電子の速さ\(v\)を求めます。
重力の寄与は小さいとして、無視してよいことにします。

　電位の基準を極板Aにおくと、極板Bの電位は\(V\)です。
これにより、極板Aでの電子の位置エネルギーは\(0\)、
極板Bでの電子の位置エネルギーは\(-eV\)です。

　したがって、力学的エネルギー保存則の式を立てると、
\begin{equation} \frac{1}{2}m\times 0^2+(-e\times 0)= \frac{1}{2}mv^2+(-eV) \tag{2-13} \end{equation}
これより、\(v=\sqrt{\frac{2eV}{m}}\)となります。

上の問題を運動方程式から考えてみます。

　右図（図2-7）のように、コンデンサーの極板間には、極板Bから極板Aに向かう一様な電場(強さ\(E\)）が存在します。
電場の向きを力と加速度の正の向きとすると、
電子は電場から\(-eE\)の力を受けます。

　電子の加速度を\(a\)として、運動方程式を立てると、
\begin{eqnarray} ma&=&-eE　\tag{2-14} \\
a&=&-\frac{eE}{m} \tag{2-15}
\end{eqnarray}

　極板間の距離は\(d\)で、電子は\(-d\) 変位して、速度が\(0\)から\(v\)まで変化したのですから、
\begin{eqnarray} v^2-0^2&=&2\left(-\frac{eE}{m}\right)(-d) \\
v&=&\sqrt{\frac{2eEd}{m}}
\end{eqnarray}

　ところで、電場\(E\)と電位\(V\)の間には、\(V=Ed\) の関係がありますから、
上で求めた\(v\)と、力学的エネルギー保存則から求めた\(v\)は一致しました。

1-2．物体に加わる非保存力が物体に対して仕事をしない

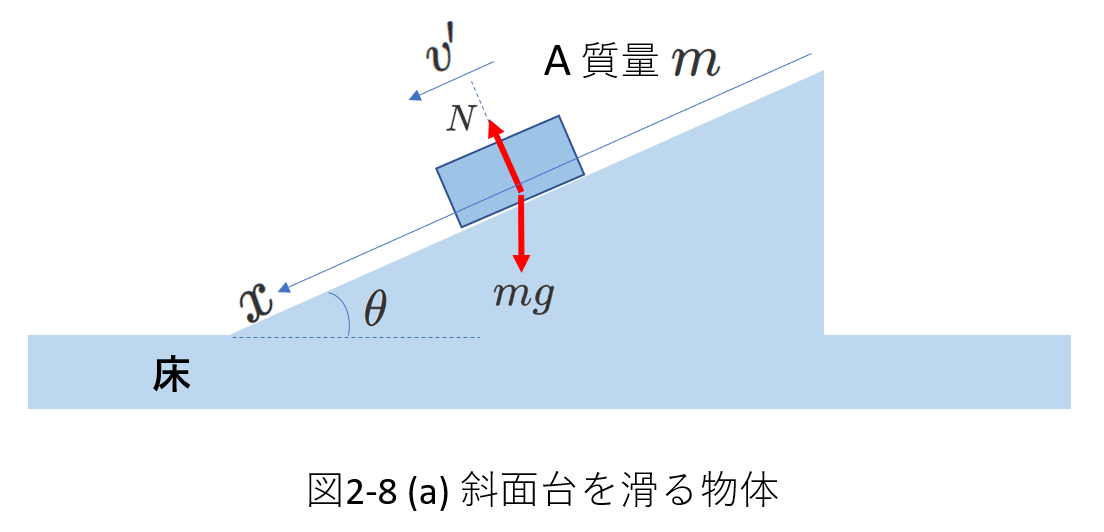
　例えば、右図（図2-8(a)）のように、斜面を滑る物体Aを考えます。

　Aには、重力\(mg\)のほかに斜面から垂直抗力\(N\)がはたらきます。
抗力は非保存力ですから、Aについて力学的エネルギー保存則は成り立たないように思いますが、
垂直抗力は、Aの進む方向に対して垂直の方向に働きます。

　つまり、垂直抗力はAに仕事をしていません。
このため、物体Aについて、力学的エネルギー保存則が成り立ちます。

　図2-8(b)を使って、物体Aについて力学的エネルギー保存則がなりたつことを導いてみましょう。

力学的エネルギー保存則が成立する場合と
しない場合があるのとは異なり、「運動エネルギーと仕事の関係」は常に成り立つので、これを使って導きます。

　図2-8(b)において、物体Aにはたらく斜面方向の力は、重力の斜面方向成分\(mg\sin{\theta}\)だけです。
ここで、斜面に沿って\(\frac{h}{sin{\theta}}\)だけ斜面を下がると、鉛直方向に\(h\)だけ変位することになります。
重力の斜面方向成分がした仕事は\(mg\sin{\theta} \times \frac{h}{sin{\theta}}\)です。

　この仕事により、物体Ａの斜面に沿った速さが\(v_1\)から\(v_2\)に変わります。
「運動エネルギーと仕事の関係」の式に表すと、

\begin{eqnarray} \frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=mg\sin{\theta} \times \frac{h}{sin{\theta}} \tag{2-16} \\
\frac{1}{2}mv_2^2=\frac{1}{2}mv_1^2+mgh \tag{2-17}
\end{eqnarray}
　(2-17)式は、Aの速さが\(v_2\)であるときのAの位置を重力による位置エネルギーの基準として
表した、物体Aについての力学的エネルギー保存の式と同じです。

　また、(2-17）式には斜面の角度\(\theta\)が含まれていないことに注意してください。

　右の図2-8(c)に、異なる角度を持つ4つの斜面台を滑る物体Aの運動を一つの図に表しました。

　\(y=h\)で静止させていた物体Aを斜面に沿って滑らせます。
Aが\(y=0\)に達したときの速さはいずれも同じ（\(v_2\)）です。
斜面の角度によって、Aが進む向きが異なることにも注意しましょう。

　問題によっては、図2-8(a)の斜面台と床が切り離されていて、斜面台が床に対して自由に動くという場合があります。
このとき、Aの力学的エネルギーは保存されるのでしょうか。

　これを図2-8（ｄ）に示します。図で斜面台が床との摩擦なしで動くことがわかりやすいように、斜面台には車輪がついています。
Aは斜面に沿って滑り降りますが、このとき斜面台は図の右向きに進みます。
　このため、床から見たとき、Ａは斜面と床の角度よりも大きい角\(\theta'\)で進みます。
このため、Ａが受ける垂直抗力の向きとＡの移動の向きは垂直からずれることになります。
つまり、垂直抗力はＡに対して仕事をすることになります。
　したがって、Ａの力学的エネルギーは保存されません。
次の（2）では、Ａ単独では力学的エネルギーは保存されませんが、
[Ａと斜面台の力学的エネルギーの和]は保存されることを説明しているので、参考にしてください。

　物体にはたらく非保存力が物体に対して仕事をしないので力学的エネルギー保存則が成り立つ例はほかにもあります。

　そのひとつは、円運動です。　
　図2-9では、小球Aが円筒形状の内面に沿って運動します。
図は断面を示していて、小球Aの運動はこの断面図内で行われるとします。

　小球は非保存力である垂直抗力\(N\)と、
保存力である重力\(mg\)を受けます。
ここで、\(N-mg\cos\theta\)が円運動の向心力に相当します。

　向心力は小球Aの運動の向きに垂直ですから、
\(N\)は小球に対して仕事をしません。
つまり、\(N\)によって小球Aの力学的エネルギーが
変化することはないので、小球Aに対して、
次の力学的エネルギー保存則が成り立ちます。
\begin{equation} \frac{1}{2}mv^2+mgr(1-\cos\theta)=一定 \tag{2-18} \end{equation}
　ここで、重力の位置エネルギーの基準を円筒状内面の最下端としています。

ちなみに、小球は円運動をしているので、次の円運動の運動方程式も成り立ちます。
\begin{equation} \frac{mv^2}{r}=N-mg\cos\theta \tag{2-19} \end{equation}
図2-9の設定で問題を解く場合には、(2-18)式と（2-19）式を2つとも用いることが多いです。
（2-18）式から\(v\)が\(\theta\)の関数として求められます。
これを（2-19）式に代入すると、垂直抗力\(N\)が\(\theta\)の関数として求められます。
鉛直面内の円運動では\(\theta\)によって速さは変わります。
この点が、水平面内の等速円運動と異なるところです。

　図2-9においても、内側が円筒の部分と床が切り離されていて、円筒部分が床に対して自由に動くという場合があります。
図2-8(d)の場合と同じく、この場合にも、A単独では力学的エネルギーは保存されません。

　図2-10の、糸でつるしたおもりが円運動する場合にも、図2-9と同様に考えることができます。

　図2-10では、物体Aにはたらくのは、張力\(T\)と重力\(mg\)です。
このうち、張力は非保存力です。
しかし、張力\(T\)は、物体Aが進む方向に垂直な向きにはたらくので、\(T\)は物体Aに対して仕事をしません。
したがって、この状況では、物体Aについて力学的エネルギー保存則が成り立ちます。

　今、糸がぴんと張った状態で(a）の位置に持ち上げ静かに放します。
糸と鉛直方向がなす角度が\(\theta\)になったときを(b)の位置として、
[(a)での力学的エネルギー]＝[(b)での力学的エネルギー]の形に力学的エネルギー保存則を表します。
ここで、(b)での物体Aの速さを\(v\)とし、重力による位置エネルギーの基準を、糸が鉛直の方向に一致したときの物体Aの位置とします。
物体は大きさがないものとして扱います。
\begin{equation} \frac{1}{2}m\times 0^2+mgr=\frac{1}{2}mv^2+mgr(1-\cos\theta) \tag{2-20} \end{equation}

円運動の運動方程式も(2-19)式と同様にして書けます。
\begin{equation} \frac{mv^2}{r}=T-mg\cos\theta \tag{2-19} \end{equation}

（2）　2個の物体からなる系で保存される

2-1. ふたつの物体が糸で結ばれた系

　1個の物体単独では力学的エネルギー保存則は成り立たないが、その物体に接触しているもうひとつの物体との力学的エネルギーの和を考えると、力学的エネルギー保存則が成立する場合があります。
　その一例が図2-11です。

　２つのおもりを糸でつなぎ、それを天井に固定した滑車に通しました。
おもりAの質量は\(m_1\)、おもりBの質量は\(m_2\)で、\(m_2\gt m1\)の関係があります。

今(a)の状態で静止させていたふたつのおもりを静かに離します。
すると、おもりAが上昇、Bが下降します。
(b)のそれぞれのおもりが\(h\)だけ移動した場合を考えます。
(b)の状態では、おもりAとおもりBの速さは同じです。これを、\(v\)とおきます。

　(b)におもりにはたらく力を示しましたが、それぞれのおもりにはたらく力は、糸の張力と重力です。
張力は非保存力で、1-2章で示した例と異なり、張力はおもりAに対しても、おもりBに対しても仕事をします。
したがって、A単独では力学的エネルギーは保存されません。
\begin{equation} 　\frac{1}{2}m_1\times0^2+m_1g\times0 \neq \frac{1}{2}m_1v^2+m_1gh \end{equation}
同じように、B単独では力学的エネルギーは保存されません。
\begin{equation} 　\frac{1}{2}m_2\times 0^2+m_2g\times0\neq \frac{1}{2}m_2v^2-m_2gh \end{equation}

　しかし、おもりAとおもりBの力学的エネルギーの和は保存されます。
つまり、[(a)の状態の｛Aの力学的エネルギー+Bの力学的エネルギー｝]=[(b)の状態の｛Aの力学的エネルギー+Bの力学的エネルギー｝]
で、式に表せば、
\begin{equation} \frac{1}{2}m_1\times0^2+m_1g\times0+\frac{1}{2}m_2\times0^2+m_2g\times0= \frac{1}{2}m_1v^2+m_1gh+\frac{1}{2}m_2v^2-m_2gh \tag{2-20} \end{equation}
が、成立します。
ここで、重力による位置エネルギーの基準を、それぞれのおもりに対して(a)の状態の位置としています。
　これを\(v\)について解けば、
\begin{eqnarray} \frac{1}{2}m_1v^2+\frac{1}{2}m_2v^2&=&m_2gh-m_1gh \\
v&=&\sqrt{\frac{2gh\left(m_2-m_1\right)}{m_1+m_2}}
\end{eqnarray}
となります。

　では、（2-20）式を導いてみます。
常に成り立つ「運動エネルギーと仕事の関係」を用います。

　おもりAに対して張力は\(Th\)の仕事をします。重力は、（おもりの進む向きと重力の向きが逆であることに注意して）\(-m_1gh\)の仕事をします。
これらの仕事により、Aの運動エネルギーは、\(0\)から\(\frac{1}{2}m_1v^2\)に変化します。したがって、
\begin{equation} \frac{1}{2}m_1v^2-0=Th-m_1gh \tag{2-21} \end{equation}
おもりBについても同様に考えて、
\begin{equation} \frac{1}{2}m_2v^2-0=-Th+m_2gh \tag{2-22} \end{equation}
となります。
(2-21)式と（2-22）式の各辺どうしを足して、
\begin{equation} \frac{1}{2}m_1v^2+\frac{1}{2}m_2v^2=-m_1gh+m_2gh \tag{2-23} \end{equation}
この式は（2-10）式と同じです。

　ポイントは
ＡとＢにはたらく張力の大きさは等しく、ＡとＢは同じ距離を進むので、
張力がＡとBにする仕事の大きさは等しいです。
　そして、糸の張力はAに対して正の仕事を、Bに対して負の仕事をするので、
和をとった場合、張力がする仕事は相殺されます。

さて、運動方程式を使っても\(v\)を求めることができます。
おもりA,Bの加速度はどちらも同じですから、これを\(a\)とします。
加速度と力の正の向きをA,Bが進む方向とします。
すると運動方程式は、
\begin{eqnarray} Aについて&:&m_1a=T-m_1g \\
Bについて&:&m_2 a=m_2g-T \\
ふたつの式のそれぞれの辺を足して&、& \\
(m_1+m_2)a&=&(m_2-m_1)g \\
a&=&\frac{m_2-m_1}{m_1+m_2}g \\
h移動して、速さが0からvに変わるので、\\
v^2-0^2&=&2ah \\
v&=&\sqrt{2ah} =\sqrt{\frac{2gh(m_2-m_1)}{m_1+m_2}}
\end{eqnarray}

　類似例に、図2-12があります。
　これは、図2-11とほぼ同じ状態です。
違いは、物体Aにはたらく重力がAに対して仕事をしないことです。
図2-12でも、物体Aと物体Bの力学的エネルギーの和が保存されます。

　ただし、問題によっては、物体Aと台の間に摩擦があるという場合があります。
すると、物体Aと物体Bの力学的エネルギーの和を考えても、保存されません。
摩擦力は、物体Aに対して負の仕事をします。
したがって、その仕事の分だけ、Aの力学的エネルギーが減少、
したがって、物体Aと物体Bの力学的エネルギーは減少します。

　上のことは、「運動エネルギーと仕事の関係」から考察できます。

　これまでの2例は、ふたつの物体が糸でつながれ、ふたつの物体は同じ距離進みます。
次に、ふたつの物体が垂直抗力を及ぼしあう、さらに複雑な系の例を挙げます。

2-2. 自由に動く斜面台とその上の物体からなる系

　右の図2-12(a)で、斜面台Bは床から切り離され、床と斜面台の間に摩擦はなく、自由に動くことができます。
図では、摩擦がないことを、斜面台に取り付けた車輪で表しています。
斜面台Bの上には、質量\(m\)の物体Aが置かれています。

　今、AとBを固定しておいて、それから、固定を外します。
すると、Aは斜面に沿って下向きに滑ります。
このときBは、Aから垂直抗力を受けて右方向に動きます。

　これらの動きを図に表したのが、図2-12(b)です。

床から見たとき、Aは赤色の一点鎖線のように動きます。
水平方向との角度を\(\theta'\)と表すと、\(\theta'>\theta\)です。
（\(\theta\)は、斜面の水平方向との角度です。）

　\(\theta'\)がわかっていないこと、
斜面台Bは水平方向に動き、鉛直方向には動かないことから、
水平方向を\(x\)軸、鉛直方向を\(y\) 軸とします。

　これから検証することは、
「物体Aと斜面台Bの力学的エネルギーの和が保存される」ことです。
物体Aと斜面台Bにはたらく力は、図2-12(a)に示すように、重力と垂直抗力です。
重力は保存力です。
　また、垂直抗力のうち斜面台と床が及ぼし合う垂直抗力\(N'\)は斜面台に対して仕事をしません。
つまり、AとBの力学的エネルギーの和を変えることはありません。

　したがって、AとBの間にはたらく垂直抗力\(N\)についてのみ、詳しく検討すればよいことになります。
以下で、垂直抗力\(N\)がAとBに対してする仕事の和が\(0\)であることを示します。

　図2-12(f)に、Aが斜面台Bから受ける垂直抗力\(N\)と、
斜面台BがAから受ける垂直抗力\(N\)のｘ成分とｙ成分を示します。

　今、Aがｙ方向下向きに\(y(\gt 0)\)の距離移動したとき、
Aがｘ方向左向きに\(x(\gt0)\)、Bがｘ方向右向きに\(X(\gt0)\)の距離移動したとします。
斜面台Bはｙ方向には動かないので、斜面台が受ける抗力のy成分は斜面台に対して仕事をしません。したがって、この項を考慮する必要はありません。

　さて、以上のように考えると、
Aが垂直抗力からされる仕事は、垂直抗力のｘ成分から、\(N\sin\theta\times x\)
　　　　　　　　　　　　　　垂直抗力のｙ成分から、\(-N\cos\theta\times y\) です。（Aの移動の向きと力の向きが逆です）
Bが垂直抗力のｘ成分からされる仕事は、\(N\sin\theta\times X\)
　　垂直抗力のｙ成分からされる仕事は、\(0\)です。　　
　つまり、\(N\sin\theta\times x+(-N\cos\theta\times y)+N\sin\theta\times X=0\)　を証明すればよいことがわかります。

　物体Aは角度\(\theta\)の斜面に沿って動くため、\(yとxとX\)の間には関係があります。
図2-12(g)の上の図は初期状態です。
ある時間経過した状態が下の図ですが、初期状態と重ねて示してあります。
黄色い点に注目してください。
この黄色い点が初期状態からどのように動いたかを考えるとわかりやすいです。

　図を参照すれば、
\begin{equation} \tan\theta=\frac{y}{x+X} \tag{2-24} \end{equation}
この式に、\(\tan\theta=\frac{\sin\theta}{\cos\theta}\)を適用し、両辺に\(N\)を掛けると、
\begin{eqnarray} \frac{\sin\theta}{\cos\theta}&=&\frac{y}{x+X} \tag{2-24} \\
(x+X)\sin\theta&=&y\cos\theta \\
Nx\sin\theta+NX\sin\theta&=&Ny\cos\theta \\
\end{eqnarray}

　この式は、上の証明すべき式と同値ですから、
「Aと斜面台Bの力学的エネルギーの和が保存される」ことが証明されました。

(3) 2個の物体が弾性衝突をする場合

　衝突の直前直後で運動量は保存されます。
しかし、力学的エネルギーはほとんどの場合、保存されません。
衝突のうち、弾性衝突の場合のみ。衝突の直前と直後で力学的エネルギーが保存されます。　

　最初に、衝突・一体化・分離のそれぞれの状態で力学的エネルギーと運動量が保存されるかどうかをまとめます。
次の表で、保存される場合を〇で、保存されない場合を×で示します。

項目	補足	力学的エネルギー	運動量
弾性衝突	反発係数（はね返り係数）=1の場合	〇	〇
弾性衝突以外の衝突	\(0\leqq反発係数（はね返り係数）\lt 1\)	×	〇
一体化	衝突の特別な場合で、反発係数（はね返り係数）=0	×	〇
分離	一体化していたものが複数の部分に分かれる	×	〇

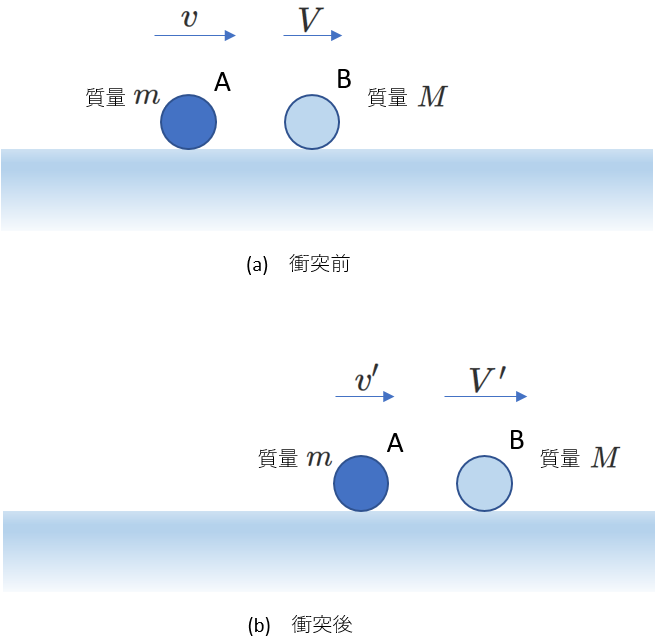
運動量保存：ふたつの物体の衝突

　最初に反発係数(はね返り係数）について復習します。
右図のようにふたつの物体A,Bの衝突を考えます。
このとき、反発係数\(e\)は次のように表されます。
\begin{equation} e=-\frac{V'-v'}{V-v} \tag{2-25} \end{equation}
　この式は、
\begin{equation} e=-\frac{衝突後の相対速度}{衝突前の相対速度} \tag{2-25} \end{equation}
と理解できます。
　相対速度の計算は、分母と分子で同じであれば、どちらからどちらを引いても良いです。
これより、弾性衝突（\(e=1\)）では、衝突直前と直後の相対速度の大きさは等しく、向きが逆であることがわかります。
（落としたボールが床で弾んで、もとの高さまで戻るというイメージです。）

　一体化は、離れていたふたつの物体が衝突により、くっついてしまうことです。
したがって、一体化後のふたつの物体の速度は同じですから、相対速度は\(0\)、
つまり、反発係数は\(0\)になります。

　なお、弾性衝突の場合に力学的エネルギーが保存されることは、「運動量保存則を使う問題」の章のⅨに示されています。
また、表に掲げた範囲では、ほとんどの場合、運動量は保存されても、力学的エネルギーが保存されないことがわかります。　
運動量と力学的エネルギーの違いを確認してください。
運動量はベクトル量（向きがある）であり、力学的エネルギーはスカラー量（向きはない）であることにも注意しましょう。

(4) 特別な場合
　力学的エネルギーが保存されるとみなせる場合があります。
次の水に浮いた浮きの単振動を考えてみます。
　

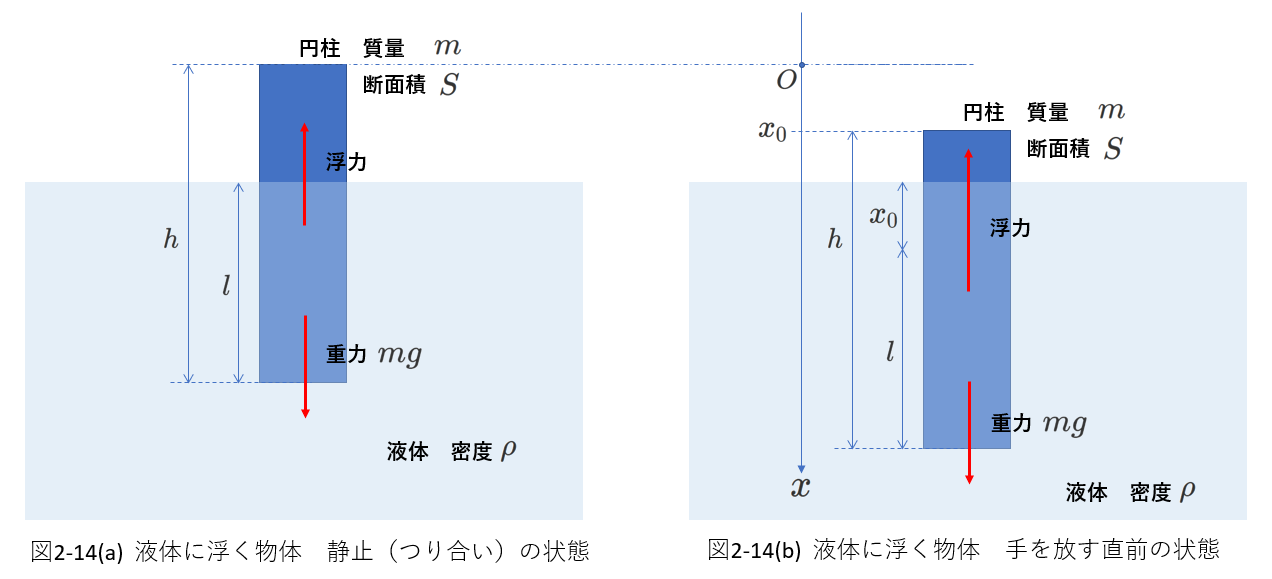
　図2-14(a)は、円柱形状の浮きが液体に浮いて静止している状態を示しています。
浮きの質量は\(m\)、断面積は\(S\)、長さは\(h\)で、重心は図で下側に寄っているものとします。
液体の密度は\(\rho\)です。
　(a)の状態で浮力の大きさは、\(lS\rho g\)です。

浮力の大きさは物体が押しのけた液体の重さに等しい、ということなので、
物体が押しのけた液体の体積は、\(lS\)、
その質量は、\(lS\rho\)、
これにはたらく重力の大きさは、\(lS\rho g\)、ですから、浮力は\(lS\rho g\)、です。

この力が、静止状態では、重力とつりあっているので、
\begin{eqnarray} mg&=&lS\rho g \\
l&=&\frac{m}{S\rho}　
\end{eqnarray}

　次に、図2-14(b)のように、浮きを距離\(x_0\)だけ液体に押し込め、静止させます。
\(x\)軸を鉛直方向に、\(x\)軸の正の向きを下向きとします。
そして、浮きがつり合いの状態にあるときの、上端の位置を\(x\)軸の原点とし、浮きの位置を浮きの上端の座標で表すことにします。

　固定を外し、円柱がつり合いの位置に戻ったときの、浮きの速さを求めてみます。

浮きが運動をして、\(x\)座標が\(x\)のときの加速度を\(a\)として運動方程式を立てると、次のようになります。
\begin{eqnarray} ma&=&mg-(l+x)S\rho g \\
&=&mg-lS\rho g-xS\rho g \\
&=&-S\rho gx \tag{2-26}
\end{eqnarray}

　（2-26）式は、単振動を表す式ですから、浮きが単振動をすることがわかります。
ばね定数を\(k\)とすれば\(k=S\rho g\)で、振動中心は\(x=0\)の位置です。
さて、単振動であることがわかったので、単振動のエネルギーが保存されると考えても良いことになります。
座標が\(x\)のときの速さを\(v\)とすると、単振動のエネルギー保存を表す式は、
\begin{eqnarray} 　\frac{1}{2}mv^2+\frac{1}{2}kx^2=一定　\\
\frac{1}{2}mv^2+\frac{1}{2}S\rho gx^2=一定
\end{eqnarray}

　この単振動のエネルギー保存の式を利用して、浮きが原点に戻った時の速さを求めます。
浮きは(b)の状態（\(x=x_0\)のとき）、円柱の速さは\(0\)であることを考えれば、
\begin{eqnarray} 　\frac{1}{2}m\times 0^2+\frac{1}{2}S\rho gx_0^2&=&\frac{1}{2}mv^2+\frac{1}{2}S\rho g\times 0^2　\\
\frac{1}{2}S\rho gx_0^2&=&\frac{1}{2}mv^2 \\
v=\sqrt{\frac{S\rho g}{m}}x_0
\end{eqnarray}

Ⅲ．力学的エネルギーが保存されない場合

　　力学的エネルギーが保存されない場合は、前の章の「Ⅱ．力学的エネルギーが保存される場合」から推測できます。
着目している物体や複数の物体からなる系に対して、非保存力が正味の仕事をする場合には、力学的エネルギーは保存されません。

（1）　弾性衝突を除く衝突・一体化・分離

　弾性衝突を除く衝突では、力学的エネルギーは保存されません。
別々に運動していたふたつの物体が衝突により一体となって運動するようになる「一体化」は、衝突の特別な場合（反発係数が\(0\)）で、この場合も、力学的エネルギーは保存されません。
　また、一体化の逆、運動していたひとつの物体が、複数の部分に分かれる「分離」でも、力学的エネルギーは保存されません。

（2）　ふたつの物体の間で摩擦力がはたらく場合

　摩擦力がはたらく場合は、力学的エネルギーが保存されません。

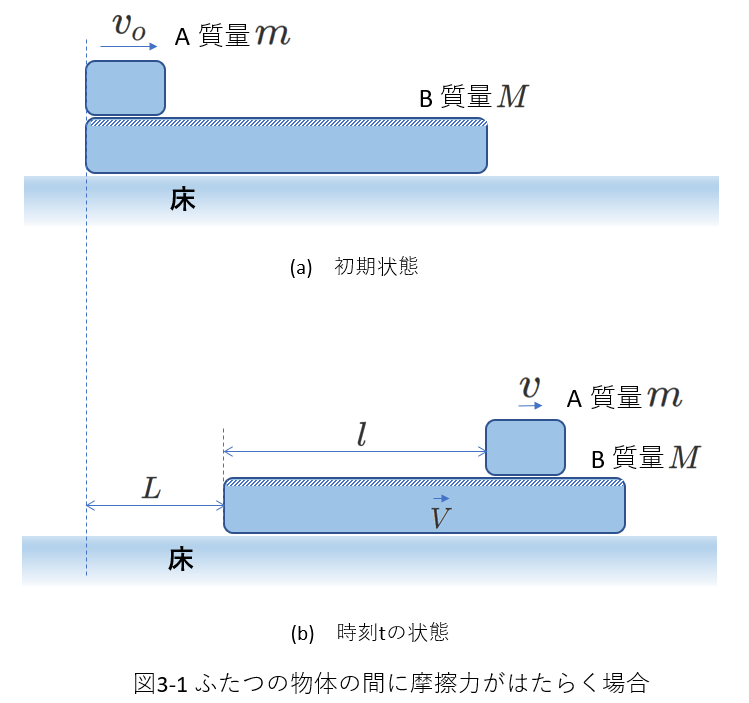
　右の図3-1の例を考えてみます。
床の上に質量\(M\)の物体Bと、Bの上に質量\(m\)の物体Aが乗っています。\(t=0\)の初期状態で、Aの速さは\(v_o\)で右向き、Bは静止しています。Bと床との間には摩擦ははたらきませんが、AとBの間には摩擦があるものとします。

　この状態で、時刻\(t\)のAの速さは\(v\)、Bの速さは\(V\)であるとして、\(v\)と\(V\)の関係を求めてみます。

　摩擦力は非保存力ですから、A単独、または、B単独では力学的エネルギー保存則は成立しません。
それでも、AとBからなる系を考えた場合、力学的エネルギーの和は保存されるように、（間違って）思うかもしれません。
なぜなら、張力や抗力があっても、系の力学的エネルギーの和が保存される例を見てきたからです。

　それらの例では、張力や抗力が、ふたつの物体に同じ大きさで逆向きに作用するため、
ふたつの物体からなる系に対してされる仕事の和が\(0\)になっていました。

　この例でも、一見、張力や抗力の例と同じように、系の力学的エネルギーの和が保存されるように
思いますが、それは誤りです。
　それを、再び、運動エネルギーと仕事の関係から、確認してみましょう。

　図3-1のように、Bは\(t=0\)から\(t\)までの間に、\(L\)だけ移動し、
Aは、Bに対して、\(l\)だけ移動したものとします。

　仕事を求めるために用いる"距離"や、"速さ"には、系を構成するふたつの物体から離れたところで測定した値を用います。
つまり、Aの移動距離は\(L+l\)で、　Aが摩擦力からされる仕事は、（Aの進む方向と摩擦力の向きが逆であることを考慮して）　\(-\mu mg(L+l)\)です。
　この仕事により、Aの運動エネルギーが変化するので、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=-\mu mg(L+l) 　 \tag{3-1}
\end{equation}
同じように、Bが摩擦力からされる仕事は\(\mu mgL\)ですから、Bの運動エネルギーとの関係は、
\begin{equation} \frac{1}{2}MV^2-\frac{1}{2}M\times0^2=\mu mgL \tag{3-2}
\end{equation}

　(3-1)式と（3-2）式の両辺を足し合わせて、式を変形すると、次の式が得られます。
\begin{equation} \frac{1}{2}mv^2+\frac{1}{2}MV^2=\frac{1}{2}mv_o^2+\frac{1}{2}M\times 0^2-\mu mgl \tag{3-3}
\end{equation}

上の（3-3）式の左辺は、時刻\(t\)での運動エネルギーの和です。
右辺は、初期状態での運動エネルギーの和\(-\mu mgl\)となっているので、
力学的エネルギー（運動エネルギー）は保存されていないことがわかります。

　さて、このような設定の問題では、運動量の保存を使って解きます。
力積を用いて、この場合には運動量保存則が成り立つことを確認します。

　\(t=0\)から時刻\(t\)の間に、Aにはたらく力積は\(-\mu mgt\),
Bにはたらく力積は\(\mu mgt\)です。("\(\mu mg\)が一定であることに注意しましょう。）
運動量の変化量と力積は等しいことを式に表すと、
\begin{eqnarray}　　Aに対して&：& mv-mv_o=-\mu mgt \tag{3-4} \\
Bに対して&：& MV-M\times 0=\mu mgt \tag{3-5}
\end{eqnarray}

(3-4)式と（3-5）式の両辺をそれぞれ足して、式を変形すると、
\begin{equation} mv+MV=mv_o+M\times 0　　　\tag{3-6}
\end{equation}
となり、確かに運動量は保存されます。
　上の式から、
\begin{equation} V=\frac{m(v_o-v)}{M} \tag{3-7} \end{equation}

　この式は任意の時刻\(t\)において成り立つ\(v\)と\(V\)の関係式です。
時刻\(t\)が決まって始めて、\(v\)と\(V\)は一義的に求まりますが、
運動量保存則からだけでは、それらの値を求めることはできません。

　時刻\(t\) における\(v\)と\(V\)の値を求めるには、運動方程式を立てます。
時刻\(t\ )におけるAの加速度を\(\alpha\)、Bの加速度を\(\beta\)とすると、運動方程式は、
\begin{eqnarray} Aについて&：&　m\alpha=-\mu mg \tag{3-8} \\
Bについて&：&　M\beta=\mu mg \tag{3-9} \\
これより、\alpha&=&-\mu g \tag{3-10} \\
\beta&=&\frac{m}{M}\mu g \tag{3-11}
\end{eqnarray}

　以上より、\(t\) 秒後のA,Bの速度は、
\begin{eqnarray} v&=&v_o-\mu gt \tag{3-12} \\
V&=&\frac{m}{M}\mu gt \tag{3-13}
\end{eqnarray}

　さて、（3-12）、（3-13）式を使って、「この例題では力学的(運動)エネルギーが保存されない」ことをもう一度示してみましょう。
それには、［時刻\(t\)の運動エネルギーの和］-［[初期状態の運動エネルギーの和］が\(0\)にならないことを示します。
　（3-12）、（3-13）式を代入することで、

\begin{eqnarray} \frac{1}{2}mv^2&+&\frac{1}{2}MV^2-\left(\frac{1}{2}mv_o^2+\frac{1}{2}M\times 0^2 \right) \\
&=&\frac{1}{2}\frac{m^2}{M}\mu^2g^2t^2+\frac{1}{2}m\mu^2g^2t^2-\mu mgv_ot　\tag{3-14}
\end{eqnarray}

（3-10）、（3-11）式を使って、\(-\mu mgl\) の値を求めます。
\begin{eqnarray} -\mu mgl&=&-\mu mg\left(v_ot-\frac{1}{2}\mu gt^2-\frac{1}{2}\frac{m}{M}\mu mgt^2\right) \\
&=&-\mu mgv_ot+\frac{1}{2}m\mu^2g^2t^2+\frac{1}{2}\frac{m^2}{M}\mu^2g^2t^2 \tag{3-15}
\end{eqnarray}
　この式は、（3-14）式と等しくなりました。
このことから、運動方程式からも、（3-3）式、つまり「力学的エネルギー保存が成立しないこと」が示されました。

ところで、（3-15）式を見ると、右辺が\(0\)、つまり、力学的エネルギーが保存されるように見える瞬間があるように思われます。これは何を意味するのでしょうか。
　その時刻を\(t_1\)として、求めてみます。
\begin{eqnarray} -\mu mgv_ot_1+\frac{1}{2}m\mu^2g^2t_1^2+\frac{1}{2}\frac{m^2}{M}^mu^2g^2t_1^2=0 \\
これより、t_1=0、または、t_1=\frac{M}{M+m}\frac{2v_o}{\mu g}
\end{eqnarray}
　\(t_1=0\)は初期状態を意味しますから、力学的エネルギー保存の式が成り立っているように見えるのは当然です。
もうひとつの\(t_1\)は明らかに正の値ですから、もう少し吟味してみましょう。
（3-15）式の右辺が\(0\)ということは、時刻\(t_1\)で\(l=0\)ということです。
\(t=0\)で\(l=0\)ですが、その後、\(v\)のほうが\(V\)よりも大きいので、\(l\) は増加します。

　さらに時間が経過するとどうなるでしょうか。
仮に、\(v\lt V\)となることがあれば、\(l=0\)となる可能性があります。
　しかし、そうなる前に、\(v=V\)となった時点で摩擦がはたらかなくなり、その状態が維持されます。
したがって、\(v\lt V\)となることは現象的にはあり得ないことになります。

　確認しましょう。
\(v=V\)となるときの\(v\)を\(v_2\)とし、時刻\(t_1\)のときの\(v\)を\(v_1\)とし、両者を求め、\(v_1\lt v_2\)であることを確認します。
\(v_2\)を求めるには、運動量保存則から、
\begin{eqnarray} mv_o=mv_2+Mv_2 \\
v_2=\frac{mv_o}{m+M} \tag{3-16}
\end{eqnarray}
\(v_1\)は、
\begin{eqnarray} v_1=v_o-\mu gt_1=\frac{m-M}{m+M}v_o 　\tag{3-17} \\
(3-16)(3-17)式から、v_1-v_2=\frac{m-M}{m+M}v_o-\frac{mv_o}{m+M}=\frac{-M}{m+M}v_o \lt 0
\end{eqnarray}

以上のように、\(l=0\) が成立するときには、\(v_1\lt v_2\)です。
これは、「（3-14）式が成立するのは\(v\)と\(V\)が同じ値になるまで」、という条件があるのを無視して（3-14）式を適用したために、力学的エネルギーが保存される瞬間があるように見えたことが、わかります。

（3）　保存されない過程が入っている場合

　具体的な例を挙げます。

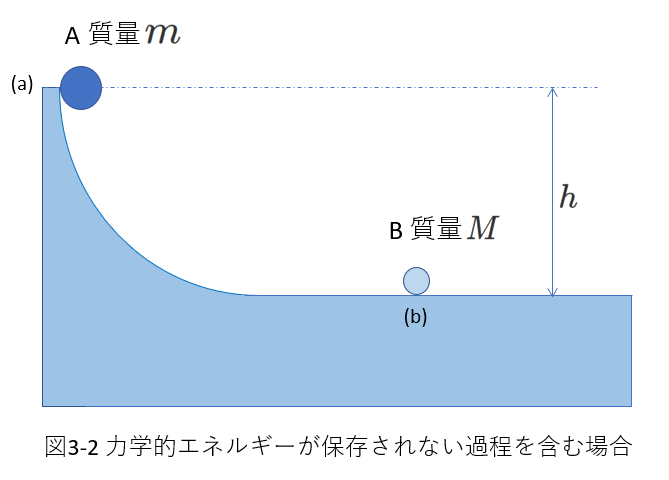
　図3-1で、質量\(m\)の物体Aが(a)の位置に保持されています。
今、Aを静かに放します。
下の台とAの間には摩擦はありません。
Aは台に沿って\(h\)の高さを滑り降りたあと、Bに接触し、その後AとBは一体化して進みました。
一体化して、進むときの速度の大きさを求めよ、というのが問題です。

　答えを出すためには、ふたつの過程に分けて考える必要があります。
イ．力学的エネルギーが保存される、衝突直前までの運動
ロ．運動量が保存されるが、力学的エネルギーは保存されない、衝突

　最初に、イの過程から、衝突直前のAの速さ\(v\)を求めます。
力学的エネルギーが保存される（垂直抗力はAに対して仕事をしません）ので、
[(a)でのAの力学的エネルギー]=[衝突直前のAの力学的エネルギー]
すなわち、
\begin{equation} \frac{1}{2}m\times 0^2+mgh=\frac{1}{2}mv^2+mg\times 0 \tag{3-17} \end{equation}
です。　ここで、(b)の位置を位置エネルギーの基準としています。
これより、
\begin{equation} v=\sqrt{2gh} \tag{3-18} \end{equation}
となります。

　次に、ロの過程を考えます。
衝突直後に一体化するということは、AもBも同じ速度になるということです。
（衝突後の相対速度が\(0\)という捉え方もできます。）
（また、一体化は衝突の特別な場合で、反発係数\(e=1\)の場合です。）
そこで、その速さを\(v'\)として、運動量保存の式を立てます。
\begin{eqnarray} mv+M\times 0&=&mv'+Mv' \tag{3-19}　\\
これより、 v'&=&\frac{mv}{m+M}=\frac{m}{m+M}\sqrt{2gh} \tag{3-20}
\end{eqnarray}
となります。

　この問題自身はそれほど難しい問題ではありません。
しかし、次のような間違いをする場合があります。
つまり、
(a)の位置から衝突後まで、力学的エネルギーが保存されると考え、
\begin{eqnarray} \frac{1}{2}m\times 0^2+mgh=\frac{1}{2}mv'^2+\frac{1}{2}Mv'^2+mg\times 0 \\
これより、v'=\sqrt{\frac{2mgh}{m+M}}=\sqrt{\frac{m}{m+M}}\sqrt{2gh}
\end{eqnarray}
とする誤りです。
(3-4)式との違いを確認してください。

　このような間違いをする原因として、次のようなことが考えられます。
物理では、問題は小問に分かれ、その小問により考察が順次誘導されます。
この形式に慣れると、いつの間にか、小問ひとつにひとつの公式あるいは原理を適用すればよいと錯覚するようになります。

　この例では、自分でふたつの過程にわけ、力学的エネルギーの保存則と運動量保存則のふたつを順番に適用して解くわけですが、ひとつの原理（力学的エネルギー保存則）を使って、この問題を最後まで解けるはずだと考えて、ミスをするようです。

　上の問題が、次のようなふたつの設問に分かれていれば、ほとんどの人はミスをしないでしょう。
設問1．衝突直前のAの速さを求めよ
設問2．衝突直後の一体化したAとBの速さを求めよ
このふたつの設問がひとつになった問題であると認識できれば、ミスをすることはありません。

Ⅳ．エネルギー保存則について再確認

　これまでの記事の内容をまとめ、注意すべきポイントを整理します。

（1）どの系で保存されるか

・単独で力学的エネルギーが保存される場合と、
　単独では保存されず、複数の物体からなる系において、力学的エネルギーの和が保存されるという場合があります。
・動くことができるふたつの物体が糸でつながれている場合や、接触している場合、それから、弾性衝突の場合には、力学的エネルギーの和の保存を検討します。

（2）　仕事とエネルギーの関係

・「仕事」と「エネルギー」とは、言葉は違いますが、単位は同じです。
　エネルギーは、「その物体が持つ、他の物体に対して仕事をする能力」を表しています。
　一方、仕事は、「力の大きさ」×「距離」で表される量です。
　単位が同じということは、仕事とエネルギーを足し引きできることを意味します。
・仕事をされた物体は運動エネルギーが変化します。
・非保存力に仕事された物体は、力学的エネルギーが変化します。

（3）非保存力がした仕事=力学的エネルギーの変化量

　非保存力が仕事をした場合、力学的エネルギーは保存されません。
しかし、「非保存力がした仕事」と力学的エネルギーの間には次の関係があります。
「非保存力が物体にした仕事」=「物体の力学的エネルギーの和の変化量」

（4）力学的エネルギー保存則を用いるメリット

・力や運動方程式を意識する必要がありまえせん。

　たとえば、"\(\frac{1}{2}mv^2+mgh=一定\)" の力学的エネルギー保存則において、
　\(mgh\)を "力×移動距離"と意識して立式する必要がありません。
　重力による位置エネルギーとして形式的に立式できます。

・離れたふたつの状態、あるいは、離れたふたつの時刻において力学的エネルギーが保存されると考えることができます。
　すなわち、ふたつの時刻の間の時間の出来事について、何も考える必要がありません。

Ⅴ．力学的エネルギー保存則の使い方

　これまでの記事の内容をまとめ、力学的エネルギー保存則を使う場合に注意すべきポイントを整理します。

（1）　[Aの状態の力学的エネルギー]=[Bの状態の力学的エネルギー]の形にする

　このとき、Aは、求めるべき未知数を含む状態を、
Bとしては、力学的エネルギーを簡単に表すことのできる状態を、自分で選びます。

（2）　単振動では、力学的エネルギー保存則と、単振動のエネルギー保存則を区別する

（3）「運動エネルギーと仕事の関係」と「力学的エネルギー保存則」との関係をしっかり理解すること

（4）重力による位置エネルギー（\(mgh\)）が使えるのは地表表面のみ

　地表を離れた場合は、万有引力による位置エネルギー\(\left(-G\frac{mM}{r}\right)\)を使います。

Ⅵ．力学的エネルギー保存則を用いる例題　　単独で保存される場合

(例1) 円筒内面を持つ台の上での鉛直面内円運動

　床の上に、円筒をちょうど半分で割った内面を持つ台が乗っています。
今、図6-1(a)の図に示すように質量\(m\)の物体Aを図の位置に保持し、
これを静かに離したあとの運動を考えます。
Ａと台の間には摩擦はないとし、台と床の間には摩擦があるとします。

　今、Aを放してから、図6-1(b)の\(\theta\)が\(\theta=0\)になるまで台は静止していたとして、
この間に床と台の間にはたらく摩擦力の最大値を求めます。

①物体Aと台にはたらく力を漏れなく図示します。
それが、図6-1(b)です。はたらく力を整理すると、
物体A：重力\(mg\)と台からの垂直抗力\(N\)
　　台：重力\(Mg\)とＡからの垂直抗力\(N\)と床からの垂直抗力\(N'\)と床からの摩擦力\(f\)
となります。

②運動を考察します。
　台は静止しているのですから、台にはたらく力は水平方向も鉛直方向もつりあっているはずです。
したがって、Aは鉛直面内で円運動をします。

③解法の見通しを立てます。
　\(f\)を求めるのが目的です。
\(f\)は台の水平方向の力のつりあいから求めることができそうです。
\(f\)以外で、水平方向の力の成分を持つのは、垂直抗力\(N\)だけです。
したがって\(N\)がわかれば\(f\)がわかりそうです。

　\(N\)は同じ大きさで向きが逆のちからがAにはたらいています。
Aは、円運動をしています。向心力は\(N\)と\(mg\)の円運動の中心向きの成分です。
このことから、円運動の運動方程式を立てれば、\(N\)がわかりそうです。
そのときに必要なAの速さは、力学的エネルギー保存則から求められそうです。

④立式
　③を逆にたどります。
力学的エネルギー保存則を考えます。
位置エネルギーの基準を台の上端とします。
図の角度\(\theta\)のときの上端からの鉛直方向の距離は\(r\cos\theta\)です。
したがって、力学的エネルギー保存を表す式は、
\begin{eqnarray} \frac{1}{2}m\times 0^2+mg\times 0&=&\frac{1}{2}mv^2+(-mgr\cos\theta) \tag{6-1} \\
\frac{1}{2}mv^2-mgr\cos\theta&=&0 \\
v&=&\sqrt{2gr\cos\theta} \tag{6-2}
\end{eqnarray}　

次に、円運動の方程式を立てます。
Aの速さは、（6-2）式で与えられ、また向心力は\(N-mg\cos\theta\)ですから、
\begin{eqnarray} m\frac{v^2}{r}&=&N-mg\cos\theta \tag{6-3} \\
N&=&m\frac{v^2}{r}+mg\cos\theta \\
&=&\frac{2mgr\cos\theta}{r}+mg\cos\theta \\
&=&3mg\cos\theta \tag{6-4}
\end{eqnarray}

　台について、水平方向の力のつりあいを考えて、
\begin{eqnarray} f&=&N\sin\theta \\
&=&3mg\cos\theta\sin\theta \\
&=&\frac{3}{2}mg\sin2\theta　\tag{6-5}
\end{eqnarray}
　（6-5）式から、\(f\) が最大値となるのは、\(\sin2\theta=1\)のときです。
つまり、\(\theta=\frac{\pi}{4}\)のとき、\(f\)は最大となり、最大値は\(f=\frac{3}{2}mg\)です。

　次に最大静止摩擦力を求めます。
台にはたらく力の鉛直方向成分のつり合いを考えると、
\begin{eqnarray} N'&=&Mg+N\cos\theta \\
&=&Mg+3mg\cos^2\theta
\end{eqnarray}
　したがって、最大静止摩擦力は、
\begin{equation} \mu N'=\mu (Mg+3mg\cos^2\theta)
\end{equation}
　最大静止摩擦力が最大となるのは、\(\cos\theta=1\)、すなわち、\(\theta=0\)のときです。
\(f\)が最大となる角度とは異なります。

　ある角度\(\theta\)で、台がとまったままでいられる条件は、
\begin{eqnarray} 3mg\cos\theta\sin\theta \leqq \mu (Mg+3mg\cos^2\theta) \\
\mu \geqq \frac{3m\cos\theta\sin\theta}{M+3m\cos^2\theta}
\end{eqnarray}
となります。

（例2）ふたつの振り子のおもりが衝突

　下の図6-2に示すように、ふたつの振り子があります。
どちらも質量\(m\)のおもりが糸で吊られています。糸の長さはどちらも\(l\)です。
ふたつの振り子の糸が鉛直方向になったとき、ふたつの重りはちょうど接するように配置されています。

　今、おもりAを糸をぴんと張った状態で、糸と鉛直方向がなす角が\(\theta\)となるまで持ち上げ、静かに放したとします。
Aは振り子の運動をして、Bに衝突、衝突後、Bは糸が鉛直面となす角度が\(\theta'\)になったところで速さが\(0\)となり、
その後、左に向かって動くものとします。
　ここで、\(\theta'\)を求めてみましょう。　具体的には、\(\cos\theta'\)を求めることにします。
ただし、AとBの反発係数(はね返り係数）を\(e\)とします。

①おもりA,Bにはたらく力を考えます。
　図示をするのが最良ですが、ここでは、図示せずに考えます。
A、および、Bにはたらく力は重力と糸の張力です。

②③運動を考察し、解法の見通しを立てます。
　(a)初期状態で、Aを放したとき、Aは糸につられているので、円運動をします。
鉛直面内の円運動ですね。
鉛直面内の円運動では、・力学的エネルギー保存則と、・円運動の運動方程式を立てるのが基本です。
Aには重力と張力がはたらきます。
重力は保存力、張力は非保存力ですが、張力とおもりの進む向きは垂直ですから、張力はおもりに対して仕事をしません。
以上の考察から、おもりAについて、力学的エネルギー保存則が成り立つことがわかります。

　これで、衝突直前のAの速さ\(v\)が求められそうです。
衝突ですから、おもりAとBからなる系について、運動量保存則が成り立ちそうです。

　運動量保存則が成立するには、系にはたらく力が内力だけで、外力なし、という条件が必要です。
AとBには、重力が働いていて、これは外力に相当します。
ただし、外力の向きは、鉛直下向きです。
一方、衝突直前直後のAとBの速度は、水平方向です。　　
重力は、水平方向の速さを変えることはないので、水平方向には運動量保存則が成り立つと考えることができます。

　衝突直後のAとBの速さをそれぞれ\(v'\)、\(V'\)とすると、運動量保存則と反発係数の式から、\(v'\)、\(V'\)を求めることができます。

　そして、速さ\(V'\)のおもりBがどこまで、上昇するかは、力学的エネルギー保存則から求めることができそうです。

④立式
　最初に、衝突直前のAの速さ\(v\)を求めます。
位置エネルギーの基準を初期状態のおもりBの位置に設けます。
力学的エネルギー保存則は、
\begin{eqnarray} [初期状態のAの力学的エネルギー]&=&[衝突直前のAの力学的エネルギー] \\
\frac{1}{2}m\times0^2+mgh&=&\frac{1}{2}mv^2+mg\times0 \tag{6-11} \\
ここで、h&=&l-l\cos\theta \\
\frac{1}{2}mv^2&=&mgh=mgl(1-\cos\theta) \\
v&=&\sqrt{2gl(1-\cos\theta)} \tag{6-12}
\end{eqnarray}

　次に衝突時の運動量保存則を立てます。
衝突直後のAの速さを\(v'\)、Bの速さを\(V'\)とします。
\begin{eqnarray} mv+m\times0=mv'+mV' \tag{6-13} \\
v=v'+V' \tag{6-14}
\end{eqnarray}

　反発係数の式は、反発係数を\(e\)として、
\begin{eqnarray} e&=&-\frac{V'-v'}{0-v} \tag{6-15} \\
ev&=&V'-v' \tag{6-16}　　　\\
(6-14)式+(6-16)式から、v+ev&=&2V' \\
V'&=&\frac{1+e}{2}v \tag{6-16}
\end{eqnarray}

　では、衝突後のBの運動に対して、力学的エネルギー保存則を考えて、
\begin{eqnarray} \frac{1}{2}mV'^2+mg\times0&=&\frac{1}{2}mv\times0^2 +mgh' \tag{6-17} \\
h'&=&l(1-\cos\theta') \\
\frac{1}{2}mV'^2&=&mgl(1-\cos\theta') \\
\cos\theta'&=&1-\frac{V'^2}{2gl} \\
&=&1-\frac{(1+e)^2v^2}{4\times2gl} \\
&=&1-\frac{(1+e)^2}{8gl}\times2gl(1-\cos\theta) \\
&=&1-\frac{1}{4}(1+e)^2(1-\cos\theta) \tag{6-18}
\end{eqnarray}

(6-18)式について検証しておきます。

(1) \(e=1\)の特別な場合を考えます。
つまり弾性衝突の場合（力学的エネルギー保存が成立する衝突です）で、このとき、
\begin{equation} \cos\theta'=1-\frac{1}{4}\times4 \times(1-\cos\theta)=\cos\theta \end{equation}
したがって、\(\theta'=\theta\)です。
このとき、（6-16）式から、\(V'=v\)、（6-14）式から、\(v'=V'-v=0\)です。
つまり、Aは衝突後は静止し、Bの衝突後の速さは、Aの衝突前の速さに等しく、BはAと同じ角度まで到達します。

(2) それでは、\(e=0\)の場合を考えてみましょう。
これは、（6-15）式から、直ちに\(v'=V'=\frac{1}{2}v\)であることがわかります。
衝突後の速さがAとBで同じです。
AとBが一体化したという問題設定のときによく用いられる設定です。このとき、
\begin{eqnarray} \cos\theta'&=&1-\frac{1}{4}\times1^2 \times(1-\cos\theta) \\
&=&\frac{3}{4}+\frac{1}{4}\cos\theta
\end{eqnarray}

　よくわからないので、\(\cos\theta-\cos\theta'\)を考えてみましょう。
\begin{eqnarray} \cos\theta-\cos\theta'&=&\cos\theta-\frac{3}{4}-\frac{1}{4}\cos\theta \\
&=&\frac{3}{4}\cos\theta-\frac{3}{4} \\
&=&\frac{3}{4}(\cos\theta-1)\leqq 0 \\
0\leqq \theta \leqq \frac{\pi}{2}、かつ、0\leqq \theta' \leqq \frac{\pi}{2} の範囲で考えれば、\theta\geqq \theta'
\end{eqnarray}
　これは、ごく常識的な関係です。

(3) 一般的な\(e\)の値のときの\(\cos\theta-\cos\theta'\)を考えてみます。

　（6-18）式から、
\begin{eqnarray} \cos\theta-\cos\theta'&=&\cos\theta-\left(1-\frac{1}{4}(1+e)^2(1-\cos\theta)\right) \\
&=&-(1-\cos\theta)+\frac{1}{4}(1+e)^2(1-\cos\theta) \\
&=&\frac{1}{4}(1-\cos\theta)(e-1)(e+3) \leqq 0 \\
&&ここで、0\leqq\cos\theta \leqq1、0\leqq e\leqq 1を用いました。 \\
&&　　　　　　　　　以上のことから、\cos\theta \leqq \cos\theta' \\
&&　　　　　　　　　0\leqq \theta \leqq \frac{\pi}{2} の範囲で考えれば、\theta \geqq \theta'
\end{eqnarray}
つまり、Bの角度は最初のAの角度以上にはなりません。
また、等号が成り立つのは、\(\cos\theta=1\)、または、\(e=1\)です。
（題意からは、\(\cos\theta=1\)、すなわち、\(\theta=0\)は考慮する必要はありません。）

　このことは、力学的エネルギーから考察するとわかります。
(a)初期状態から、(c)Bが最大に揺れた状態まで、力学的エネルギーが保存されるのは、
\(e=1\)の弾性衝突の場合だけでこのとき、\(\theta=\theta'\)となります。
　それ以外では、力学的エネルギーは減少します。
このとき、\(\theta \gt \theta'\)となります。

（例3）　鉛直面内の円運動

　図6-3では、質量\(m\)のおもりAが糸に結ばれ、糸の他端が点\(O\)に固定されています。
おもりAは鉛直面内で円運動をします。
今、Aが鉛直真下にあるとき、速さが\(V_0\)であったとします。
このとき、糸がぴんと張ったまま、鉛直真上に達することができる\(v_0\)の条件を求めてみましょう。

①おもりAにはたらく力を考えます。
図6-3では、糸の長さ方向と鉛直方向の角度が\(\theta\)のときの位置(b)で、Aにはたらく力を示してあります。
Aには重力と張力がはたらきます。
張力を\(T\)とします。
②③鉛直面内の円運動を考える場合には、力学的エネルギー保存則と円運動の運動方程式を使うのが基本です。
位置エネルギーの基準を(a)点として、力学的エネルギー保存を表す式は、
\begin{eqnarray} [(a)地点での力学的エネルギー]&=&［(b)地点での力学的エネルギー]　\\
\frac{1}{2}mv_o^2+mg\times0&=&\frac{1}{2}mv^2+mgl(1-\cos\theta) \\
\frac{1}{2}mv_o^2&=&\frac{1}{2}mv^2+mgl(1-\cos\theta) \tag{6-19} \\
v&=&\sqrt{v_0^2-2gl(1-\cos\theta)} \tag{6-20}
\end{eqnarray}

注）　（6-19）の位置エネルギーの項は三角関数を含むので間違えやすいと言えます。
正しいかどうかを簡単に見積もるには、特殊な場合を代入すると良いです。
\(\theta=0\)（鉛直真下）や\(\theta=\pi\)（鉛直真上）です。
　\(\theta=0\)（鉛直真下）では、\(mgl(1-\cos\theta)=0\)で、確かに(a)では位置エネルギーは\(0\)です。
\(\theta=\pi\)（鉛直真上）では、\(mgl(1-\cos\theta)=2mgl\)ですから、これも正しい値になっています。
どうやら、\(mgl(1-\cos\theta)\)は位置エネルギーを正しく表しているようです。
　また、図6-3の(b)の位置を想定して立式したわけですが、鉛直真上までの位置エネルギーが表現できているようです。

　　ここで注意するのは、(b)での速さを求めるには、力学的エネルギー保存則だけでOKということです。

　次に、円運動の運動方程式を立てます。
\begin{eqnarray} m\frac{v^2}{l}&=&T-mg\cos\theta \tag{6-21} \\
T&=&m\frac{v^2}{l}+mg\cos\theta \\
&=&\frac{m}{l}\left(v_0^2-2gl(1-\cos\theta)\right)+mg\cos\theta \\
&=&\frac{m}{l}v_0^2-2mg+3mg\cos\theta \tag{6-22}
\end{eqnarray}
　このように、円運動の運動方程式から、糸の張力を求めることができます。

　さて、(6-22)式を見ると、\(\theta\)が\(0\)から\(\pi\)まで変化すると、\(\cos\theta\)は\(1\)から\(-1\)に変化します。
つまり、\(\theta=\pi\)のとき\(T\)は最小になります。
\(\theta=\pi\)で\(T\geqq0\)が鉛直真上まで糸がたるまない条件ですから、
\begin{eqnarray} T&=&\frac{m}{l}v_0^2-2mg+3mg(-1) \geqq 0 \\
\frac{m}{l}v_0^2&\geqq&5mg \\
v_0&\geqq&\sqrt{5lg} \tag{6-23}
\end{eqnarray}

　また、おもりAが鉛直真上に達する条件を、\(\theta=\pi\)で\([運動エネルギー]\geqq0\)として求めます。

\begin{eqnarray} \frac{1}{2}mv^2&=&\frac{1}{2}mv_0^2-mgl(1-\cos\theta) \\
&=&\frac{1}{2}mv_0^2-2mgl\geqq0 \\
v_0&\geqq&\sqrt{4gl} \tag{6-24}
\end{eqnarray}

　したがって、糸がたるむことなく、Aが鉛直真上に到達する条件は、（6-23）式、かつ、（6-24）式ですから、結局（6-23）式が答えになります。

Ⅶ．力学的エネルギー保存則を用いる例題　　2個以上からなる系で保存される場合

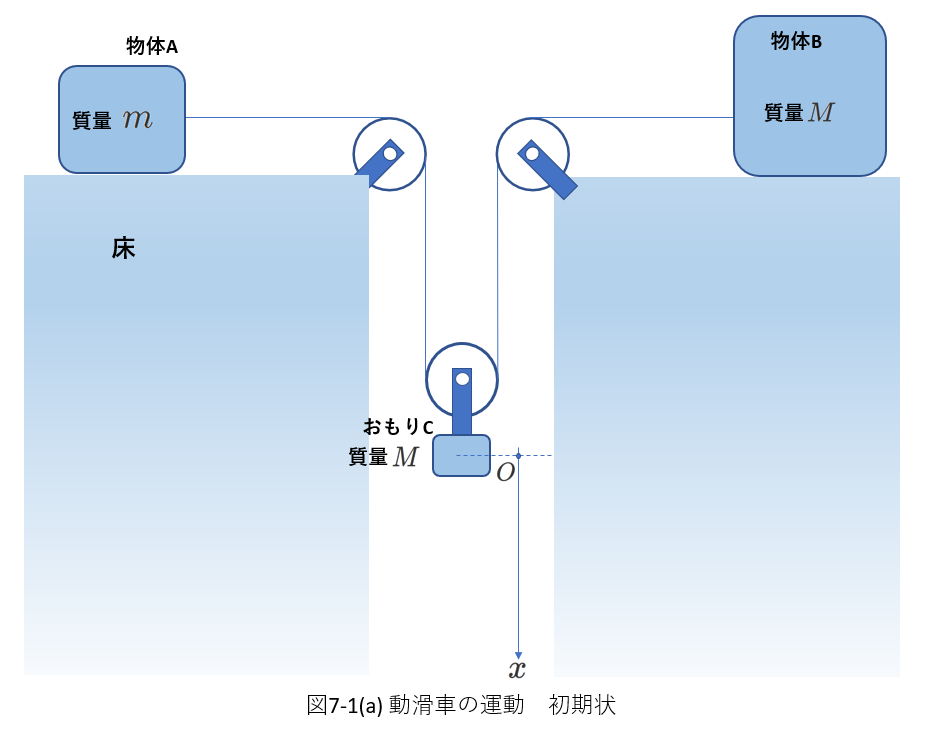
(例1) 動滑車と2個の物体の運動

　右の図7-1(a)のように、物体A,物体BとおもりCが配置されています。
AとBは糸でつながれています。
そして、その糸は動滑車に通されています。

　物体A,Bと台の間には摩擦はなく、滑車や糸の質量は無視できるものとします。
　おもりが下降しないように、
糸がぴんと張った状態でおもりは支えられています。
このときのおもりの位置を\(x\)軸の原点とします。
\(x\)軸の正の向きを下向きとします。

　時刻\(t=0\)で支えを外したときの、物体A,物体BとおもりCの運動を考察します。
おもりCの\(x\)座標が\(h\)のときの、おもりCの速さを求めます。

　図7-1(b)は、おもりCが\(h\)下降した状態を表しています。
物体Aの速さを\(v_1\)、物体Bの速さを\(v_2\)、おもりの速さを\(v\)とします。
A,B,Cにはたらく力の一部を図7-1(b)に示しました。
重力は保存力、張力\(T\)は非保存力ですが、A,B,Cにする仕事の和は\(0\)となり、
力学的エネルギーの和は保存されるようです。重力による位置のエネルギーの基準を原点\(O\)にとります。

　そこで、力学的エネルギー保存の式を表すと次のようになります。
\begin{eqnarray} \frac{1}{2}m\times 0^2+\frac{1}{2}M\times 0^2+\frac{1}{2}M\times 0^2+Mg\times 0&=&\frac{1}{2}mv_1^2+\frac{1}{2}Mv_2^2+\frac{1}{2}Mv^2-Mgh \\
\frac{1}{2}mv_1^2+\frac{1}{2}Mv_2^2+\frac{1}{2}Mv^2-Mgh&=&0 \tag{7-1}
\end{eqnarray}

　また、おもりCが\(h\)下降したときの、Aの移動距離を\(a\)、Bの移動距離を\(b\)とすれば、
次の関係があります。
\begin{equation} 2h=a+b \tag{7-2} \end{equation}
\(a,b.h\)を時間\(t\)で微分すれば、
\begin{equation} 2v=v_1+v_2 \tag{7-3} \end{equation}

　未知数は、\(v_1,v_2,v\)の３つですから、（7-1）（7-3）式の2つの式だけでは、解くことができません。
この問題の3個の物体からなる系では、力学的エネルギー保存則から\(v\)を求めることはできないようです。

[参考]　力学的エネルギーが保存されることを確認する

念のため、A,B,Cの系で力学的エネルギーが保存されることを示しておきましょう。
非保存力は張力の\(T\)だけですから、
\(T\)が系にする仕事の和が\(0\)であることを示せば、力学的エネルギーが保存されることを示したことになります。

\begin{eqnarray}
　Tが物体Aにする仕事&は&、Ta \\
Tが物体Bにする仕事&は&、Tb \\
　TがおもりCにする仕事&は&、-2Th \\
　Tが系にする仕事の和&は&、Ta+Tb-2Th=T(a+b-2h)=0
\end{eqnarray}
　上の式の変形では、（7-2）式を用いました。
　以上のように、A,B,Cの系を考えれば、力学的エネルギーは保存されることがわかりました。

[別解]　運動方程式から考える

力学的エネルギー保存で解ける問題は、多くの場合、運動方程式を使っても解けます。
そこで、運動方程式を立てて考えてみます。
\begin{eqnarray} Aについて&:&m\alpha_1=T \tag{7-4} \\
Bについて&:&M\alpha_2=T \tag{7-5} \\
Cについて&:&M\alpha=Mg-2T \tag{7-6} \\
３つの式の各辺同士の和を取って、Tを消去すると&、& m\alpha_1+M(\alpha_2+\alpha)=Mg \tag{7-7}
\end{eqnarray}

　（7-2）式を参考にすると、
\begin{equation} 2\alpha=\alpha_1+\alpha_2 \tag{7-8} \end{equation}

　(7-4)(7-5)(7-6)式を（7-8）に代入すると、
\begin{eqnarray} 2\left(g-\frac{2T}{M}\right)=\frac{T}{m}+\frac{T}{M} \tag{7-9} \\
これより、T=\frac{2mMg}{M+5m} \tag{7-10}
\end{eqnarray}

　（7-10）式を（７-6）に代入して、\(\alpha\)を求めると、
\begin{eqnarray} \alpha&=&g-\frac{2}{M}T \\
&=&g-\frac{2}{M}\frac{2mMg}{M+5m} \\
&=&\frac{M+m}{M+5m}g \tag{7-11}
\end{eqnarray}

　これより、
\begin{eqnarray} v^2-0^2&=&2\alpha h \tag{7-12} \\
v&=&\sqrt{2\alpha h} \\
&=&\sqrt{\frac{2hg(M+m)}{M+5m}}
\end{eqnarray}
　以上のように、運動方程式から、この問題を解くことができます。

物理の大学入試問題を解く