運動エネルギーと仕事の関係

トップページ＞力学＞運動エネルギーと仕事の関係

Ⅰ．運動エネルギーと仕事の関係

　質量\(m\)の物体に\(W\)の仕事がされ、物体の速さが、\(v_o\)から\(v\)に変わったとき、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=W 　\tag{１-1}　\end{equation}
の関係が成り立ちます。

この章では、運動方程式から（1-1）式を導きます。
なお、（1-1）式は、常に成り立ちます。
一方、力学的エネルギー保存則や運動量保存則は、成立しない場合があります。

（1）準備

物体が加速度\(a\)で、\(x\)軸上を等加速度直線運動をしている。
時刻\(t=0\)での速度を\(v_o\)、\(x\)座標を\(x_o\)とし、
時刻\(t\)での速度を\(v\)、\(x\)座標を\(x\)とすると、
\begin{eqnarray} v=v_o+at \tag{1-2} \\
x=x_o+v_ot+\frac{1}{2}at^2 \tag{1-3} \end{eqnarray}
この2式から、
\begin{equation} v^2-v_o^2=2a(x-x_o) \tag{1-4} \end{equation}

【参考】（1-4）式の導出
\begin{eqnarray}
(1-3)式を変形して、x-x_o&=&t\left(v_o+\frac{1}{2}at\right) \tag{1-5} \\
(1-2)式から、t&=&\frac{v-v_o}{a}　\\
これを(1-5)に代入して(1&-&4)が求められます。
\end{eqnarray}

（2）　運動方程式から「運動エネルギーと仕事の関係」を導出

　右図のように、質量\(m\)の物体に大きさ\(F\)の力がはたらいているとします。
この場合、加速度を\(a\)として、運動方程式\(ma=F\)が成立します。

　（1-4）式の両辺に\(\frac{1}{2}m\)を掛けて
\begin{eqnarray} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2&=&\frac{1}{2}2ma(x-x_o) \\
\\
ここで、ma=F、x-x_o&=&l ですから、　\\
\frac{1}{2}mv^2-\frac{1}{2}mv_o^2&=&Fl \tag{1-6} \\
\\
Flは仕事を表すので、Fl&=&Wとして、 \\
\frac{1}{2}mv^2-\frac{1}{2}mv_o^2&=&W \tag{1-7} \\
\end{eqnarray}

【まとめ】

質量\(m\)の物体に\(W\)の仕事がされ、物体の速さが、\(v_o\)から\(v\)に変わったとき、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=W 　\tag{１-5}　\end{equation}
　物体にはたらく力\(F\)が一定で変位が\(l\)として、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=Fl 　\tag{１-4}　\end{equation}

　「運動エネルギーと仕事の関係」を表す（1-4）（1-5）式は、常に成り立ちます。
一方、力学的エネルギー保存則は、成立しない場合があります。

　問題を解く際には、
（１）力学的エネルギー保存　（２）「運動エネルギーと仕事の関係」　（３）運動方程式
の順序で検討しましょう。

（3）問題を考える3つの方法
(3-1) 「運動エネルギーと仕事の関係」は次式、あるいは、（1-7）式で表されます。
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=Fl 　\tag{１-6}　\end{equation}
　これを用いて解く問題は、

・力\(F\)で\(l\) 移動した後の速度を求める
・速度の変化から、移動した距離を求める
・速度の変化から、力がした仕事を求める

　などが、考えられます。

　「運動エネルギーと仕事の関係」の特徴は、時間の要素がないという点です。
　（この点は、運動エネルギー保存則や運動量保存則も同じです。）
　したがって、時間を求める必要のない問題には、とても有力なツールです。

(3-2)　同じような力を発揮する2つめの解法は、
\begin{equation} v^2-v_o^2=2a(x-x_o)=2al \tag{1-4} \end{equation}　　
を使う方法です。

　この式にも時間の要素がないことに注目してください。
　また、（「運動エネルギーと仕事の関係」の導出過程を追えばわかりますが）
（1-6）式と（1-4）式は非常によく似ていて、同じように使うことができます。

　異なるのは、「運動エネルギーと仕事の関係」の（1-6）式は、力\(F\)、
（1-4）式は、加速度\(a\)が使われてることです。
したがって、（1-4）式を使うためには、加速度を求めるために
運動方程式を立てる必要があります。

(3-3) 3つめは、運動方程式と（1-2）（1-3）式をセットで使う方法です。

　運動方程式を立て、加速度を求めます。
加速度が一定であれば、次の式が成り立ちます。

\begin{eqnarray} v=v_o+at \tag{1-21} \\
x=x_o+v_ot+\frac{1}{2}at^2 \tag{1-3} \end{eqnarray}

　・\(l\) 変位したときの速度を求めるには、
　　最初に、（1-3）式で、\(x=x_o+l\)として、\(t\)を求めます。
　　この\(t\)を（1-2）式に代入すれば、求める速度\(v\)が求められます。

　・速度が\(v_o\)から\(v'\)になるまでの間に移動した距離を求めるためには、
　　（1-2）式で\(v=v'\)として、\(t\)を求めます。
　　これを（1-3）式に代入し、\(x-x_o\)を求めます。

Ⅱ．３つの例について、運動エネルギーと仕事の関係を考える

　3つの例を考え、「運動エネルギーと仕事の関係」や「仕事」と「位置エネルギー」との関係を理解します。　

（1）　運動エネルギーと仕事の関係＿正の仕事

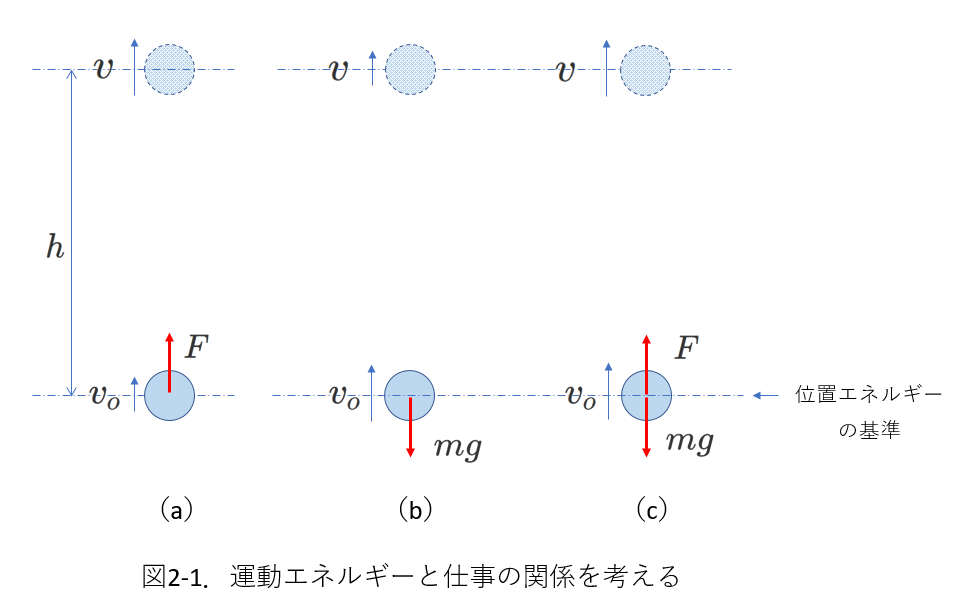
　最初の例は、下図2-1の（a）です。
質量\(m\)の物体が力\(F\)を受けて、水平面上を\(h\)の距離進みます。

　水平面上の運動であるので、重力の影響を考える必要はありません。
　初速を\(v_o\)、距離\(h\)進んだ時の速度を\(v\)として、
「運動エネルギーと仕事の関係」を表す式は、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=Fh \tag{2-1} \end{equation}

　物体が移動する方向と力\(F\)の向きが同じなので、仕事\(Fh\)は正ですから、
\begin{eqnarray} \frac{1}{2}mv^2&\gt&\frac{1}{2}mv_o^2 \\
v&\gt& v_o \\ \end{eqnarray}
つまり、物体は\(F\)から正の仕事をされて、速さが増加しました。

注）　（2-1）式を力学的エネルギー保存の式と考える人がいますが、
　　この式は、力学的エネルギー保存を表す式ではありません。

　　　\(F\)のした仕事が失われないで物体の運動エネルギーの中に保存されると考えて、保存を表す式と考えるようですが、間違いです。
　　力学的エネルギー保存則とは、「時間の経過にかかわらず、常に力学的エネルギーは一定」ということです。

　　　図2-1．（ａ）の初期状態の力学的エネルギーは\(\frac{1}{2}mv_o^2\)、
　　\(h\)移動したあとの力学的エネルギーは\(\frac{1}{2}mv^2\)ですから、
　　（2-1）式は、\(Fh\)の仕事をされたことにより、力学的エネルギーが、
　　\(\frac{1}{2}mv_o^2\)から\(\frac{1}{2}mv^2\)に増加した、ということを表しています。

（2）　運動エネルギーと仕事の関係＿負の仕事

　上図2-1の（b）の場合を考えます。
今度は鉛直面に沿った運動で、物体が鉛直上向きに動いています。
物体にはたらく力は重力だけです。
初速は\(v_o\)、\(h\)上昇した瞬間の速度を\(v\)とします。

　重力が物体にした仕事は、物体が進む向きと重力の向きが逆ですから、\(-mgh\)です。

　したがって、「運動エネルギーと仕事の関係」を表す式は、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=-mgh \tag{2-2} \end{equation}
となります。

　\(-mgh\lt 0\)ですから、
\begin{eqnarray} \frac{1}{2}mv^2&\lt&\frac{1}{2}mv_o^2 \\
v&\lt& v_o \\ \end{eqnarray}
つまり、物体は重力\(mg\)から負の仕事をされて、速さが減少しました。

ところで、(2-2)式は次のように書き換えられます。
\begin{equation} \frac{1}{2}mv^2+mgh=\frac{1}{2}mv_o^2 \tag{2-2'} \end{equation}

　この式は、初期状態の高さを重力の位置エネルギーの基準として、
　[高さ\(h\)での、物体の力学的エネルギー（運動エネルギー+位置エネルギー）]=[初期状態での物体の力学的エネルギー]
つまりは、力学的エネルギーの保存則を表していることがわかります。

　つまり、重力のような保存力のみが作用する場合は、
力学的エネルギーの保存則を表す式と「運動エネルギーと仕事の関係」に着目して立てた式は同値の式になります。
したがって、このような場合に問題を解く場合は、力学的エネルギーの保存則を使って式を立てます。
　問題によっては、わざわざ重力のした仕事を求めさせ、
その後、「運動エネルギーと仕事の関係」に誘導するものがあります。
問題の指示にしたがいましょう。

また、（2-2'）式において、\(\frac{1}{2}mv^2\geqq 0\)です。
　（2-2'）式を変形して、
\begin{eqnarray} \frac{1}{2}mv^2=\frac{1}{2}mv_o^2-mgh&\geqq& 0 \\
\frac{1}{2}mv_o^2&\geqq& mgh \\
h&\leqq& \frac{v_o^2}{2g}
\end{eqnarray}
　これは、\(h\)の取り得る範囲を示しています。
　すなわち、物体が存在できる範囲は、運動エネルギーが\(0\)以上になる場所です。
存在できる境界は、運動エネルギーが\(0\)、すなわち、速さが\(0\)になるところです。　

　最高点では、速度が\(0\)（運動エネルギーが\(0\)）になると、考えても良いです。

　力学的エネルギー保存則から、上記のように、物体の存在できる範囲を求める問題は非常に多いです。
たとえば、宇宙船が宇宙の果てに到達できるかどうかを確認する問題などです。

（3）　運動エネルギーと仕事の関係＿つりあったふたつの力のする仕事　

　今度の例は、下図2-1の（c）の場合です。

　今度も鉛直面に沿った運動で、物体が鉛直上向きに動いています。
物体にはたらく力は重力\(mg\)と外力\(F\)です。
そして、このふたつの力はつりあっていて、\(mg=F\)です。
初速は\(v_o\)、\(h\)上昇した瞬間の速度を\(v\)とします。

　力がつりあっていて物体が動くのはおかしいと思ったかもしれませんが、
力がつりあっていた状態で、物体が動くということは、等速度運動をしているということです。

　さて、（1）（2）を参考にして、
重力\(mg\)が物体にした仕事は\(-mgh\)、外力\(F\)が物体にした仕事は\(Fh\)です。

　したがって、「運動エネルギーと仕事の関係」を表す式は、
\begin{equation} \frac{1}{2}mv^2-\frac{1}{2}mv_o^2=-mgh+Fh \tag{2-3} \end{equation}
　（2-3）式の右辺は、\(mg=F\)により、\(0\)ですから、
\begin{eqnarray} \frac{1}{2}mv^2&=&\frac{1}{2}mv_o^2 \\
v&=& v_o \\ \end{eqnarray}

　つまり、物体は同じ大きさの正と負の仕事をされたので、速度は変化しません。　
　力がつりあった状態の物体の運動は、等速度運動であり、運動エネルギー(速度）は変化しないことを
あらためて、確認したと言えます。
　また、外力\(F\)を受けているので、力学的エネルギーは保存されません。

上で説明したように、運動エネルギーは変化しないので、（2-3）式の右辺は\(0\)です。
\begin{eqnarray} つまり、0&=&-mgh+Fh \\
Fh&=&mgh
\end{eqnarray}
このことは、外力\(F\)は位置のエネルギーを\(mgh\)だけ高めるために使われたと解釈できます。

【まとめ】
　力がする仕事には正と負の場合があります。
　どちらも、「運動エネルギーと仕事の関係」に表すことができます。
　物体は正の仕事を受けて（物体が進む向きの力を受けて）、速度は増加、
　負の仕事を受けて（物体が進む向きと逆向きの力を受けて）、減少します。

Ⅲ．「運動エネルギーと仕事の関係」をもう一度考える

　「Ⅱ．３つの場合について、運動エネルギーと仕事の関係を考える」に続いて、
さらに、具体的な3例について、「運動エネルギーと仕事の関係」を考えます。

（1）自由落下

　物体の自由落下を考えます。
鉛直方向に\(x\)軸をとり、下向きを正の向きとします。
原点\(O\)で初速\(0\)で物体を放します。

　\(x=h (\gt 0)\)での速さ\(v\)を求めます。

　物体には重力がはたらいています。
この重力が物体にした仕事は、\(mg\times h\)です。
運動エネルギーの変化は、\(\frac{1}{2}mv^2-\frac{1}{2}m\times 0^2\)ですから、

「運動エネルギーと仕事の関係」から
\begin{eqnarray} \frac{1}{2}mv^2-\frac{1}{2}m\times 0^2&=&mgh \tag{3-1} \\
v&=&\sqrt{2gh}
\end{eqnarray}
となります。

さて、この問題自体は、力学的エネルギー保存則から解くことができます。
物体にはたらく力は、保存力の重力だけですから、力学的エネルギーは保存されます。
そこで、重力による位置エネルギーの基準を原点\(O\)にとって
［原点\(O\)での力学的エネルギー］=［\(x=h\)での力学的エネルギー]　という式を立てると、
\begin{equation} \frac{1}{2}m\times 0^2+mg\times 0=\frac{1}{2}mv^2+(-mgh) \tag{3-2} \end{equation}
この式は、（3-1）式と同値です。

　\(x=h\)での位置のエネルギーが\(-mgh\)で表されます。
基準より下の位置ですから、位置のエネルギーは負、
\(x\)軸の正の向きが下向きで\(h>0\)ですから、\(-mgh\)という表現になります。

　この問題を解くには、通常、「運動エネルギーと仕事の関係」を考えるのではなく、
力学的エネルギー保存を用います。

（2）ばねの伸縮

　ばねに質量\(m\)のおもりがつながっています。
ばねの自然長から\(l\)だけ縮め、そっと放したとき、ばねが自然長に戻った瞬間の速さ\(v\)を求めます。
おもりを放したときのおもりの運動の向きを\(x\)軸の正の向きとします。
放す瞬間のおもりの位置を\(x\)軸の原点とします。

　この問題も、「運動エネルギーと仕事の関係」を用いて解くことができます。
おもりを放す瞬間から、ばねが自然長に戻るまでの運動エネルギーの変化は、
\(\frac{1}{2}mv^2-\frac{1}{2}m\times 0^2\) です。

　ばねから受ける弾性力がおもりにする仕事を考えます。
「（1）自由落下」で重力のする仕事を\(mgh\)と書けたのは、重力\(mg\)が物体の位置によらず一定であったため、
仕事を[力]×[移動距離]と表すことができました。

　しかし、ばねの弾性力はばねの伸縮量（したがって、おもりの位置/座標）によって変化します。
このときに仕事をどのように計算するかが、この問題のポイントです。

　この仕事は、グラフを使って解きます。
以下の考えは積分を考える場合と同じで、積分を使って考えることもできます。

　右図3-3を見てください。
(a）はおもりの位置とばねの弾性力の大きさの関係を示しています。
弾性力は、\(x\)座標を用いて、\(y=k(l-x)\)と表されます。

　さて、仕事は[力]×[移動距離]ですから、
（b）のように、力の大きさが一定とみなせるほど短い移動距離\(\Delta x\)を考えれば、
仕事は、\(k(l-x)\Delta x\)となります。
この短冊の面積を\(x=0\)から\(x=l\)まで足せばよいので、
（c）に示すように、ばねの弾性力がこの間におもりに対してする仕事は、斜線で表した部分の面積に等しくなります。

　この面積は、\(\frac{1}{2}kl^2\)ですから、
「運動エネルギーと仕事の関係」を表す式は、
\begin{eqnarray} \frac{1}{2}mv^2-\frac{1}{2}m\times 0&=&\frac{1}{2}kl^2 \tag{3-3} \\
v&=&\sqrt{\frac{k}{m}}l \tag{3-4}
\end{eqnarray}
となります。

さて、この問題も、普通は力学的エネルギー保存則から解きます。
物体にはたらく力は、保存力の重力と弾性力ですから、力学的エネルギーは保存されます。
そこで、
［放す瞬間（原点\(O\)で）の力学的エネルギー］=［\(x=ｌ\)での力学的エネルギー]　という式を立てると、
\begin{equation} \frac{1}{2}m\times 0^2+\frac{1}{2}kl^2=\frac{1}{2}mv^2+\frac{1}{2}k\times 0^2 \tag{3-5} \end{equation}
この式は、（3-3）式と同値です。

（3）摩擦力
　床の上を物体が運動していて、物体と床の間には摩擦があります。
右向きに\(x\)軸の正の向きをとり、原点\(O\)での速さが\(v\)のとき、\(x=h(\gt0)\)での速さ\(v'\)を求めます。

　物体の運動エネルギーの変化は、\(\frac{1}{2}mv'^2-\frac{1}{2}mv^2\)、
物体と床の間にはたらく垂直抗力は\(mg\)、したがって、動摩擦係数を\(\mu\)として、摩擦力の大きさは\(\mu mg\)です。
摩擦力は左向き、物体の運動は右向きですから、
摩擦力が物体にする仕事は、\(-\mu mgh\)です。

　このことから、「運動エネルギーと仕事の関係」を表す式は、
\begin{eqnarray} \frac{1}{2}mv'^2-\frac{1}{2}mv^2=-\mu mgh \tag{3-6} \\
v'=\sqrt{v^2-2\mu gh}
\end{eqnarray}

注）　（3-6）式は、力学的エネルギー保存則の式ではありません。
　（3-6）式は、摩擦力により、力学的エネルギーが変化する、という式です。
　力学的エネルギー保存則は、
　[状態Aでの力学的エネルギー]=[状態Bでの力学的エネルギー]となりますが、
　図3-4の例では、
　[原点Oでの物体の力学的エネルギー]\(\neq\)[物体が\(x=h\)を通過する瞬間の力学的エネルギー]です。

さて、（1）自由落下、（2）ばねの伸縮では、力学的エネルギー保存則が成り立つので、
「運動エネルギーと仕事の関係」を使わなくても、力学的エネルギー保存則を使って問題を解くことができました。

　（3）摩擦力では、注）で説明したように、力学的エネルギー保存則は使えません。
　それでも、「運動エネルギーと仕事の関係」を用いずに、この問題を解くことは可能です。

　それには、運動方程式を立てて、加速度を求めます。
続いて、等加速度運動の次の公式の3番目の式を用います。

\begin{eqnarray} v&=&v_o+\alpha \\
x&=&x_o+v_o t+\frac{1}{2}\alpha t^2 \\
v^2-v_o^2&=&2\alpha\left(x-x_o\right) \\
\\
ただし、時刻t&=&0での速度はv_o、y座標はy_0、　\\
時刻t&で&の加速度は\alpha=\frac{F}{m}、速度はv、x座標はx、速度と加速度は+xの向きが正
\end{eqnarray}

　加速度を\(a\)として、運動方程式は、\(ma=-\mu mg\)、
したがって、\(a=-\mu g\)
これより、\(v'^2-v^2=2ah\)から、\(v'=\sqrt{v^2-2\mu gh}\)となります。

　以上をまとめれば、
・「運動エネルギーと仕事の関係」を使って解ける問題は、力学的エネルギー保存則や運動方程式を使っても解けます。
・力学的エネルギー保存則は成立しない場合がありますが、「運動エネルギーと仕事の関係」は常に成り立ちます。
・「運動エネルギーと仕事の関係」を要求する問題もあるので、理解しておきますしょう。

Ⅳ．例題

（1）　例題1

　台上に物体A（質量\(M\)）が置かれています。

Aには糸が結び付けられ、糸のもう一方の端は台の角に設置された滑車を通して、物体B（質量\(m\)）につながれ、Bを吊っています。

　今、物体Aを押さえておき、
時刻\(t=0\)で放したとします。

すると、Aは右向きに、Bは下向きに動き出します。
物体Aと台との間には動摩擦力がはたらくものとします。
糸が伸縮したり、たるむことはないとして、物体Bが\(L\)の距離落下したときの、速さを求めてみましょう。

【運動方程式を用いる】

　糸は伸縮したりたるんだりすることはないとすると、
物体AとBでは、移動距離も速度も加速度も同じです。
そこで、運動中の物体AとBの加速度を\(\alpha'\)とします。

　物体Aと物体Bにはたらく力は図4-1に示されているとおりです。

　物体Ａにはたたく力は、
・重力　\(Mg\)
・糸の張力　\(T'\)
・台からの垂直抗力　\(N\)　
　物体Aは水平方向右向きに動くだけで、鉛直方向には動きません。
　したがって、鉛直方向の力はつりあっているはずで、\(N=Mg\)となります。
・台との間の動摩擦力　\(\mu N=\mu Mg\)

　物体Bにはたらく力は、
・重力　\(mg\)
・糸からの張力　\(T'\)

　解法の方針は、
運動方程式から加速度を求め、
（等加速度運動であると予想できるので）
等加速度運動の公式を使って、加速度と落下距離から速さを求めます。

　それでは、運動方程式を立ててみます。
Aについては、右向きを加速度の正の向き、
Bについては、下向きを加速度の正の向き、と考えます。

\begin{eqnarray}
　A&：&Ma'=T'-\mu Mg \tag{4-1} \\
B&：&ma'=mg-T' \tag{4-2}
\end{eqnarray}

これから加速度\(\alpha'\)を求めます。
（4-1）式+（4-2）式を計算すると、
\begin{eqnarray} (M+m)\alpha'&=&mg-\mu Mg \\
\alpha'&=&\frac{(m-\mu M)g}{M+m}　\tag{4-3}
\end{eqnarray}　　

　さて、加速度\(\alpha'\)で距離\(L\)移動したとき、
AおよびBの速さは\(0\)から\(v\)に変化したとすると、

\begin{eqnarray} v^2-0^2=2\alpha' L \tag{4-4} \\
v=\sqrt{\frac{2(m-\mu M)gL}{M+m}} \tag{4-5}
\end{eqnarray}

【「運動エネルギーと仕事の関係」を用いる】

　糸は伸縮したりたるんだりすることはないとすると、
物体AとBでは、移動距離も速度も加速度も同じです。
距離\(L\)移動したときのA,Bの速さを\(v\)とします。
A,Bとも初速度は\(0\)です。

　物体Aと物体Bにはたらく力は図4-1に示されているとおりです。

　物体Bにはたらく力は、
・重力　\(mg\)
・糸からの張力　\(T'\)

　解法の方針は、
「運動エネルギーと仕事の関係」の式を、A、Bについて立てます。
未知数は、\(v\)と\(T'\)です。
「運動エネルギーと仕事の関係」の式は2つできるので、\(T'\)を消去し、\(v\)を求めることができそうです。

　それでは、「運動エネルギーと仕事の関係」の式を立てます。

\begin{eqnarray} A&：&\frac{1}{2}Mv^2-\frac{1}{2}M\times 0^2=(T'-\mu Mg)L \tag{4-6} \\
B&：&\frac{1}{2}mv^2-\frac{1}{2}m\times 0^2=(mg-T')L \tag{4-7}
\end{eqnarray}

　（4-6）式+（4-7）式を計算します。

\begin{eqnarray} \frac{1}{2}(M+m)v^2=(mg-\mu Mg)L \tag{4-8} \\
v=\sqrt{\frac{2(m-\mu M)gL}{M+m}} \tag{4-9}
\end{eqnarray}

　こちらの解法では、加速度を求める必要がないので、
その分計算が少なくて済みます。

（2）　例2

　球A（質量\(m\)）が物体B（質量\(M\)）を貫通する問題です。
Bに接触する直前のAの速度は\(v\)、Bは静止しているとします。
物体Bの長さを\(l\)として、貫通直後のAの速度を\(v'\)、Bの速度を\(V'\)とします。
\(v'\)を、\(v,V',m,M\)を使って表すことが、問題です。

注）\(v'とV'\)の両方を求めるためには、条件がもう一つ必要です。　そこで、ここでは、\(V'を使ってv'\)を表すという問題にしました。

　なお、図4-2（b）に示されているように、
球Aが物体Bの中にあるとき、AとBは常に一定の力（大きさ\(f \)）を及ぼしあうと考えます。また、床とBの間には摩擦はないとします。

【運動量保存則を用いる】

　球Aと物体Bにはたらく水平方向の力は\(f\)だけです。
重力は鉛直方向にしかはたらかないので、速度の水平方向成分には影響を与えません。
AとBは\(f\)を及ぼし合う関係なので、AとBからなる系を考えたとき、\(f\)は内力です。

　したがって、AとBからなる系には運動量保存則が成り立って、
それを表す式は、
\begin{equation} mv'+MV'=mv+M\times 0 \tag{4-10} \end{equation}
です。　これより、
\begin{equation} v'=v-\frac{M}{m}V' \tag{4-11} \end{equation}
となります。

【運動方程式を用いる】

　運動方程式をつかっても解けます。
A,Bそれぞれの貫通途中の加速度を\(a_1,a_2\)として、
水平方向の運動方程式を立てると、
\begin{eqnarray} A&：& ma_1=-f \tag{4-12} \\
B&& Ma_2=f \tag{4-13} \end{eqnarray}
となります。
　したがって、\(a_1=-\frac{f}{m}、a_2=\frac{f}{M}\)　です。

貫通に要する時間を\(t\)とします。貫通直後のA,Bそれぞれの速度は、\(v'、V'\)ですから、
\begin{eqnarray} v'&=&v+a_1t 　\tag{4-13} \\
V'&=&a_2t \tag{4-14}
\end{eqnarray}
（4-14）式から \(t\)を求め、（4-13）式に代入すれば、
\begin{equation} v'=v-\frac{M}{m}V' \tag{4-15} \end{equation}
となります。

【運動エネルギーと仕事の関係」を用いる】

　球Aと物体Bにはたらく水平方向の力は\(f\)だけです。
重力は鉛直方向にしかはたらかないので、速度の水平方向成分には影響を与えません。

　さて、AがBに接触してから、貫通した直後まで、\(f\)がAにする仕事を求めます。
\(f\)とAの運動の向きは逆向きですから、\(f\)がAにした仕事は負です。
移動距離は、図4-2（ｃ）がからわかるように、\(L+l\)です。
\(l\)ではないことに注意しましょう。
Bに対してAが相対的に移動した距離は\(l\)ですが、
仕事を求めるときには、床に対して移動した距離を用います。
以上より、求める仕事は、\(-f(L+l)\)です。

　一方、\(f\)がBにする仕事は、\(fL\)です。

　以上より、「運動エネルギーと仕事の関係」を表す式は、
\begin{eqnarray} A&：& \frac{1}{2}mv'^2-\frac{1}{2}mv^2=-f(L+l) \tag{4-16} \\
B&：& \frac{1}{2}MV'^2-\frac{1}{2}M\times 0^2=fL \tag{4-17}
\end{eqnarray}
となります。

　ここで、（4-16）式+（4-17）式を計算すると、
\begin{eqnarray} (\frac{1}{2}mv'^2+\frac{1}{2}MV'^2)-(\frac{1}{2}mv^2+\frac{1}{2}M\times 0^2)=-fl \tag{4-18} \end{eqnarray}
と、なります。
　これは、[距離L移動後のAとBの運動エネルギーの和]+[初期のAとBの運動エネルギーの和]=\(-ｆｌ\)
と解釈できます。

　結局、例1と異なり、「運動エネルギーと仕事の関係」からは答えが得られないようです。
それは、AとBで逆向きで大きさが同じ力を受けながら、AとBの移動距離が異なるため、（4-16）（4-17）式から\(L\)と\(l\)の両方を消去することができないからです。

物理の大学入試問題を解く