Ⅰ.p-Vグラフの基本-状態方程式
ここでは、p-Vグラフの基礎について説明します。
p-Vグラフ上の点は気体のひとつの状態を表しています。
理想気体の状態を理解するには、理想気体の状態方程式を使います。
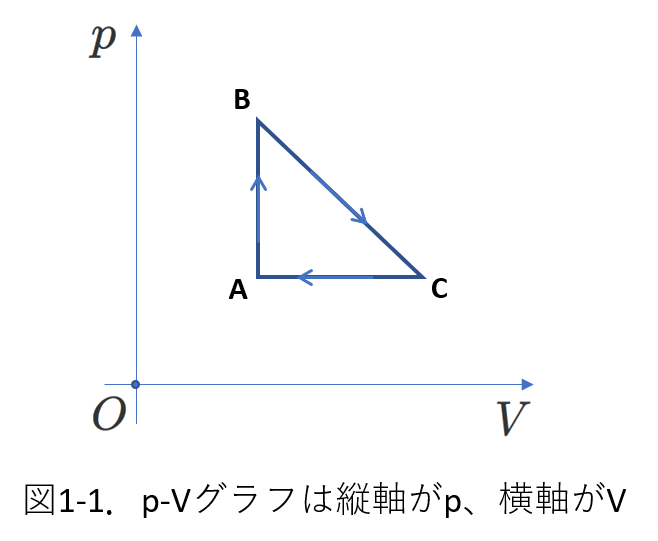
p-Vグラフは、図1-1のように、縦軸が\(p\)(圧力)、横軸が\(V\)(体積)です。
グラフの名称は、「縦軸の名称」-「横軸の名称」グラフと呼ぶのが普通です。
これをうっかり逆にした図(縦軸が\(V\)、横軸が\(p\))を描いてしまうことがあるので、注意しましょう。
さて、図1-1のp-Vグラフ上に、ひとつの点を取ります。 例えば、\(A\)です。
点\(A\)は気体のひとつの状態を表しています。
気体の状態は、圧力・体積・絶対温度・モル数で表されます。
また、高校の学習課程では、気体として理想気体を扱います。
それも、特に単原子分子理想気体という条件で出題されることが多いです。
したがって、以下の記事でも主に単原子分子理想気体を扱います。
1.状態方程式で気体の状態を理解する
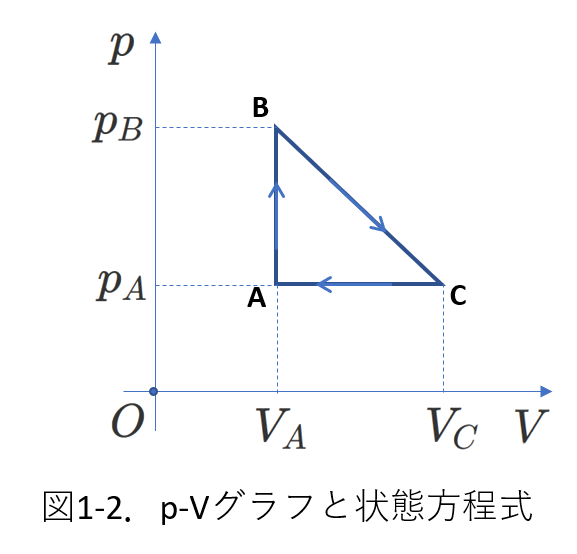
図1-2を見てください。
このグラフは、状態\(A\)にある気体の圧力が\(p_A\)、体積が\(V_A\)であることを示しています。
気体の圧力と体積がわかれば、状態方程式から、気体の絶対温度もわかります。
ただし、モル数をグラフから読み取ることはできません。
モル数は普通、問題で与えられます。
ここで覚えておきたいことは、p-Vグラフ上に、圧力\(p\)と体積\(V\)が示されていれば、絶対温度\(T\)もわかるということ、つまり、p-Vグラフ上に状態を表す点が示されていれば、その気体について、圧力\(p\)、体積\(V\)、絶対温度\(T\)がわかるということです。
p-Vグラフに関連して使用される公式は、次に示す「理想気体の状態方程式(1-1)式」と「熱力学の第一法則(1-2)式」です。
\begin{eqnarray} pV&=&nRT \tag{1-1} \\
Q&=&\Delta U+W \tag{1-2} \\
\end{eqnarray}
ここで、 \(Q\):気体に入る熱量
\(\Delta U\):内部エネルギーの変化量
\(W\):気体が外部にする仕事
です。
状態方程式 \(pV=nRT\) によれば、p-Vグラフ上の点が決まれば(\(p、V\)の値がわかれば)\(T\)も求まることがわかります。
上2式のうち、熱力学の第一法則については、次からの章で詳しく説明することにして、ここでは、主に状態方程式について説明します。
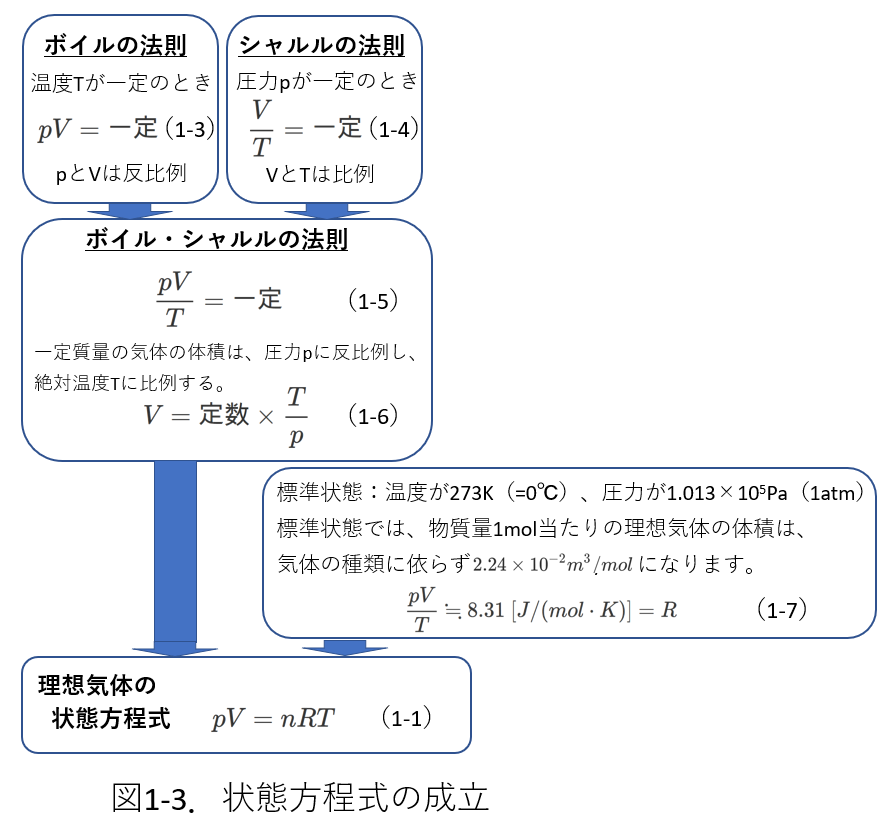
ここで、理想気体の状態方程式\(pV=nRT\)はどのように導かれたかを確認しておきましょう。
図1-3にそれをまとめました。
ボイルの法則 \(pV=一定 \tag{1-3} \)とシャルルの法則 \(\frac{V}{T}=一定 \tag{1-4} \)
をひとつの式にまとめたものが、ボイル・シャルルの法則
\begin{equation} \frac{pV}{T}=一定 \tag{1-5} \end{equation}
です。
また、温度が\(273K(=0℃)\)、圧力が\(1.013×10^5Pa(=1atm)\)である状態を標準状態といいます。
標準状態では、物質量\(1\)モル当たりの理想気体の体積は、気体の種類に依らず\(2.24×10^{-2}m^3\)になります。
これらの値で\(\frac{pV}{T}\)を計算すると、\(n=1\)モルのときの \(\frac{pV}{T}=R\) の式の気体定数\(R\)の値\(8.31J/(mol・K)\)が求められます。
以上を、\(n\)モルのときに拡張すれば(1-1)式が導かれます。
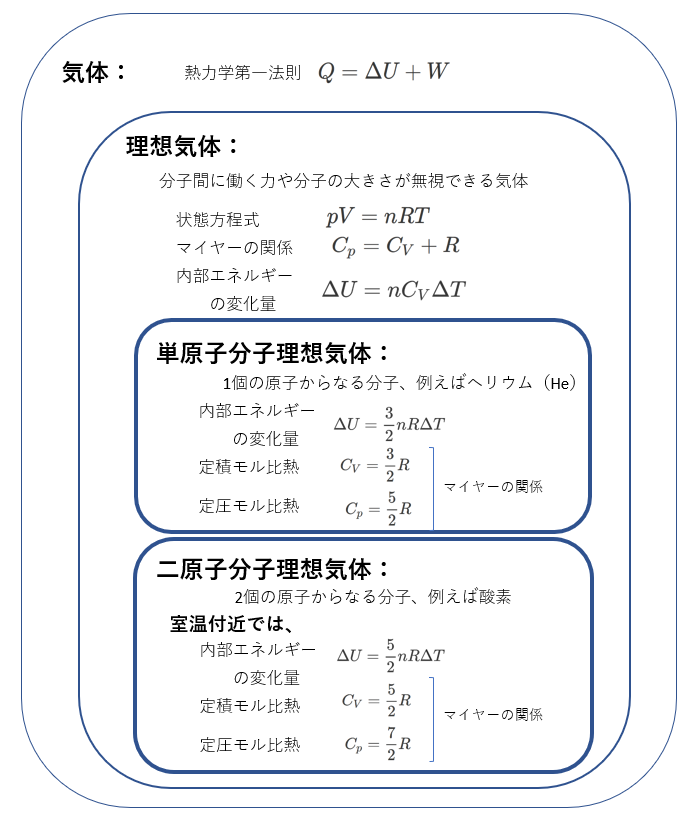
高校の物理で扱う気体は、単原子分子理想気体が多いです。
公式と気体の種類とは関係があるので、その関係も一緒に理解する必要があります。
その関係を次の表に示します。
二原子分子理想気体の内部エネルギーとモル比熱については、教科書にも記述があるようです。
二原子分子では、重心の3方向への並進運動以外に、2つの軸の周りの回転運動が内部エネルギーに関与するようになります。
上表に、「室温付近では」との断り書きがあるのは、温度がさらに上昇すると、原子間の振動運動も加わり、モル比熱はさらに大きくなるからです。
問題文中に、「単原子分子理想気体」と書いてあれば、気体の内部エネルギーは\(\frac{3}{2}nRT\)でいいのですが、単に「理想気体」と書かれている場合もありますから、問題文をしっかり読んでどういう気体なのかを確認する必要があります。
単なる「理想気体」であれば、内部エネルギーの変化として\(\frac{3}{2}nR\Delta T\)を使うことはできません。 この場合、定積モル比熱\(C_V\)が与えられていることが多くて、\(nC_V\Delta T\)を用います。
2.状態方程式で気体の状態変化を理解する
状態方程式は、圧力\(p\)と体積\(V\)と絶対温度\(T\)の関係を示しています。
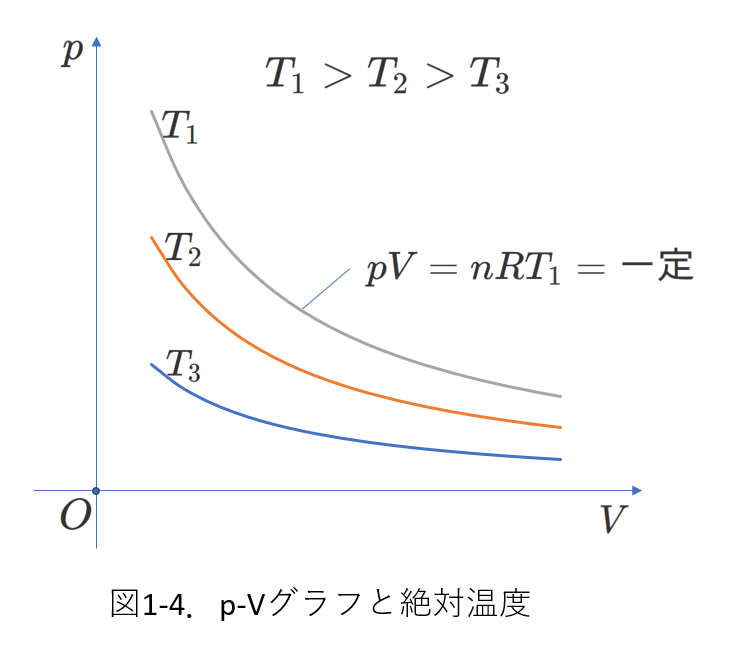
状態方程式に依れば、絶対温度が一定という条件での\(p\)と\(V\)の関係は、図1-4のように直角双曲線となります。
これは、状態方程式 \(pV=nRT\) において、\(T=一定\)ならば、\(p=\frac{一定値}{V}\)と表せることからわかります。
(ボイルの法則、以後、この直角双曲線を等温線と呼びます。)
図1-4には、\(T_1\gt T_2\gt T_3\)の3つの絶対温度で\(p\)と\(V\)の関係を示すグラフが描かれています。
状態方程式からわかるように、等温線のグラフは、上のもの(\(p\)が大きい)ほど、あるいは、右のもの(\(V\)が大きい)ほど、絶対温度が高いです。
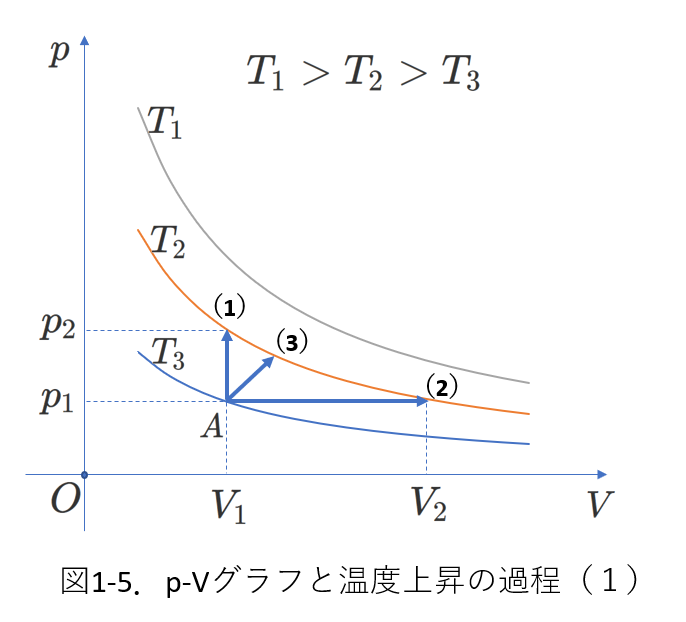
右図1-5で、点\(A\)(絶対温度\(T_3\)、圧力\(p_1\)、体積\(V_1\))から、(1)(2)(3)への過程を考えます。
このうち、\(A\to (1)\) は定積過程、
\(A\to (2)\) は定圧過程
です。
これら3つの過程ではいずれも、絶対温度が \(T_3\) から \(T_2\) に増加します。
これは、内部エネルギーが、\(\frac{3}{2}nRT_3\) から \(\frac{3}{2}nRT_2\) に増加したと捉えることもできます。(単原子分子理想気体の場合、内部エネルギーは\(\frac{3}{2}nRT\)と表されます)
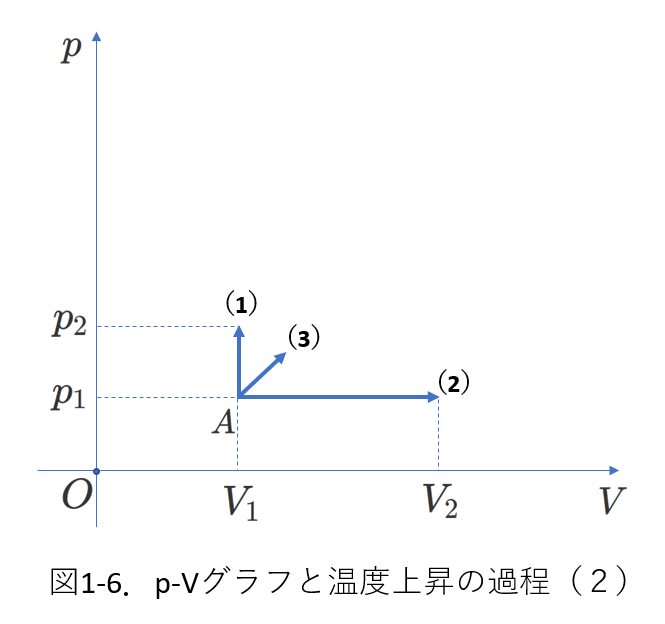
図1-5を見れば、等温線が示されているので絶対温度が増加していることは明らかですが、図1-6のように等温線が示されていない場合でも絶対温度が増加していると捉えることができると良いです。
状態が、図1-6のように、\(A\)から\((1)、(2)、(3)\)への変化をしたら、絶対温度、および、その内部エネルギーが増加していると判断しましょう。
それを意識すると、\(p-V\)グラフの理解が楽になります。
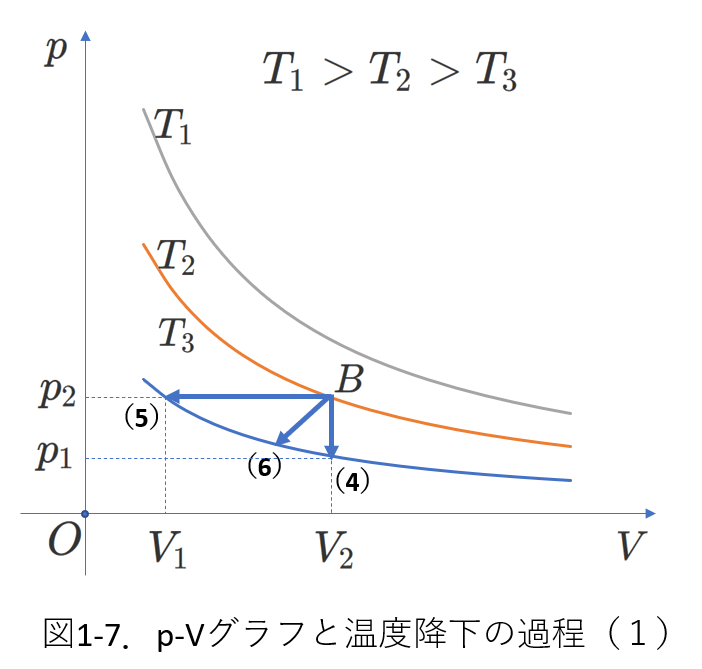
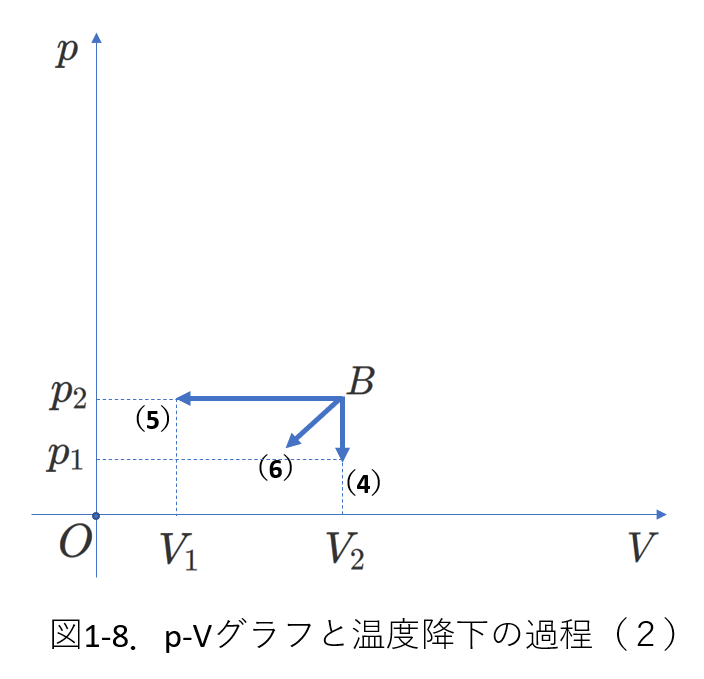
図1-5の反対の過程を図1-7に示します。
点\(B\)から\((4)、(5)、(6)\)への変化過程です。
絶対温度が \(T_2\) から \(T_3\) へ減少します。
これは、内部エネルギーが \(\frac{3}{2}nRT_2\) から \(\frac{3}{2}nRT_3\) へ減少すると捉えることもできます。(単原子分子理想気体の場合)
等温線を省いた図1-8でも、これらの過程では、絶対温度、および、内部エネルギーが減少すると、読み取れるようにしておきましょう。
3.例題
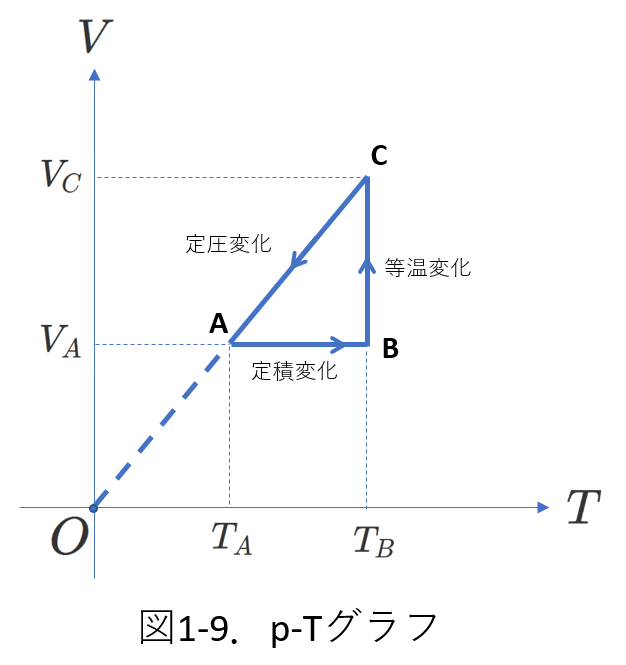
1molの単原子分子理想気体の状態を、右図1-9に示すように\(A\to B\to C\to A\)と変化させます。
この図1-9は縦軸\(V\)、横軸\(T\)の\(V-T\)グラフですが、これを\(p-V\)グラフに書き直します。
状態\(A、B、C\)はそれぞれ体積と絶対温度がわかっているので、状態方程式を使って圧力を計算し、\(p-V\)グラフを描きます。
状態\(A\)については、体積\(V_A\)、絶対温度\(T_A\)、物質量\(1mol\)ですから、圧力を\(p_A\)として、状態方程式は、
\begin{eqnarray} p_AV_A&=&RT_A \\
これより、p_A&=&\frac{RT_A}{V_A} \tag{1-8} \end{eqnarray} が得られます。
同様に考えれば、
\begin{eqnarray} p_B&=&\frac{RT_B}{V_A} \tag{1-9} \\
p_C&=&\frac{RT_B}{V_C} \tag{1-10}
\end{eqnarray}
です。
状態変化について考えると、\(A\to B\)は定積変化、\(B\to C\)は等温変化です。
\(C\to A\)では、線分\(CA\)を延長した直線が原点\(O\)を通りますから、体積\(V\)は温度\(T\)に比例します。
すなわち、、過程\(C\to A\)は、定圧変化です。
定圧変化であることは、シャルルの法則から判断できます。
また、比例定数を\(C\)とすれば\(V=CT\)と表すことができて、
体積\(V\)は状態方程式から\(V=\frac{R}{p}T\)ですから、\(C=\frac{R}{p}\)、すなわち\(p=\frac{R}{C}=一定\)となり、定圧変化であることを示せます。
つまり、\(p_A=p_C\)です。
(1-8)式と(1-10)式からだけでは\(p_A=p_C\)はわかりません。
過程\(C\to A\)が原点を通る直線であることに気付いて初めて\(p_A=p_C\)を導くことができます。
状態ともうひとつの状態を結ぶ直線あるいは曲線からわかることもあることを覚えておきましょう。
そこで、\(p-V\)グラフを描くと、右図1-10のようになります。
図1-9のグラフでは、状態の変化が左回り、図1-10では右回りになっていることを確認しておきましょう。
状態\(A、B\)の圧力は(1-8)(1-9)式を用いて示すのが普通ですが、ここでは単に\(p_A、p_B\)と表すことにします。
過程\(A\to B\)は定積変化です。
過程\(B\to C\)は、図1-9から等温変化とわかります。
等温変化は\(p-V\)グラフでは直角双曲線になります。(図1-4を参照)
状態\(B\)と\(C\)を直線で結んでしまうようなことがないように注意しましょう。
ところで、[圧力]、[体積]、[温度]の3つの変数があるので、グラフは3種類(縦軸・横軸の違いまで数えれば6種類)考えられます。
残りは、p-Tグラフです。
これを図1-11に示します。
ここで注意するのは、定積変化の\(A\to B\)の過程です。
状態方程式を書き直すと、
\begin{eqnarray} p=\frac{R}{V}T \end{eqnarray}
ですから、体積\(V\)が一定の場合には、\(p\)と\(T\)は比例関係にあります。
つまり、\(A\to B\)の過程は線分で結ばれ、これを延長すれば、原点\(O\)を通ります。
図1-11の\(A\to B\)の過程の線分を描く場合には、原点\(O\)を貫くことがわかるように注意して描きましょう。
Ⅱ.p-Vグラフの基本-熱力学第一法則 Ⅰ
1.熱力学第一法則
「熱と気体」で使われる主な式は次の4つです。
\begin{eqnarray} pV&=&nRT (理想気体)\tag{2-1} \\
Q&=&\Delta U+W \tag{2-2} \\
\Delta U&=&\frac{3}{2}nR\Delta T (単原子分子理想気体) \tag{2-3} \\
W&=&p\Delta V \tag{2-4} \\
\\
ここで、 Q&:&気体に入る熱量 \\
\Delta U&:&内部エネルギーの変化量 \\
W&:&気体が外部にする仕事 \\
\Delta V&:&体積変化 \\
を表します。
\end{eqnarray}
(2-1)式は理想気体のときに成り立つ状態方程式で、
(2-3)式は単原子分子理想気体の時に成り立つ内部エネルギーの式です。
気体分子は相互に力を及ぼし合っています。
この力は保存力で、気体分子はこの力による位置エネルギーを持っています。
同時に、気体分子は熱運動による運動エネルギーも持っています。
位置エネルギーと運動エネルギーをすべての分子について合計したものが気体の内部エネルギーです。
理想気体では分子間の力、すなわち、位置エネギーを無視して、考えます。
また、単原子分子理想気体では、運動エネルギーとして分子の並進運動だけを考え、回転エネルギー等を考慮しません。
(2-3)式はそのような仮定で計算して得られた式で、単原子分子理想気体に対して成り立つ式です。
内部エネルギーの式の導出過程は色々に変形されて出題されることがあるので、教科書での説明をしっかり理解しておきましょう。
「熱と気体」の分野の解答で多いのは、符号ミスです。
熱力学第一法則を表す(2-2)式でも、符号ミスをすることがあります。
(2-2)式の各項の符号は、\(Q、W\)をどのように定義するかによって変わるからです。
(2-2)式では、\(Q\)を「気体に入る熱量」と定義しています。
しかし、問題によっては、「気体が吸収する熱量」とか、「気体から出る熱量」とか「気体が放出する熱量」と表されている場合があります。
「気体が放出する熱量」=-「気体に入る熱量」ですから、\(Q'\)を「気体が放出する熱量」とすれば、(2-2)式は、
\begin{equation} -Q'=\Delta U+W \tag{2-5} \end{equation}
となります。
次に、(2-2)式では、、\(W\)は「気体が(外部に)した仕事」です。
これに関連する表現で、「気体が(外部から)された仕事」、「気体が受けた仕事」、「外部気体が受けた仕事」などがあります。
表現は色々あるので、内容を十分に吟味する必要があります。
「気体が外部にした仕事」=-「気体が(外部から)された仕事」
であることに注意しましょう。
以上のことから、「熱量」「仕事」とだけ捉えるのではなく、「出る熱量」なのか「入る熱量」なのか、「する仕事」なのか「される仕事」なのかを強く意識することが大事だとわかります。
また、問題にない文字を自分で定義して使う場合、\(Q\)についてなら、「出る熱量」なのか「入る熱量」なのかを説明しておきましょう。 採点者の混乱をさけるためと、自分の勘違いによる符号ミスを防ぐためです。
今、解いている問題を中断して別の問題を解き、戻って解き続ける場合、
\(Q\)が「出る熱量」なのか「入る熱量」なのかがメモしてあれば、スムーズに戻ることができます。
また、見直しも楽にできます。
\(\Delta U\)は内部エネルギーの変化量です。
\begin{equation} \Delta U=[変化後の内部エネルギー」-[変化前の内部エネルギー] \tag{2-6} \end{equation}
です。
[変化量]は、
\begin{equation} [変化量]=[変化後の値」-[変化前の値] \tag{2-7} \end{equation}
に決まっていて、引く順序を変えてはいけません。
関連する言葉に、[増加量]、[減少量]があります。
\begin{eqnarray} &&[変化量]=[増加量]=-[減少量] \tag{2-8} \\
&&[減少量]=[変化前の値]-[変化後の値] \end{eqnarray}
を覚えておきましょう。
問題によっては、[内部エネルギーの減少量]を答えるものがあり、(2-8)式にしたがって、符号ミスがないように答えましょう。
さて、\(Q、\Delta U、W\)のうち、\(\Delta U\)はほかのふたつと性格が異なります。
それは、\(Q\)、および、\(W\)の出入りの結果が\(\Delta U\)であるという捉えかたができる点です。
したがって、(2-2)式を書き換えて、
\begin{equation} \Delta U=Q-W \tag{2-9} \end{equation}
とした方が理解しやすいようです。
(2-9)式は次のように理解できます。
気体に\(Q\)の熱量が入れば(つまり、\(Q\)の符号が正ならば)、入った熱量は内部エネルギー\(\Delta U\)を増加させます。
外部にする仕事\(W\)が増えれば(つまり、\(W\)の符号が正ならば)、内部エネルギーを使って外部に仕事をするわけですから、\(\Delta U\)は減少します。
熱力学第一法則の式を立てたときに、このように考えることで、\(Q\)と\(W\)の符号のチェックができます。
それでは、問題です。
熱力学第一法則が次のように書かれていたら、\(Q''\)、\(W''\)は何を表すかを考えてみましょう。
\begin{equation} \Delta U=-Q''+W'' \tag{2-10} \end{equation}
\(Q''\)があると\(\Delta U\)が減るのですから、\(Q''\)は「気体が放出する熱量」です。
\(W''\)があると\(\Delta U\)が増えるのですから、\(W''\)は「気体が外部からされる仕事」です。
熱力学第一法則は、エネルギーの収支の式です。
つまり、熱量と仕事の出入りの量に応じて、気体の内部エネルギーが増減します。
まとめると、
状態方程式は、圧力、体積、絶対温度の間の関係を規定していて、大雑把に言えば、\(p-V\)グラフ上でひとつの点を調べるときに用います。 また、同時に、状態方程式は、(等温変化のときに、\(p-V\)グラフが直角双曲線になることを教えてくれるように)、状態から別の状態へ変化する経路を教えてくれる場合があります。
これに対して、熱力学の第一法則は、状態から別の状態へ変化したときのエネルギーの収支を調べるのに用います。
2.\(p-V\)グラフと仕事
【力学】では、[仕事の大きさ]は [力の大きさ]×[移動距離] で表されていました。
【熱と気体】の分野では、[力]よりも[圧力]を用いるので、仕事も[圧力]で表されることが多いです。
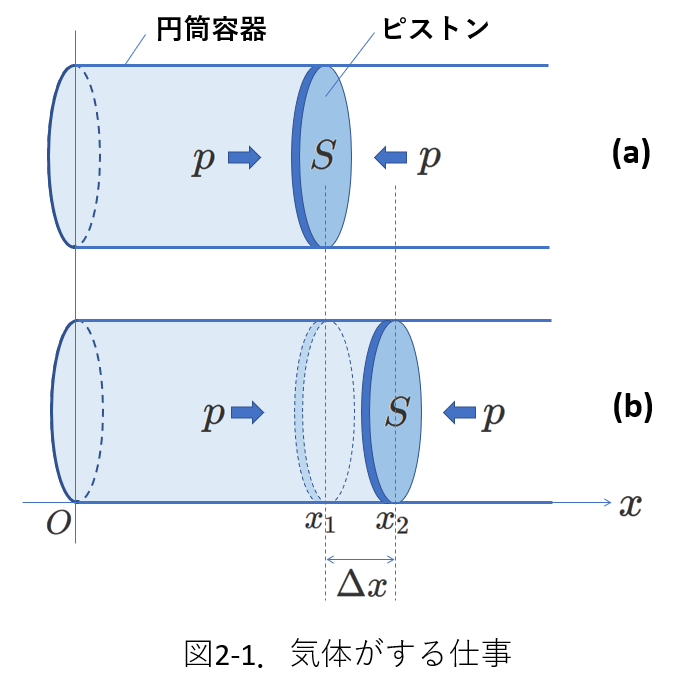
右図2-1のように、ピストンが自由に動くことができる円筒容器を考えます。
円筒容器とピストンに囲まれる空間には、単原子分子理想気体(以後、気体と呼びます)が入っています。
円筒容器および、ピストンは熱を伝えない材質でできています。
ピストンの面積は\(S\)です。
円筒容器の底(左端)を原点として容器に沿って右向きの\(x\)軸を考えます。
図2-1(a)では、ピストンが\(x=x_1\)の位置で静止しています。
この状態では、気体の圧力\(p\)と外部気体の圧力がつりあっています。
(a)の状態で、気体に熱量を加えます。
気体は熱量を受けて圧力が上りますが、ピストンは自由に動くので、気体の圧力と外部気体の圧力が大きさ\(p\)で、つり合った状態のままピストンが右に動きます。
つまり、気体は膨張します。
そして、\(x=x_2\)までピストンが動いたとします。
このとき、気体のした仕事\(W\)は、
\begin{eqnarray} W&=&[力]\times [移動距離] \\
&=&[圧力:p]\times [断面積:S]\times (x_2-x_1) \\
&=&pS(x_2-x_1) \\
&=&p(Sx_2-Sx_1) \tag{2-11} \\
&=&p(V_2-V_1) \tag{2-12} \\
&=&p\Delta V \tag{2-13} \\
ここで、V_2&=&Sx_2、V_1=Sx_1、\Delta V=V_2-V_1
\end{eqnarray}
と表されます。
(2-13)式は、\(W=p\Delta V\) であって、\(V\Delta p\) ではないことを確認してください。
両者ではまったく意味が違います。
間違って縦軸\(V\)、横軸\(p\)のグラフを描いて、グラフと横軸との間の面積を求めてしまうと、\(V\Delta p\)を求めたことになるので、注意しましょう。
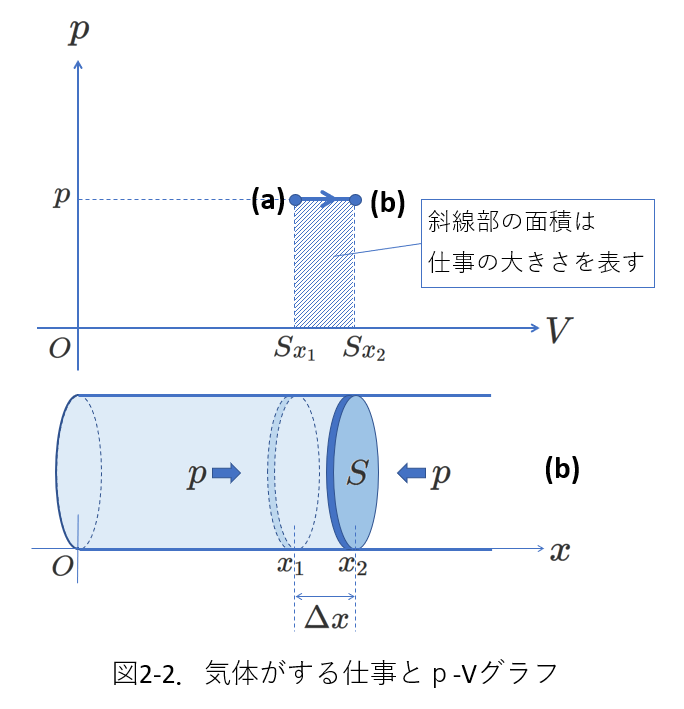
さて、(2-13)式と\(p-V\)グラフの関係を図2-2に示します。
(2-11)~(2-13)式から、\(W\)は図2-2の\(p-V\)グラフの斜線部の面積に等しいことがわかります。
面積は常に正の値ですから、面積が表すのは[仕事の大きさ]です。
そして、[仕事]の「正負」は、気体が膨張するか、収縮するかで決まります。
\(W\)を「気体がした仕事」とすれば、気体が膨張していれば、「気体が外部に仕事をした」として\(W\)は正、気体が収縮していれば、「気体は外部から仕事をされた」として\(W\)は負となります。
なお、
\begin{eqnarray} \Delta V&=&[気体の体積変化] \\
&=&[変化後の気体の体積]-[変化前の気体の体積]
\end{eqnarray}
として、[気体がした仕事]を計算すれば、[仕事]の正負も含めて正しく計算できます。
図2-2の過程は定圧変化で、\(p=一定\)ですから、\(p\Delta V\) が計算しやすいです。
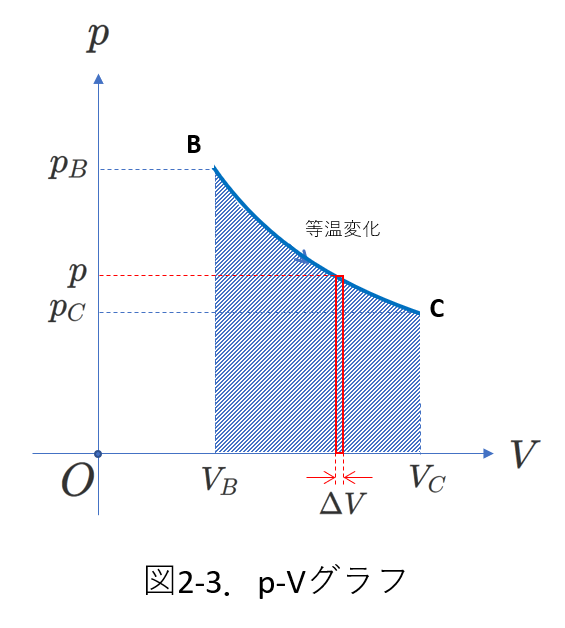
次に、右図2-3の過程\(B\to C\)が等温変化の場合を例にして、\(p\)が一定でない場合の[仕事]の求め方を考えます。
図のように、圧力が\(p\)のときに、圧力が一定と見なせるぐらい小さな体積変化\(\Delta V\)を考えると、この変化での[仕事の大きさ]は\(p\Delta V\)です。この微小区間を\(V_B\)から\(V_C\)まで足せばいいのですから、これは\(p\)を\(V_B\)から\(V_C\)まで積分することになります。
つまり、\(p\)がどのように変化していても(していなくても)、[気体がした仕事]は\(p-V\)グラフと\(V\)軸との間の面積に対応します。
そこで、求める[仕事]を\(W'\)として、
\begin{eqnarray} |W'|&=&\int_{V_B}^{V_C} pdV \tag{2-14} \\
等温変化ですから、C\ \left(=nRT\right)を定数として、p&=&\frac{C}{V} \ と表されるので、 \\
|W'|&=&\int_{V_B}^{V_C} \frac{C}{V}dV \tag{2-15} \\
&=&C\int_{V_B}^{V_C} V^{-1}dV \\
&=&C[\ln V]_{V_B}^{V_C}=C(\ln V_C-\ln V_B)=C\ln{\frac{V_C}{V_B}}
\end{eqnarray}
となります。
高校の物理ではこの積分までは求められないと思いますが、高校数学でこの積分はできますね。
\(B\to C\)の過程で体積は増加(膨張)しますから、仕事\(W'\gt 0\) です。
さて、気体のした仕事\(W=p\Delta V\)はどこにいくのかを考えます。
ポイントは、ピストンにはたらく気体の圧力\(p\)と外部気体の圧力\(p\)とが釣り合っているので、ピストンが\(x_1\)から\(x_2\)へ移動したとき、ピストンの運動エネルギーは変化しないことです。
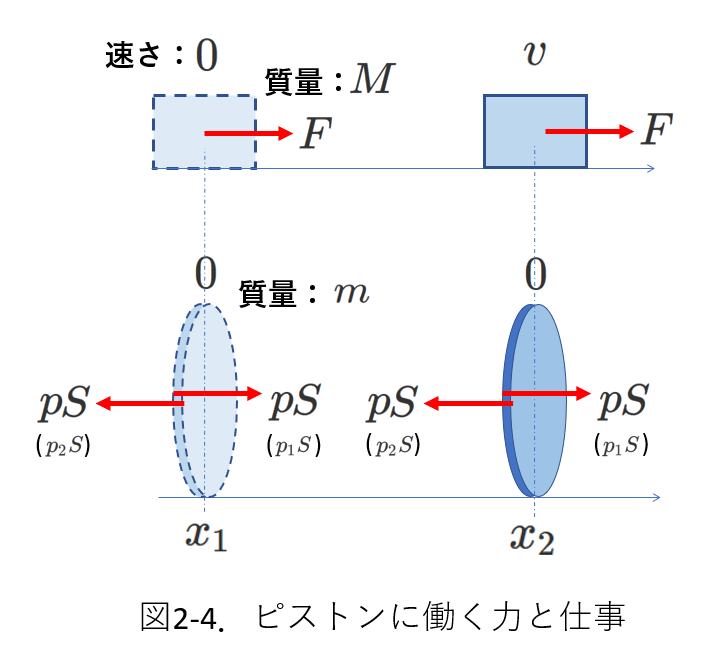
図2-4を見てください。
上の段は、質量\(M\)の静止している物体に\(F\)力を加え続けて、\(x_1\)から\(x_2\)に移動させたとき、速さが\(v\)になったことを示しています。
\(F\)のした仕事は\(F(x_2-x_1)\)で、運動量変化との関係を表す式は次のようになります。
\begin{equation} \frac{1}{2}Mv^2-\frac{1}{2}M\times 0^2=F(x_2-x_1) \tag{2-16} \end{equation}
一方、図2-1の状況を、図2-4の下段に示しましたが、
ピストンには、気体の圧力による力と、外部気体の圧力による力の両方が加わっていて、このふたつの力がする仕事によるピストンの運動エネルギーの変化量は\(0\)(つまり、変化しない)です。
ふたつの力の大きさは同じですが、気体の圧力を\(p_1\)、外部気体の圧力を\(p_2\)と表すことにします。
(2-16)式と同じ形式で式に表すと、
\begin{eqnarray} \frac{1}{2}m\times 0^2-\frac{1}{2}m\times 0^2&=&p_1 S(x_2-x_1)-p_2 S(x_2-x_1) \tag{2-17} \\
これより、p_1 S(x_2-x_1)&=&p_2 S(x_2-x_1) \tag{2-18}
\end{eqnarray}
ここで、外部の気体がピストンにした仕事は、\(-p_2 S(x_2-x_1)\)です。
ピストンの動きと、外部気体がピストンに及ぼす力は逆向きなので負号をつけています。
外部気体がピストンに\(-p_2 S(x_2-x_1)\)の仕事をしたということは、外部気体は\(p_2 S(x_2-x_1)\)の仕事を気体から受け取ったことになります。
これは、気体が外部にした仕事\(p_1 S(x_2-x_1)\)と同じ大きさですから、気体は外部気体に対して仕事をして、外部気体が同じ量の仕事をエネルギーとして受け取ったと解釈できます。
3.例題
「円筒容器内の気体がした仕事はどうなるか」に関連した問題を3つ取り上げます。
ただし、これらの問題は、\(p-V\)グラフに直接には関係ありません。
3-1.Aの気体がした仕事を、Bの気体が受け取る例
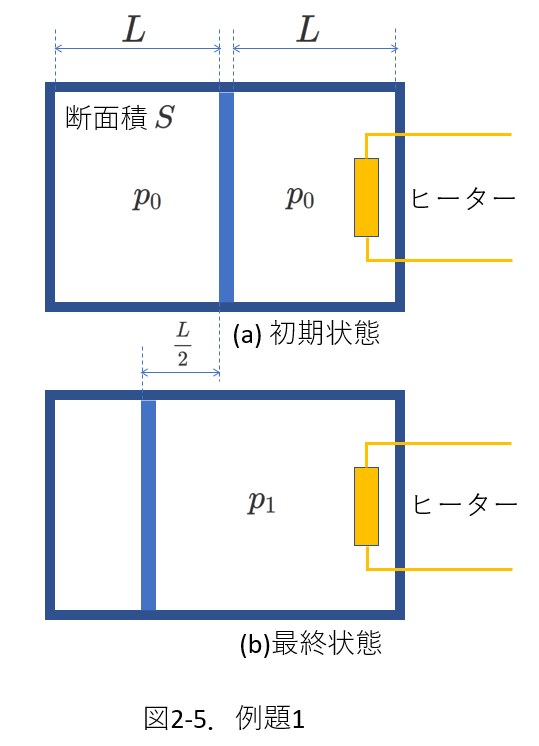
図2-5のように、両側が密閉された円筒形のシリンダーがあって、その内部空間を、シリンダーに対して自由に動くことのできるピストンが二つの部屋に分けています。
シリンダーもピストンも断熱材でつくられていて、壁を通して熱が出入りすることはありません。
また、どちらの部屋にも、内部には単原子分子理想気体が満たされています。
今、(a)のように、ふたつの部屋の長さがそれぞれ\(L\)で、各部屋の圧力はいずれも\(p_0\)です。
シリンダーの断面積は\(S\)です。
右の部屋にだけヒーターがあって、徐々に加熱したところピストンがゆっくり動き、(b)に示したように、最初の位置から\(\frac{1}{2}L\)離れた位置でピストンが静止し、、右側の部屋の気体の圧力が\(p_1\)となりました。
このとき、ヒーターが右の部屋に与えた熱量を求めます。
熱量を直接もとめることはできませんから、熱力学の第一法則を利用します。
熱力学第一法則によれば、熱量を求めるには、気体の内部エネルギーの変化量と気体がした仕事を求めることになります。
しかし、気体がした仕事を求めるのは難しそうです。
それは、動いた距離、つまり、体積変化はわかるのですが、圧力が\(p_0\)から\(p_1\)に変化している(圧力が一定ではない)ので、単純な\(p\Delta V\)という式が使えないからです。
では、内部エネルギーの変化は求められるでしょうか。
内部エネルギーを求めるには、温度\(T\)がわかっているか、圧力\(p\)と体積\(V\)の両方がわかっていることが、必要です。
(a)の状態は、左側の部屋も右側の部屋も、圧力と体積がわかっているので、内部エネルギーを求めることができます。
(b)では、左側の部屋の圧力が書かれていませんが、ピストンは自由に動けること、(b)の状態でピストンは静止していることから、左右の部屋の圧力がつりあっていることがわかって、左側の部屋の圧力は\(p_1\)であると、わかります。
したがって、内部エネルギーを求めることができます。
現象を確認しておくと、
ヒータを加熱すると、右側の部屋の温度が上がり、圧力が上昇します。
このため、ピストンが徐々に左に動き、左の部屋の圧力を高めます。
この圧力が右側の部屋の圧力と同じになればピストンの移動は止まりますが、ヒータの過熱を続ければ、ピストンはゆっくり動き続けます。
では、熱力学の第一法則の式を立てます。
重要なことは、右側の部屋と左側の部屋それぞれについて熱力学第一法則の式を立てることです。
右側の部屋について、わかっていない量を、仮の文字で表します。
加える熱を\(Q\)、右の部屋の気体がする仕事を\(W_1\)とすれば、
\begin{eqnarray} Q&=&\Delta U_1+W_1 \tag{2-19} \\
&=&\frac{3}{2}\left(p_1S(L+\frac{1}{2}L)-p_0SL\right)+W_1 \\
&=&\frac{9}{4}p_1SL-\frac{3}{2}p_0SL+W_1 \tag{2-20} \end{eqnarray}
左側の部屋について、注意するのは、熱の出入りがないことです。
したがって、左側の部屋の気体がする仕事を\(W_2\)とすれば、熱力学第一法則は、
\begin{eqnarray} 0&=&\Delta U_2+W_2 \tag{2-21} \\
&=&\frac{3}{2}\left(p_1S(L-\frac{1}{2}L)-p_0SL\right)+W_2 \\
&=&\frac{3}{4}p_1SL-\frac{3}{2}p_0SL+W_2 \tag{2-22} \end{eqnarray}
\(\Delta U_1\)と\(\Delta U_2\)はそれぞれの部屋の内部エネルギー変化を表しています。
単原子分子理想気体の場合、内部エネルギーは\(\frac{3}{2}nRT\)で表されますが、これは、\(\frac{3}{2}pV\)と表すことができます。
本問では、絶対温度ではなく圧力と体積が与えられているので、後者の式を使うほうが計算が楽です。
(解法の途中ですが)、まとめておくと、
初期状態の、圧力が\(p_1\)、体積が\(V_1\)、絶対温度が\(T_1\)のとき、内部エネルギー\(U_1\)は、
\begin{eqnarray} U_1&=&\frac{3}{2}nRT_1 \\
&=&\frac{3}{2}p_1V_1 \tag{2-23} \end{eqnarray}
最終状態の、圧力が\(p_2\)、体積が\(V_2\)、絶対温度が\(T_2\)のとき、内部エネルギーの変化量\(\Delta U\)は、
\begin{eqnarray} \Delta U&=&\frac{3}{2}nR(T_2-T_1)=\frac{3}{2}nR\Delta T \\
&=&\frac{3}{2}\left(p_2V_2-p_1V_1\right)=\frac{3}{2}\Delta (pV) \tag{2-24} \\
ここで、\Delta (pV)&=&p_2V_2-p_1V_1=(p_1+\Delta p)(V_1+\Delta V)-p_1V_1=p_1\Delta V+\Delta p\cdot V_1+\Delta p\cdot \Delta V
\end{eqnarray}
です。
(2-24)式の右辺は、\(p\Delta V\)でも\(\Delta p\cdot V\)でもないことに注意してください。
( (2-23)(2-24)式の、それぞれひとつ上の式に状態方程式を適用すれば直ちに(2-23)(2-24)式が得られます。)
さて、問題に戻って、\(W_1\)について考察します。
右側の気体は明らかに左側の部屋の気体に対して仕事をしています。
そして、ピストンの運動エネルギーが変化していないので、[右側の気体がした仕事]がピストンの[運動エネルギーの増加]に使われたということもありません。
また、左側の部屋の気体の体積は減少していますから、左側の部屋の気体は、仕事をされたということになります。
以上より、
[右の部屋の気体がした仕事]=[左側の部屋の気体がされた仕事]=-[左側の部屋の気体がした仕事]
であることがわかります。
つまり、\(W_1=-W_2\) (2-25) です。
(2-20)式と(2-22)式の各辺ごとの和を取ると、
\begin{eqnarray} Q+0&=&\left(\frac{9}{4}+\frac{3}{4}\right) p_1SL+\left(-\frac{3}{2}-\frac{3}{2}\right) p_0SL+W_1+W_2 \\
Q&=&3SL\ (p_1-p_0) \tag{2-26} \end{eqnarray}
となりました。
ところで、この問題で、\(p_1\)、および、\(W_1\)を求めることはできるのでしょうか?
言い換えれば、\(p_1\)と\(W_1\)を、\(S、L、p_0\)を使って表すことができるでしょうか?
断熱変化では、圧力\(p\)と体積\(V\)の間に、
\begin{eqnarray} pV^\gamma&=&一定 \\
ここで、\gamma&=&\frac{定圧モル比熱}{定積モル比熱} \\
&=&\frac{5}{3} (単原子分子理想気体の場合)
\end{eqnarray}
という関係があります。
左側の部屋は断熱変化をするので、上の式が使えます。
最初の状態では、圧力が\(p_0\)、体積が\(SL\)
最後の状態では、圧力が\(p_1\)、体積が\(\frac{1}{2}SL\) ですから、
\begin{eqnarray} p_0(SL)^\gamma&=&p_1(\frac{1}{2}SL)^\gamma \\
ゆえに、p_1&=&2^\gamma p_0 \\
(2-22)(2-25)式から、W_1&=&\frac{3}{2}SL(2^{\gamma-1}-1)p_0
\end{eqnarray}
となります。
さらに脱線してしまいますが、\(pV^\gamma=一定\)の式を導いておきます。
状態方程式と熱力学第一法則などの使い方に慣れ、同時に、微小変化を示す\(\Delta\)の文字の使い方のトレーニングになるからです。
断熱変化により、圧力\(p\)、体積\(V\)、絶対温度\(T\)の状態から、圧力\(p+\Delta p\)、体積\(V+\Delta V\)、絶対温度\(T+\Delta T\)の状態に変化したとします。
また、気体の定積モル比熱を\(C_V\)、定圧モル比熱を\(C_p\)、\(\gamma=\frac{C_p}{C_V}\) とします。
状態方程式は、
\begin{eqnarray} pV&=&nRT \tag{2-27} \\
(p+\Delta p)(V+\Delta V)&=&nR(T+\Delta T) \tag{2-28}
\end{eqnarray}
となります。
(2-28)式を展開します。
このとき、\(\Delta p \Delta V\)という微小量の2次の項が出ます。
この(小さな数字を二つ掛け合わせた)項は、それ以外の項に比べて非常に小さくなるはずですから、近似的に無視できると考えます。
これより、
\begin{eqnarray} pV+p\Delta V+V\Delta p&=&nR(T+\Delta T) \\
nRT+p\Delta V+V\Delta p&=&nR(T+\Delta T) \\
p\Delta V+V\Delta p&=&nR\Delta T \tag{2-29}
\end{eqnarray}
次に、熱力学第一法則を考えます。
断熱変化ですから、\(Q=0\)で、
\begin{eqnarray} 0&=&W+\Delta U \\
\\
W&=&-\Delta U=-nC_V\Delta T \\
\\
また、W&=&p\Delta V \\
これらの式より、nR\Delta T&=&-W\frac{R}{C_V}=-p\Delta V\frac{R}{C_V} \\
\\
(2-29)式から、 p\Delta V+V\Delta p&=&-p\Delta V\frac{R}{C_V} \\
移項して、p\Delta V\left(1+\frac{R}{C_V}\right)&=&-V\Delta p
\end{eqnarray}
\begin{equation} p\Delta V\frac{C_V+R}{C_V}=-V\Delta p \end{equation}
\begin{equation} \ p\Delta V\frac{C_p}{C_V}=-V\Delta p (マイヤーの関係) \end{equation}
\begin{equation} これより、\frac{\Delta p}{p}=-\gamma\frac{\Delta V}{V} \end{equation}
両辺を積分します。
積分定数を\(C\)として、
\begin{eqnarray} \int{\frac{\Delta p}{p}}&=&-\gamma\int{\frac{\Delta v}{V}} \\
\\
\log p&=&-\gamma \log V+C \\
\\
\log (pV^\gamma)&=&C \\
\\
ゆえに、pV^\gamma&=&一定 \tag{2-30}
\end{eqnarray}
ここで、(2-26)式を解釈してみましょう。
(2-26)式の右辺を書き換えると、
\begin{eqnarray} Q&=&3SL\ (p_1-p_0) \\
&=&\frac{3}{2}S\cdot 2L\cdot (p_1-p_0)=\frac{3}{2}\left(2SL\cdot p_1-2SL\cdot p_0\right)
\end{eqnarray}
となります。
この式の\(Q\)は、体積\(2SL\)中の気体の圧力を\(p_0\)から\(p_1\)に変化させるに必要な熱量を示しています。
つまり、右図2-6のように、断熱材でつくられた体積\(2SL\)の固定された容器があって、内部には単原子分子理想気体が封入されています。
初期状態では、気体の圧力は\(p_0\)です。
今、ヒータを熱して内部の圧力を\(p_1\)に増加させます。
このときヒータが供給した熱量を求めると、(2-26)式と同じになるわけです。
図2-5と図2-6ではかなり設定が違うように感じますが、同じ結果となるのは面白いですね。
さて、もう一度この問題を振り返ると、左側の部屋についても熱力学第一法則の式を立てることに気が付くことが大事であることがわかります。
計算で求められない[右の気体がした仕事]を[左の気体がした仕事]で相殺できることを見通せるかようになりたいものです。
3-2.ばねがある場合の気体のした仕事
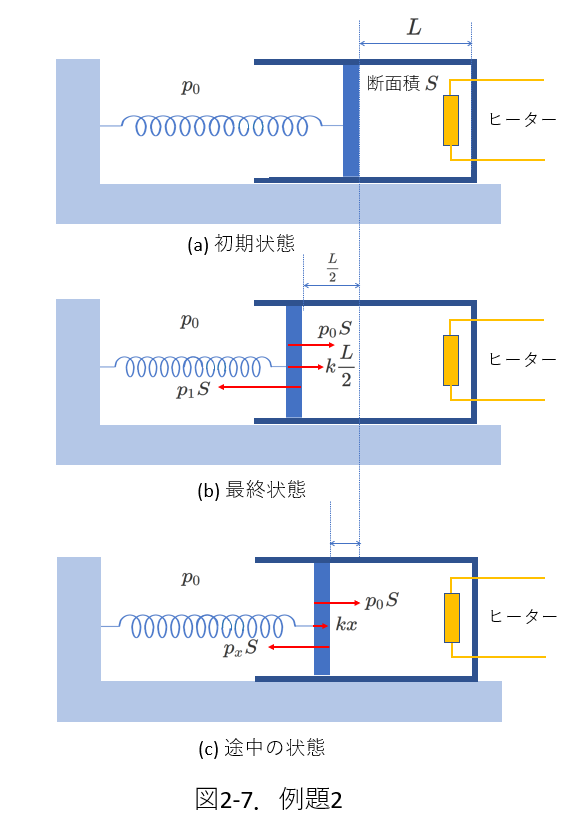
図2-7のように、台に固定された円筒の内部に、円筒に沿って自由に動くことのできるピストンがあります。
ピストンはばね定数が\(k\)のばねにつながれ、ばねの他端は台の壁に固定されています。
円筒とピストンで形成された部屋には、単原子分子理想気体が満たされています。
また、円筒の壁もピストンも断熱材でつくられていて、これらを通して熱が出入りすることはありません。
ピストンの面積、および円筒の内面の断面積はともに\(S\)です。
今、(a)のように、部屋の長さが\(L\)のとき、ばねの長さは自然長であったとします。
部屋の外部の圧力を\(p_0\)とすると、部屋の内部の圧力も\(p_0\)です。
部屋にはヒーターがあって、徐々に加熱したところピストンがゆっくり動き、最初の位置から\(\frac{1}{2}L\)離れ、(b)のような状態でピストンが静止しました。
このときにヒーターが部屋に与えた熱量を求めます。
さて、熱量を直接求めることはできません。
熱量を求めるには、多くの場合、熱力学の第一法則を用います。
熱力学第一法則によれば、熱量を求めるには、気体の内部エネルギーの変化と気体がした(あるいは、された)仕事を求めます。
内部エネルギーを求めるには、温度\(T\)がわかっているか、あるいは、圧力\(p\)と体積\(V\)の両方がわかっていることが、必要です。
(a)の状態では、部屋の体積も圧力もわかっていますから、内部エネルギーを求めることができます。
(b)のほうは、部屋の体積がわかっていますが、圧力がわかっていません。
しかし、ピストンが静止していることから、部屋の気体の圧力による力と、外部の気体の圧力\(p_0\)による力とばねの弾性力とがつり合っていると考えられます。このことから、部屋の気体の圧力\(p_1\)が求められそうです。
次に、部屋の単原子分子理想気体がした仕事を考えます。
それには2通りの方法があります。
A.仕事を直接求める方法
B.気体が仕事をしたことによる変化から求める方法
のふたつです。
最初にAの方法で考えます。
ピストンがゆっくり動いていったことから、(a)から(b)に至る途中でも、ピストンに加わる力がつりあっていると考えて、部屋の単原子分子理想気体の圧力が求められます。
この圧力を、ピストンの変位(したがって、部屋の体積変化)で表すことができれば、\(p-V\)グラフの面積から、部屋の気体がした仕事を求めることができます。
手順をまとめると次のようになります。
①力のつりあいから、\(p_1\)の値、および、(a)から(b)への過程の途中における気体の圧力を求める
②内部エネルギーの変化量を求める \(\frac{3}{2}\Delta (PV)、または、\frac{3}{2}nR\Delta T\)
③\(p-V\)グラフ等を使って、気体のした仕事を求める
④熱力学の第一法則
まず、①から、
図2-7(c)を参照すると、(a)から(b)の途中の過程で、ピストンの変位を\(x\)、圧力を\(p_x\)とすると、ピストンに加わる力のつりあいを表す式は次のようになります。
\begin{eqnarray} kx+p_0S&=&p_xS \tag{2-31} \\
p_x&=&p_0+\frac{kx}{S} \tag{2-32} \\
この式より、p_1&=&p_0+\frac{kL}{2S} \tag{2-33}
\end{eqnarray}
②内部エネルギーの変化量\(\Delta U\)を求めます。
\begin{eqnarray} \Delta U&=&\frac{3}{2}\Delta(PV) \\
&=&\frac{3}{2}p_1\cdot \frac{3}{2}LS-\frac{3}{2}p_0\cdot LS \\
&=&\frac{3}{2}\left(p_0+\frac{kL}{2S}\right) \cdot \frac{3}{2}LS-\frac{3}{2}p_0\cdot LS \\
&=&\frac{3}{4}p_0LS+\frac{9}{8}kL^2 \tag{2-34}
\end{eqnarray}
③の準備として\(p-V\)グラフを描きます。
状態(a)、状態(b)の圧力および体積は、(2-33)式などから、グラフにプロットできます。
また、(2-32)式を見ると、状態(a)から状態(b)までは\(p-V\)グラフ上で直線で表されることがわかります。
もう少しわかりやすくするため、変位が\(x\)のときの体積を\(V_x\)とすれば、\(V_x=LS+xS\)、つまり、\(x=\frac{V_x}{S}-L\)で、これを(2-32)に代入すれば、
\begin{eqnarray} p_x&=&p_0+\frac{kx}{S} \tag{2-35} \\
&=&p_0+\frac{k(\frac{V_x}{S}-L)}{S} \\
&=&p_0-\frac{kL}{S}+\frac{k}{S^2}\cdot V_x \tag{2-36}
\end{eqnarray}
この式から、\(p_x\)は\(V_x\)に対して直線的に変化することがわかります。
注) このような式を立てたら、\(V_x=LS\)や\(V_x=\frac{3}{2}LS\)を代入して、式が正しく求められていることを確認する習慣をつけましょう。
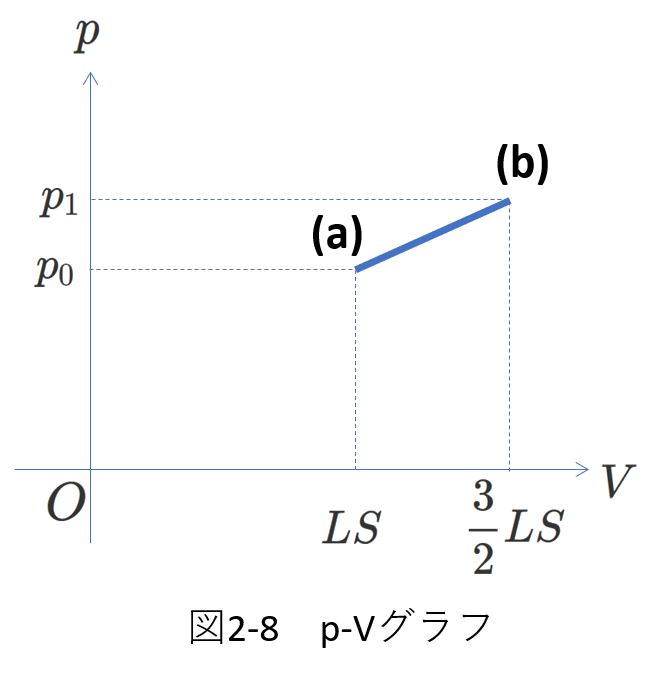
\(p-V\)グラフを描けば右の図のようになります。
図2-7のように、ピストンにばねが繋がっている場合、(a)から(b)への過程は\(p-V\)グラフ上で直線になることを頭の隅に入れておきましょう。
気体が外部にした仕事\(W\)は、図2-8の\(p-V\)グラフの線分(a)(b)と\(V=LS\)と\(V=\frac{3}{2}LS\)と\(V\)軸に囲まれた台形の面積に等しいことと、(2-33)式から、
\begin{eqnarray} W&=&\frac{1}{2}\left(p_0+p_1\right)\left(\frac{3}{2}LS-LS\right) \\
&=&\frac{1}{2}p_0LS+\frac{1}{8}kL^2 \tag{2-37} \\
&=&p_0\cdot \frac{1}{2}LS+\frac{1}{2}k\left(\frac{L}{2}\right)^2 \tag{2-38}
\end{eqnarray}
④これより、気体に加えられた熱量\(Q\)は次のようになります。
\begin{eqnarray} Q&=&\Delta U+W \\
&=&\frac{3}{4}p_0LS+\frac{9}{8}kL^2+\frac{1}{2}p_0LS+\frac{1}{8}kL^2 \\
&=&\frac{5}{4}p_0LS+\frac{5}{4}kL^2 \tag{2-39}
\end{eqnarray}
では、Bの方法で気体がした仕事を求めることができることを説明します。
(2-37)式の\(W\)の式を、(2-38)式のように変形すると、第1項は[外部の気体が受けた仕事]です。
そして、第2項は[ばねに蓄えられた弾性エネルギー]です。 つまり、
[気体がした仕事]=[外部の気体が受けた仕事]+[ばねに蓄えられた弾性エネルギー] (2-40)
です。
上の(2-40)式の右辺を計算するのがBの方法です。
このほうが計算が楽かもしれません。
つまり、[気体がした仕事]は、「外部気体」と「ばね」が受け取ったわけで、[外部気体が受けた仕事]と「ばねが蓄えている弾性エネルギー」を求めれば、[気体がした仕事」は求められます。
[外部の気体が受けた仕事]と[ばねに蓄えられた弾性エネルギー」について、「した仕事」と「された仕事」でその符号がどう変わるかをまとめると、
「外部の気体がピストンにした仕事」は、外部気体の圧力とピストンが進む向きが逆で、変位は\(\frac{L}{2}\)であること、外部の圧力は一定であることから、
[外部の気体がピストンにした仕事]=\(-\frac{1}{2}p_0LS\)
[外部の気体がピストンから受けた仕事]=-[外部の気体がピストンにした仕事]=\(\frac{1}{2}p_0LS\)
です。
また、[弾性力がピストンにした仕事]は、弾性力とピストンの進む向きが逆であること、弾性力はピストンの変位によって変化することに注意して、
[弾性力がピストンにした仕事]=\(-\frac{1}{2}k\left(\frac{L}{2}\right)^2\)
[ばねに蓄えられた弾性エネルギー]=-[弾性力がピストンにした仕事]=\(\frac{1}{2}k\left(\frac{L}{2}\right)^2\)
となります。
3-3.さらに重力が加わりました
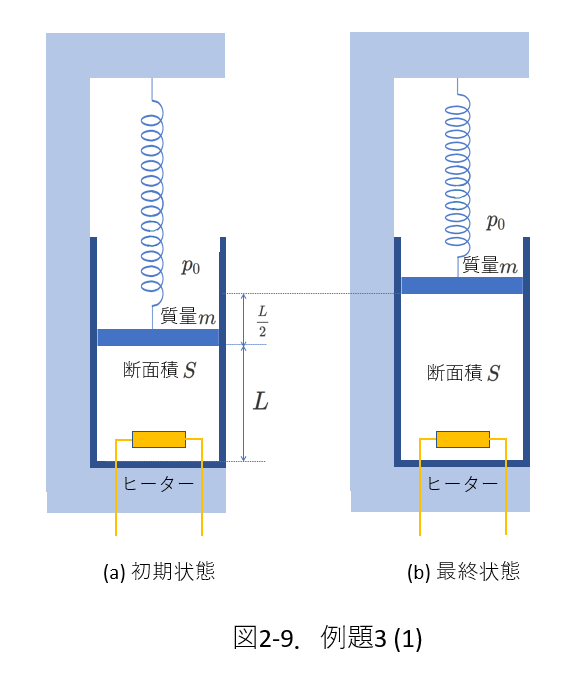
今度は、図2-9のように、図2-7を鉛直方向に立ててみます。
そして、シリンダーとピストンに囲まれた部屋の中の理想気体をヒータで加熱して、(a)初期状態から(b)最終状態に状態を変えます。
シリンダーとピストンで形成された部屋には、単原子分子理想気体が満たされています。
そして、シリンダーもピストンも熱を伝えない材料で作られていて、シリンダーの壁やピストンを通して熱が出入りすることはありません。
ピストンの面積、および、シリンダーを鉛直方向に垂直な面で切ったときの内面の断面積はともに\(S\)です。
今、(a)のように、部屋の長さが\(L\)のとき、ばねは長さ\(l\)だけ伸びていたとします。
外部の気体の圧力は\(p_0\)で、ピストンの位置により変化はしないものとします。
部屋にあるヒーターを加熱して、ピストンを徐々に上昇させ、最初の位置から\(\frac{1}{2}L\)だけ上昇したところでピストンが静止しました。
このときにヒーターが部屋に与えた熱量を求めます。
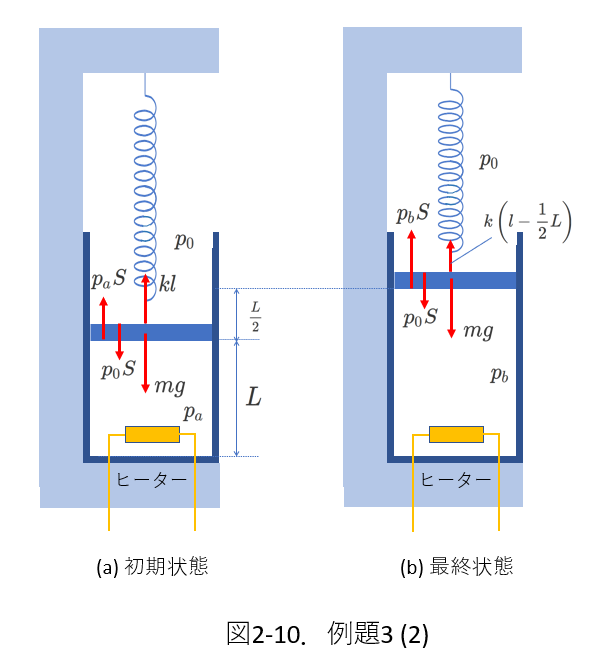
状態(a)(b)における圧力(それぞれ、\(p_a\)、\(p_b\)とします)を、ピストンが受ける力のつりあいから求めます。
図2-9にピストンが受ける力を描き入れたものを、図2-10に示します。
図2-10(a)を元にして力のつりあいの式を立てると、
\begin{eqnarray} p_aS+kl&=&p_0S+mg \tag{2-41} \\
p_a&=&p_0+\frac{mg}{S}-\frac{kl}{S} \end{eqnarray}
図2-10(b)から、
\begin{eqnarray} p_bS+k\left(l-\frac{1}{2}L\right)&=&p_0S+mg \\
p_b&=&p_0+\frac{mg}{S}-\frac{k\left(l-\frac{1}{2}L\right)}{S} \tag{2-42} \end{eqnarray}
では、内部エネルギーの変化量\(\Delta U\)を求めます。
\begin{eqnarray} \Delta U&=&[変化後の内部エネルギー]-[変化前の内部エネルギー] \\
&=&\frac{3}{2}[変化後の圧力][変化後の体積]-\frac{3}{2}[変化前の圧力][変化前の体積] \\
&=&\frac{3}{2}p_bSL\cdot\left(1+\frac{1}{2}\right)-\frac{3}{2}p_aSL \\
&=&\frac{3}{2}\left(p_0+\frac{mg}{S}-\frac{k\left(l-\frac{1}{2}L\right)}{S}\right)S\cdot\frac{3}{2}L-\frac{3}{2}\left(p_0+\frac{mg}{S}-\frac{kl}{S}\right)SL \\
&=&\frac{3}{4}SL\left(p_0+\frac{mg}{S}-\frac{kl-\frac{3}{2}kL}{S}\right) \tag{2-43}
\end{eqnarray}
この計算結果を簡単にチェックする意味で、\(g\)と\(l\)に\(0\)を代入してみます。
これにより、問題の条件が「3-2.ばねがある場合の気体のした仕事」の問題の条件と同じになりますから、\(\Delta U\)の値は、(2-34)式に等しくなるはずです。
代入します。
\begin{eqnarray} \Delta U&=&\frac{3}{4}SL\left(p_0+\frac{m\cdot 0}{S}-\frac{k\cdot 0-\frac{3}{2}kL}{S}\right) \\
&=&\frac{3}{4}SL\left(p_0+\frac{3kL}{2S}\right) \tag{2-44}
\end{eqnarray}
両式で同じミスをしている可能性もあるので正しいことが保証されるわけではないですが、(2-34)式と一致したことは、(2-43)式が正しいことをある程度保証しています。
次に、気体がした仕事を求めます。
この例題では、最初にBの方法を用います。
移動距離は\(\frac{1}{2}L\)ですが、ばねの弾性力が関与しているため、気体の圧力(力)はピストンの移動距離により変化します。
と言っても、線形の変化ですから、[気体のした仕事]は\(p-V\)グラフを使って面積から求めたり、積分を使って求めることができます。
ここでは、それらとは違って、先ず、[気体がした仕事]が何に変化したかを考えることにします。 ( (2-40)式で考察したことを応用します。)
[気体がした仕事]は、[外部の気体がされた仕事]と[ピストンの重力による位置エネルギーの変化量(増加量)]と[弾性エネルギーの変化量(増加量)]に変わったと考えることができます。
つまり、
[気体がした仕事]=[外部の気体がされた仕事]+[ピストンの位置エネルギーの変化量]+[弾性エネルギーの変化量] (2-45)
最初に、[外部の気体がされた仕事]を考えます。
なんとなく、[外部の気体がされた仕事]=\(p_0S\cdot \frac{L}{2}\)だと分かりますが、きっちり考えましょう。
[外部の気体がされた仕事]=-[外部の気体がした仕事]で、[外部の気体がした仕事]=-\(p_0S\cdot \frac{L}{2}\)です。
外部の気体がピストンを押す向きと、ピストンが動く向きが反対ですから、外部の気体がピストンを押す力がする仕事は負となります。
以上より、
\begin{equation} [外部の気体がされた仕事]=p_0S\cdot \frac{L}{2} \tag{2-46} \end{equation}
です。
次に、[位置エネルギーの変化量]です。
気体は、ピストンに仕事をして、ピストンの位置エネルギーを\(mg\frac{1}{2}L\)増加させましたから、
\begin{equation} [ピストンの位置エネルギーの変化量]=\frac{1}{2}mgL \tag{2-47} \end{equation}
です。
[弾性エネルギーの変化量]は、
最初の状態で、ばねの伸びは\(l\) でしたから、弾性エネルギーは、\(\frac{1}{2}kl^2\) です。
最終状態では、ばねの伸びは\(\left(l-\frac{1}{2}L\right)\) ですから、弾性エネルギーは、\(\frac{1}{2}k\left(l-\frac{1}{2}L\right)^2\)です。
したがって、
\begin{equation} [弾性エネルギーの変化量]=\frac{1}{2}k\left(l-\frac{1}{2}L\right)^2-\frac{1}{2}kl^2 \tag{2-48} \end{equation}
となります。
このとき間違いやすいのは、[最初の状態]-[最終状態]と、引き算の順序を逆にしてしまうことや、変化量を\(\frac{1}{2}k\left(\frac{1}{2}L\right)^2\)というように、[伸び]の変化量から求めてしまうなどです。
弾性エネルギーは\([伸び]^2\)に比例しますから、[伸び]の差から弾性エネルギーの差を求めることはできません。
さて、(2-45)式から、
\begin{eqnarray} [気体がした仕事]W&=&p_0S\cdot \frac{L}{2}+\frac{1}{2}mgL+\frac{1}{2}k\left(l-\frac{1}{2}L\right)^2-\frac{1}{2}kl^2 \\
&=&\frac{1}{2}p_0SL+\frac{1}{2}mgL+\frac{1}{2}kL\left(-l+\frac{1}{4}L\right) \tag{2-49}
\end{eqnarray}
この式に、\(g=0\)、\(l=0\)を代入すると、
\begin{eqnarray} W&=&\frac{1}{2}p_0SL+\frac{1}{2}mL\cdot 0+\frac{1}{2}kL\left(-0+\frac{1}{4}L\right)
&=&\frac{1}{2}p_0SL+\frac{1}{8}kL^2 \tag{2-50}
\end{eqnarray}
この式は、(2-37)式に一致しました。
熱力学の第一法則から、[気体が吸収した熱量]\(Q\)は、
\begin{eqnarray} Q&=&\frac{3}{4}SL\left(p_0+\frac{mg}{S}-\frac{kl-\frac{3}{2}kL}{S}\right)+\frac{1}{2}p_0SL+\frac{1}{2}mgL+\frac{1}{2}kL\left(-l+\frac{1}{4}L\right) \\
&=&\frac{5}{4}\left(p_0S+mg-kl+kL\right)L \tag{2-51}
\end{eqnarray}
気体のした仕事\(W\)を(2-45)式から求めましたが、シリンダーの中の気体の力から求めてみます。
つまり、Aの方法を用います。
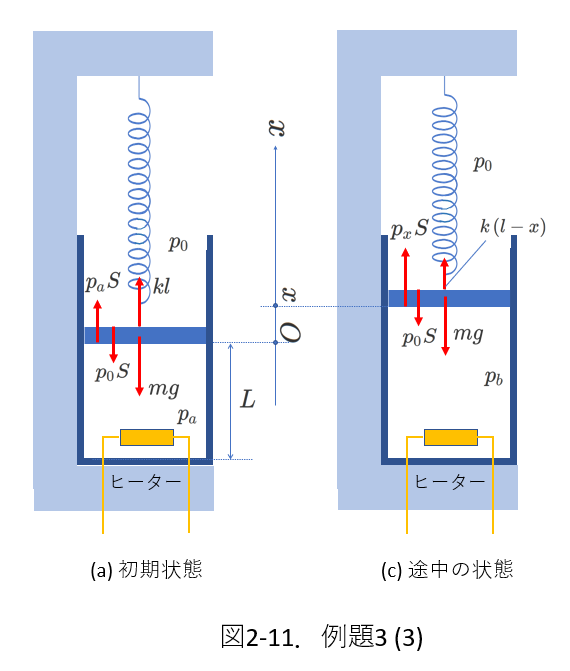
図2-11(c)にピストンが移動している途中の状態でピストンに働く力を示しました。
ここで、ピストンの初期位置を原点として鉛直上向きの\(x\)軸を考えます。そして、ピストンの座標を\(x\)とします。
こうすると、ばねの伸びは\((l-x)\)で表されます。
\(x=0\)で伸びは\(l\)、\(x=l\)では伸びは\(0\)で、ばねは自然長になります。
さらに、\(x\)が増加すると、\((l-x)\lt 0\)となり、負の伸びは、ばねが縮んでいる状態だとわかります。
したがって、弾性力は\(k(l-x)\)と表されます。
(この式は\(x\)が正でも負でもそのまま使えます。)
ピストンは非常にゆっくり等速度運動をしていると考えることができますから、途中の状態でもピストンにはたらく力はつりあっていると考えることができて、次の式が導かれます。
\begin{eqnarray} p_xS+k(l-x)&=&p_0S+mg \tag{2-52} \\
p_x&=&p_0+\frac{mg}{S}-\frac{k(l-x)}{S} \tag{2-53}
\end{eqnarray}
(2-46)式で気体の圧力を\(p_x\)と表しています。
気体の圧力による力がする仕事は、力の大きさが\(p_xS\)、そのときの変位を\(\Delta x\)として、\(p_xS\Delta x\)と表されます。
この場合は、力\(p_xS\)が一定ではないので、各\(x\)で\(p_xS\Delta x\)を計算して足し合わせる、つまり、積分することになります。
したがって、
\begin{eqnarray} W&=&\int_0^\frac{L}{2} p_xSdx \\
&=&\int_0^\frac{L}{2} \left(p_0S+mg-k(l-x)\right)dx \\
&=&\int_0^\frac{L}{2} \left((p_0S+mg-kl)+kx\right)dx \\
&=&\left[(p_0S+mg-kl)x\right]_0^\frac{L}{2}+\left[\frac{k}{2}x^2\right]_0^\frac{L}{2} \\
&=&(p_0S+mg-kl)\frac{L}{2}+\frac{1}{8}kL^2 \tag{2-54}
\end{eqnarray}
これは、(2-49)式と一致します。
積分で正しい答えが得られましたが、\(p-V\)グラフの面積を使って、気体のした仕事\(W\)を求めることもできます。
(2-53)式を使って、(a)初期状態から(b)最終状態への過程を\(p-V\)グラフに表します。
(2-53)式で圧力\(p_x\)は既に式の中に含まれているので、体積\(V\)を(2-53)式に導入することになります。
これは、変数\(x\)を使って、変数の体積\(V\)を表すことで得られます。
\(V=S(L+x)\) と表されます。
したがって、\(x=\frac{V}{S}-L\)
これを、(2-53) 式に代入して、
\begin{eqnarray} p_x&=&p_0+\frac{mg}{S}-\frac{kl}{S}+\frac{k}{S}\left(\frac{V}{S}-L\right) \\
&=&p_0+\frac{mg-kl-kL}{S}+\frac{k}{S^2}V \tag{2-55}
\end{eqnarray}
(2-55)式のグラフは、\(p-V\)グラフ上で直線になります。
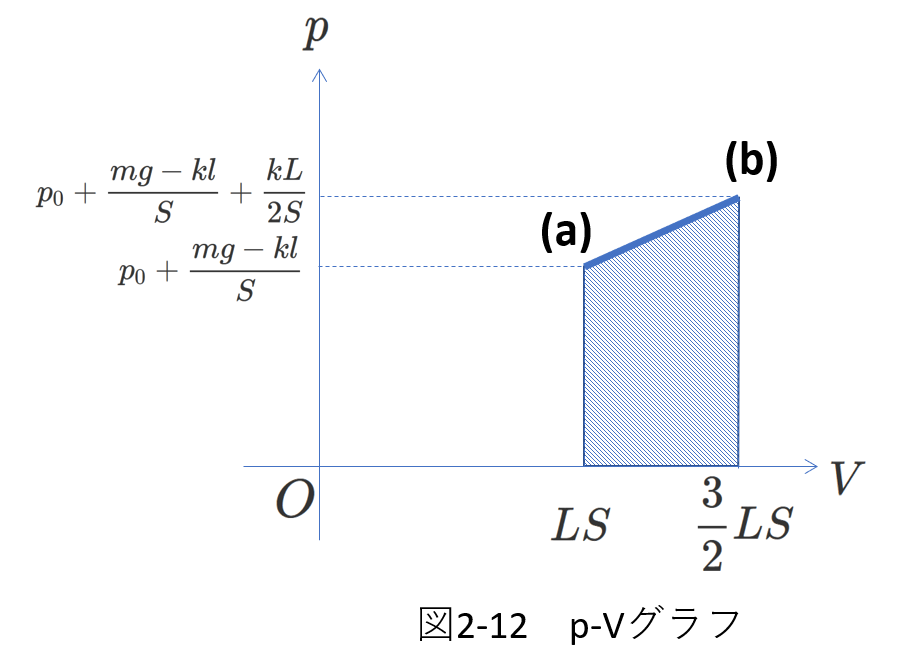
(a)初期状態の\(V=SL\)を代入すると、\(p_a=p_0+\frac{mg-kl}{S}\)、(b)最終状態の\(V=\frac{3}{2}SL\)を代入すると、\(p_b=p_0+\frac{mg-kl+\frac{1}{2}kL}{S}\)で、それぞれ(2-41)式(2-42)式と一致していることから、(2-55)式が正しい式と考えてよさそうです。
また、\(p_a\lt p_b\)であることもわかります。
以上より、\(p-V\)グラフは、右図2-12のようになります。
斜線で示す部分の面積が、気体が外部に対してする仕事の大きさになります。
(a)→(b)で体積は増加しているので、気体が外部にする仕事は正であることがわかります。
この面積を計算すれば、(2-54)式と同じ結果になります。
確認してください。
例題からはなれて、ここで、(2-45)式を、[受けた仕事]=[運動エネルギーの変化量]の関係を使って導きます。
(同様の説明を、(2-17)式でもしています。)
つまり、図2-10において、ピストンは初期状態、最終状態とも運動エネルギーは\(0\)と考えることができます。
そして、この間にピストンは、[内部の気体の圧力による力]、[外部の気体の圧力による力]、[重力]、[ばねの弾性力]から仕事をされます。
すなわち、
\(\frac{1}{2}m\cdot 0^2-\frac{1}{2}m\cdot 0^2=\)[気体がピストンにした仕事]+[外部の気体がピストンにした仕事」
+[重力がピストンにした仕事]+[ばねの弾性力がピストンにした仕事] (2-56)
ここで、
[外部の気体がピストンにした仕事]=-[外部の気体がされた仕事]
[重力がピストンにした仕事]\(=-mg\cdot \frac{L}{2}=-\)[ピストンの位置エネルギーの変化量]
[ばねの弾性力がピストンにした仕事]=-[ピストンから仕事をされて変化した弾性エネルギーの量]=-[ばねの弾性エネルギーの変化量]
を(2-56)式に代入して、
0=[気体がした仕事]-[外部の気体がされた仕事]-[ピストンの位置エネルギーの変化量]-[ばねの弾性エネルギーの変化量]
移項して
[気体がした仕事]=[外部の気体がされた仕事]+[ピストンの位置エネルギーの変化量]+[ばねの弾性エネルギーの変化量]
となり、(2-45)が導かれました。
関連ページ
- p-Vグラフ Ⅱ
- 「熱と気体」分野で学んでおくべき内容を項目に分けて説明しています。