Ⅰ.仕事と内積
仕事が数学の内積で表されることを説明しています。
内積については数学で勉強しているので詳しくは述べません。
ポイントを示すと、
内積は、\(\vec{A}\cdot\vec{B}\) と表されて、
\(\vec{A}=(x_1,y_1)\)、\(\vec{B}=(x_2,y_2)\) のとき、
\(\vec{A}\cdot\vec{B}=x_1x_2+y_1y_2\) です。
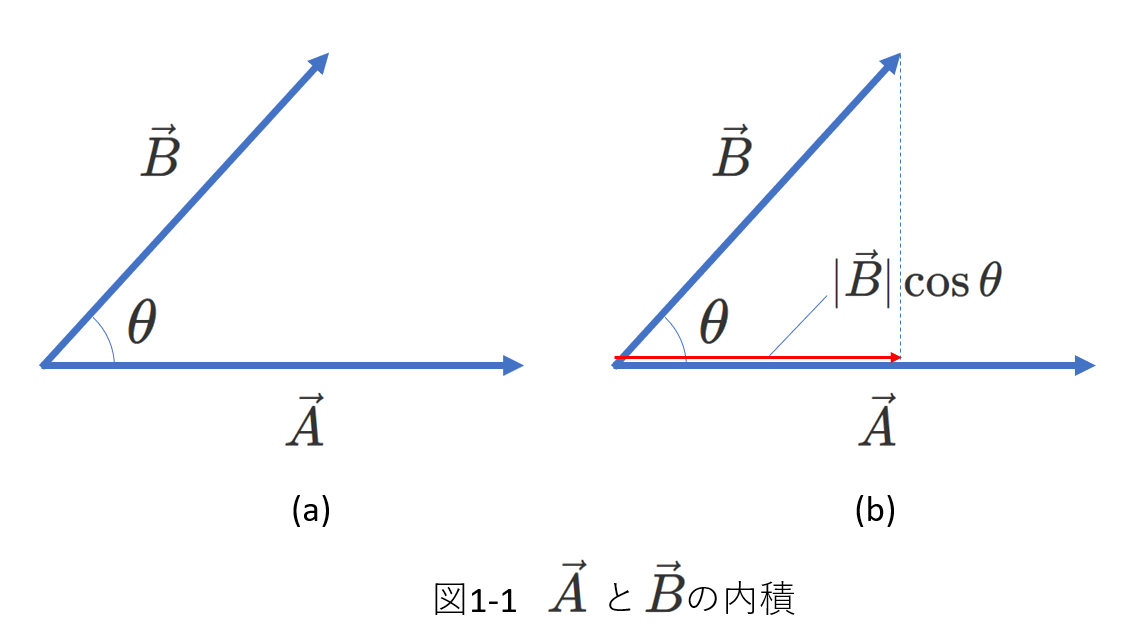
また、\(\vec{A}\)と\(\vec{B}\)の関係が右図1-1(a)に示すように、ふたつのベクトルの角度が\(\theta\)のとき、
\(\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos\theta\) です。
ここで、\(\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos\theta=|\vec{A}|\left(|\vec{B}|\cos\theta\right)\) と考えると、図1-1(b)に示すように、\(\vec{A}\)と\(\vec{B}\)の内積は、ベクトル\(\vec{B}\)の、ベクトル\(\vec{A}\)の方向の成分とベクトル\(\vec{A}\)の大きさを掛けたものであるとわかります。
もちろん、\(\vec{A}\cdot\vec{B}=|\vec{B}|\left(|\vec{A}|\cos\theta\right)\) と考えて、\(\vec{A}\)と\(\vec{B}\)の内積は、ベクトル\(\vec{A}\)の、ベクトル\(\vec{B}\)の方向の成分とベクトル\(\vec{B}\)の大きさを掛けたものと解釈することもできます。
また、\(\vec{A}\)と\(\vec{B}\)はベクトルですが、その内積\(\vec{A}\cdot\vec{B}\)はスカラーです。
では、仕事について考えます。
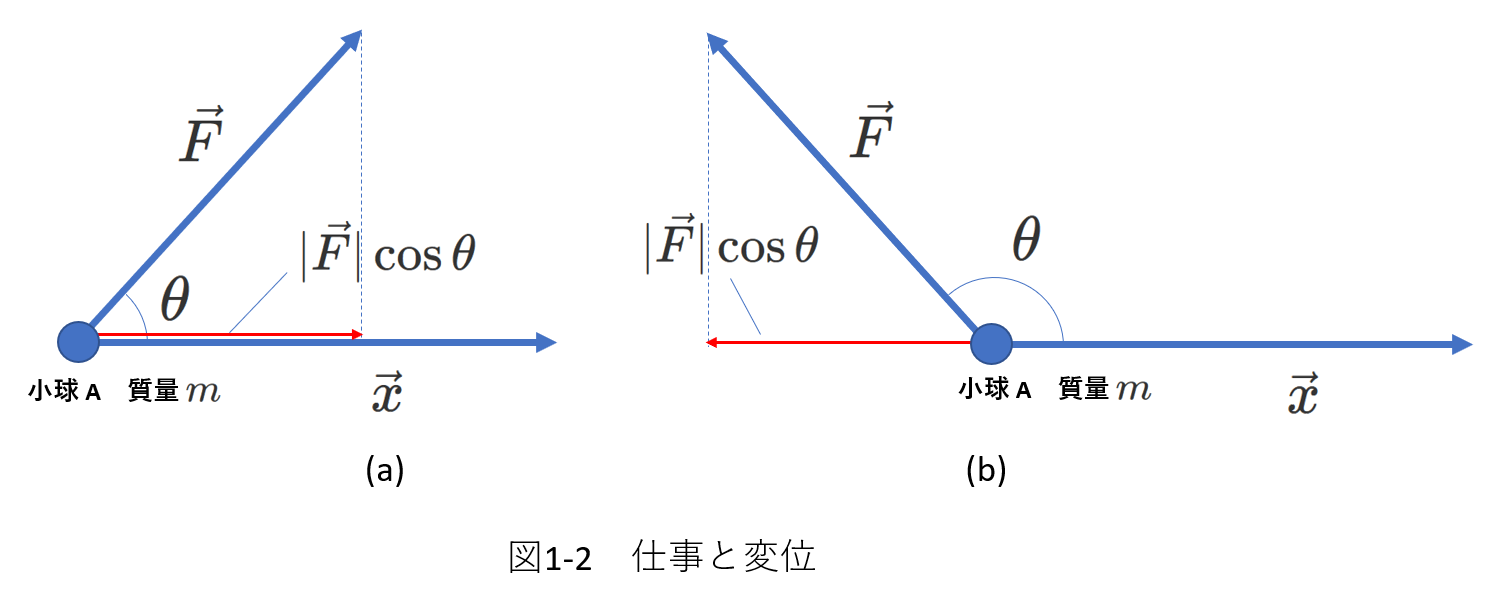
図1-2で、\(\vec{F}\)は小球\(A\)が受ける力、\(\vec{x}\)は\(A\)の変位を表します。
\(\vec{F}\)と\(\vec{x}\)の角度を\(\theta\)として、仕事の大きさは\(|\vec{F}||\vec{x}|\cos\theta\)、つまり、内積 \(\vec{F}\cdot\vec{x}\)です。
あらためて言えば、仕事は力\(\vec{F}\)の変位\(\vec{x}\)の方向の成分と変位\(|\vec{x}|\)を掛けたものであり、力と変位はベクトルですが、仕事はスカラーです。
様々な物理量について、ベクトルなのか、スカラーなのかを明確に区別して覚える必要があります。
図1-2について補足すると、
\(\theta=\frac{\pi}{2}\)のときには、\(\cos\theta=0\)ですから、仕事は\(0\)です。
物体の変位の方向に垂直にはたらく力は仕事をしません。
その例がローレンツ力で、ローレンツ力は、常に物体の速度に垂直ですから、仕事をしません。
次に、
\(\theta\gt\frac{\pi}{2}\)のときには、\(\cos\theta\lt0\)ですから、仕事は負になります。
つまり、力の向きが、物体の変位の向き(または、物体が進む向き)と逆のときには、その力が物体にする仕事は負になります。
問題をあわてて解く場合には符号ミスをしやすくなりますから、十分注意しましょう。
さて、次の3つの表現は同じ意味です。
・力が物体にする仕事は負になります。
・物体が力から受ける仕事は負になります。
・物体が力にされた仕事は負になります。
表現は色々ありますが、力が物体に仕事をしているという状況は同じですから、上の3つのどの表現を用いても仕事は同じです。
物理の問題では、\(\theta\)は\(0、\frac{\pi}{2}、\pi\)の3つのうちのどれかということが多いです。
それ以外の場合には、力の変位方向成分を考えて解くので、内積の\(\cos\theta\)を意識することはありません。
そのような例をひとつあげておきます。
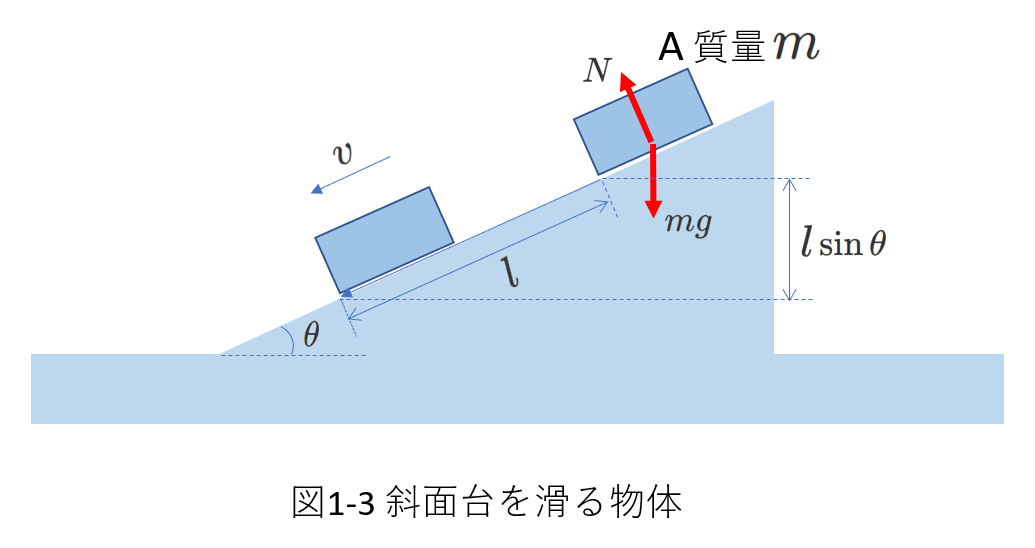
右図1-3では、水平面との角度が\(\theta\)の斜面上に質量\(m\)の物体を置き、静かに手を離したところ斜面上を距離\(l\)すべって速さが\(v\)になりました。斜面と物体の間には摩擦はないものとして、\(v\)を求めてみます。
① 通常、この問題は力学的エネルギー保存の式を使います。
重力の位置エネルギ-の基準を、最初に\(A\)が置かれたところとします。
斜面上を\(l\) 進むことは、鉛直方向に\(l\sin\theta\)進むことになるので、力学的エネルギー保存の式は、
\begin{eqnarray} \frac{1}{2}m\cdot 0^2+mg\cdot 0&=&\frac{1}{2}mv^2+(-mgl\sin\theta) \tag{1-1} \\
v&=&\sqrt{2gl\sin\theta} \tag{1-2}
\end{eqnarray}
となります。
② 次に、重力がした仕事に注目して\(v\)を求めます。
図1-3で、\(A\)にはたらく力は重力\(mg\)と垂直抗力\(N\)です。
\(N\)は物体が進む方向と垂直ですから、\(N\)は物体に仕事をしません。
つまり、物体の運動エネルギーを変えません。言い換えれば、物体の速度を変えません。
一方、重力は鉛直方向にはたらき、物体の進む方向の成分を持ちます。
つまり、重力は物体に対して仕事をし、物体の速度を変えます。
仕事と運動エネルギーの変化量の関係を使って、
重力が物体に仕事をしたことにより、物体の運動エネルギーが変化した、という式を立てます。
ここで、重力が物体にした仕事は、重力の斜面方向成分\(mg\sin\theta\)が \(l\) だけ変位する間にはたらいていたと考えて、\(lmg\sin\theta\)です。
仕事と運動エネルギーの変化量の関係を式に表せば、
\begin{eqnarray} \frac{1}{2}mv^2-\frac{1}{2}m\cdot 0^2&=&lmg\sin\theta \tag{1-3} \\
v=\sqrt{2gl\sin\theta}
\end{eqnarray}
(1-2)式と一致しました。
ここでは、重力の変位方向成分(斜面方向成分)を求め、[重力の変位方向成分]×[変位の大きさ]を計算しています。
内積をまったく意識しなくても簡単に解けます。
③ もちろん、同様のことを内積を使って考えることもできます。
\begin{eqnarray} \frac{1}{2}mv^2-\frac{1}{2}m\cdot 0^2&=&m\vec{g}\cdot\vec{l} \tag{1-4} \\
m\vec{g}\cdot\vec{l}&=&mgl\cos\left(\frac{\pi}{2}-\theta\right)=lmg\sin\theta \tag{1-5}
\end{eqnarray}
ここで、重力加速度ベクトルを\(\vec{g}\)、物体の変位ベクトルを\(\vec{l}\)と表しました。
また、\(\vec{g}\)と\(\vec{l}\)の間の角度は\(\left(\frac{\pi}{2}-\theta\right)\)です。
(1-3)式と同じ式が得られました。
上の例では、「内積を使わなくても解ける」という話をしましたが、
次に「ベクトルを用いて、仕事を内積で表すとわかりやすい」という例も示しておきましょう。
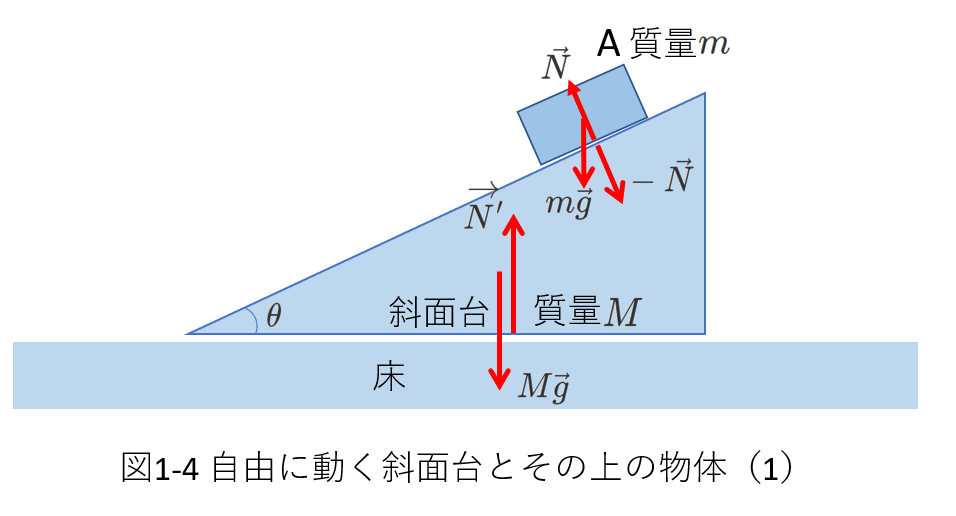
右図1-4は、図1-3とは異なり、床の上に置かれた斜面台が床上で(摩擦なしに)自由に動きます。
斜面台の上には、物体\(A\)が置かれています。
最初は固定されていた斜面台と物体を、時刻\(0\)で同時に静かに放したとします。
このあと、物体と斜面台の力学的エネルギーの和が保存されることを示します。
図1-4には、物体と斜面台に働く力が図示されています。
このうち、重力(\(m\vec{g}\)と\(M\vec{g}\))は保存力です。
非保存力は、垂直抗力(\(\vec{N}\)と\(\vec{N'}\))です。
また、物体が斜面台から受ける垂直抗力を\(\vec{N}\)と表しているので、その反作用である斜面台が物体から受ける垂直抗力は\(-\vec{N}\)と表されます。
斜面台は水平方向に運動するだけですから、鉛直上向きの垂直抗力\(\vec{N'}\) は、斜面台に仕事をしません。
したがって、物体と斜面台の間に働く垂直抗力が物体と斜面台にする仕事の和が\(0\)であることを示せば、物体と斜面台の力学的エネルギーの和が保存されることが示されることになります。
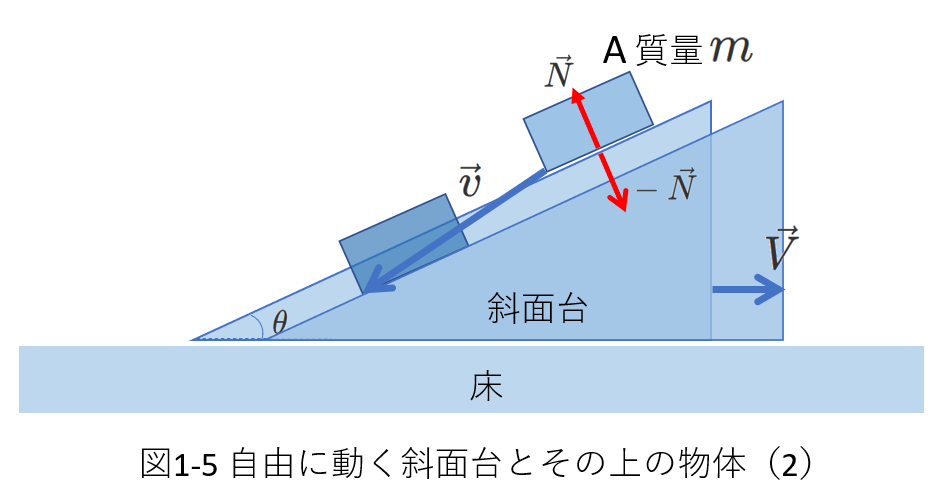
時間\(\Delta t\)の間に物体と斜面台は図1-5のように動きます。
床から見た物体の速度を\(\vec{v}\)、斜面台の速度を\(\vec{V}\)とすると、
\(\Delta t\)の間に、\(\vec{N}\)が物体にする仕事は、
\(\vec{N}\cdot\vec{v}\Delta t\)
\(-\vec{N}\)が斜面台にする仕事は、
\(-\vec{N}\cdot\vec{V}\Delta t\)
です。
垂直抗力が物体と斜面台からなる系にする仕事の和を\(\Delta W\)とすると、
\begin{eqnarray}
\Delta W&=&\vec{N}\cdot\vec{v}\Delta t-\vec{N}\cdot\vec{V}\Delta t \\
&=&\vec{N}\cdot\left(\vec{v}-\vec{V}\right)\Delta t \tag{1-6}
\end{eqnarray}
となります。
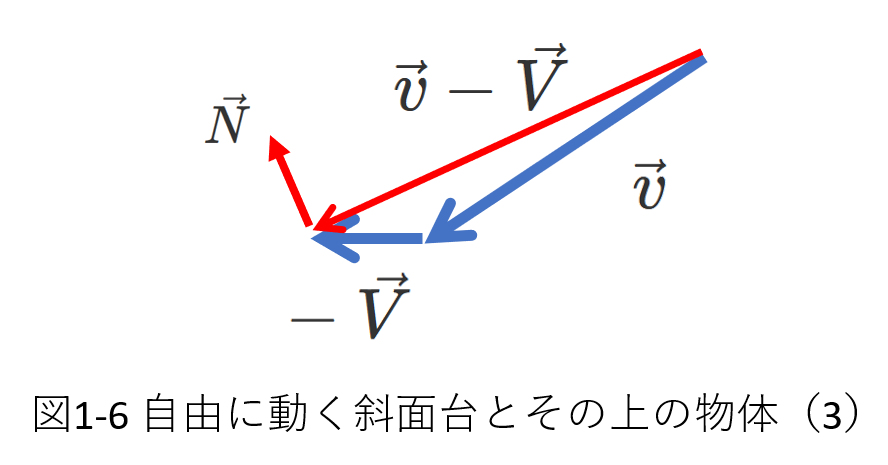
(1-6)式の\((\vec{v}-\vec{V})\)を含めたベクトル図を図1-6に示します。
ここで、\((\vec{v}-\vec{V})\)は斜面台から見た物体の速度を示しています。
そして、この相対速度の向きは斜面台の斜面に平行です。
一方、垂直抗力\(\vec{N}\)は斜面台の斜面に垂直ですから、\((\vec{v}-\vec{V})\)と\(\vec{N}\)は垂直だとわかり、
\begin{equation}
\vec{N}\cdot (\vec{v}-\vec{V})=0 \tag{1-7}
\end{equation}
ゆえに、\(\Delta W=0\)となり、物体と斜面台からなる系で力学的エネルギーが保存されることがわかりました。
Ⅱ.外積とローレンツ力
ローレンツ力が数学の外積で表されることを説明しています。
内積があれば、外積もあります。
外積は大学で習いますが、その特徴を知っていると物理が理解しやすくなるので、ここで簡単に紹介します。
ベクトル\(\vec{A}\)とベクトル\(\vec{B}\)の外積を\(\vec{A}\times\vec{B}\)と表します。
重要なのは、外積の演算結果はベクトルだということです。
(内積の演算結果はスカラーでした。)
ベクトルだということは、大きさと向きがあるということです。
最初に大きさですが、
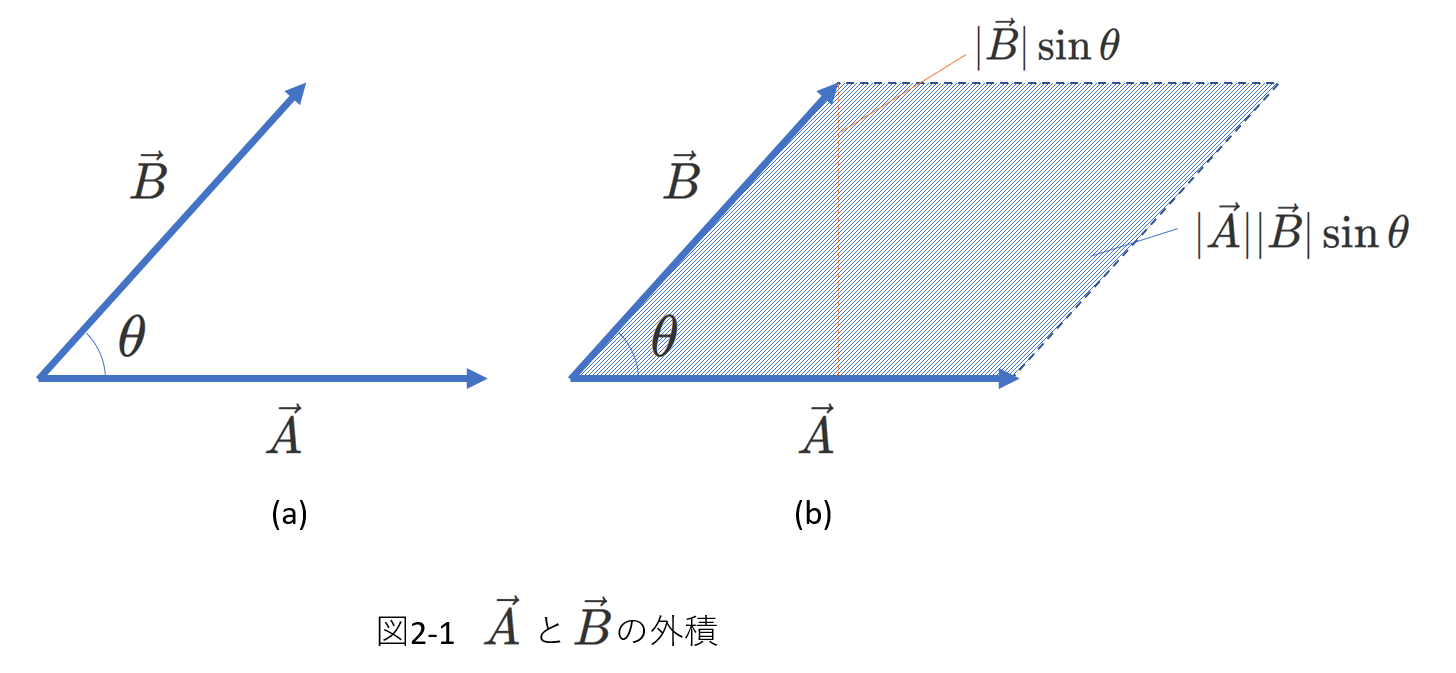
\begin{equation} |\vec{A}\times\vec{B}|=|\vec{A}||\vec{B}|\sin\theta \tag{2-1} \end{equation}
右の図2-1を見てください。
\(|\vec{A}||\vec{B}|\sin\theta\)は\(\vec{A}\)と\(\vec{B}\)がつくる平行四辺形の面積を表しているのがわかります。
内積が\(\cos\theta\)であるのに対して、外積は\(\sin\theta\)です。
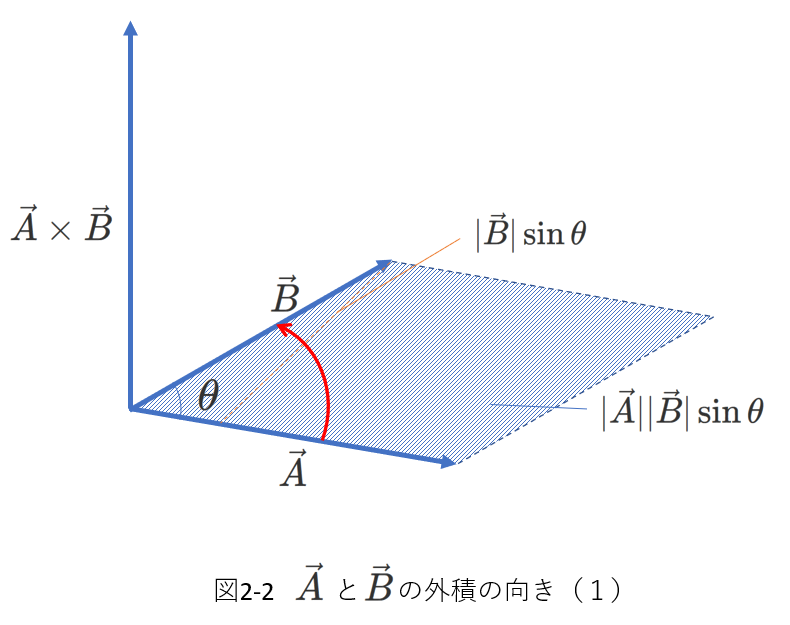
次に、\(\vec{A}\times\vec{B}\)の向きは、\(\vec{A}\)と\(\vec{B}\)のいずれとも垂直な方向(\(\vec{A}\)と\(\vec{B}\)が存在する平面に垂直)で、向きは右ねじの法則に従います。
つまり、ベクトルを\(\vec{A}\)から\(\vec{B}\)へ、角度の小さい側を通って回そうとしたとき、右ねじが進む向きが\(\vec{A}\times\vec{B}\)の向きです。
図2-2にこのことを表しました。
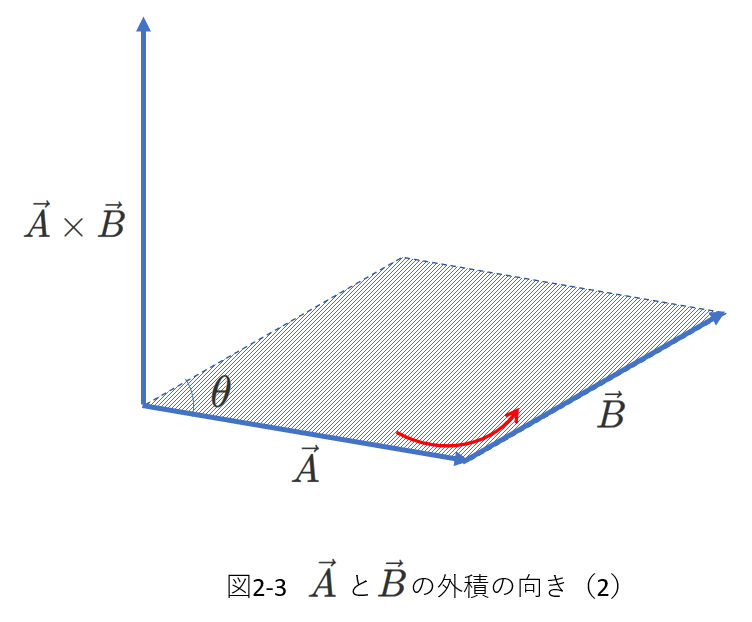
図2-3は、右ねじの法則を少し別の視点から説明しています。
\(\vec{A}\times\vec{B}\)の順番に合わせて、\(\vec{A}\)の終点に\(\vec{B}\)の始点を合わせます。
このとき、\(\vec{A}\)から見て、\(\vec{B}\)は左に向きを変えています。
この向きにねじを回したときねじが進む方向が\(\vec{A}\times\vec{B}\)の向きになります。
外積について説明しながら、ローレンツ力について考えます。
教科書には、荷電粒子が受けるローレンツ力の大きさ\(f\)は\(f=qvB\)と表されると書かれています。
\(q\)は荷電粒子が帯びている電荷量、\(v\)は荷電粒子の速度、\(B\)は磁場の強さです。
これを外積で表現すると、ローレンツ力の大きさも向きも一緒に表現できます。
\begin{equation} \vec{f}=q(\vec{v}\times\vec{B}) \tag{2-2} \end{equation}
\(q\)を除く量(速度と磁場)がベクトル表示に変わっていることに注意してください。
(2-2)式は、次のことを示しています。
・粒子の速度と磁場の角度が\(\theta\)であるとき、ローレンツ力の大きさは、
磁場に垂直な速度成分\(|\vec{v}|\sin\theta\)を考えて\(|\vec{f}|=|q||\vec{v}||\vec{B}|\sin\theta\)、
・ローレンツ力の向きはフレミングの左手の法則(あるいは、右ねじの法則)と、\(q\)の正負で決まります
外積とローレンツ力のポイントを示します。
1.\(\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}\) が成り立ちます。
つまり、交換法則 「\(\vec{A}\times\vec{B}=\vec{B}\times\vec{A}\)」 は成り立ちません。
図2-2で\(\vec{B}\times\vec{A}\)を考えてみましょう。
\(\vec{B}\times\vec{A}\)の向きは、\(\vec{B}\)から\(\vec{A}\)へ角度の小さい側を通って回そうとするときの右ねじの進む向きですから、\(\vec{A}\times\vec{B}\)とは逆になることがわかります。
つまり、\(\vec{A}\times\vec{B}\neq\vec{B}\times\vec{A}\)であり、\(\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}\) です。
さて、ここで大事なことは、
右ねじの法則と\(f=qvB\)の公式をそのまま覚えていれば、\(f\)の向きを知ることができます。
なんとなく\(q\)と\(v\)と\(B\)の積だということではなく、文字の順序も含めて\(f=qvB\)と覚えましょう。
実は、向きが伴う次の公式も外積で表現できます。
・電流が磁場から受ける力 \(F=IBl\) または、\(F=IBl\sin\theta\) は、
外積を使って、\(\vec{F}=(\vec{I}\times\vec{B}\ )\ l\)
・磁場を横切る導線に生じる誘導起電力 \(V=vBl\) または、\(V=vBl\sin\theta\) は、
外積を使って、\(\vec{V}=(\vec{v}\times\vec{B}\ )\ l\)
外積であらわされることと、公式を文字の順番まで正しく覚えていれば、
その向きは右ねじの法則から求めることができます。
また、どの場合も、ふたつのベクトルの向きが垂直ではなく、角度\(\theta\)の場合、\(\sin\theta\)を使って表されます。
2.\(\vec{A}\)と\(\vec{B}\)が平行なとき、\(\vec{A}\times\vec{B}\)は、\(\vec0\)(\(0\)ベクトル)です。
\(\vec{v}\)と\(\vec{B}\) が平行な場合(\(\sin\theta=0\)ですから)、\(q\vec{v}\vec{B}\) は\(\vec{0}\)です。
したがって、速度\(v\)と磁場\(B\)が平行な場合には、荷電粒子にローレンツ力ははたらきません。
3.\(\vec{A}\cdot(\vec{A}\times\vec{B})=0\)
内積は交換法則が成り立つので、\((\vec{A}\times\vec{B})\cdot\vec{A}=0\) とも書けます。
\((\vec{A}\times\vec{B})\) の向きは\(\vec{A}\)にも\(\vec{B}\)にも垂直です。
つまり、\(\vec{A}\)は、\((\vec{A}\times\vec{B})\)に垂直ですから、ふたつのベクトルの内積は\(0\)です。
(内積はスカラー量です)
ローレンツ力\(q\vec{v}\times\vec{B}\)は、\(\vec{v}\)と\(\vec{B}\)に垂直です。
円運動について考えます。
ローレンツ力は\(\vec{v}\)に垂直で、円運動の中心は向心力であるローレンツ力の向きにあります。
つまり、円運動の回転の軸の方向は、\(\vec{v}\) とローレンツ力に垂直ですから、\(\vec{B}\)の方向と一致します。
ローレンツ力\(\vec{F}\)がする仕事\(W\)について考えます。
\(\Delta t\)の間の物体の微小変位ベクトル\(\Delta\vec{x}\)を考えると、そのときの速度を\(\vec{v}\)として、\(\Delta\vec{x}=\vec{v}\Delta t\)ですから、
\begin{eqnarray} W=\vec{F}\cdot\Delta\vec{x}&=&(q\vec{v}\times\vec{B})\cdot\Delta\vec{x} \\
&=&(q\vec{v}\times\vec{B})\cdot\vec{v}\Delta t \\
&=&q\Delta t(\vec{v}\times\vec{B})\cdot\vec{v} \\
&=&0
\end{eqnarray}
ローレンツ力は仕事をしないことがわかります。
次に、ローレンツ力がはたらいている場合の小物体の運動を考えます。
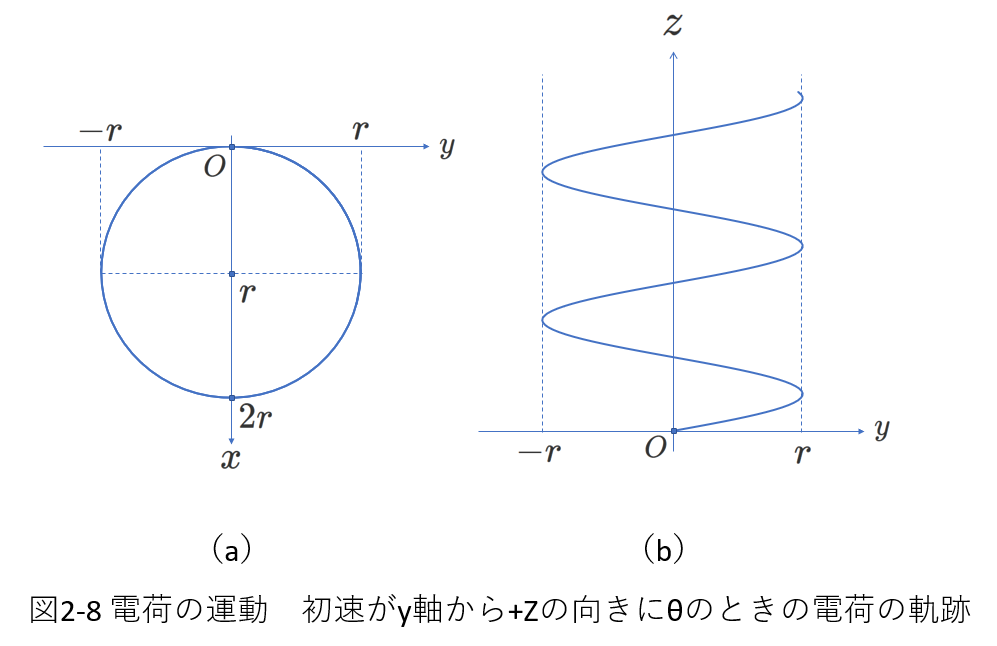
いくつかの例題を示しますが、磁場\(\vec{B}\)の向きは同じとし、電荷の進む向きを変えていきます。
最後に、磁場と共に電場がある場合を考察します。
例題(1)
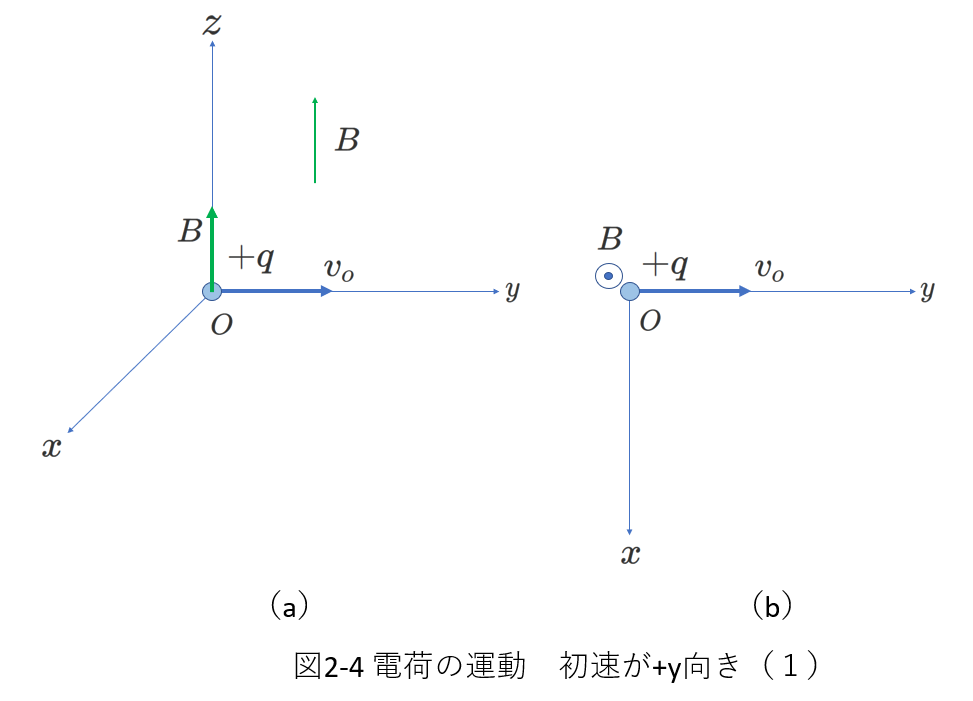
最初の例題を図2-4に示します。
(a)は3次元的に俯瞰した図、(b)は\(+z\)側から原点\(O\)の向きに眺めた図です。
磁場\(\vec{B}\)は一様(考察する領域内で、大きさも向きも場所に依存せずに一定)で、その向きは\(z\)方向の\(+z\)の向きで、\(+q(q\gt 0)\)の電気量を持つ小物体を原点\(O\)から初速\(v_0\)で\(+y\)向きに打ち出します。
そのときの小物体の軌跡を考察します。
このような問題では、小物体の質量は非常に小さいため重力の影響は無視できるとすることが多いので、ここでもそのように仮定します。
軌跡、つまり運動を調べるわけですから、最初にすることは小物体にはたらく力を考えます。
小物体にはたらく力は磁場から受けるローレンツ力だけです。
ローレンツ力の向きと大きさを求めます。
ローレンツ力がはたらく方向は、\(\vec{B}\)にも、\(\vec{v_0}\)にも垂直な方向です。
言い換えれば、\(\vec{B}\)と\(\vec{v_0}\)が決める平面に垂直な方向です。
このとき、\(\vec{B}\)ベクトルは、小物体の位置で考えてください。
一般的な問題では、図2-4(a)のように\(B\)の向きは小物体から離れた位置に示されているので注意してください。
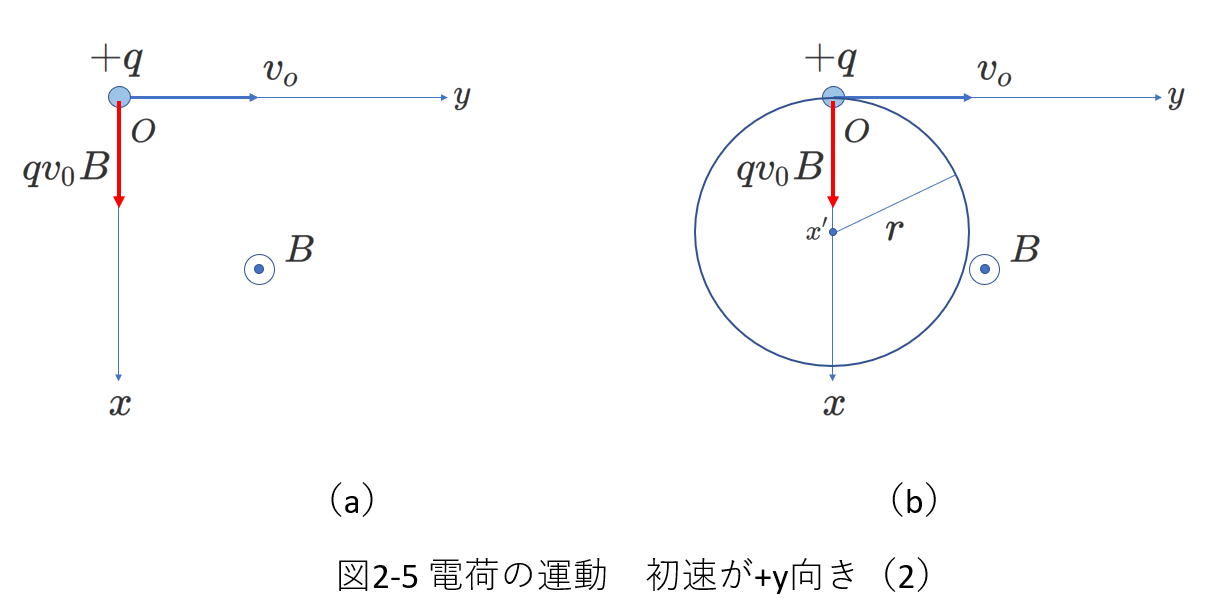
原点\(O\)でのローレンツ力の向きは、右ねじの法則を用いて、図2-5(a)のように\(+x\)向きであることがわかります。
(上の説明で、「方向」と「向き」の言葉の意味が異なることに注意してください。)
ローレンツ力は、\(\vec{B}\)の向きが変わらなくても物体の速度の向きが変わると、その向きが変わります。
原点\(O\)で小物体は\(+y\)向きで大きさ\(v_0\)の速度を持っていますが、\(+x\)向きにローレンツ力がはたらくために、\(+x\)の向きに速度が変化します。
このとき、ローレンツ力は小物体に対して仕事をしないので、速度の大きさ\(v_0\)は変化しません。
小物体は\(v_0\)の速さで等速円運動をすることがわかります。
ローレンツ力の大きさは、\(\vec{B}\)と\(\vec{v_0}\)が垂直であることから、\(qv_0B\)となります。
(\(v_0=|\vec{v_0}|\)、\(B=|\vec{B}|\) であるとします。)
円運動の中心軸(円運動の中心を通り、円運動をする平面に垂直な軸)が\(\vec{B}\)に平行になります。
この例題では、\(xy\)平面が\(\vec{B}\)に垂直な平面で、速度ベクトルも\(xy\)平面上にあるので、円運動は\(xy\)平面上で行われます。
円運動の半径と中心の座標を求めます。
円運動の半径は、運動方程式から求めます。
小物体の質量を\(m\)、円運動の半径を\(r\)とすると、円運動の運動方程式は、
\begin{eqnarray} m\frac{v_0^2}{r}&=&qv_0B \tag{2-3} \\
r&=&\frac{mv_0}{qB} \tag{2-4}
\end{eqnarray}
さて、円運動の中心を見つける上で重要なヒントは、
円運動の中心は向心力の向きにあるということです。
この円運動で向心力はローレンツ力ですから、円運動の中心はローレンツ力の向きにあるということです。
原点\(O\)でローレンツ力は\(+x\)の向きですから、円運動の中心は\(x\)軸上で、\(x\gt 0\)の領域にあることがわかります。
\(r\)を用いて表せば、円運動の中心の座標は\((r,0,0)\)であることがわかります。
小物体が円軌道を1回転する時間\(T\)は、[円周]÷[速さ]で求められます。
\begin{equation} T=\frac{2\pi r}{v_0}=\frac{2\pi m}{qB} \tag{2-5} \end{equation}
例題(2)
次に、初速度の向きを変えてみます。
図2-6(a)の図で、初速度\(v_0\)の向きは、前の例題同様\(xy\)平面に平行ですが、\(x\)軸\(y\)軸のいずれからも45°となる向きであるとします。
\(B\)の向きは前の例題と同じで\(+z\)の向き、\(+q\)に帯電した小物体の運動を考えます。
以後の例題では、ベクトル量であってもベクトルを表す矢印なしで記述することにします。
(\(\vec{B}\)を\(B\)と表現します)
ローレンツ力の方向は、\(B\)と\(v_0\)の両方に垂直な方向です。
\(B\)と\(v_0\)のベクトルが決める平面に垂直であるとも言えます。
向きは、右ねじの法則で求められます。
その大きさは、\(B\)と\(v_0\)の向きが垂直ですから、\(qv_0B\)となります。
前の例題と同じように、\(B\)の向きを回転軸とする円運動をすることがわかります。
(2-3)式と同じ円運動の運動方程式が立てられるので、円運動の半径は前の例題と同じです。
ただし、円運動の中心は異なります。
円運動の運動の中心は向心力の向きにあるということから、図2-6(b)の図を描くことができて、\(x'=\frac{r}{\sqrt{2}}\)、\(y'=-\frac{r}{\sqrt{2}}\) ですから、運動の中心の座標は\((\frac{r}{\sqrt{2}},-\frac{r}{\sqrt{2}},0)\)となります。
例題(3)
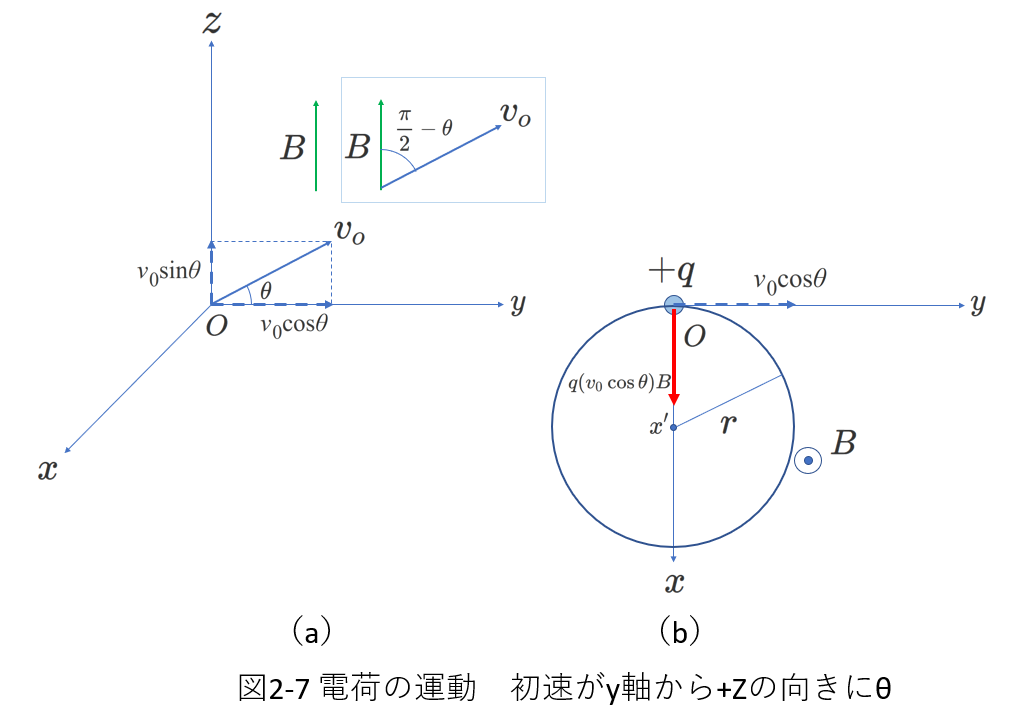
次に初速度の向きを\(+z\)の向きに傾かせてみます。
図2-7を参照してください。
前の例題と異なるのは、初速度に\(z\)成分が含まれることです。
図2-7(a)に示すように、初速度のベクトルは\(yz\)平面上にあり、\(+y\)向きから\(+z\)向きに角度\(\theta\)だけ傾いています。
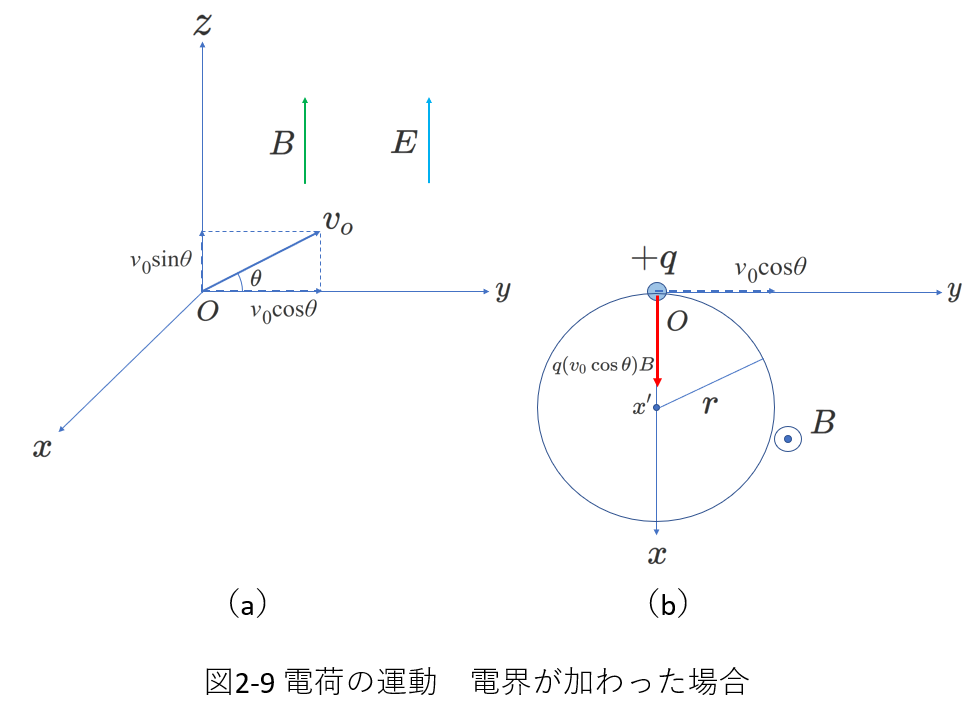
ローレンツ力の方向は、\(B\)と\(v_0\)の両方に垂直ですから、\(x\)軸方向です。
また、右ねじの法則から、ローレンツ力の向きは図2-7(b)に示すように、\(+x\)向きであることがわかります。
そして、ローレンツ力の大きさは\(q(v_0\cos\theta)B\)です。
外積の(2-1)式を見て、\(\cos\theta\)ではなく、\(\sin\theta\)ではないかと思うかもしれませんが、\(\theta\)がどこの角度を表すかを確認してください。
(2-1)式の中の\(\theta\)は、この例題では\(B\)と\(v_0\)の間の角度(\(\frac{\pi}{2}-\theta\))に対応します。
つまり、(2-1)式に従って、ローレンツ力の大きさを求めると、\(qv_0B\sin{\left(\frac{\pi}{2}-\theta\right)}=qv_0B\cos\theta\)となります。
もちろん、外積など意識せずに次のように考えれば良いです。
\(v_0\)は、磁場に垂直な成分\(v_0\cos\theta\)と磁場に平行な成分\(v_0\sin\theta\)に分解できます。
このうち、磁場に平行な成分は磁場から力を受けるようにははたらきません。
したがって、常に、速度の、磁場に垂直な成分を使ってローレンツ力を計算すれば良いことがわかります。
(この考えは、磁場の向きを基準にする場合です。速度の向きを基準にする場合には、磁場\(B\)の、速度に垂直な成分を用いて計算することになりますが、前述の「速度の、磁場に垂直な成分を使ってローレンツ力を計算する」方がわかりやすいと思います。)
つまり、荷電粒子の運動を考えるには、磁場に垂直な方向(磁場に垂直な平面に平行)な成分と、磁場の方向成分とに分けるとわかりやすいです。
図2-7(b)では、このうちの磁場に垂直な方向(磁場に垂直な平面に平行)な成分を考えています。
運動の軌跡を\(xy\)平面に正射影していると考えることもできます。
要するに、\(+z\)の領域から、\(-z\)の向きに運動を眺めたときの図が図2-7(b)です。
このとき、運動は円運動に見えます。
この円運動は、速さが\(v_0\cos\theta\)で向心力は\(q(v_0\cos\theta)B\)です。
したがって、円運動の方程式は、円運動の半径を\(r\)として、
\begin{eqnarray} m\frac{(v_0\cos\theta)^2}{r}&=&qv_0B\cos\theta \tag{2-6} \\
r&=&\frac{mv_0\cos\theta}{qB} \tag{2-7}
\end{eqnarray}
となります。
この式は、(2-4)式の\(v_0\)を\(v_0\cos\theta\)で置き換えれば得られます。
円運動の中心は向心力の向きにあることと、半径が(2-7)式の\(r\)で与えられるとして、その座標は、\((r,0)\)になります。
電荷は、\(xy\)平面にとどまっていないで、\(+z\)向きに運動しますから、\(x\)軸上の座標\(r\)の点を通って\(B\)に平行な直線を中心軸とする円運動(らせん運動)をしていることになります。
1周するのに要する時間\(T\)は、
\begin{eqnarray} T&=&\frac{2\pi r}{v_0\cos\theta} \tag{2-8} \\
&=&\frac{2\pi m}{qB} \tag{2-9}
\end{eqnarray}
注)(2-6)(2-8)式で\(\cos\theta\)を忘れやすいので気を付けましょう。
(2-9)式が、(2-5)式と同じであることは興味深いです。
つぎに、初速\(v_0\)の\(z\)方向成分\(v_0\sin\theta\)について考えます。
\(z\)方向は\(B\)に平行な方向ですから、ローレンツ力を考える必要はありません。
したがって、\(z\)方向には力がはたらかないのですから、この方向の運動は\(v_0\sin\theta\)の等速度運動です。
まとめると、\(B\)に垂直な面内での運動と、\(B\)に平行な方向の運動に分けて考えるのが常道です。
この例題では荷電粒子にはローレンツ力しかはたらきませんから、荷電粒子は仕事をされません。
つまり、運動エネルギーが変化することはなく、運動のどの時点でも同じ速さであると、わかります。
円運動が1周回る間に\(z\)方向に進む距離を計算します。
一周するのにかかる時間は(2-9)式、\(z\)方向の速さは\(v_0\sin\theta\)ですから、
\begin{equation} v_0\sin\theta\times T=v_0\sin\theta\times\frac{2\pi m}{qB}=\frac{2\pi mv_0\sin\theta}{qB} \end{equation}
となります。
次の図には、(a)運動の軌跡の\(xy\)平面への正射影と、(b)\(yz\)平面への正射影を示しました。
荷電粒子にはたらく重力は無視できるとしました。
この場合、荷電粒子にはたらく力は磁場によるローレンツ力だけです。
そして、ローレンツ力は仕事をしないわけですから、運動エネルギーは変化しません。
言い換えれば、運動のいずれの点でも、速さは同じです。
例題(4)
磁場に加えて、電場を導入します。
下図2-9(a)のように、\(B\)と同じ向きに電場\(E\)が加わりました。
電荷は\(E\)からも力を受けます。
この力の大きさは\(qE\)で、向きは\(q\gt 0\)ですから\(E\)の向きです。
\(E\)に垂直な方向(つまり、\(B\)に垂直な方向)には、電場からの力ははたらかないので、この方向には(3)と同じ議論ができることになります。
つまり、この場合の運動の\(xy\)平面への正射影は例題(3)と同じ円になります。
そして、\(z\)方向には、例題(3)の等速度運動とは異なり、\(E\)から受ける力による等加速度運動となります。
\(z\)方向の運動方程式は、この方向の加速度を\(a_z\)として、
\begin{eqnarray} ma_z&=&qE \tag{2-10} \\
a_z&=&\frac{qE}{m} \tag{2-11}
\end{eqnarray}
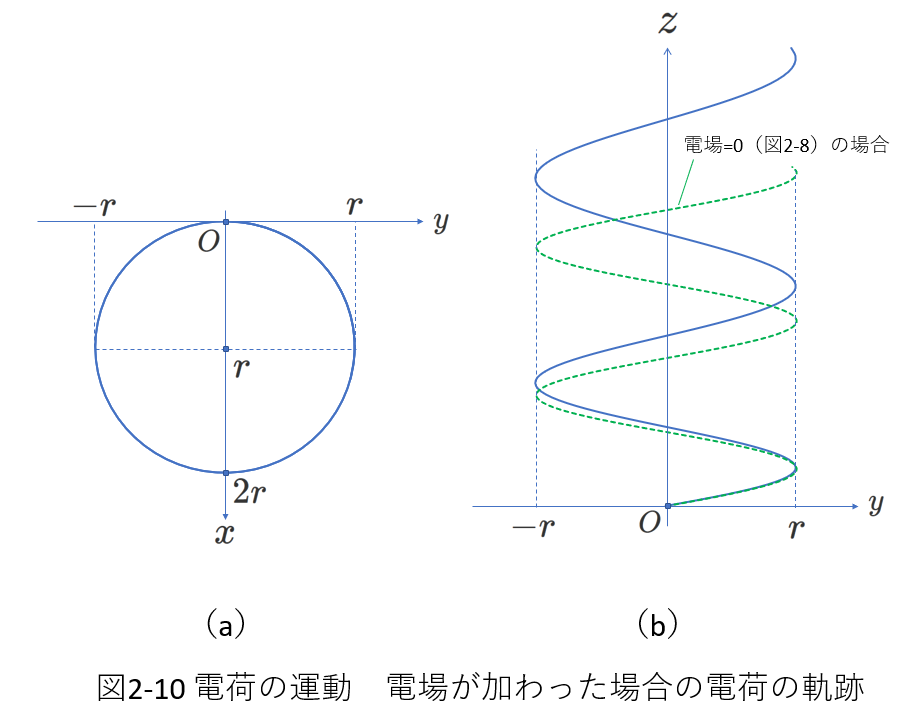
図2-10には、図2-8と同じように、運動の軌跡の\(xy\)平面上への正射影(a)と\(yz\)平面上への正射影(b)を示しました。
(b)では、例題(3)の場合を緑色の線で示しています。
これらを比較すると、青色の例題(4)の場合の運動では、加速度\(a_z\)により、1周回る間に\(z\)方向に進む距離が伸びていることがわかります。
速度の、\(xy\)平面に平行な方向の成分の大きさは例題(3)と変わらず、\(v_0\cos\theta\)ですから、円を1周する時間(周期)は例題(3)と同じです。
そして、\(z\)方向の速度成分の大きさ\(v_z\)は時間とともに増加します。
式で表せば、
\begin{equation} v_z=v_0\sin\theta+\frac{qE}{m}t \tag{2-12} \end{equation}
となります。
次に、原点\(O\)を出て、円運動を1周して\(z\)軸に達したときの速さ\(v_1\)を求めてみます。
A.
円を1周するのに要する時間\(t_1\)は、\(xy\)平面上への正射影で考えると、円周は\(2\pi r\)で、\(xy\)平面に平行な速度成分は\(v_0\cos\theta\)であることから、
\begin{eqnarray} t_1&=&\frac{2\pi r}{v_0\cos\theta} \\
&=&\frac{2\pi mv_0\cos\theta}{qBv_0\cos\theta} \\
&=&\frac{2\pi m}{qB}
\end{eqnarray}
B.
したがって、\(t_1\)での\(z\)方向の速さ\(v_{z1}\)は、(2-12)式を用いて、
\begin{eqnarray} v_{z1}&=&v_0\sin\theta+a_z\cdot t_1 \\
&=&v_0\sin\theta+\frac{qE\cdot 2\pi m}{m\cdot qB} \\
&=&v_0\sin\theta+\frac{2\pi E}{B}
\end{eqnarray}
C.
速さ\(v_1\)は、\(z\)方向の速度成分\(v_{z1}\)と平面\(xy\)に平行な速度成分\(v_0\cos\theta\)の合成により得られますから、
\begin{equation}
v_1=\sqrt{v_0^2\cos^2\theta+v_{z1}^2}
\end{equation}
として計算できます。
一様磁場中の荷電粒子の運動についてまとめます。
1.荷電粒子が磁場から受けるローレンツ力の向き
ローレンツ力の方向は、磁場と速度の両方に垂直な方向です。
向きは、速度ベクトルを磁場ベクトルに重ねる向きの右ねじの法則と電荷の正負からわかります。
2.ローレンツ力の大きさ
\(|q|\times (速度の、磁場Bに垂直な方向の成分)\times B\)
3.荷電粒子の円運動(1)
荷電粒子の速度が磁場方向の成分を持たない場合には、磁場に垂直な面内で円運動
磁場方向の速度を持つ場合は、磁場に垂直な面内での円運動と磁場方向の等速度運動の合成
⇒磁場に垂直な面内方向の運動と、磁場に平行な方向の運動に分けて考えます
4.荷電粒子の円運動(2)
円運動の半径は円運動の運動方程式から求めます
(運動方程式には、「速度の磁場に垂直な成分」を用います)
円運動の中心は、中心が向心力(ローレンツ力)の向きにあることと円運動の半径から求めます
1周回るのに要する時間は、「円運動の円周」÷「速さ」
(このときの速さも、「速度の磁場に垂直な成分」を用います)
5.ローレンツ力は仕事をしません
エネルギーの保存を考える場合には、この点に注意をします
Ⅲ.電場、電位、位置のエネルギー
静電気力、電場、電位、位置エネルギーに関連した公式をまとめています。
静電気力、電場、電位、位置エネルギーの式は形が良く似ているために、混同するミスが多いようです。
また、これらの式は、点電荷の場合と、一様な電場の場合に分けて考える必要があります。
1.点電荷の場合の静電気力、電場、電位、位置エネルギー
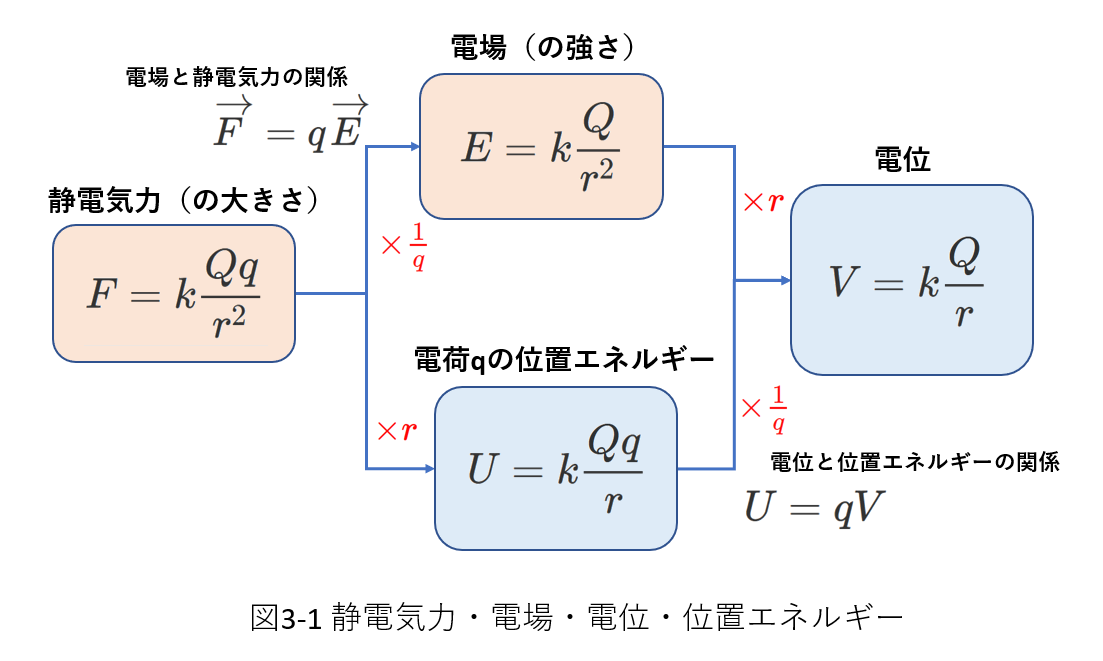
図3-1に、点電荷の場合について、静電気力・電場・電位・位置エネルギーの式をまとめました。
4つの式のうち、静電気力と電場はベクトル量です。
つまり、大きさと向きを持つため、図3-1では、それぞれ、「静電気力の大きさ」、「電場の強さ」というように、図3-1の\(F\)と\(E\)がベクトル量の絶対値を表していることを明確にする表現となっています。
一方、電位や位置エネルギーはスカラー量で大きさだけを持つため、「大きさ」や「強さ」という言葉を用いる必要はありません。
さて、出発点(基本)は静電気力の式です。
電荷\(Q\)と電荷\(q\)が及ぼし合う静電気力は、次のように表されます。
\begin{equation} F=k\frac{Qq}{r^2} \tag{3-1} \end{equation}
電場の大きさは、その位置に単位電荷(\(+1C\))があると仮定したときに、その電荷にはたらく力の大きさと定義されます。
また、電場の向きは静電気力の向きと同じです。
つまり、(3-1)式を\(q\)で割れば、\(Q\)の電荷がつくる電場の強さ\(E\)は次のように表されます。
\begin{equation} E=\frac{F}{q}=k\frac{Q}{r^2} \tag{3-2} \end{equation}
また、上述した内容から、
\begin{equation} \overrightarrow{F}=q\overrightarrow{E} \tag{3-3} \end{equation}
であることがわかります。
(3-3)式では、静電気力と電場の向きが同じであることを、ベクトルを使った表現で表しています。
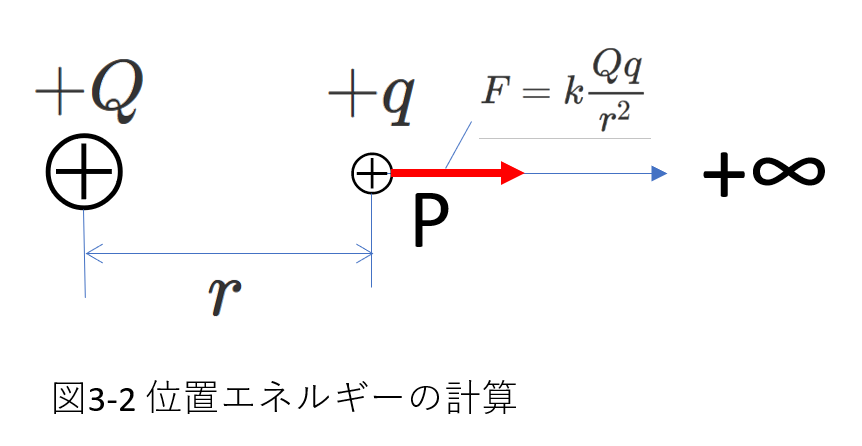
次に、位置エネルギーですが、電気量\(q\)を持つ物体をある点\(P\)から基準点まで動かしたときに静電気力がする仕事を、点\(P\)における物体の静電気力による位置エネルギーと言います。
点電荷の場合について、上の定義に沿って、
図3-2に示すように、点電荷\(+Q\)(\(\gt 0\))の作る電場中に\(r\)離れたところの点\(P\)にある電荷\(+q\)(\(\gt 0\))の静電気力による位置エネルギー\(U\)を計算します。
この状態で、\(+q\)は\(+Q\)から\(F=k\frac{Qq}{r^2}\)の大きさの静電気力を図の右向きに受けています。
\(+q\)が\(r\)から\(r+\Delta r\)動いたときに静電気力がした仕事は、\(F\Delta r\)です。
位置エネルギーの基準を\(+\infty\)として、\(F\Delta r\)を\(r\)から\(+\infty\)まで足し合わせるということは、\(F\)を\(r\)から\(+\infty\)まで積分するということですから、
\begin{eqnarray} U&=&\int_r^\infty F\Delta r \\
&=&\int_r^\infty k\frac{Qq}{r^2}\Delta r \\
&=&kQq\int_r^\infty r^{-2} \Delta r \\
&=&kQq\left[-\frac{1}{r}\right]_r^\infty \\
&=&k\frac{Qq}{r} \tag{3-4}
\end{eqnarray}
となります。
図3-1で、静電気力から電荷\(q\)の位置エネルギーの向かう矢印に\(\times r\)と書かれていますが、これは式がそのように変形されているように見えるということで、物理的な意味を反映しているものではありません。
(3-4)式で説明したように、物理的な意味は積分を施すということです。
(このことは、電場から電位に向かう\(\times r\)でも同じです。)
電荷\(1C\)当たりの静電気力による位置エネルギーが電位ですから、電位\(V\)は、次のようになります。
\begin{equation} V=\frac{U}{q}=k\frac{Q}{r} \tag{3-5} \end{equation}
そして、[静電気力による位置エネルギー]=[電荷]×[電位]
\begin{equation} U=qV \tag{3-6} \end{equation}
です。
万有引力による位置エネルギーは、\(U=G\frac{Mm}{r}\)と表されます。
これは、点電荷の場合の静電気力による位置エネルギーの式(3-4)と同じ形です。
「万有引力の大きさ」と「静電気力の大きさ」の式も同じ形をしていますが、「万有引力」には「電位」に相当するものがありません。
これは私の考えで(間違っているかもしれませんが)、質量\(m\)は変化しないのに対して、電荷\(q\)は変化するため、「電位」という概念が生まれたものと思います。
実際、「電荷」と「電位」を切り分けて考えることで、考察が非常に容易になります。
2.一様な電場の場合の静電気力、電場、電位、位置エネルギー
コンデンサーの両極板間には、ほぼ一様な電場が存在します。
コンデンサーの状態として、極板の電荷\(Q\)がわかっている場合と、極板間の電位差\(V\)がわかっている場合にわけて考えます。
\(Q\)と\(V\)はコンデンサーの電気容量\(C\)によって \(Q=CV\) と関連付けられますから、分けて考える必要はないのですが、ここでは両方の場合を考えます。
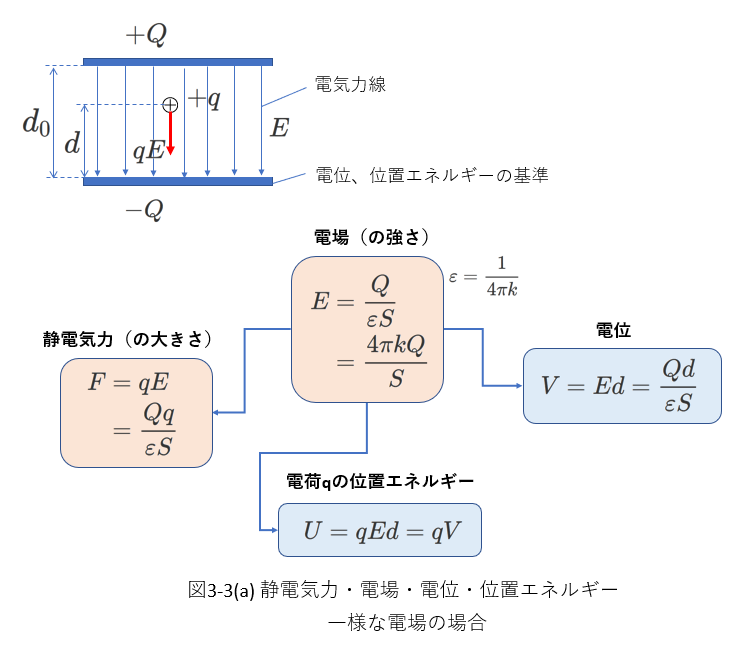
図3-3(a)の左上にコンデンサーの状態を示しました。
極板間距離が\(d_0\)、極板面積\(S\)のコンデンサーの極板に\(Q\)の電荷が蓄積されています。
その電荷により、極板間にほぼ一様な電場(強さが\(E\))が形成されています。
この電場中に\(+q\)の電荷を置いたとき、電荷\(q\)にはたらく力、位置エネルギー、電位を表す式を図3-3(a)に示します。
ここで、位置エネルギーと電位の基準を、コンデンサーの負側の極板としています。
コンデンサーに\(Q\)の電荷が蓄積されているときの電場の強さ\(E\)は、\(E=\frac{Q}{\varepsilon S}\)と計算できます。
この式は「ガウスの法則」から導かれます。
「ガウスの法則」
\(Q[C]\)の電荷をもつ物体から出ていく電気力線の総数は\(4\pi kQ\)である。
というものです。
そして、電気力線の密度が電場の強さを表します。
図3-3(a)のコンデンサーの図で、電気力線は\(+\)側極板から\(-\)側極板に向かっています。
それ以外の方向には電気力線はありません。
つまり、\(+\)側極板から出るすべての電気力線は、極板間の極板に平行な面(面積\(S\))を垂直に貫通します。
電気力線の密度は\(S\)の内部であれば一定です。
極板間の電場の強さを\(E\)とすると、電気力線の本数は\(ES\)と表されます。
一方で、ガウスの法則からは、電気力線の本数は\(4\pi kQ\)となります。
したがって、
\begin{eqnarray} ES&=&4\pi kQ \\
E&=&\frac{4\pi kQ}{S}=\frac{Q}{\varepsilon S} \tag{3-7} \\
ここで、\varepsilon&=&\frac{1}{4\pi k} \tag{3-8}
\end{eqnarray}
(3-7)で大事な点は、コンデンサーの極板間の電場の強さ\(E\)は、\(Q\)が一定であれば、極板間隔\(d_0\)に依存しないということです。
これは、仮に\(d_0\)が変化するように極板を(極板の面に垂直な方向に)動かしても、電気力線の本数が変化しないことからもわかります。
(3-3)式はこの場合にも成り立って、電場の強さ\(E\)の中に電荷\(q\)(\(\gt 0\))を置けば、その電荷にはたらく力\(F\)は、\(F=qE\)と表されます。
この電荷が\(-\)側極板から、\(d\)の距離離れた位置にあって、\(-\)側極板まで動かすときに静電気力がする仕事は\(qEd\)です。
したがって、\(-\)側極板から\(d\)の距離離れた電荷\(q\)は\(-\)側極板にあるときよりも\(U=qEd\)だけ位置のエネルギーが高いということになります。
電荷が\(1[C]\)のときの位置エネルギーが電位\(V\)ですから\(V=Ed\)です。
以上のことを整理すると、
\begin{eqnarray} \overrightarrow{F}&=&q\overrightarrow{E} \tag{3-3} \\
U&=&qEd=qV \tag{3-9} \\
V&=&Ed \tag{3-10}
\end{eqnarray}
上の式では、電荷\(q\)が極板間に極板から離れて存在する場合を考えました。
これは、一様電場の中を電荷が運動するというような場合に対応します。
コンデンサーの極板間の電位差\(V\)は、\(d=d_0\)として、\(V=Ed_0 \tag{3-11} \)と表されます。
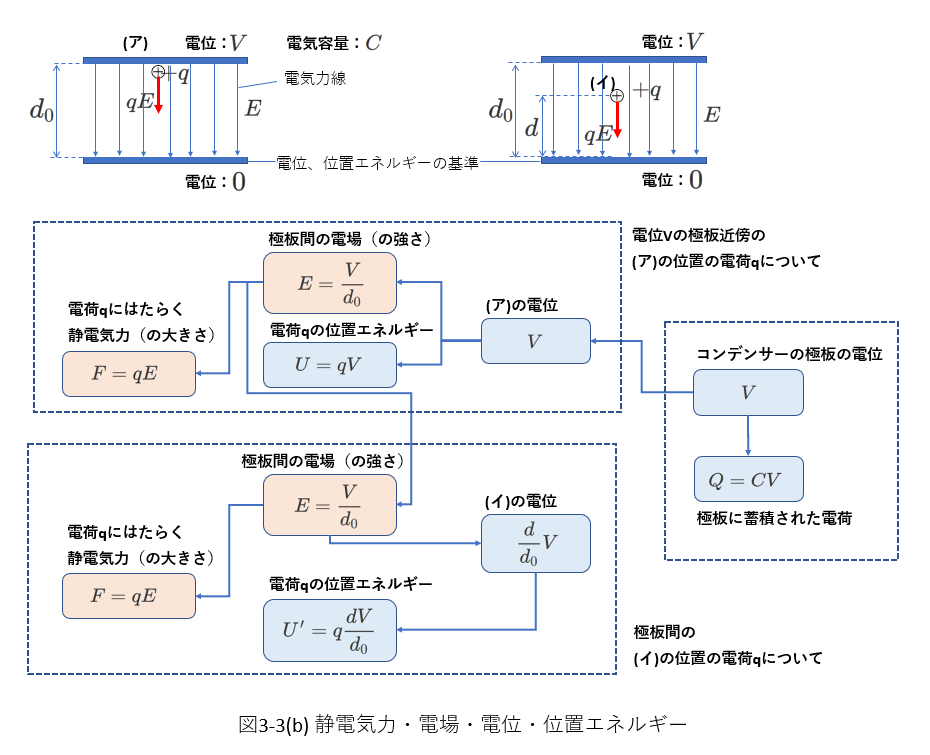
次に、極板間の電位差\(V\)が与えられたときの、電場の強さや電荷\(q\)が受ける力の大きさ、その位置エネルギーについて、図3-3(b)にまとめました。
コンデンサーの極板間に電位差\(V\)を与えたとき、極板間には一様な電場が形成されます。
一様な電場とは、考えている範囲(ここでは、極板間)では、どこでもその大きさと向きが同じである電場をいいます。
この電場の強さは、(3-11)式から、\(E=\frac{V}{d_0} \tag{3-12} \)となります。
図3-3(b)では、電荷\(q\)が電位\(V\)の極板の近傍にある(ア)の場合と、極板の間にある(イ)の場合のそれぞれについて、その電位と位置エネルギー、受ける力が示されています。
電位は電場の中の位置によって決まります。
極板と同じ位置にある(ア)の場合には、電荷\(q\)の電位は極板と同じ\(V\)です。
極板の間にある(イ)の場合は、電位\(0\)の極板からの距離を\(d\)として、その電位は\(\frac{d}{d_0}V\)と表されます。
(ア)の場合で注意するのは、このときの電荷\(q\)は、電位差\(V\)によって極板に蓄積された電荷とは違うものであることです。
電荷\(q\)は、あくまでも、外から電場中に置かれたものです。
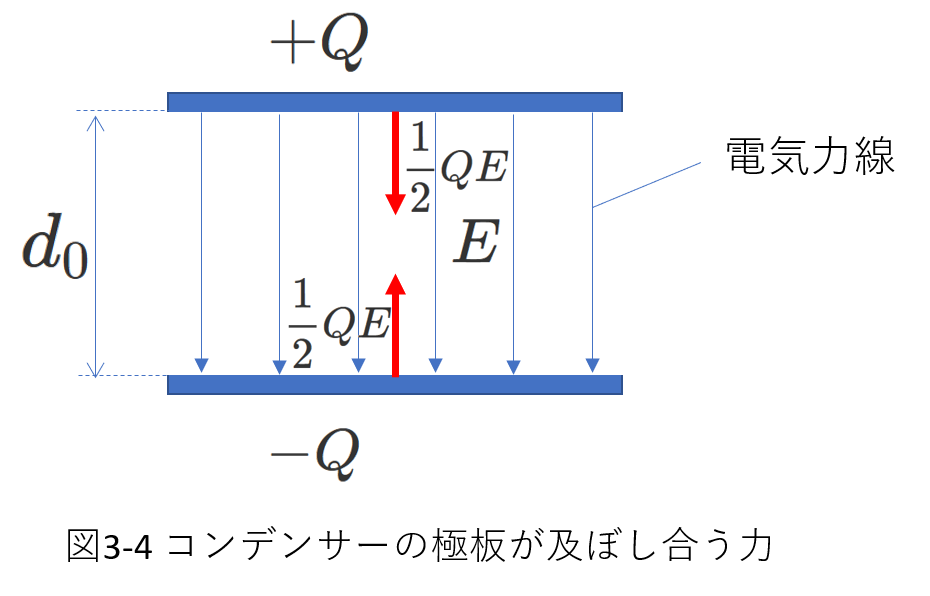
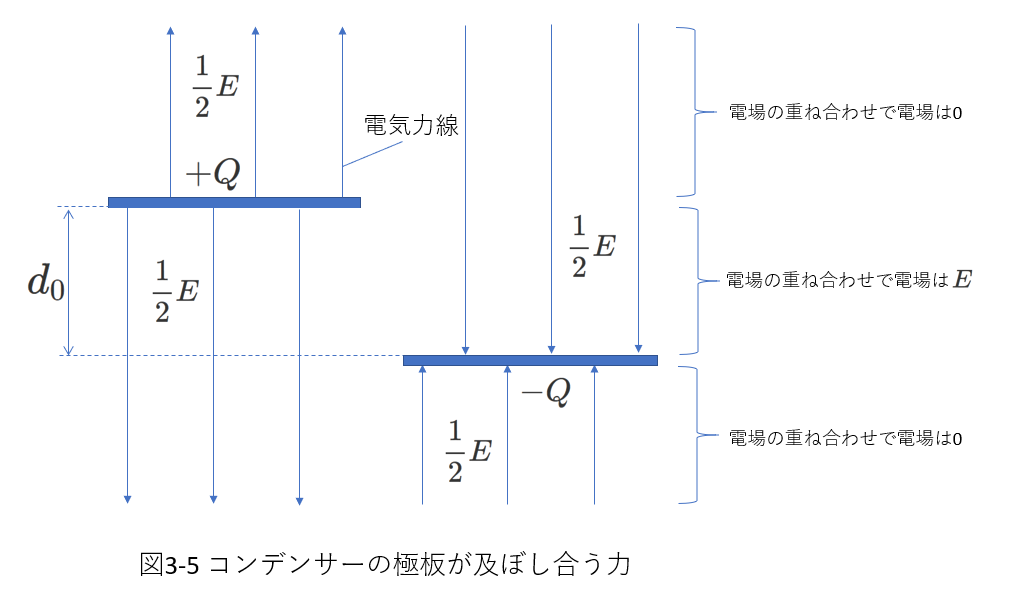
よく出される問題に、コンデンサーの2つの極板が及ぼし合う力を求めるものがあります。
これは、言い換えれば、両極板の正負の電荷が及ぼし合う静電気力を求める問題で、図3-4のような場合です。
\(+Q\)の電荷が蓄えられている極板と\(-Q\)が蓄えられている極板には、それぞれ、引き合う向きの静電力がはたらきます。
電場の強さが\(E\)で極場の電荷が\(Q\)であることから、この力の大きさ\(F\)を\(QE\)と答えたくなりますが、これは誤りです。
正しくは、\(F=\frac{1}{2}QE \tag{3-13} \) です。
図3-3のコンデンサーの極板間に電荷\(q\)がある場合と、図3-4では状況が異なりことがわかりますか。
図3-3では、コンデンサーの電荷\(+Q\)と\(-Q\)が作る電場の中に別の電荷\(+q\)を置き、これが受ける力を求めています。
一方、図3-4では、\(+Q\)または\(-Q\)が受ける力を求めるのですが、\(+Q\)および\(-Q\)は極板間の電場を作る役目もしています。
このことから、このときの電場の強さを単純に\(QE\)とすることには問題がありそうだと感じることができると良いです。
(3-13)式の\(\frac{1}{2}\)の意味を理解するために、図3-5を用意しました。
コンデンサーの極板を二つに分けて、それぞれの電荷が作る電場を表したものです。
極板を左右にずらして描いてありますが、これは、それぞれの極板が単独で存在している場合の電気力線を描いた図と考えてください。
図3-5の左側の図において、同じ空間内には負の電荷が存在してしないので、極板の対称性を考えれば、電気力線は極板の両側から出て、無限遠まで伸びます。
(極板の端では電気力線が乱れますが、ここではそれを無視しています。)
さて、ガウスの法則によれば、同じ量の電荷から出入りする電気力線の数は同じです。
両側に出ることは、片側だけに出るときと比べて、電気力線の密度が\(\frac{1}{2}\)になることになり、電場の強さは\(\frac{1}{2}E\)となります。
図3-5から、図3-3のコンデンサーの図を導くには、電場の重ね合わせを用います。
つまり、コンデンサーの周りの電場は、\(+Q\)が帯電した\(+\)側極板だけが存在する場合の電場と、\(-Q\)が帯電した\(-\)側極板だけが存在する場合の電場を合成することで得られます。
電場はベクトル量ですから、合成もベクトルとして計算をします。
極板間の空間では、向きが同じで、強さ\(\frac{1}{2}E\)のふたつの電場が合成されるので、電場の強さは\(E\)となります。
一方、極板の外側の空間では、向きが異なるふたつの電場(強さ、\(\frac{1}{2}E\))が合成されるので、電場の強さは\(0\)です。
また、図3-5の右側の図のように、\(-Q\)の作る電場は極板に対して対称です。
したがって、\(-Q\)の電荷は自分自身がつくる電場からは力を受けません。
以上のことから、コンデンサーの\(-\)側極板の電荷\(-Q\)が受ける力は、\(+\)側極板の\(+Q\)の電荷が作る、大きさ\(\frac{1}{2}E\)の電場の中に\(-Q\)の電荷を置いたときに、\(-Q\)が受ける力として計算できます。
また、コンデンサーの\(+\)側極板の電荷\(+Q\)が受ける力は、\(-\)側極板の\(-Q\)の電荷が作る、大きさ\(\frac{1}{2}E\)の電場の中に\(+Q\)の電荷を置いたときに、\(+Q\)が受ける力として計算できます。
いずれも力の大きさは、\(\frac{1}{2}QE\)となります。
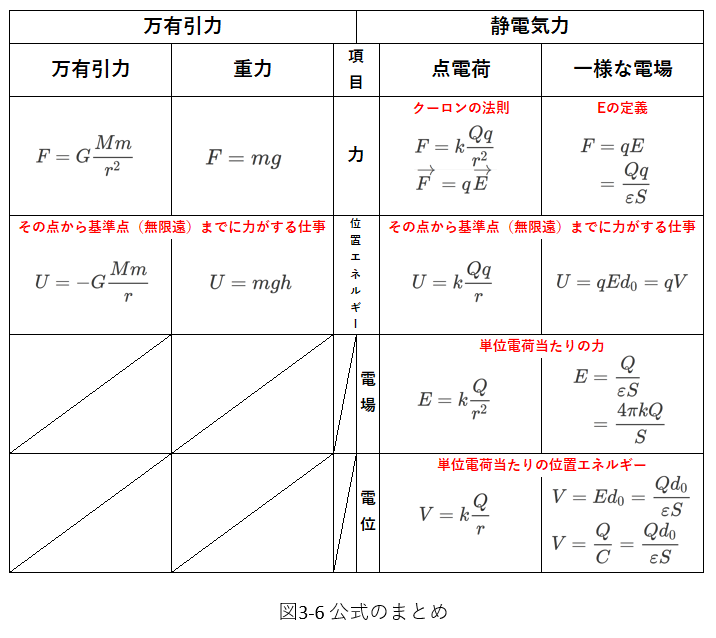
3.公式のまとめ
これまでの公式を、万有引力や重力の公式と比較しながら、まとめます。
これまでに示した静電気力に関連した公式を、万有引力に関する公式と並べて表(図3-6)にしました。
静電気力は「点電荷の場合」と「一様な電場」にわけて示し、それに対応して、万有引力は「万有引力」と「重力」にわけて示しています。
点電荷が及ぼし合う静電気力は、万有引力(たとえば地球と人工衛星の間にはたらく力)の式と形が同じです。
したがって、それぞれの位置エネルギーの式も同じ形になっています。
質量が正の値であるのに対して、電荷は正負両方の値を取り得ます。
つまり、万有引力は引力だけですが、静電気力は引力と斥力の両方の場合があります。
これが、静電気力と万有引力の違いです。
これらの位置エネルギーは、普通、「無限遠」を基準「\(0\)」とします。
このとき、万有引力の位置エネルギーは常に負ですが、静電気力の位置エネルギーは電荷の正負に応じて、正負両方の値を取り得ます。
図3-6の位置エネルギーの欄に示されているように、位置のエネルギーは、「その点から基準点までに力がする仕事」です。
位置のエネルギーが「正」であるということは、その点から基準点に向かう向きと力(万有引力でも、静電気力でも)がその向きに向いているわけですから、外力を加えなくても、手を放せば、物体はその点から基準点に移動するということです。
このとき、その点の位置のエネルギーは正、基準点は\(0\)となります。
つまり、物体は万有引力または、静電気力の力以外の力がはたらいていないときには、位置エネルギーの高い点から低い点に移動し、このとき、位置のエネルギーの一部が運動エネルギーに変わり、物体の速さが増加します。
(手に持った荷物の手を放せば、地面に落ちます。位置エネルギーの高い「手の位置」から低い「地面」に物体が移動しました。)
このように、どちらの点の位置エネルギーが高いか低いかを考えるには、手を離したときに、物体がどちらに向かうかを調べると良いです。
繰り返しになりますはが、図3-2の状態で、\(+q\)の電荷を固定していなければ、\(+Q\)との斥力で右向きに力を受け、加速し、運動エネルギーが増加します。
つまり、図3-2において、\(+q\)の位置エネルギーは\(+Q\)に近いほど高く、離れるほど低くなります。
無限遠を位置のエネルギーが\(0\)の基準にとると、\(+q\)の電荷は図の位置で正の位置のエネルギーを持っていることになります。
静電気力の場合には、「電場」や「電位」を考えることも、万有引力との違いです。
それぞれ、「単位電荷当たりの力」「単位電荷当たりの位置のエネルギー」を意味します。
電気回路では、コンデンサーに蓄えられる電荷や回路を移動する電荷は(時間により)変化します。。
したがって、電荷\(q\)と電位\(V\)を分けて考える必要があることから、「電位」を考えたものと思います。
(私の個人的な想像です。)
次に、「重力」と「一様な電場」を比較します。
この場合も、力と位置のエネルギーの式が似た形になることがわかります。
仮に、一様な電場\(E\)の中に電荷\(q\)に帯電した質量\(m\)の物体を置くと、物体にはたらく力は\(qE\)ですから、加速度を\(\alpha\)として、運動方程式は、\(m\alpha=qE \tag{3-14} \)となります。
したがって、\(\alpha=\frac{qE}{m} \tag{3-15} \)です。
この式から、加速度\(\alpha\)は一定であることがわかりますから、物体の運動は加速度\(\frac{qE}{m}\)の等加速度運動です。
つまり、加速度の大きさは異なりますが、重力を受ける物体と同様の運動をします。
一様な電界中の電荷の運動というと難しく思われますが、重力の場合と同じように考えることができるということです。
4.例題
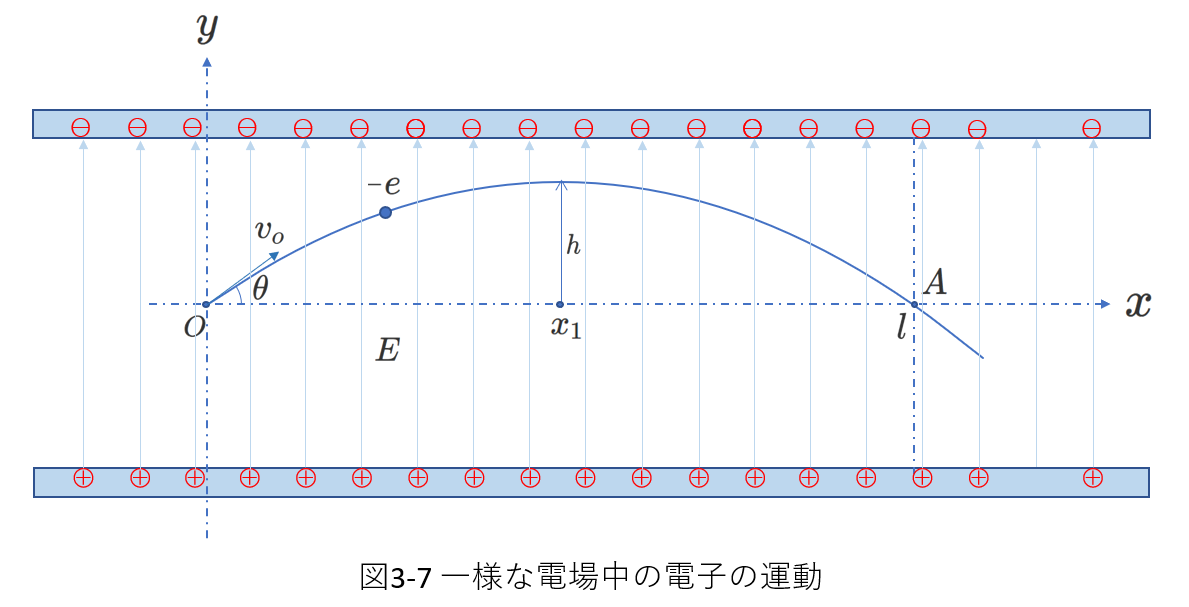
一様な電場中での電子の運動を考えます。
右図3-7のように、強さ\(E\)で\(+y\)向きの一様な電場が作られています。
一様な電場は、コンデンサーのように、電荷が蓄えられた2枚の極板を向かい合わせに置くことでつくられています、。 極板の面積が大きく、間隔が狭いほど一様な電場とみなせます。)
2枚の極板は、画面に垂直に、お互いに平行になるように配置され、図3-7は、その断面を示しています。
\(x\)軸と\(y\)軸が図のように、それぞれ、水平方向、鉛直方向に設定されています。
この図で、電荷\(-e\)(\(e\gt 0\))で質量\(m\)の電子が点\(O\)において、大きさが\(v_0\)で、\(x\)軸との角度が\(\theta\)の向きの速度を持っています。
重力の影響は小さく無視できるものとして、電子の最大到達点\(h\)と、\(x=l\)の点で\(x\)軸と交差するための、\(v_0\)と\(\theta\)の条件を求めます。
運動を調べるのですから、運動方程式を立てます。
そして、その前に、電子にはたらく力を考察します。
重力は無視できるとしていますから、電子が受ける力は電場から受ける静電気力だけです。
その大きさは\(eE\)で、向きは電子の電荷が負(\(-e \lt 0\))ですから、電場と逆向き(すなわち、\(-y\)向き)にはたらきます。
電子の加速度の\(x\)成分を\(\alpha_x\)、\(y\)成分を\(\alpha_y\)、それぞれの正の向きを\(+x\)向き、\(+y\)向きとして、運動方程式を立てます。
\begin{eqnarray} m\alpha_x&=&0 \tag{3-16} \\
m\alpha_y&=&-eE \tag{3-17} \\
これより、&& \\
\alpha_x&=&0 \tag{3-18} \\
\alpha_y&=&-\frac{eE}{m} \tag{3-19}
\end{eqnarray}
これより、\(x\)方向には等速度運動、\(y\)方向には等加速度運動をしていることがわかります。
\(x\)方向には、\(v_0\cos\theta\)の速さで等速度運動、\(y\)方向には\(\alpha_y=-\frac{eE}{m}\)の等加速度運動をします。
つまり、斜め上にボールを投げ上げたときのボールの運動と同様の運動をすることになります。
1.\(h\)を求めます
\(h\)を求めるのにはいろいろな考え方があります。
最初は、一度に\(h\)を求める方法です。
① \(y\)方向には等加速度運動をしているので、「等加速度運動の式」を用います。
加速度\(\alpha_y\)のもとで\(h\)変位したときに、\(y\)方向の速さが\(v_0\sin\theta\)から\(0\)に変化したので、
\begin{equation} 0^2-(v_0\sin\theta)^2=2\times\alpha_y\times h \tag{3-20} \end{equation}
この方法が最も簡便に\(h\)を求めることができます。
② 「仕事」と「運動エネルギーの変化量」の関係の式を用います。
電磁力が電子にした仕事は、\(-eEh\)です。
電子の進む向きと力の向きが逆ですから、仕事は負になることに注意します。
この仕事により、電子の運動エネルギーが\(\frac{1}{2}mv_0^2\)から\(\frac{1}{2}m(v_0\cos\theta)^2\)に変化します。
最高点での電子の速度は、水平右向きに\(v_0\cos\theta\)(\(0\)ではありません)であることに注意しましょう。
\begin{equation} \frac{1}{2}m(v_0\cos\theta)^2-\frac{1}{2}mv_0^2=-eEh \tag{3-21} \end{equation}
③ 電磁気力の位置エネルギーを考慮してエネルギー保存の式を立てます。
位置エネルギーはその点から基準点までに電磁力がした仕事です。
点\(O\)から最高点に達するまでに、電磁力がした仕事は\(-eEh\)ですから、点\(O\)での位置エネルギーは最高点を基準(位置エネルギーが\(0\))として、\(-eEh\)であることになります。
したがって、電子の持つエネルギーが保存されることを表す式は、[点\(O\)での電子のエネルギー]=[最高点での電子のエネルギー]の形で次のようにあらわされます。
\begin{equation} \frac{1}{2}mv_0^2+\left(-eEh\right)=\frac{1}{2}m(v_0\cos\theta)^2+0 \tag{3-22} \end{equation}
④ 電子の軌跡を式で表し、その式の形から最高点の高さを求めます。
電子が点\(O\)にあるときの時刻を\(0\)とします。
このとき、時刻\(t\)の時の電子の\(x\)座標と\(y\)座標は次のようにあらわされます。
\begin{eqnarray} x&=&v_0\cos\theta\times t \tag{3-23} \\
y&=&v_0\sin\theta\times t+\frac{1}{2}\alpha_y t^2 \tag{3-24}
\end{eqnarray}
(3-24)式を平方完成すれば、\(y\)の最大値がわかります。
\begin{eqnarray} y&=&\frac{1}{2}\alpha_y\left(t+\frac{v_0\sin\theta}{\alpha_y}\right)^2-\frac{1}{2}\alpha_y\left (\frac{v_0\sin\theta}{\alpha_y}\right)^2 \\
&=&\frac{1}{2}\alpha_y\left(t+\frac{v_0\sin\theta}{\alpha_y}\right)^2-\frac{(v_0\sin\theta)^2}{2\alpha_y} \tag{3-25}
\end{eqnarray}
\(t=-\frac{v_0\sin\theta}{\alpha_y}\)のとき、\(y\)が最大となり、\(y=-\frac{v_0\sin\theta)^2}{2\alpha_y}\)です。
これらの式に負号がついているのは、(3-19)式からわかるように\(\alpha_y\)が負であるためです。
(3-23)(3-24)式から\(t\)を消去すれば、\(y\)は\(x\)の二乗の式で表されます。
この式を平方完成しても、\(h\)を求めることができますが、(3-25)式のように(3-24)式だけからでも\(h\)を求めることができるわけですから、(3-24)式を使うのが普通です。
(3-20)(3-21)(3-22)式はよく似ています。
特に、(3-21)式と(3-22)式は項の位置が異なるだけです。
その式の形から、その式を立式した根拠がわかることを確認してください。
(3-21)式は、[運動エネルギーの変化量]=[仕事]を表しているわけですが、(3-22)式のエネルギー保存の式が変形され、[運動エネルギーの増加量]=[位置エネルギーの減少量]を表していると考えることもできます。
ですが、エネルギー保存の式は、(3-22)のように[ある時刻のエネルギーの総和]=[別の時刻のエネルギーの総和]という表現にするのが、最もミスが少なく立式できます。
それは、形式的に各エネルギーの値を求め、それらを右辺と左辺に分けて足し合わせれば良いからです。
注) 運動エネルギーはスカラー量であって、\(x\)成分、\(y\)成分に分けられるわけではありません。
(3-20)式の両辺に質量\(m\)を掛け、\(2\)で割れば、
\begin{equation} \frac{1}{2}m\times 0^2-\frac{1}{2}m(v_0\sin\theta)^2=-eEh \tag{3-26} \end{equation}
という式が得られます。
この式を運動エネルギーの\(y\)方向成分について成り立つ式と考えてはいけません。
運動エネルギーはベクトル量の速度を用いて計算しますが、その結果の運動エネルギーはスカラー量であって、運動エネルギーを\(x\)成分、\(y\)成分に分けられるわけではありません。
この例題において、\(x\)方向の加速度は\(0\)で、電子が点\(O\)から最高点に達するまでに、\(x\)方向の速度は\(v_0\cos\theta\)から\(v_0\cos\theta\)に変化する(つまり、変化しない)ことから、(3-20)式に相当する「等加速度運動の式」は次のようになります。
\begin{equation} (v_0\cos\theta)^2-(v_0\cos\theta)^2=2\times 0\times l \tag{3-27} \end{equation}
両辺を\(2\)で割り、質量\(m\)を掛ければ、
\begin{equation} \frac{1}{2}m (v_0\cos\theta)^2-\frac{1}{2}m(v_0\cos\theta)^2=0 \tag{3-28} \end{equation}
このように書けるわけですが、これも、運動エネルギーの\(x\)成分について成り立つ式ではありません。
(3-26)式と(3-28)式の各辺を足し合わせると、
\begin{eqnarray} \frac{1}{2}m (v_0\cos\theta)^2-\frac{1}{2}m{((v_0\sin\theta)^2+v_0\cos\theta)^2}&=&-eEh \tag{3-29} \\
\frac{1}{2}m (v_0\cos\theta)^2-\frac{1}{2}mv_0^2&=&-eEh \tag{3-30}
\end{eqnarray}
(3-30)式は(3-22)式と等しくなりました。
しかし、(3-26)式と(3-28)式が運動エネルギーの\(y\)方向成分、\(x\)方向成分それぞれのエネルギーの保存を表しているわけではありません。
⑤ さて、電子が最高点に達する時刻\(t=t_1\)が分かれば、(3-24)式を使って\(h\)を求めることができます。
ただ\(h\)を求めるだけであれば、①②③の方法を用いるのが楽ですが、最高点に達する時刻が必要な場合には、次のような方法を使います。
⑤-1 最高点の時刻を求めるには、「最高点で速度の\(y\)方向成分が\(0\)になる」ことを使います。
\(y\)方向の速度\(v_y\)は、
\begin{equation} v_y=v_0\sin\theta+\alpha_y\times t \tag{3-31} \end{equation}
(3-31)式で\(v_y=0\)とすれば、\(t_1\)が求められます。
⑤-2 また、力積と運動量の変化量の関係を表す式からも\(t_1\)を求めることができます。
電子が点\(O\)から最高点に到達する間、一定の大きさ\(eE\)の静電気力が\(-y\)向きに\(t_1\)の時間はたらいているので、電子が受ける力積は、大きさが\(eEt_1\)で\(-y\)向きです。
これにより\(y\)方向の運動量が、\(mv_0\sin\theta\)から\(0\)に変化します。以上より、
\begin{equation} 0-mv_0\sin\theta=-eEt_1 \tag{3-32} \end{equation}
これより、\(t_1\)を求めることができます。
⑤-3 また、それ以前に、(3-24)式を平方完成した(3-25)でも\(t_1\)を求めることができています。
2.電子が点\(A\)(\(l\),\(0\))を通るための、\(v_0\)と\(\theta\)の条件を求めます。
⑥ 等加速度運動の対称性から、電子が点\(O\)から点\(A\)に至る時間\(t_2\)は、点\(O\)から最高点に達する時間\(t_1\)の2倍になります。
そこで、(3-23)式に、\(x=l\)と\(t=2t_1\)を代入します。(3-25)式から、\(t_1=-\frac{v_0\sin\theta}{\alpha_y}\) ですから、
\begin{eqnarray} l&=&v_0\cos\theta\times 2t_1 \\
l&=&-\frac{2v_0^2\cos\theta\sin\theta}{\alpha_y} \tag{3-33} \\
(3-19)式の\alpha_yを代入して、eEl&=&2mv_0^2\cos\theta\sin\theta \tag{3-34}
\end{eqnarray}
(3-24)式を使ってもできそうな気がしますね。
(3-24)式で、\(y=0\)と\(t=2t_1\)を代入します。
\begin{eqnarray} 0&=&v_0\sin\theta\times 2t_1+\frac{1}{2}\alpha_y\times (2t_1)^2 \tag{3-35} \\
t_1\neq 0ですから、0&=&v_0\sin\theta+\frac{1}{2}\alpha_y\times 2t_1 \\
0&=&v_0\sin\theta-\frac{1}{2}2v_0\sin\theta \\
\end{eqnarray}
おかしな結果になったのは、もともと\(t_1\)を(3-24)式から求めているからです。
(3-24)式から得られた値を(3-24)式に戻せば、得られる結果は恒等式です。
\(t_2=2t_1\)を(3-24)式から得たのであれば、それはもう一つの式(ここでは(3-23)式)に代入して条件を求めなければなりません。
注) 等加速度運動の対称性
等加速度運動の対称性は例題のような設定ではよく使われます。
軌跡が放物線になり、このため、最高点を通る鉛直線に対して左右が対象になります。
つまり、点\(O\)から最高点までの時間と、最高点から点\(A\)までの時間は等しいです。
点\(O\)での電子の速度の\(y\)方向成分は、点\(B\)での速度の\(y\)方向成分と大きさが同じで向きが逆です。
本問では、電子の速度の\(x\)方向成分は変化しませんから、点\(O\)での電子の速さは点\(A\)での速さに等しいです。
いずれも、直観的にうなづける内容ですが、これらの知識を用いることで解答が容易になる場合があることを知っておきましょう。
⑦ 電子が\(y\)方向に\(y=0\)から\(y=h\)、そして再び\(y=0\)になるまでの時間と、\(x\)方向に\(l\) 進む時間が等しいという条件を考えます。
⑥で考察した\(2t_1\)が、まさに、電子が\(y\)方向に\(y=0\)から\(y=h\)、そして再び\(y=0\)になるまでの時間です。
\(x\)方向に\(l\)進む時間を\(t_2'\)として、これを求めるには、(3-23)式を用いて、
\begin{eqnarray} l&=&v_0\cos\theta t_2' \tag{3-36} \\
t_2'&=&\frac{l}{v_0\cos\theta} \tag{3-37} \\
条件は、2t_1&=&t_2'ですから、
-2\frac{v_0\sin\theta}{\alpha_y}&=&\frac{l}{v_0\cos\theta} \\
2\frac{mv_0\sin\theta}{eE}&=&\frac{l}{v_0\cos\theta} \\
eEl&=&2mv_0^2\sin\theta\cos\theta \tag{3-38}
\end{eqnarray}
(3-34)式と同じ式が得られました。
⑧ (3-23)(3-24)式から\(t\)を消去し、\(y\)を\(x\)の関数として表したとき、(\(l\)、\(0\))を通る条件として求めることもできますが、前の⑥⑦に比べて計算が多少煩雑になります。
Ⅳ.磁場、電磁力、電磁誘導
ここでは、磁場に関連した公式を扱います。
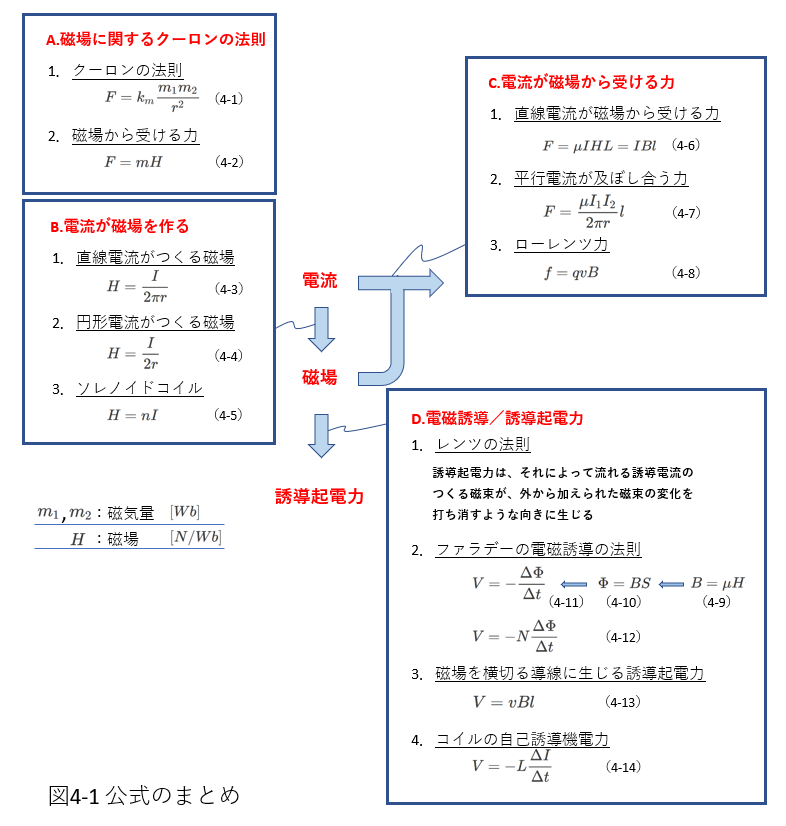
図4-1に磁場に関連した公式をまとめました。
公式を4つのグループに分けています。
グループAの磁場に関するクーロンの法則を表す(4-1)式は、2つの点電荷にはたらく静電気力の大きさを示すクーロンの法則と式の形が同じです。
後者のクーロンの法則における電気量が、前者では磁気量に置き換えられています。
万有引力の式とも同じ形ですね。
グループBは、電流が磁場を作ることに関連した式です。
この3つの式は確実に覚えましょう。
電流はその周囲に磁場をつくります。
ここで、「円形電流がつくる磁場」の(4-4)式 \(H=\frac{I}{2r}\)は円の中心での磁場の強さであることに注意しましょう。
円の中心から外れた位置での磁場の強さは(4-4)式とは異なります。
一方、「ソレノイドコイル」の(4-5)式の\(H=nI\)は、コイルの内部に形成される磁場で、コイルの軸に平行で、コイル内では一様な磁場です。
また、電流は磁場から力を受けます。
(電流と磁場の関係が、電荷と電場の関係に似ています。
・電荷が電場をつくります。
・そして、電荷は電場から力を受けます。
・電荷は自分がつくる電場からは力を受けません。)
電流が磁場から受ける力に関係する式をグループCにまとめています。
「直線電流が磁場から受ける力」の(4-6)式\(F=IBl\)は、教科書では証明なしで与えられています。
そして、「ローレンツ力」を表す(4-8)式\(f=qvB\)は、(4-6)式の\(F=IBl\)式から導出されています。
「平行電流が及ぼし合う力」の(4-7)式は、式の上では磁場とは無関係のように見えますが、電流\(I_1\)が\(I_2\)の位置につくる磁場から電流\(I_2\)が力を受けます。
したがって、(4-3)式から磁場\(H=\frac{I_1}{2\pi r}\)、そして、磁束密度\(B=\mu H\)を求め、(4-6)式\(F=I_2Bl\)を用いれば(4-7)式\(F=\frac{\mu I_1I_2}{2\pi r}l\)が得られます。
グループDは、「電磁誘導/誘導起電力」に関する4つの式を掲げています。
「レンツの法則」は、電磁誘導によりコイルに流れる電流の向きを考えるのに非常に強力な法則です。
「ファラデーの電磁誘導の法則」は、誘導起電力の基本的な式ですから十分に理解しましょう。
「磁場を横切る導線に生じる誘導起電力」の(4-13)式\(V=vBl\)は、(4-11)式\(V=-\frac{\Delta\Phi}{\Delta t}\)から導くことができます。
また、これとは別に、ローレンツ力の(4-8)式\(f=qvB\)から求めることもできます。
これらの導出過程は(教科書にも説明されていますが)、そのまま試験に出題されることもあるので、ここでも説明します
「.コイルの自己誘導起電力」については、(4-12)式\(V=-N\frac{\Delta\Phi}{\Delta t}\)を用いれば、コイルに流れる電流を\(I\)として誘導起電力\(V\)が\(-\frac{\Delta I}{\Delta t}\)に比例することが導かれます。
そして、その比例定数が自己インダクタンスを表します。
では、(4-13)式\(V=vBl\)を導出します。
最初に、ファラデーの法則から導きます。
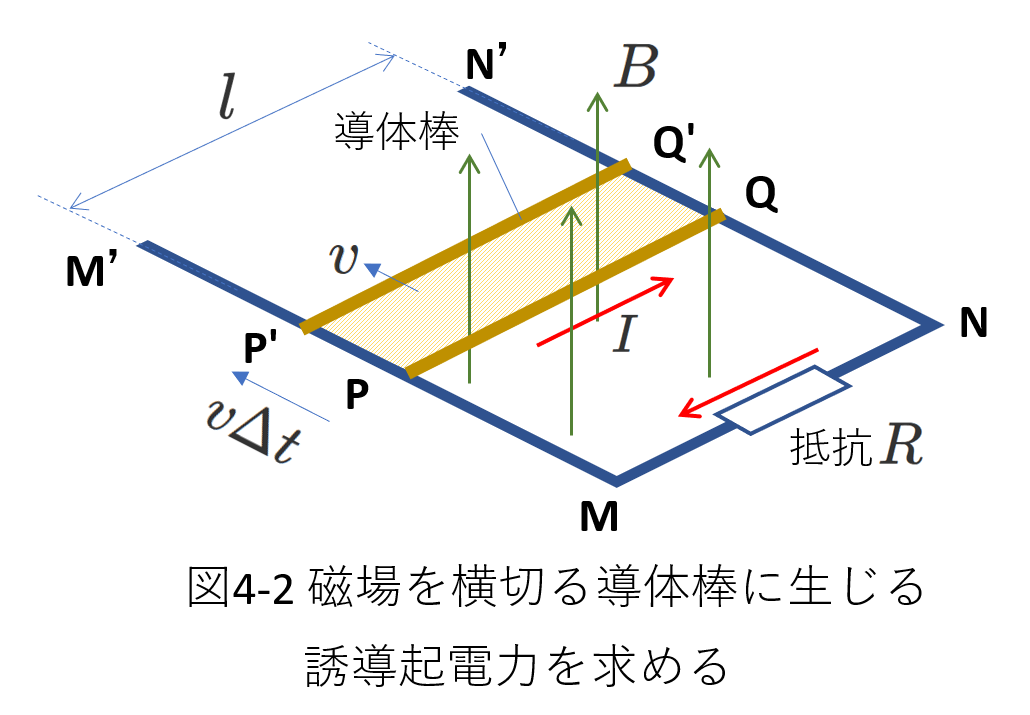
図4-2では、導体棒\(PQ\)が磁束密度\(B\)に垂直な方向に速さ\(v\)で運動しているとき、\(PQ\)に生じる誘導起電力を求めるわけですが、\(PQ\)が横切った磁束を明確にするために、\(PQ\)と共にコイルを形成するコの字形の導線\(M'MNN'\)を追加して考えます。
\(\Delta t\)の時間の間に\(PQ\)が\(P'Q'\)に移動するとき、\(PQ\)が通過する面積は\(lv\Delta t\)、したがって、横切る磁束は、\(Blv\Delta t\)です。
この分だけ、コイル\(PQNM\)を貫く磁束が増えるわけですから、磁束の変化量は\(\Delta\Phi=Blv\Delta t\)です。
ファラデーの法則から、誘導起電力の大きさ\(V\)は、
\begin{eqnarray} V&=&|-\frac{\Delta\Phi}{\Delta t}| \\
&=&\frac{Blv\Delta t}{\Delta t}
&=&vBl \tag{4-15}
\end{eqnarray}
そして、流れる電流の向きは、レンツの法則から、図4-2で\(PQ\)が図の向きに移動したとき、コイル\(PQNM\)を貫く磁束は増えるわけですから、それを打ち消すように、磁束を減少させる向きに電流は流れます。
それが、図の\(I\)の向きになります。
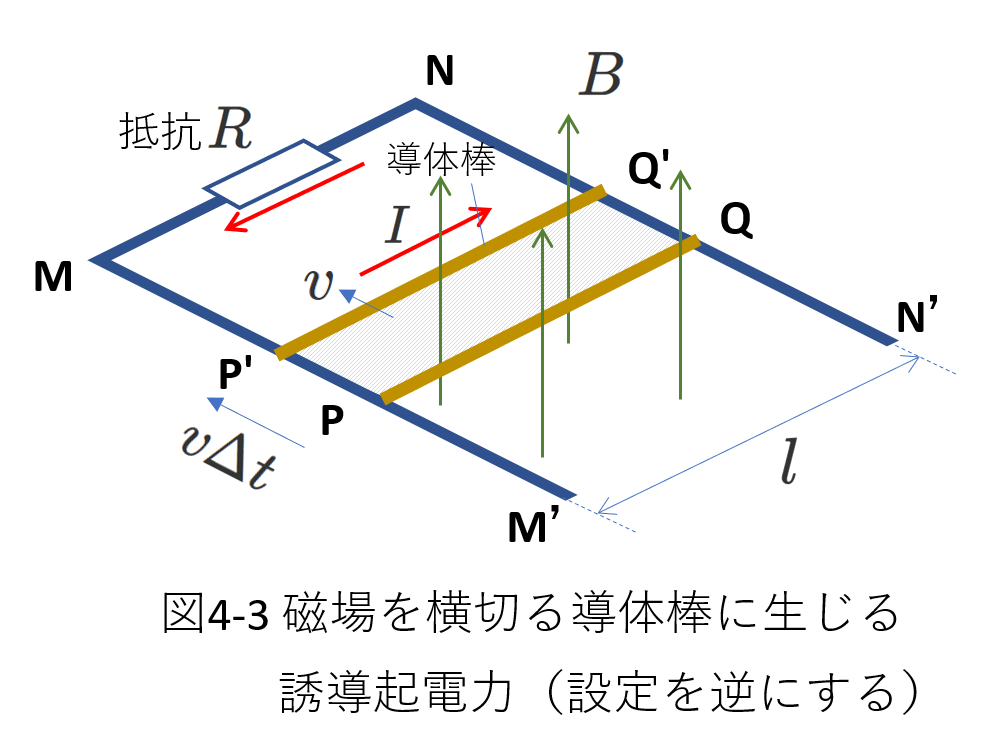
\(PQ\)をその一部とするコイルを考える場合、図4-3のようにコイルを形成するコの字形の導線\(M'MNN'\)を\(PQ\)の図4-2とは反対側に考えることができます。
図4-2では、導体棒の右側にコイルが形成され、図4-3では、導体棒の左側にコイルが形成されています。
導体棒\(PQ\)の誘導起電力を考えるわけですから、図4-2でも図4-3のモデルでも同じ結果になるはずです。
図4-3でも、\(PQ\)が横切る磁束は、\(Blv\Delta t\)です。
ただし、この図の場合には、コイル\(PQNM\)を貫く磁束は減少します。
したがって、
ファラデーの法則から、誘導起電力の大きさ\(V\)は、
\begin{eqnarray} V&=&|-\frac{\Delta\Phi}{\Delta t}| \\
&=&\frac{Blv\Delta t}{\Delta t}
&=&vBl
\end{eqnarray}
となり、(4-15)式と同じ結果になります。
そして、流れる電流の向きは、レンツの法則から、図4-3で\(PQ\)が図の向き(図4-2と同じ向き)に移動したとき、コイル\(PQNM\)を貫く磁束は減るわけですから、それを打ち消すように、磁束を増加させる向きに電流は流れます。
それが、図4-3の\(I\)の向きになります。
図4-2と図4-3ではコイルを流れる電流の向きは逆(図4-2では右回り、図4-3では左回り)ですが、導体棒\(PQ\)を流れる電流の向きは同じです。
つまり、図4-2で考えても、図4-3で考えても、導体棒\(PQ\)に生じる誘導起電力は同じ向きとなります。
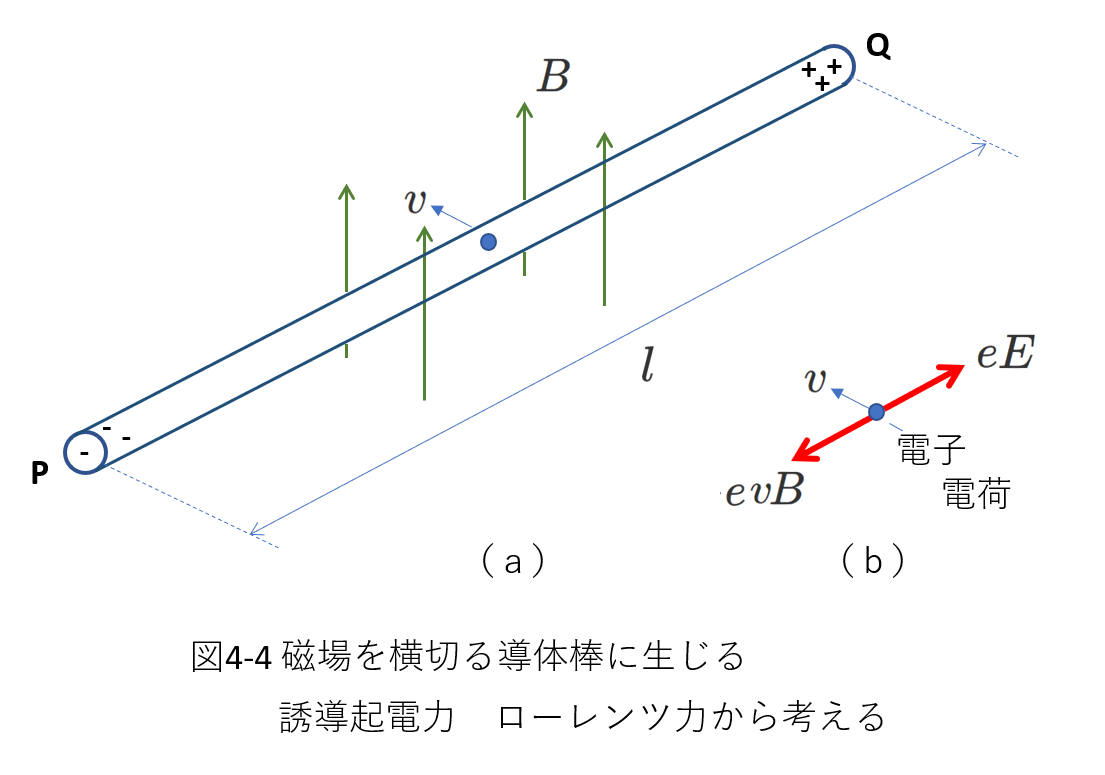
次に、ローレンツ力\(f=qvB\)を使って、(4-13)式\(V=vBl\)を導出します。
これを図4-4に示します。
導体棒\(PQ\)が図の向き(図4-2、図4-3と同じ向き)に速さ\(v\)で移動するとき、導体棒\(PQ\)の中の自由電子(電気量\(-e\))も同じ速さ\(v\)で移動することになり、ローレンツ力\(-evB\)がはたらきます。
この結果、電子は\(P\)側に移動し、\(P\)側が負に帯電し、電子が減った\(Q\)側が正に帯電します。
しかし、\(PQ\)の中心にあった電子が\(P\)まで移動するわけではありません。
\(PQ\)にある電子すべてが同じ力を受けて、電子全体がそろって\(P\)側にほんのわずか移動します。
その結果\(P\)の端に電子が、\(Q\)の端では電子が減少して正の電荷が現れることになります。
さて、これらの電荷により、\(PQ\)に電場が作られます。
この電場は、電子が\(P\)側に動くのを押さえる向きに生じます。
つまり、このとき、電子が受けるローレンツ力と電場から受ける力がつり合います。
つり合いの式は、
\begin{equation} eE=evB \tag{4-16} \end{equation}
\(PQ\)の長さは\(l\)ですから、誘導起電力\(V\)と\(E\)との関係は、
\begin{equation} E=\frac{V}{l} \tag{4-17} \end{equation}
これを(4-16)式に代入すると、
\begin{eqnarray} e\frac{V}{l}&=&evB \\
V&=&vBl \tag{4-18}
\end{eqnarray}
ローレンツ力から考察することでも誘導起電力の式\(V=vBl\)が導かれました。
ここで、電荷が移動したことにより発生する電場を\(E\)と仮定して問題を解くという電磁気に独特な考え方を覚えておきましょう。 つまり、
導体棒が運動を開始してから、どのぐらいの量の電気量がどのように移動するかについてまったく議論することなく、ただ最終的な状態を想定することで考察を進めることができるわけです。
とてもスマートな思考ですね。
この考え方は、このあとの図4-5~図4-8に関連した問題を解くときにも用います。
さて、図4-1に掲げた公式を使って解く問題には、通常次の要素が含まれます。
力\(F\)
速さ\(v\)
誘導起電力\(V\)
磁束密度\(B\)
電流\(I\)
それぞれの要素間の関係は図4-1に掲げた公式で表されます。
図4-1にない関係式は、誘導起電力\(V\)と電流\(I\)との関係を表すオームの法則\(I=\frac{V}{R}\)です。
(ここで\(R\)は回路の抵抗です。)
例題1
上の5個の要素の現れ方を、次の問題で見ていきましょう。
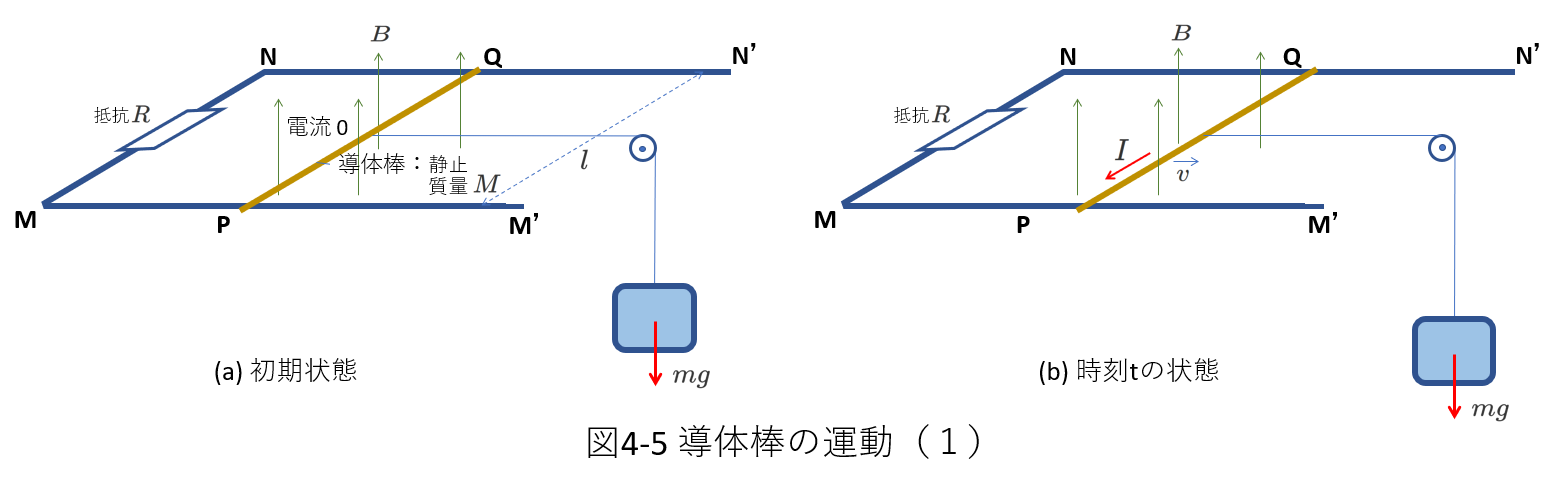
図4-5(a)に示すように、間隔\(l\)で2本の導線が水平面上に平行に置かれています。
その一端は抵抗\(R\)を介して導線で結ばれています。
また、2本の導線のレール上に導体棒\(PQ\)が導線に垂直に接触して置かれていて、その導線の上を自由に動けるようになっています。
導体棒\(PQ\)と導線の間に摩擦はありません。
導体棒\(PQ\)が導線に対して、移動中に傾くことはないものとします。
また、鉛直上向きに磁束密度\(B\)の一様な磁場があります。
導体棒は、滑車を介して図のように質量\(m\)のおもりに糸でつながれています。
時刻\(t=0\)で固定していたおもりを放します。
その後の導体棒\(PQ\)の運動を調べるために、導体棒の運動方程式を立ててみます。
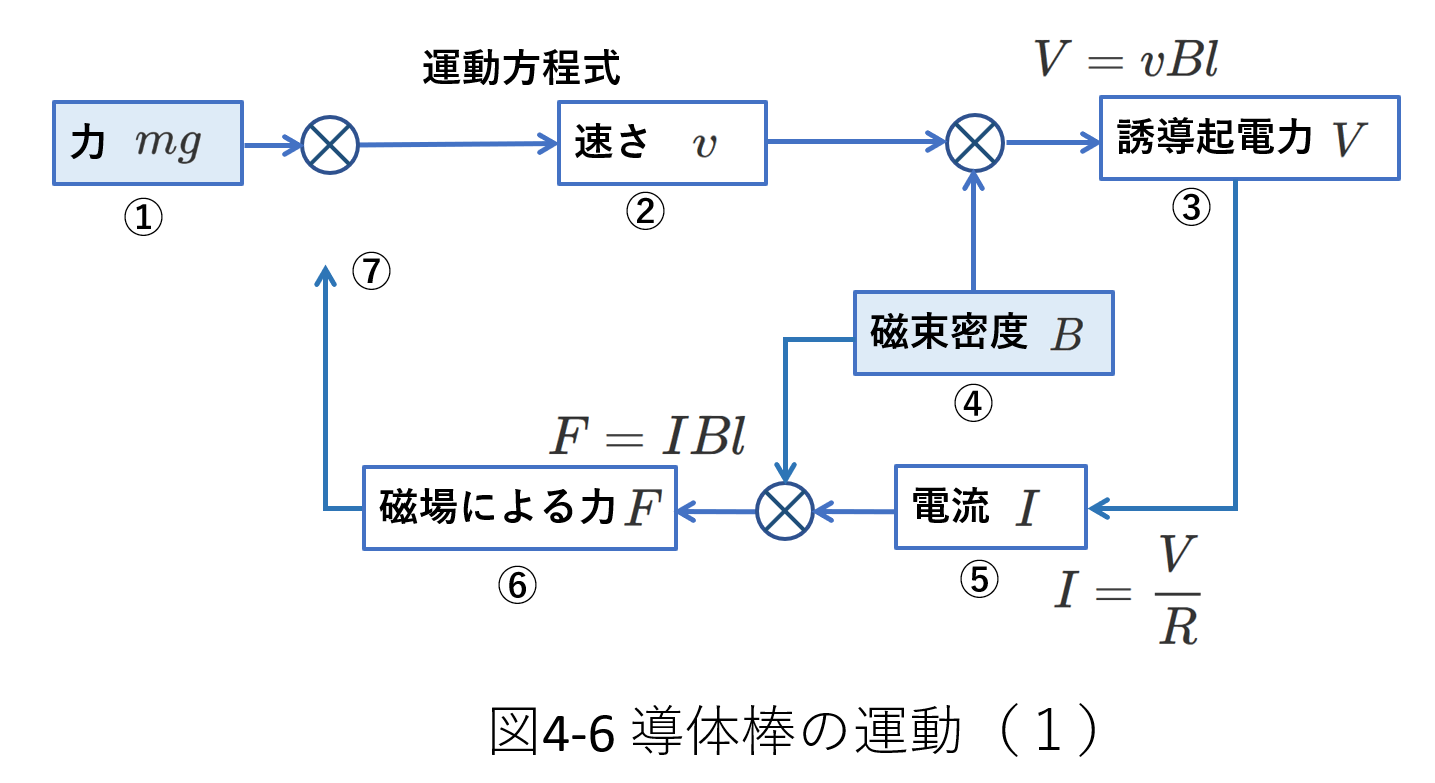
上であげた5つの要素の変化を追うために、図4-6を用意しました。
図に付した①~⑦の順番で考えます。
①\(t=0\)では、導体棒\(PQ\)にはたらく力は重力\(mg\)だけです。
\(PQ\)に電流は流れていないので、導体棒\(PQ\)は磁場から力を受けません。
したがって、導体棒\(PQ\)の質量を\(M\)、その加速度を\(a\)とすれば、図の右向きを正として、\(t=0\)の瞬間の運動方程式は、
\begin{equation} Ma=mg \tag{4-19} \end{equation}
②(4-19)式から導体棒\(PQ\)は右向きに動き出します。(以下図4-5(b)を参照)
ただし、(4-19)式は\(t=0\)の瞬間しか成り立ちません。
仮に、①の考察から、時刻\(t\)での導体棒\(PQ\)の速さ\(v\)がわかったとします。
③④すると、速さ\(v\)と磁束密度\(B\)から、導体棒\(PQ\)に生じる誘導起電力\(V\)が求められます。
⑤閉回路\(PQNM\)の抵抗\(R\)と起電力\(V\)から導体棒\(PQ\)に流れる電流\(I\)の強さと向きがわかります。
(電流は\(Q\to P\)の向きに流れますが、\(P\to M\to N\to Q\)を流れる電流は、\(PQ\)の位置に磁場をつくります。
この磁場まで考えると問題が複雑になりますから、通常、問題文中にこれらの磁場は無視して良いという説明がされます。
ここでも無視することにします。)
⑥⑦この電流\(I\)は磁場(磁束密度\(B\))から力\(F=IBl\)を受けます。
つまり、導体棒には、重力\(mg\)と磁場からの力\(IBl\)がはたらくことになるので、(4-19)式を書き改めてから、
再び、①~⑦の考察を進めるのですが、・・・これは無理があります。
そこで、普通はある瞬間、時刻\(t\)に成立する式を立てて考察します。
このとき、\(F、v、B、V、I\)の5つの要素全部を仮定することはしないで、普通は2つの要素、導体棒の速さ\(v\)、そこを流れる電流\(I\)を仮定します。
この問題では、磁束密度\(B\)は与えられているので、速さ\(v\)、電流\(I\)を使って磁場から受ける力\(F\)も誘導起電力\(V\)も表すことができます。
後でわかりますが、\(v\)は\(I\)を用いて、(あるいは\(I\)は\(v\)を用いて)表すことができます。
しかし、一度\(v\)と\(I\)を用いて式を立て、そののちにどちらか一つの変数の式に変形するほうが考察が容易です。
図4-6からもわかりますが、速さ\(v\)も電流\(I\)も時刻\(t\)の関数です。
言い換えれば、両者は時間の経過とともに変化します。
その変化を考察するのに、ある瞬間、時刻\(t\)での式を立てれば良いというところがこのような問題の面白いところです。
要するに、時刻\(t\)で成立する式というのは、任意の時刻においても成り立つ式ということですから、時間変化を考察することができるわけです。
では、図4-5(b)を参照して、時刻\(t\)に成立する運動方程式を立てます。
導体棒\(PQ\)の質量は\(M\)、時刻\(t\)での導体棒\(PQ\)の速さを\(v\)、そこを流れる電流を\(I\)と仮定します。
右向きを正とします。
導体棒は右に動きますから、電流の流れる向きは図4-5(b)に示すように\(Q \to P\)であることがわかります。
したがって、導体棒\(PQ\)が磁場から受ける力\(F\)は\(F=IBl\)で向きは左向きであることがわかります。
つまり、時刻\(t\)での運動方程式は、
\begin{equation} Ma=mg-IBl \tag{4-20} \end{equation}
となります。
この式から、\(a=\frac{mg-IBl}{M}\)としても、加速度\(a\)を求めたことにはなりません。
なぜなら、\(I\)は時間の関数であり、\(I\)がどう変化するかがわかっていないからです。
つまり、(4-20)式は\(a\)と\(I\)の2つの未知数を抱えています。
そこで、もう少し考察を進めて、\(I\)を\(v\)で表してみます。
\begin{eqnarray} V=vBl \tag{4-21} \\
ですから、I&=&\frac{V}{R} \tag{4-22} \\
&=&\frac{vBl}{R}
\end{eqnarray}
これより、運動方程式(4-20)式は、
\begin{equation} Ma=mg-\frac{vB^2l^2}{R} \tag{4-23} \end{equation}
となります。
この式から、\(a=\frac{mg}{M}-\frac{vB^2l^2}{MR}\)としても、加速度\(a\)を求めたことにはなりません。
\(v\)も時間の関数だからです。
それでは、(4-20)式を(4-23)式に変形したことは無駄かというと、そうではありません。
次のもうひとつの関係式があるからです。
\begin{equation} a=\frac{dv}{dt} \tag{4-24} \end{equation}
これを(4-23)式に代入すると、
\begin{eqnarray} M\frac{dv}{dt}=mg-\frac{vB^2l^2}{R} \\
M\frac{dv}{dt}+\frac{B^2l^2}{R}v-mg=0 \tag{4-25} \\
\end{eqnarray}
となり、結局\(v\)の1階の微分方程式が得られました。
これを解けば、\(v\) が時刻\(t\) の関数として求められます。
言い換えれば、\(v\) の時刻依存性がわかります。
しかし、(4-25)式を解くのは高校の学習の範囲を超えます。
のちほど、解いてみますが、ここでは(4-25)式を吟味することを考えます。
(4-25)式よりも、(4-23)式のほうが式の意味を捉えやすいので(4-23)式で考えることにします。
\begin{equation} Ma=mg-\frac{B^2l^2}{R}v \tag{4-23} \end{equation}
この式で変数は\(v\)と\(a\)で、そのほかは定数です。
変数が取り得る範囲に\(0\)が含まれていれば、その変数に\(0\)を入れて、式の意味を考えると良いです。
まず(4-23)式で\(v=0\)とすれば、
\begin{eqnarray} Ma=mg \tag{4-26} \\
a=\frac{m}{M}g \tag{4-27} \end{eqnarray}
\(v=0\)は、時刻\(t=0\)での導体棒\(PQ\)の速さです。
したがって、(4-26)式は\(t=0\)での運動方程式です。
(4-19)式と一致していますね。
時刻\(t\)のときの運動方程式として立式した(4-23)式ですが。\(t=0\)のときにも成り立ちます。
この変数に\(0\)を入れるという方法は、答えが正しいかどうかを検証することにも使えます
例えば、計算ミス、または、重力\(mg\)を見落として、運動方程式を
\begin{equation} Ma=-\frac{vB^2l^2}{R} \tag{4-28} \end{equation}
と立式したとします。
この式の右辺に\(v=0\)を代入すると、\(a=0\)となります。
これでは、導体棒\(PQ\)は動きません。
実際の運動と矛盾しますから、(4-28)式は誤りであるとわかります。、
(4-27)式は\(t=0\)での加速度です。
これにより、\(PQ\)の速さは\(0\)から増加していきます。
(4-23)式で\(v\)が\(0\)から増えていくと、(4-23)式の右辺の\(v\)の係数は正ですから、加速度\(a\)は小さくなることがわかります。
ただし、小さくなっても\(\frac{B^2l^2}{R}v\)が\(mg\)を超えない間は加速度\(a\)は正のままですから、\(v\)はさらに増加します。
つまり、\(\frac{B^2l^2}{R}v\)は\(mg\)にどんどん近づき、最後に、\(\frac{B^2l^2}{R}v=mg\)となり、\(a=0\)となります。
このことは運動が等速度運動になったことを示します。
一定になったときの速さ\(v_s\)を求めるには、(4-23)式で\(a=0\)を代入します。
つまり、
\begin{eqnarray} 0&=&mg-\frac{B^2l^2}{R}v_s \tag{4-29} \\
v_s&=&\frac{mgR}{B^2l^2} \tag{4-30}
\end{eqnarray}
(4-29)式は重力\(mg\)と磁場から受ける力の合力が\(0\)、すなわち、ふたつの力がつりあっていることを表していることに注意してください。
単に\(v_s\)を求めるだけならば、運動方程式(4-23)式を立てる必要はなく、ふたつの力のつり合いの式を立てれば良いことになります。
さて、以上の考察から、時刻により\(v\)がどう変化するかを考えます。
つまり、\(v-t\)グラフを描いてみます。
グラフを描くのに参考にできるのは、
1.\(t=0\)で加速度(つまり\(v-t\)グラフの傾き)は\(\frac{m}{M}g\)
2.時間が経つにつれ、\(v-t\)グラフの傾きは小さくなり、最後に\(0\)となる
3.傾きが\(0\)となったところでの速さは、\(\frac{mgR}{B^2l^2}\)
これらのことから、図4-7のようなグラフが描けます。
このグラフで、時間が経つにつれて\(v-t\)グラフの傾きは小さくなり、最後に\(0\)となっていることを確認してください。
例題2
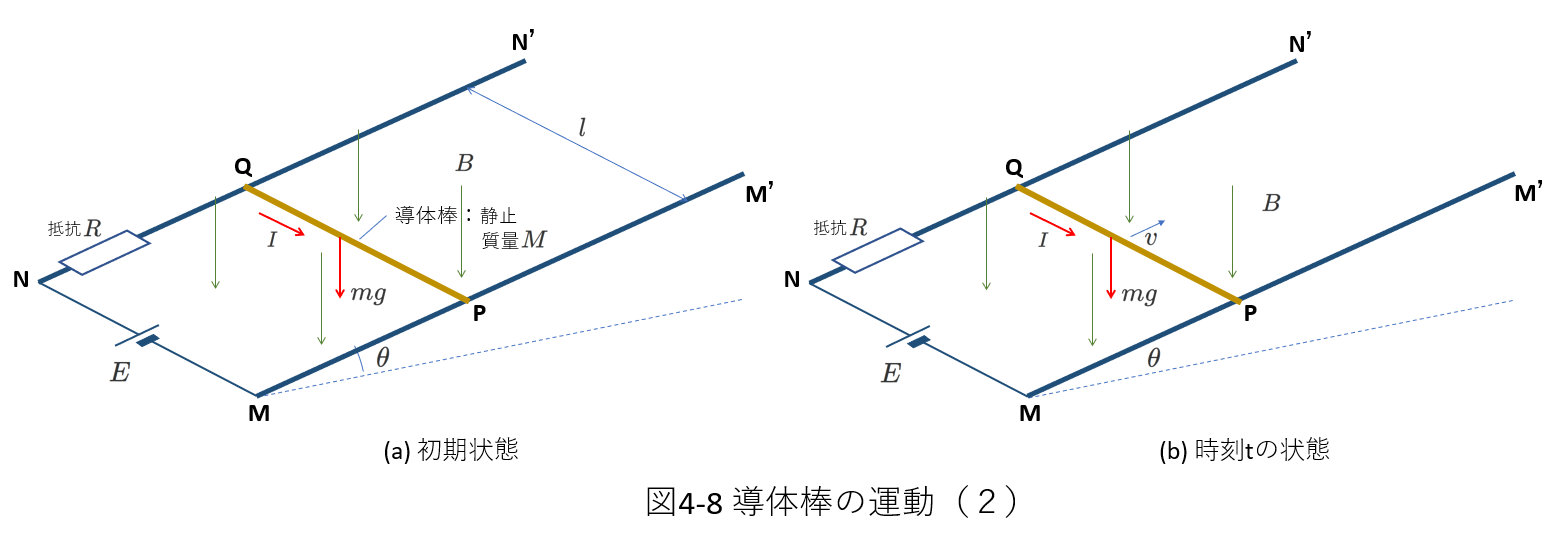
次の問題を図4-8に示します。
平行な2本の導線(レール)\(NN'\)と\(MM'\)が水平面からの角度が\(\theta\)となるように配置されています。
そしてこの上に2つの導線に対して垂直を保ったまま、2つの導線に接しながら自由に動くことができる導体の棒\(PQ\)が渡されています。
また、NMは起電力\(E\)の電池を介して導線で結ばれていて、\(NN'\)の図の位置には抵抗\(R\)が接続されています。
さて、導体棒\(QP\)を固定しておいて、時刻\(t=0\)で固定を外したところ、2つの導線上を上方に動き出しました。
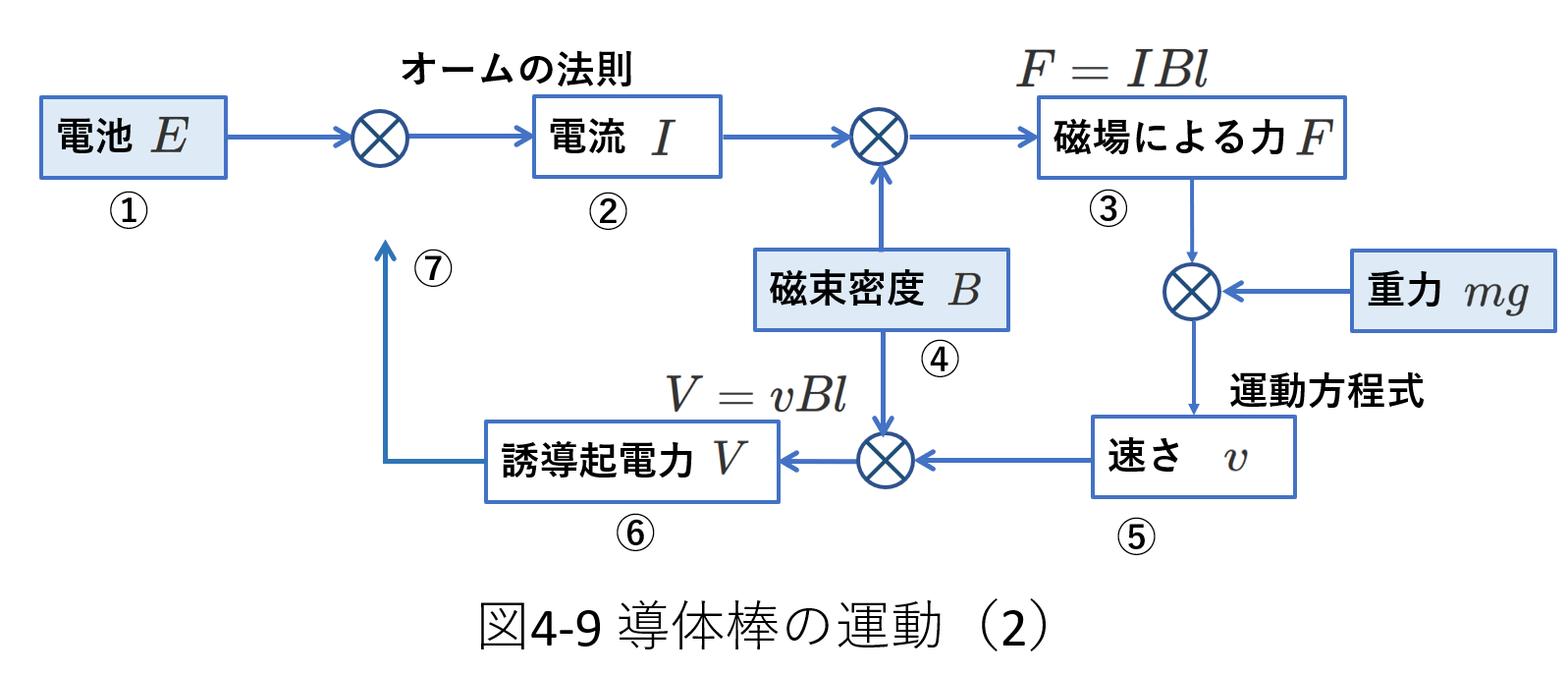
それ以後に怒ることを図4-9を参照しながら考えます。
図4-8の(a)は\(t=0\)のときの状態を表しています。
①②固定を外した直後の導体棒\(PQ\)の速さは\(0\)ですから、誘導起電力は生じていません。
したがって、\(PQ\)を流れる電流\(I\)は、オームの法則から\(I=\frac{E}{R}\)です。
③④磁束密度\(B\)の磁場が存在していますから、導体棒(を流れる電流)は磁場から\(F=IBl\)の力を受けます。
\(F\)の向きは、レールを登る向きです。
この力が十分に大きければ、重力に打ち勝ってレールを登り始めます。
導体棒\(PQ\)は磁場からの力以外に、重力\(mg\)、それから、\(NN'\)と\(MM'\)から面\(NMM'N'\)に垂直な方向に抗力\(T\)を受けます。
\(QP\)がふたつのレール上をすべるとすれば、抗力と、磁場からの力\(F\)と重力\(mg\)の抗力の方向の成分はつりあっているはずです。
そして、面\(NMM'N'\)に沿って、\(MM'\)に平行な向きの力の成分は、\(F\cos\theta\)、\(mg\sin\theta\)です。
⑤これらの力の成分を使って導体棒\(PQ\)に関して運動方程式を立てれば、その速さ\(v\)を求めることができます。
⑥\(PQ\)が磁場中を移動するので、\(PQ\)には誘導起電力\(V=vBl\cos\theta\)が発生します。
\(v\)と\(B\)の向きが垂直ではないことに注意してください。
\(QP\)がレールを登ると、閉回路\(MPQN\)を貫く磁束が増えるので、これを妨げる向きに誘導起電力が生じます。
これは、\(P\to Q\)へ電流を流す向きとなります。
⑦誘導起電力が発生すれば、\(PQ\)を流れる電流\(I\)は電池の起電力\(E\)と誘導起電力\(V\)から計算されることになります。
以上のように考えるとすごく複雑な問題だと感じますが、この問題でも、時刻\(t\)の瞬間について考察すると良いです。
そこで、時刻\(t\)で速さが\(v\)、電流が\(I\)として、運動方程式を立てます。
\(PQ\)の質量を\(M\)、加速度を\(a\)とします。
また、上る向きを正として、\(MM'\)の方向について運動方程式を立てます。
\begin{eqnarray} Ma&=&F\cos\theta-mg\sin\theta \\
&=&IBl\cos\theta-mg\sin\theta \tag{4-31}
\end{eqnarray}
次に\(I\)から時刻\(t\)での速さ\(v\)を求めますが、その前に誘導起電力は
\begin{eqnarray} V&=&vBl\cos\theta \tag{4-32} \\
オームの法則式から、 \\
I&=&\frac{E-V}{R} \tag{4-33} \\
&=&\frac{E-vBl\cos\theta}{R}
\end{eqnarray}
以上より、(4-31)式は、
\begin{eqnarray} Ma&=&IBl\cos\theta-mg\sin\theta \tag{4-31} \\
&=&\frac{E-vBl\cos\theta}{R}Bl\cos\theta-mg\sin\theta \\
&=&\frac{EBl\cos\theta-vB^2l^2\cos^2\theta}{R}-mg\sin\theta \\
&=&\left(\frac{EBl\cos\theta}{R}-mg\sin\theta\right)-\frac{B^2l^2\cos^2\theta}{R}v \tag{4-34}
\end{eqnarray}
ここで、最初の例題と同じように\(v=0\)を代入すると、
\begin{equation} Ma=\frac{EBl\cos\theta}{R}-mg\sin\theta \tag{4-35} \end{equation}
\(t=0\)で\(a\gt 0\)であれば\(PQ\)は上昇を始めますから、上昇する条件は、
\begin{equation} \frac{EBl\cos\theta}{R}-mg\sin\theta\gt 0 \tag{4-36} \end{equation}
運動方程式を立てる問題であれば、上のように考えるわけですが、単純に\(t=0\)で重力よりも、磁場から受ける力の\(MM'\)の方向の力が大きいと考えて、
\begin{equation} \frac{EBl\cos\theta}{R}\gt mg\sin\theta \tag{4-37} \end{equation}
のように式を立てることもできます。
(4-36)(4-37)式から、導体棒\(PQ\)を上昇させるための\(E\)の条件を求めることができます。
\begin{equation} E\gt\frac{mgR}{Bl}\tan\theta \tag{4-38} \end{equation}
(4-34)式の形は(4-23)式と同じですから、\(v\)の変化も(4-23)式と同じになります。
すなわち、時間が経つにつれて、\(v\)は大きくなりますが、\(v\)が大きくなると加速度\(a\)が減少しますから、\(v\)の増加割合は減少し、最終的に、一定の速さ\(v_s\)になります。
このとき、加速度\(a=0\)から、あるいは、このとき、重力と磁場から受ける力の\(MM'\)の方向の力がつりあっていることから、
\begin{equation} \frac{EBl\cos\theta-v_sB^2l^2\cos^2\theta}{R}=mg\sin\theta \tag{4-39} \end{equation}
ここから、\(v_s\)を求めることができます。
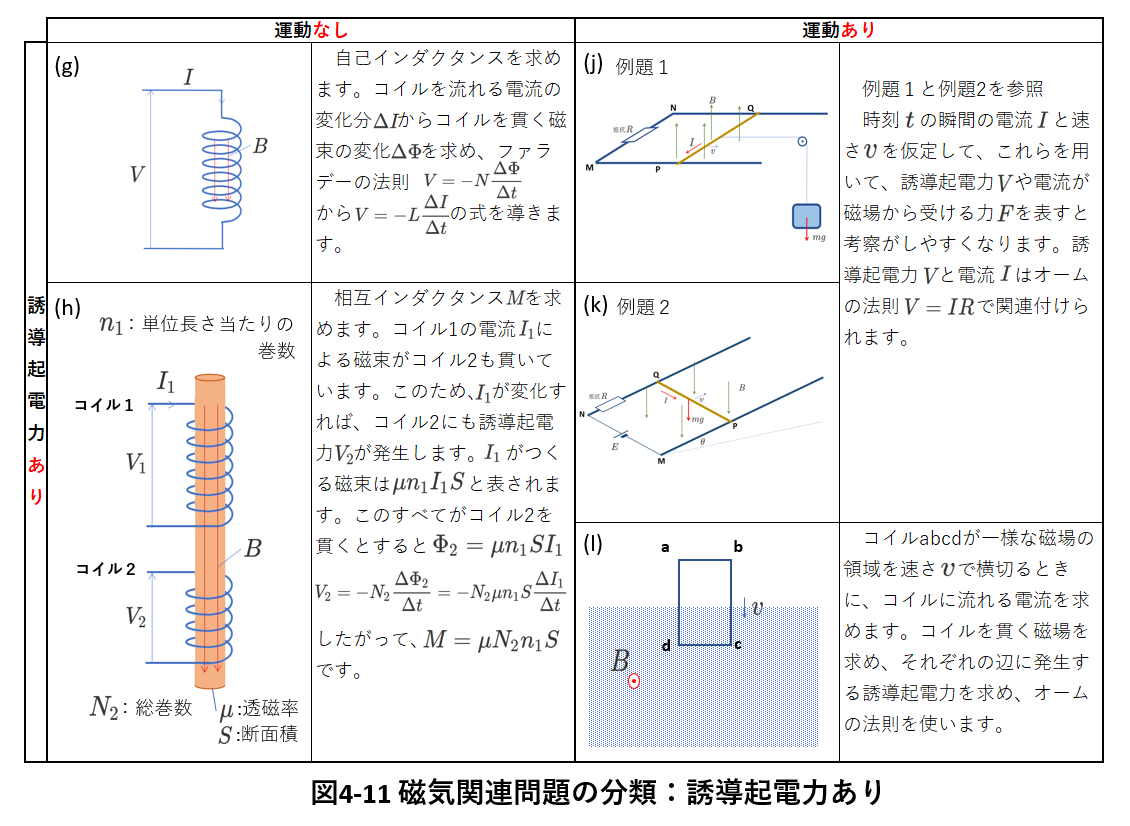
磁気の分野では、様々な問題が出題されるので、それらを分類して整理してみます。
分類の基準のひとつは、問題あるいは解法に誘導起電力が含まれているか否かです。
そして、もうひとつは、電荷あるいは導体の運動を考えるか否かです。
電流は電荷が動いていることを意味しますが、ここでは、電流は、「運動あり」に含めないことにします。
図4-10は、「誘導起電力なし」の問題を示しています。
左欄は「運動なし」、右欄は「運動あり」です。
左欄の「誘導起電力なし」「運動なし」のグループは、導線を流れる電流により発生する磁場の大きさや向き、さらに、その磁場により電流が流れる別の導線が磁場から受ける力を求める問題です。
たとえば、図4-10の(b)の平行電流が及ぼし合う力を求める問題などです。
この問題は教科書でも扱われている基本的な問題ですが、理解を試すために出題される可能性もあります。
次に、右欄の「誘導起電力なし」「運動あり」のグループは、磁場中での電荷の運動を扱う問題です。
教科書に載っている問題としては、図4-10の(f)のホール効果に関する問題がそれにあたります。
図4-11は、「誘導起電力あり」の問題を示しています。
左欄は「運動なし」、右欄は「運動あり」です。
左欄の「誘導起電力あり」「運動なし」の問題は、自己(相互)誘導起電力や自己(相互)インダクタンスを求める問題です。
これらも、導出過程が教科書等に載っていますが、導出過程が出題されることもあるので、その導出手順やその考え方は覚えておきましょう。
右欄は、「誘導起電力あり」「運動あり」のグループで、この章の図4-5や図4-8の問題がこのグループに属します。
最も複雑な問題とも言えますから、演習問題等で解法のコツを掴んでおきましょう。
では、最後に(4-25)式の微分方程式を解いてみます。
\begin{eqnarray} M\frac{dv}{dt}+\frac{B^2l^2}{R}v-mg=0 \tag{4-25} \\
\frac{dv}{dt}&=&-\frac{B^2l^2}{MR}v+\frac{mg}{M} \tag{4-40} \\
&=&-\frac{B^2l^2}{MR}\left(v-\frac{mgR}{B^2l^2}\right) \\
&=&-A\left(v-v_s\right) \tag{4-41} \\
ここで、A&=&\frac{B^2l^2}{MR}、v_s=\frac{mgR}{B^2l^2}
\end{eqnarray}
この微分方程式の解は、
\begin{equation} \frac{dv}{dt}=-Av \tag{4-42} \end{equation}
の一般解を\(v_1\)、
\begin{equation} \frac{dv}{dt}=-A(v-v_s) \tag{4-43} \end{equation}
の特殊解を\(v_2\)として、\(v_1+v_2\)が求める解となります。
どうしてそれで良いかの説明は省きます。
\(v=v_1+v_2\)を(4-41)式に代入してみれば、\(v_1+v_2\)が解であることが確認できます。
(4-42)式を解きます。
\begin{eqnarray} \frac{dv}{dt}&=&-Av \\
\frac{1}{v}dv&=&-Adt \\
両辺をtで積分すると、C_1を積分定数として、 \\
\int\frac{1}{v}dv&=&-At+C_1 \\
ln|v|&=&-At+C_1 \\
v&=&e^{-At+C_1}=C_1'e^{-At} \tag{4-44} \\
ただし、C_1'=e^{C_1}
\end{eqnarray}
次に、(4-43)式の特殊解(つまり、とにかく(4-43)式を満たす解のひとつ)は、式の形から、\(v=v_s\)(つまり定数)であることがわかります。
したがって、
\begin{equation} v=C_1'e^{-At}+v_s \tag{4-45} \end{equation}
さて、初期条件から積分定数\(C_1'\)の値を求めます。
\(t=0\)で\(v=0\)ですから、これらを(4-45)式に代入して、\(C_1'=-v_s\)が得られます。
したがって、
\begin{eqnarray} v&=&-v_se^{-At}+v_s \\
&=&v_s\left(1-e^{-At}\right) \tag{4-46}
\end{eqnarray}
(4-46)式は、\(t=0\)で\(v=0\)、\(t\to +\infty\)で、\(v\to v_s\)です。
(4-46)式は、図4-7のグラフと一致することを確かめてください。
関連ページ
- コンデンサーを理解する
- コンデンサについて学んでおくべき内容のうち、コンデンサーの性質を説明しています。
- コイルを理解する
- 電磁気学で学んでおくべき内容を項目に分けて説明しています。